宇宙膨脹知多少


大爆炸與膨脹的宇宙

宇宙的膨脹是最偉大的科學發現之一。這種膨脹，連同物質的相互引力，推動了宇宙的演化，將其從熾熱均勻的狀態轉變為我們今天觀察到的寒冷和聚集狀態。它是現代宇宙學的基石，使大爆炸理論家喻戶曉。宇宙現時的膨脹率被稱為哈勃常數，以於1929年通過觀察附近星系的運動發現宇宙膨脹的天文學家埃德溫·哈勃（Edwin Hubble）的名字命名，在宇宙學中至關重要。

許多人錯誤地認為宇宙膨脹是一次大爆炸的結果。大爆炸導致物質從空間中的一個固定點四散飛出，如圖1所示。根據這種觀點，爆炸發生在原本空曠的空間中的獨特位置，這意味著我們需要相對靠近這個爆炸點（宇宙的中心）才能觀察到大多數星系都在「向外」移動，使得它們的光線受到多普勒紅移，就像救護車的警報器在遠離我們時頻率降低一樣。


圖1 對大爆炸的常見錯誤看法：發生了一次巨大的爆炸，物質從中心四散飛出，進入了原來虛無的太空。星系產生的光遭受多普勒紅移，而我們恰好住在爆炸中心附近。


然而，這樣的爆炸情景與宇宙學原理相矛盾，宇宙學原理是現代宇宙學理論的一個基本假設。該原理指出，宇宙在大尺度上是均勻的和各向同性的。換句話說，我們假設宇宙從任何位置和各個方向看起來都是一樣的。 如果這個假設不成立，就沒有理由相信我們做的宇宙學觀測真的有普遍性及代表性。此外，物質在固定的空間中高速離散的概念與廣義相對論相矛盾，廣義相對論指出時空和物質相互作用。靜態空間在廣義相對論中並不是一個穩定的解法[2]，這連愛因斯坦也感到驚訝。

與廣義相對論和宇宙學原理一致的觀點是，空間在星系之間均勻膨脹（見圖2）。從任何一個星系的角度來看，所有其他星系似乎都在向各個方向移動。此外，星系後退的視線速度與它與觀察者的距離成正比。


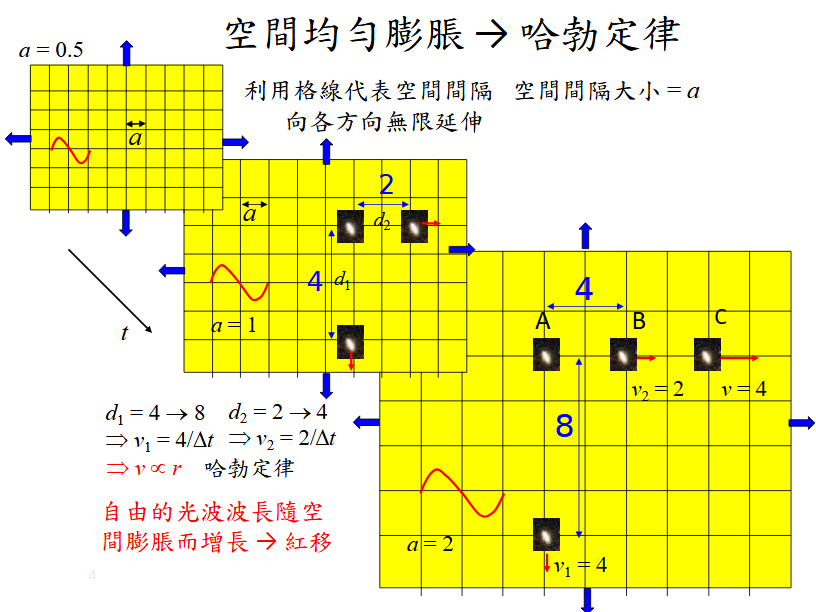
圖 2 宇宙的膨脹應該理解為遙遠星系之間的空間均勻膨脹。我們可以一個網格來說明這個空間的相對大小，網格寬度為 a，並且隨著時間的推移而增加。哈勃定律描述了這種空間的均勻膨脹。這種理解與宇宙學原理和廣義相對 論都是一致的。


讓我們考慮星系B和C，它們在時間t = t₀ 時分別位於距離星系A相距2和4個單位的位置。當時間t = t₀ +∆t時，由於空間的均勻膨脹，從A到星系B和C的距離都增加了一倍，成為4和8個單位。因此，從A的角度來看，星系B 和C似乎分別以 2/∆t 和4/∆t個單位的速度後退，這與它們的距離呈完美的比例關係。我們得出結論， v = Hd，其中H 是稱為哈勃參數的比例常數。這關係被稱為哈勃定律。在這個模型中，宇宙中的每個點都被認為是一個膨脹中心，網格向各個方向無限延伸，確保宇宙保持均勻和各向同性。

由於宇宙的膨脹，物質和能量的密度會隨著時間而降低。結果，宇宙從最初的熱和緻密狀態演變成我們今天觀察到的寒冷和彌散狀態。哈勃參數 H也隨時間而變化。宇宙學模型，例如暗能量冷暗物質 (ɅCDM)模型[3]， 可以預測H 如何變化並描述宇宙的膨脹歷史（見圖3），這可以通過觀測來檢驗。天文學家已使用各種方法測量現今宇宙的膨脹率，稱為哈勃常數 H₀[4]。


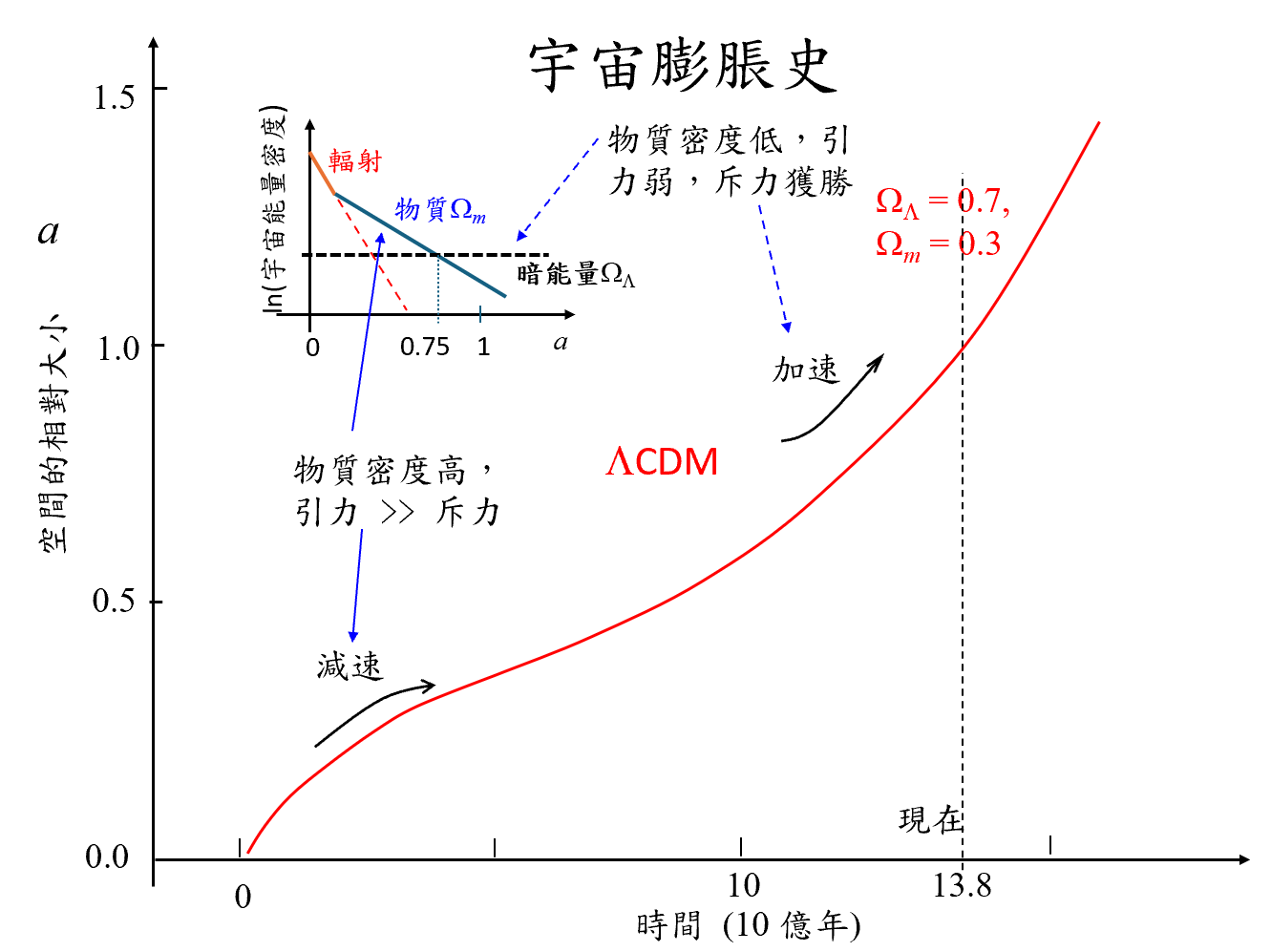
圖 3 根據CDM繪製的宇宙膨脹歷史草圖。隨著物質密度的下降，由於相互引力減弱，減弱的早期膨脹過渡到晚期加新速。


哈勃常數危機–標準宇宙學模型的挑戰

最近，不同的哈勃常數的測量值出現了顯著的差異[5]。這些測量可以 分為兩類：基於來自相對較近的天體（如超新星）的光的局域測量，以 及基於對宇宙微波背景的觀測及採用標準宇宙學模型得出的全域測量。 局域測量報告的值約為73 ± 1 km/s/Mpc，這意味著兩個相距1Mpc （約330萬光年）的星系以每秒73公里的速度彼此後退，但全域測量 更傾向於67 ± 0.5 km/s/Mpc。

局域測量使用哈勃定律直接決定哈勃常數， H₀ = v/d。雖然近鄰星體的沿視線速度v 可以通過其紅移來測量，但要確定其距離d則頗具挑戰性。 幸運的是，一些宇宙天體的本徵亮度是已知的或可以很容易地測量到 。這些被稱為標準燭光。例如，造父變星的亮度變化週期和本徵亮度 之間存在緊密的相關性，前者相對容易測量。一旦知道了物體的本徵 亮度，與它的視亮度的比較就會告訴我們它的距離，因為後者隨著距 離的平方而下降。天文學家使用近鄰的標準燭光，例如造父變星，通 過多種方法進行交叉檢查其距離，因此更可靠，來校準距離較遠的標 準燭光，例如1A型超新星[6]。

這種局域測量並不依賴於特定的宇宙學模型。然而，距離測量可能會 出現系統誤差，特別是因為「標準燭光」是否真的是「標準」可能值 得商榷。

此外，測得的星體紅移未必完全是由於哈勃膨脹導致，因此不完全對應於 H₀d。任何宇宙天體都可能被其相鄰天體吸引，以致其運 動偏離哈勃膨脹（見圖4）。這種現象稱為本動運動。換句話說(參考圖2)， 我們不應該假設星系一直卡在網格上。由於它們受附近的天體影響，它們也 會相對於網格移動。除了哈勃膨脹之外，星系的本動運動vp 亦會影響其視線速度v = vp + H₀d。雖然 H₀d 始終為正數，但 vp 可以是正數或負數。


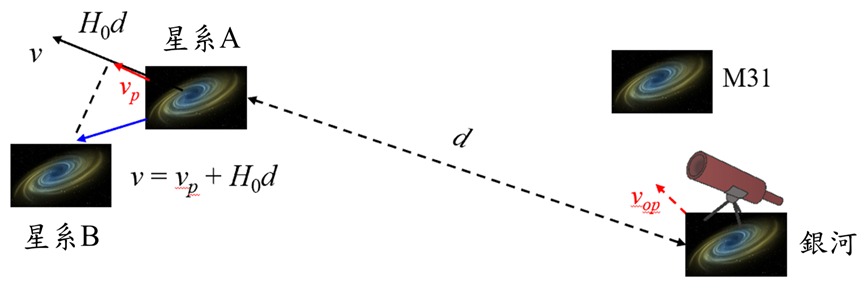
圖4 我們觀測到星系A與B的速度包含因它們相互作用引起的本動運動速度， vp。 銀河系的本動運動，例如由於我們的相鄰星系M31的吸引（紅色虛線箭頭表示） ，也會影響H₀ 的局域測量。


根據宇宙學原理，不同宇宙天體的本動運動方向和幅度應為隨機的， 因此當對許多天體進行平均時，它們對H₀ 的貢獻應該有效地相互抵消。然而，觀測結果也受到觀測者相對於 哈勃膨脹的本動運動的影響，觀測者的本動運動不會通過多次測量 的平均值來抵消，從而導致H₀測量值的系統誤差。

哈勃常數 (H₀) 的全域測量取決於從早期宇宙熱等離子體中的聲波得出的標準長度。 這種等離子體在宇宙最早大約400,000年的時間對光子不透明，在此 期間，宇宙的溫度高達約3000 K。當宇宙膨脹並冷卻到此溫度以下時 ，等離子體轉變為中性氫氣，類似於水蒸氣在100 °C時凝結成液體的 狀況。此時，從等離子體發射的光子就可以自由地穿過中性氣體，即 所謂的光子退耦。

這些光子今天仍然存在，但它們的波長已經隨著宇宙膨脹而拉長了約1100 倍 ，形成了宇宙微波背景（CMB）[7]。WMAP 和Planck等任務已經精確測量了全 天空CMB溫度分佈，提供了光子退耦時宇宙微波背景天空的快照（見圖5）。CMB 中看似隨機的溫度波動模式是由原始等離子體中激發的許多聲波的相互干涉產生 的。這些波動的詳細分析提供了有關宇宙的大量資訊，包括重要的宇宙學參數[8]。


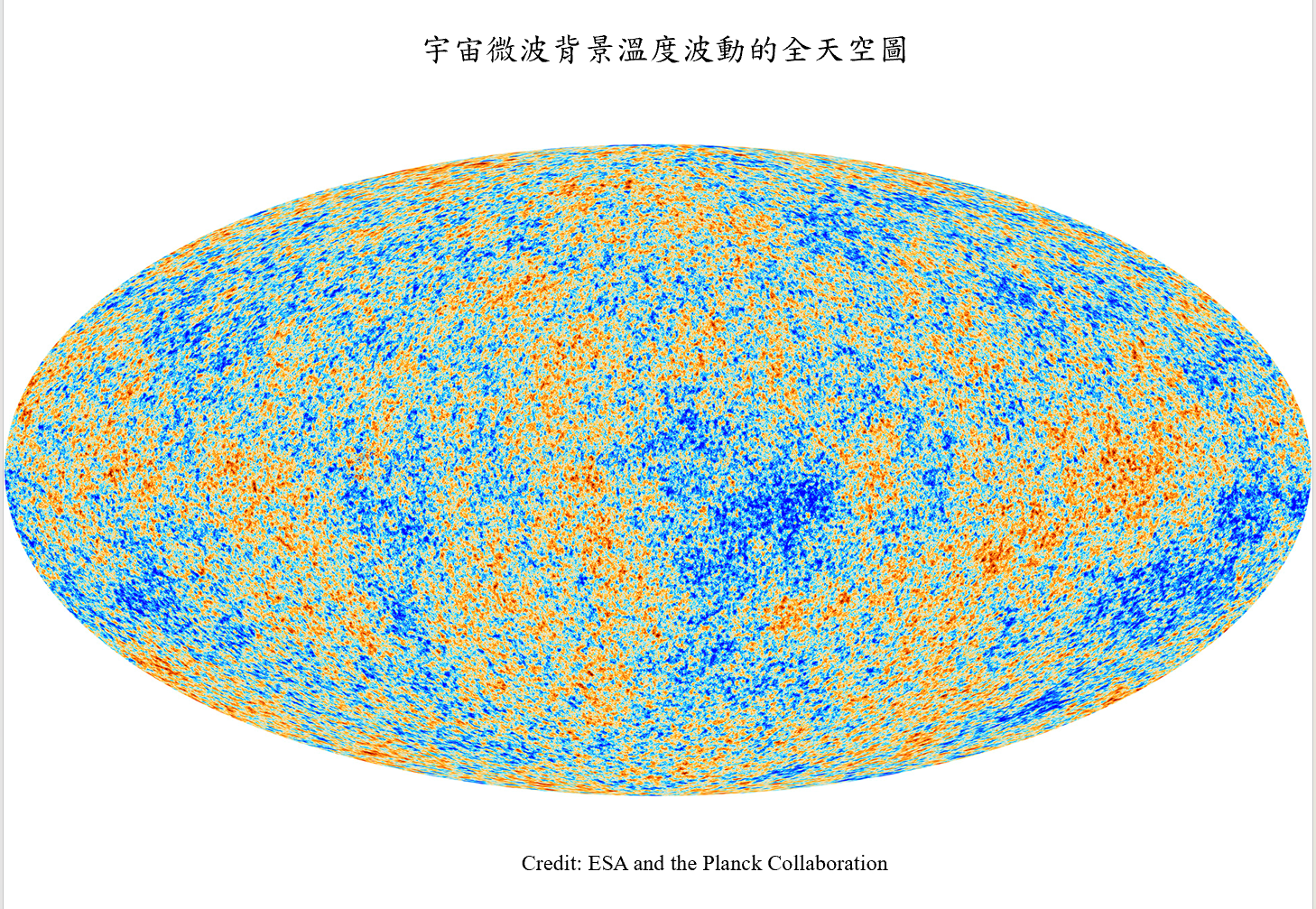
圖5 宇宙約380,000歲時全天空CMB溫度分佈快照。顏色表示略熱（紅色）到偏 冷（藍色），平均溫度為2.725 K，漲落約為 10⁻⁴ K。 圖片來源：ESA/Planck Collaboration。


這些聲波的基本振盪模式，類似於由兩端固定的琴弦產生的最簡單的駐波，在CMB圖上建立了大約1°的角度尺度 θ（見圖6）。在這個尺度上，溫度波動是顯著相關的。而這個 θ 角的基線是光子退耦表面到我們的距離 D，這取決於自光子退耦以來宇宙的膨脹歷史，因此受H₀影響，所以 H₀ 的數值與角度 θ密切相關。雖然 θ 可以通過CMB觀測進行高精度測量，但需要假設宇宙膨脹歷史模型來估算 H₀。因此， H₀的全域測量依賴於 ɅCDM的正確性。


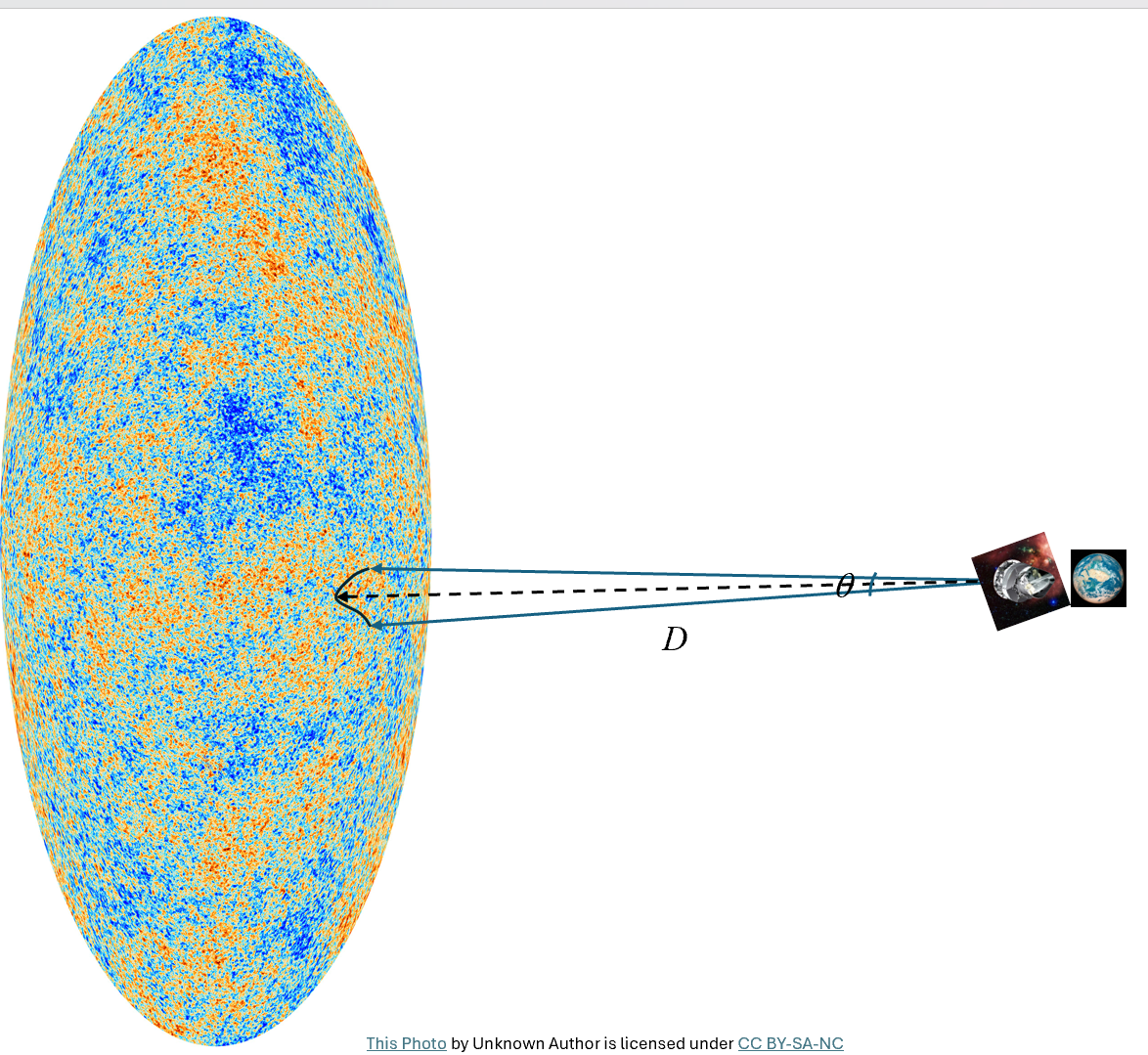
圖6 測量CMB溫度漲落與地球的相關角。光子退耦表面的聲波振盪在距離D上形成一個角度θ。


哈勃常數危機引起了極大的興奮和關注，因為它可能表明超越標準宇宙學模型 和粒子物理標準模型的新物理學的存在。例如，哈勃常數危機的一個可能解決 方案是引入以前未檢測到的輻射（非光子和中微子），稱為暗輻射。與 ɅCDM相比， 這會改變宇宙的膨脹歷史，並使CMB的哈勃常數測量值與局域 測量值保持一致。這種暗輻射的存在如果得到證實，將會是基礎物理的重要突破。

鑒於哈勃常數危機的重要性，研究人員亟需建立獨立可靠的(H₀) 測量方法，以檢查局域和全域測量值的異同。

揭開星系對的隱藏動態

香港中文大學物理系的團隊最近進行的一項研究提出測量哈勃常數的新方法[9]。 該團隊包括博士生章王政、楊碩博士，以及合作者廖世鴻博士（2015年中大博士， 現職於中國國家天文台）和中國科學院大學的胡慧傑博士。研究結果發表在《天體 物理學期刊快報》（The Astrophysical Journal Letters）上，詳細介紹了一種利用星系對相互運動以測量 H₀的新方法。

我們並非通過觀察單個星系的視運動來測量 H₀ ，而是關注星系對的相對運動。這些運動受到它們相互引力作用和宇宙膨脹的影響。 我們使用了稱為星系對速度的統計測量方法，以量化星系對之間的相對運動，為宇宙 的結構和演化提供了重要觀察工具。通過檢查星系對速度，我們可以推斷出有關宇宙 大尺度動力學的關鍵細節，包括哈勃常數。

我們使用了先進的計算機模擬，稱為宇宙學N體模擬，來比較不同宇宙膨脹 場景中的星系對速度。我們將這些模擬的結果與從星系巡天收集的觀測數據 進行了比較，結果表明，星系對速度可以用作 H₀的獨立和準確測量，為哈勃常數危機提供了新的視角。

新的、更可靠的哈勃常數測量方法

新方法側重於星系對 內 星系之間的相對速度，有效地消減了常見的偏差，包括觀察者相對於宇宙膨脹的本動運動所引入的誤差。如圖7所示，觀測到的星系A和B的速度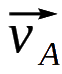， 和 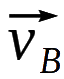，都包含觀察者本動運動的相同貢獻(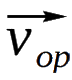)，但它們在星系A和B之間的相對速度中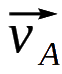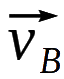， - 恰好被抵消了。其他共存於 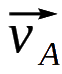和 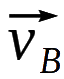的系統誤差，例如觀察者的儀器偏差，也在星系對速度中大幅抵消。 因此，該方法不僅可靠性更高，更能與現有的哈勃常數測量方法互補。


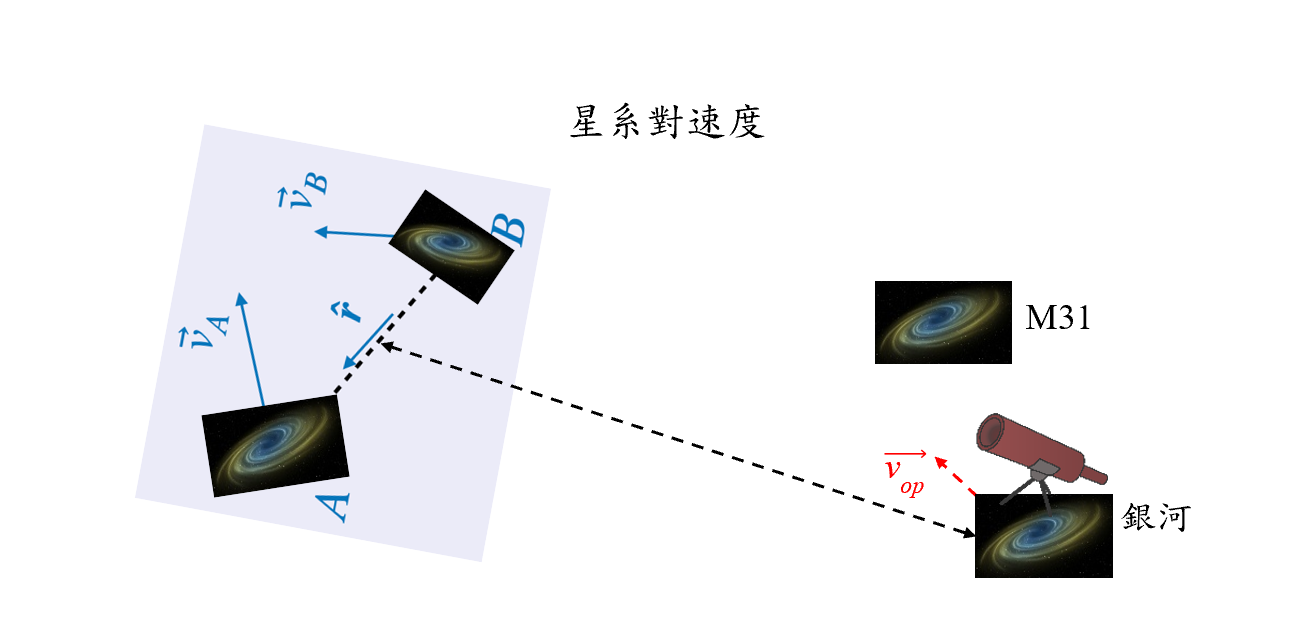
圖 7 星系對速度定義為兩個星系（例如星系A和B）沿其分離線投影的相對速度，如虛線所示。由於觀測到的星系A和B的速度 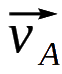（ 和 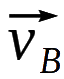），分別包含來自觀察者本動運動的相同貢獻，因此它們在相對速度中 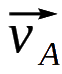- 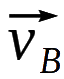抵消了。


新的測量將哈勃常數定為75.5 km/s/Mpc，誤差為1.4 km/s/Mpc，約為2%。 此結果與其他局域測量值一致。這再次證實了哈勃常數危機，進一步挑戰標準宇宙學模型。

此外，由於星系的運動受到它們相互引力作用的影響，因此星系對速度對物質密度也很敏感。使用新方法，我們獲得了宇宙學參數 Ωₘ的獨立測量值，該參數表示物質在宇宙總能量密度中的佔比。測量結果為 ❲Ωₘ❳ = 0.311，誤差小於0.03，即9%。這一結果與CMB和其他宇宙學數據的測量值非常吻合[8]。

即將進行的大規模巡天，例如LSST[10]，將以更高的精度測量更多的宇宙天體。因此，雖然我們的方法目前受到統計誤差的限制，但這些誤差在未來會顯著減少。使用我們的方法， H₀ 和 Ωₘ 的誤差可以分別降低到0.6%和2%。

星系對速度是宇宙學中一個很有用的工具。它不僅幫助我們測量哈勃常數和物質密度， 還能夠研究宇宙學中微子和其他假設的輕暗物質粒子的影響。這些輕宇宙粒子的運動速 度比冷暗物質快得多，使它們把冷暗物質形成的大尺度結構平滑化。這反過來又會影響 物質之間的引力相互作用，我們可以通過星系對速度測量來觀察這些變化。

通過進行宇宙學N體模擬，我們都可以研究這些輕宇宙粒子對星系對速度的影響。例如，我們利用這方法測量宇宙學中微子的特性[11]，並限制了輕惰性中微子[12]的存在，這個假設的粒子比熟悉的中微子[13]有更弱的相互作用。我們還在努力採用星系對速度來量度中微子質量，中微子質量非常小，即使是當今最好的實驗室實驗也無法直接測量它。

這就是宇宙學的美妙之處。宇宙進行了最大的實驗供我們觀察，即使是最微小的粒子，如中微子，也會留下它們的痕跡。有了更大、更先進的望遠鏡，我們可以觀測到更多的宇宙歷史，幾乎可以追溯到宇宙大爆炸。

理解宇宙的演化是人類偉大的追求，我們能夠為此作出即使是非常渺小的貢獻，亦與有榮焉。

參考資料

    1. E. Hubble, “A relation between distance and radial velocity among extra-galactic nebulae”. Proceedings of the National Academy of Sciences, 15, 168 (1929).
    2. See for example, S. Weinberg, “Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity” (Wiley, 1972).
    3. See for example, https://lambda.gsfc.nasa.gov/education/graphic_history/univ_evol.html; https://ned.ipac.caltech.edu/level5/Peebles1/Peeb2.html
    4. For recent reviews, see R. B. Tully, “The Hubble Constant: A Historical Review,” https://arxiv.org/abs/2305.11950 ; W. L. Freedman, B. F. Madore, “Progress in Direct Measurements of the Hubble Constant,” https://arxiv.org/abs/2309.05618.
    5. For a recent review, see E. D. Valentino et al., “The CosmoVerse White Paper: Addressing observational tensions in cosmology with systematics and fundamental physics,” https://doi.org/10.48550/arXiv.2504.01669
    6. A. G. Riess et al., Astrophysical Journal Letters, 934, L7 (2022) and references therein.
    7. An excellent review of CMB physics can be found in https://background.uchicago.edu/~whu/araa/node1.html.
    8. Planck Collaboration, “Planck 2018 results. I. Overview and the cosmological legacy of Planck,” Astronomy & Astrophysics, 641, A1 (2020).
    9. W. Zhang et al., “Measuring the Hubble Constant through the Galaxy Pairwise Peculiar Velocity,” Astrophysical Journal Letters, 978, L6 (2025).
    10. Legacy Survey of Space and Time https://rubinobservatory.org/for-scientists/rubin-101
    11. W. Zhang et al., “Measuring neutrino mass and asymmetry with matter pairwise velocities,” Monthly Notices of the Royal Astronomical Society, 529, 360 (2024).
    12. R. Hu et al., “Impact of light sterile neutrinos on cosmological large scale structure,” https://arxiv.org/abs/2501.16908.
    13. B. Dasgupta and J. Kopp, “Sterile Neutrinos”, Physics Reports, 928, 1 (2021).

    作者：
    香港中文大學物理系朱明中教授

    2025年6月