宇宙膨胀知多少


大爆炸与膨胀的宇宙

宇宙的膨胀是最伟大的科学发现之一。这种膨胀， 连同物质的相互引力，推动了宇宙的演化，将其从 炽热均匀的状态转变为我们今天观察到的寒冷和聚 集状态。它是现代宇宙学的基石，使大爆炸理论家 喻户晓。宇宙现时的膨胀率被称为哈勃常数，以于 1929年通过观察附近星系的运动发现宇宙膨胀的天 文学家埃德温·哈勃（Edwin Hubble）的名字命名 ，在宇宙学中至关重要。

许多人错误地认为宇宙膨胀是一次大爆炸的结果。大爆 炸导致物质从空间中的一个固定点四散飞出，如图1所 示。根据这种观点，爆炸发生在原本空旷的空间中的 独特位置，这意味着我们需要相对靠近这个爆炸点（宇宙 的中心）才能观察到大多数星系都在「向外」移动，使 得它们的光线受到多普勒红移，就像救护车的警报器在 远离我们时频率降低一样。


图1 对大爆炸的常见错误看法：发生了一次巨大的爆炸， 物质从中心四散飞出，进入了原来虚无的太空。星系产 生的光遭受多普勒红移，而我们恰好住在爆炸中心附近。


然而，这样的爆炸情景与宇宙学原理相矛盾，宇宙学原理是现 代宇宙学理论的一个基本假设。该原理指出，宇宙在大尺度上 是均匀的和各向同性的。换句话说，我们假设宇宙从任何位置 和各个方向看起来都是一样的。如果这个假设不成立，就没有 理由相信我们做的宇宙学观测真的有普遍性及代表性。此外， 物质在固定的空间中高速离散的概念与广义相对论相矛盾，广 义相对论指出时空和物质相互作用。静态空间在广义相对论中 并不是一个稳定的解法[2]，这连爱因斯坦也感到惊讶。

与广义相对论和宇宙学原理一致的观点是，空间在星系之间均匀膨胀 （见图2）。从任何一个星系的角度来看，所有其他星系似乎都在向各 个方向移动。此外，星系后退的视线速度与它与观察者的距离成正比。


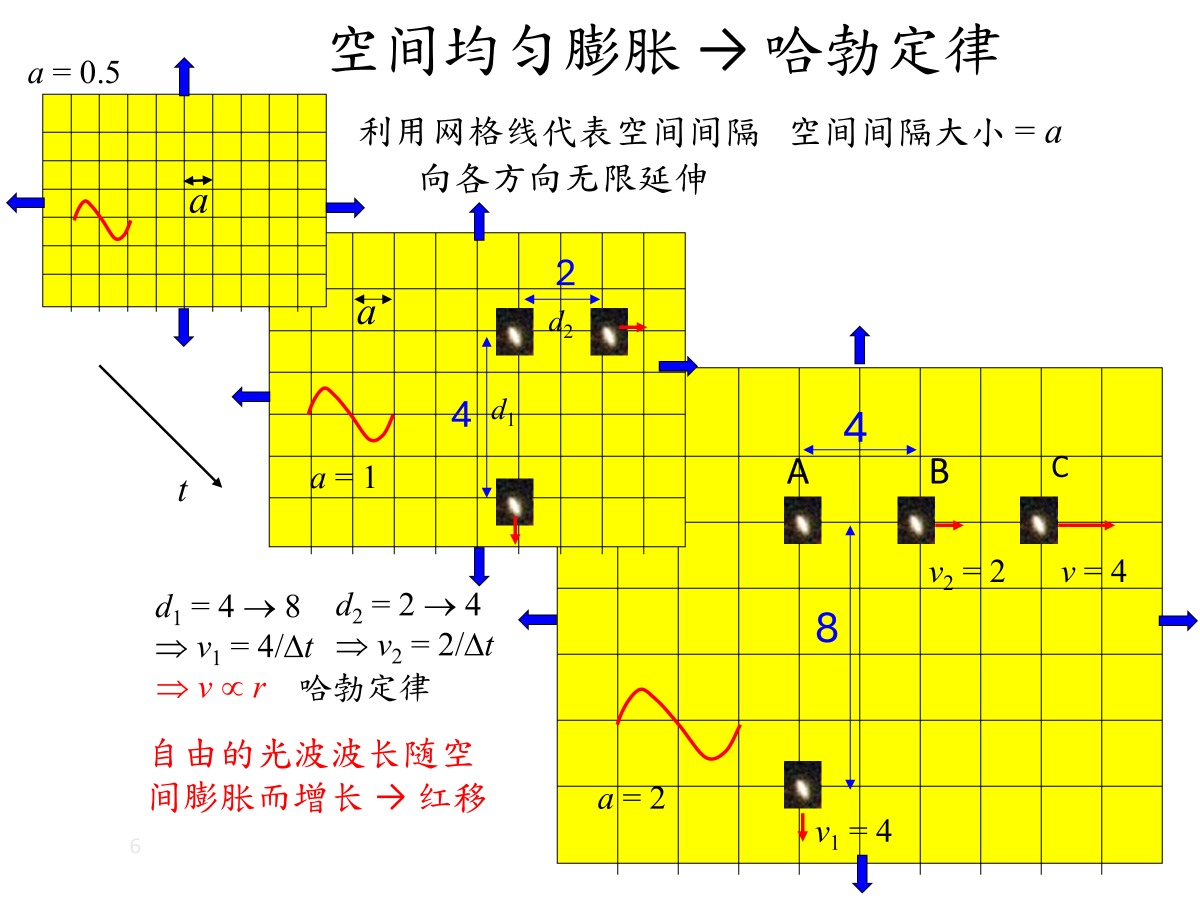
图 2 宇宙的膨胀应该理解为遥远星系之间的空间均匀膨胀。 我们可以一个网格来说明这个空间的相对大小，网格宽 度为a，并且随着时间的推移而增加。哈勃定律描述了 这种空间的均匀膨胀。这种理解与宇宙学原理和广义相 对论都是一致的。


让我们考虑星系B和C，它们在时间t = t₀ 时分别位于距离星系A相距2和4个单位的位置。当时间t = t₀ +∆t时，由于空间的均匀膨胀，从A到星系B和C的距离都增加了一倍，成为4和8个单位。 因此，从A的角度来看，星系B 和C似乎分别以 2/∆t 和4/∆t个单位的速度后退，这与它们的距离呈完美的比例关系。我们得出结论， v = Hd，其中H 是称为哈勃参数的比例常数。这关系被称为哈勃定律。在这个模型中，宇宙中的每个点都被认为是 一个膨胀中心，网格向各个方向无限延伸，确保宇宙保持均匀和各向同性。

由于宇宙的膨胀，物质和能量的密度会随着时间而降低。结果，宇宙从最初的热和致密状态演变成我们今天观察到的寒冷和弥散状态。哈勃参数 H也随时间而变化。宇宙学模型，例如暗能量冷暗物质 (ɅCDM)模型[3]，可以预测H 如何变化并描述宇宙的膨胀历史（见图3），这可以通过观测来检验。天文学家已使用各种方法测量现今宇宙的膨胀率，称为哈勃常数 H₀[4]。


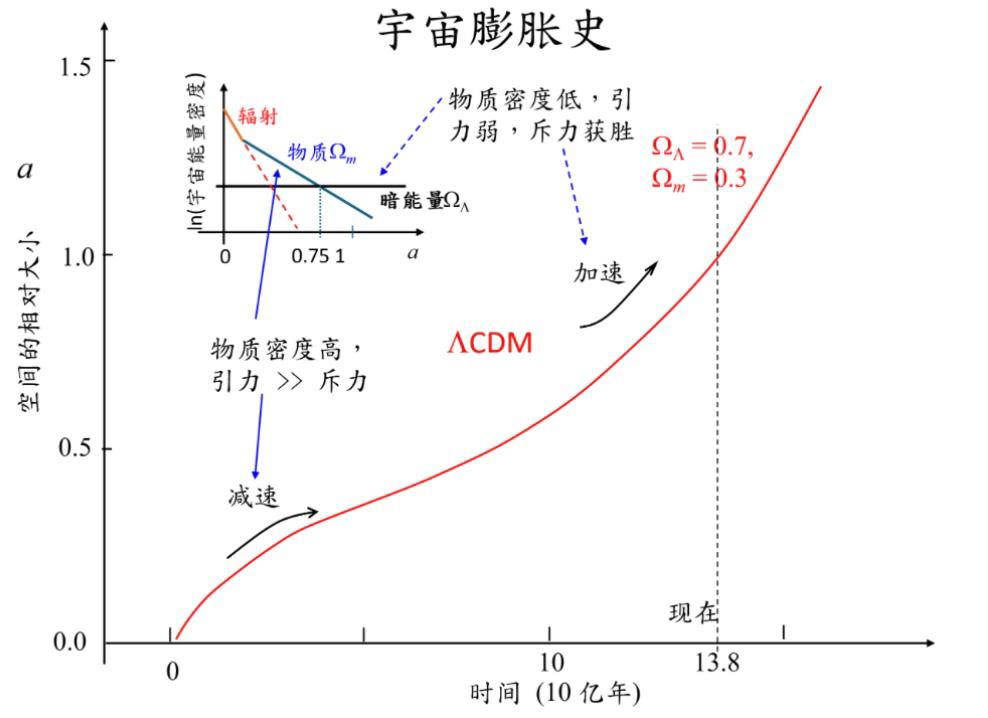
图 3 根据CDM绘制的宇宙膨胀历史草图。随着物质密度的下降，由于相互引力减弱，减速的早期膨胀过渡到晚期加速。


哈勃常数危机–标准宇宙学模型的挑战

最近，不同的哈勃常数的测量值出现了显著的差异[5]。 这些测量可以分为两类：基于来自相对较近的天体（如超 新星）的光的局域测量，以及基于对宇宙微波背景的观 测及采用标准宇宙学模型得出的全局测量。局域测量报告 的值约为73 ± 1 km/s/Mpc，这意味着两个相距1 Mpc （约330万光年）的星系以每秒73公里的速度彼此后退， 但全局测量更倾向于 67 ± 0.5 km/s/Mpc。

局域测量使用哈勃定律直接决定哈勃常数， H₀ = v/d。虽然近邻星体的沿视线速度v 可以通过其红移来测量，但要确定其距离d则颇具挑战性。 幸运的是，一些宇宙天体的本征亮度是已知的或可以很容易地测量到。 这些被称为标准烛光。例如，造父变星的亮度变化周期和本征亮度之间存 在紧密的相关性，前者相对容易测量。一旦知道了物体的本征亮度，与它 的视亮度的比较就会告诉我们它的距离，因为后者随着距离的平方而下降 。天文学家使用近邻的标准烛光，例如造父变星，通过多种方法进行交叉 检查其距离，因此更可靠，来校准距离较远的标准烛光，例如1A型超新星[6]。

这种局域测量并不依赖于特定的宇宙学模型。然而， 距离测量可能会出现系统误差，特别是因为「标准烛 光」是否真的是「标准」可能值得商榷。

此外，测得的星体红移未必完全是由于哈勃膨胀导致，因此不完全对应于 H₀d。任何宇宙天体都可能被其相邻天体吸引，以致其运动偏离哈勃膨胀 （见图4）。这种现象称为本动运动。换句话说（参考图2），我们不应该 假设星系一直卡在网格上。由于它们受附近的天体影响，它们也会相 对于网格移动。除了哈勃膨胀之外，星系的本动运动vp 亦会影响其视线速度v = vp + H₀d。虽然 H₀d 始终为正数，但 vp 可以是正数或负数。


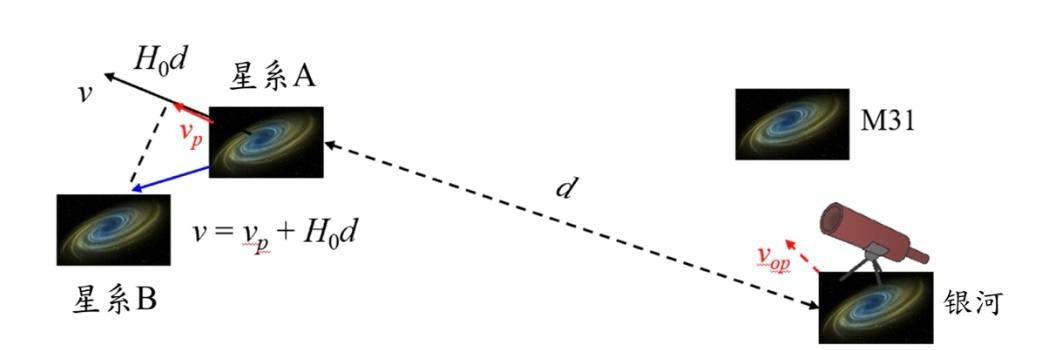
图4 我们观测到星系A与B的速度包含因它们相互作用引起的本动运动速度， vp。 银河系的本动运动，例如由于我们的相邻星系M31的吸引（红色虚线箭头表示），也会影响 H₀的局域测量。


根据宇宙学原理，不同宇宙天体的本动运动方向和幅度应为随机的 ，因此当对许多天体进行平均时，它们对H₀ 的贡献应该有效地相互抵消。然而，观测结果也受到观测者相对于 哈勃膨胀的本动运动的影响，观测者的本动运动不会通过多次测量 的平均值来抵消，从而导致H₀测量值的系统误差。

哈勃常数 (H₀) 的全局测量取决于从早期宇宙热等离子体 中的声波得出的标准长度。这种等离子体 在宇宙最早大约400,000年的时间对光子 不透明，在此期间，宇宙的温度高达约3000 K。 当宇宙膨胀并冷却到此温度以下时，等离子体转变 为中性氢气，类似于水蒸气在100 °C时凝结成液体 的状况。此时，从等离子体发射的光子就可以自由 地穿过中性气体，即所谓的光子退耦。

这些光子今天仍然存在，但它们的波长已经随着宇宙膨胀而 拉长了约1100 倍，形成了宇宙微波背景（CMB）[7]。WMAP 和Planck等任务已经精确测量了全天空CMB温度分布，提供 了光子退耦时宇宙微波背景天空的快照（见图5）。CMB中看似 随机的温度波动模式是由原始等离子体中激发的许多声波的相 互干涉产生的。这些波动的详细分析提供了有关宇宙的大量信 息，包括重要的宇宙学参数[8]。


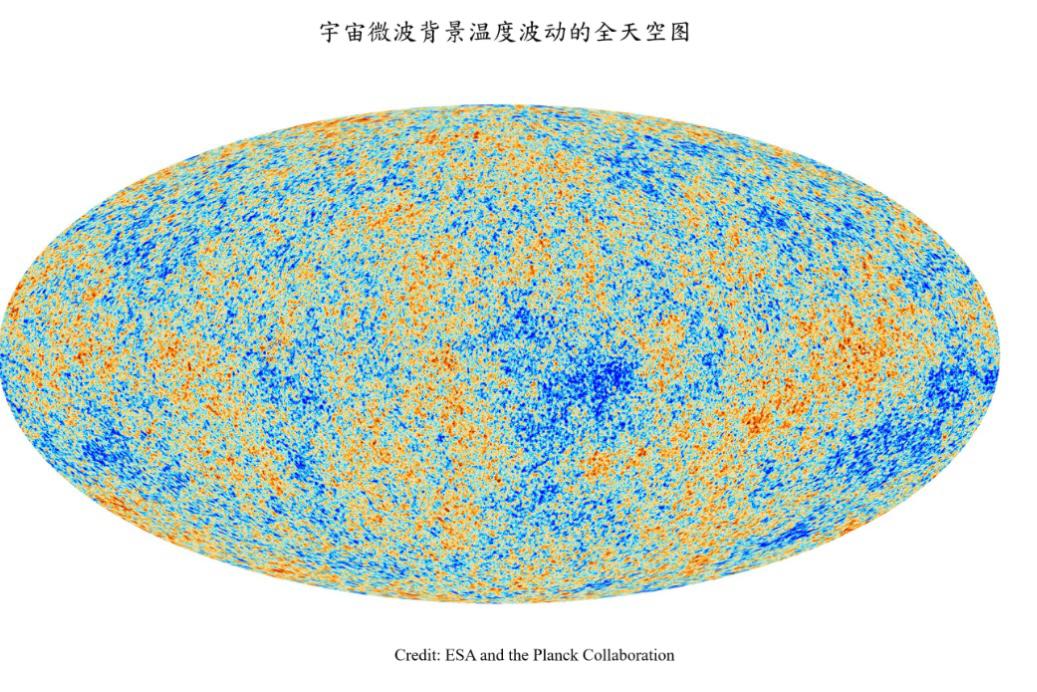
图5 宇宙约380,000岁时全天空CMB温度分布快照。 颜色表示略热（红色）到偏冷（蓝色），平均温度为2.725 K，涨落约为 10⁻⁴ K。 图片来源：ESA/Planck Collaboration。


这些声波的基本振荡模式，类似于由两端固定的琴弦产生的最简单的驻波，在CMB图上建立了大约1°的角度尺度 θ（见图6）。在这个尺度上，温度波动是显著相关的。而这个 θ 角的基线是光子退耦表面到我们的距离 D，这取决于自光子退耦以来宇宙的膨胀历史，因此受H₀影响，所以 H₀ 的数值与角度 θ 密切相关。虽然 θ 可以通过CMB观测进行高精度测量，但需要假设宇宙膨胀历史模型来估算 H₀。因此，H₀的全局测量依赖于 ɅCDM的正确性。


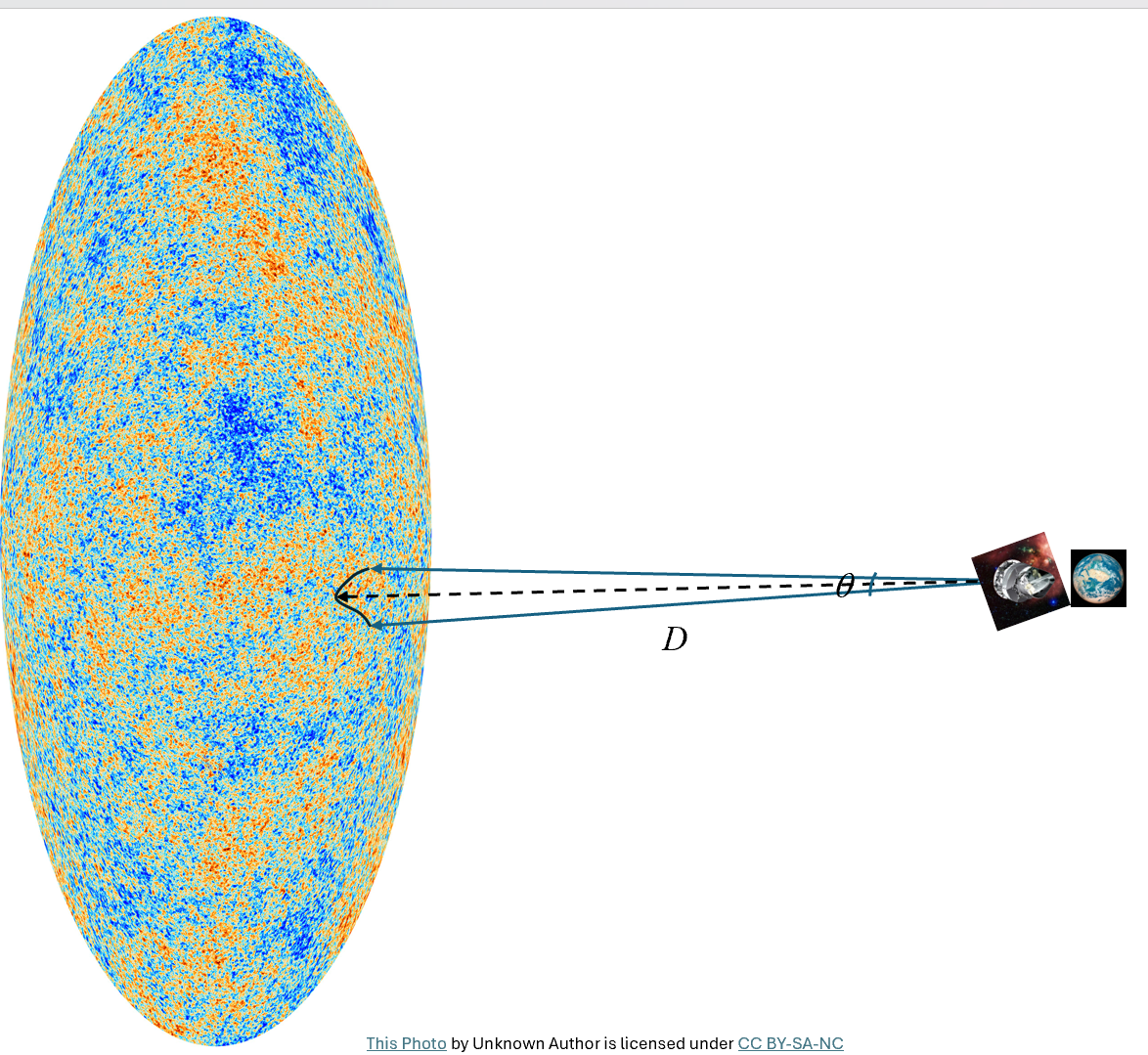
图6 测量CMB温度涨落与地球的相关角。光子退耦表面的声波振荡在距离D上形成一个角度θ。


哈勃常数危机引起了极大的兴奋和关注，因为它可能表明超越标准宇 宙学模型和粒子物理标准模型的新物理学的存在。例如，哈勃常数危 机的一个可能解决方案是引入以前未检测到的辐射（非光子和中微子） ，称为暗辐射。与 ɅCDM相比，这会改变宇宙的膨胀历史，并使CMB的哈勃常数测 量值与局域测量值保持一致。这种暗辐射的存在如果得到证实，将会 是基础物理的重要突破。

鉴于哈勃常数危机的重要性，研究人员亟需建立独立可靠的(H₀) 测量方法，以检查局域和全局测量值的异同。

揭开星系对的隐藏动态

香港中文大学物理系的团队最近进行的一项研究提出测 量哈勃常数的新方法[9]。该团队包括博士生章王政、 杨硕博士，以及合作者廖世鸿博士（2015年中大博士，现 职于中国国家天文台）和中国科学院大学的胡慧杰博士。 研究结果发表在《天体物理学期刊快报》（The Astrophysical Journal Letters）上，详细介绍了一种利用星系对相互运动以测量 H₀的新方法。

我们并非通过观察单个星系的视运动来测量 H₀， 而是关注星系对的相对运动。这些运动受到 它们相互引力作用和宇宙膨胀的影响。我们 使用了称为星系对速度的统计测量方法，以 量化星系对之间的相对运动，为宇宙的结构 和演化提供了重要观察工具。通过检查星系 对速度，我们可以推断出有关宇宙大尺度动 力学的关键细节，包括哈勃常数。

我们使用了先进的计算器模拟，称为宇宙学N体模拟， 来比较不同宇宙膨胀场景中的星系对速度。我们将这些模 拟的结果与从星系巡天收集的观测数据进行了比较，结果 表明，星系对速度可以用作 H₀的独立和准确测量，为哈勃常数危机提供了新的视角。

新的、更可靠的哈勃常数测量方法

新方法侧重于星系对内 星系之间的相对速度，有效地消减了常见的偏差， 包括观察者相对于宇宙膨胀的本动运动所引入的误 差。如图7所示，观测到的星系A和B的速度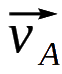， 和 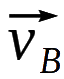，都包含观察者本动运动的相同贡献 (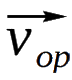)，但它们在星系A和B之间的相对速度中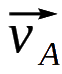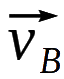， - ，恰好被抵消了。其他共存于 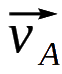和 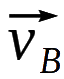的系统误差，例如观察者的仪器偏差，也在星系对速度中大幅抵消。 因此，该方法不仅可靠性更高，更能与现有的哈勃常数测量方法互补。


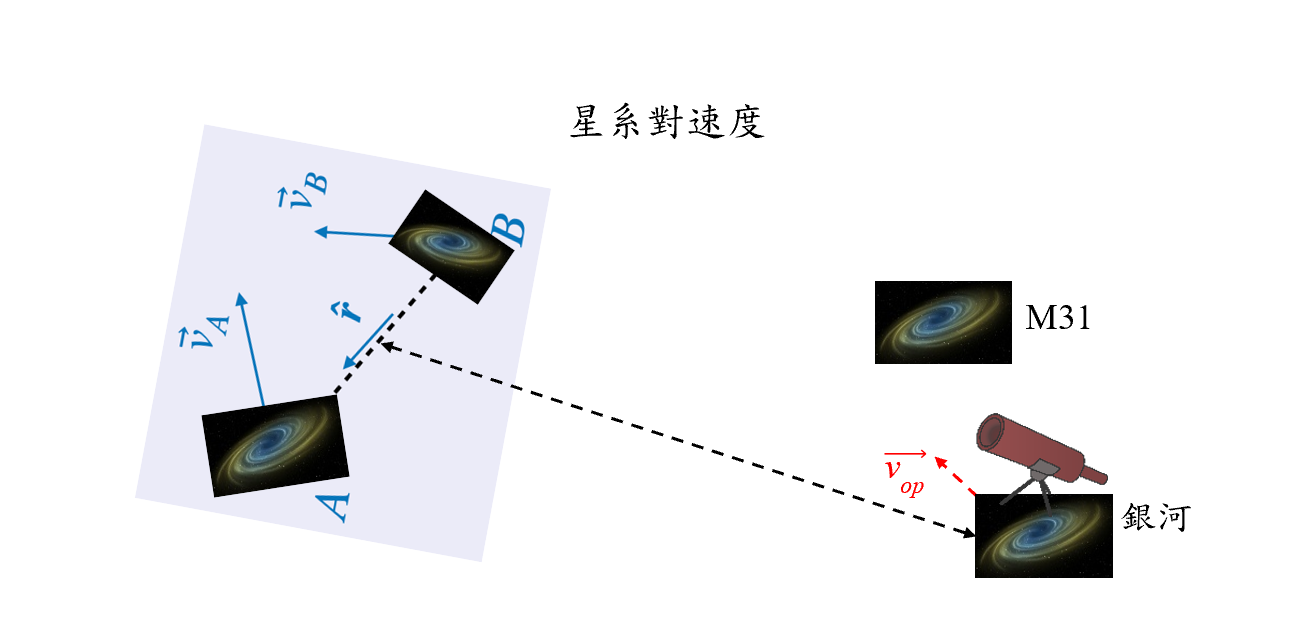
图7 星系对速度定义为两个星系（例如星系A和B） 沿其分脱机投影的相对速度，如虚线所示。由于观测到的星系A和B速度 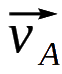（ 和 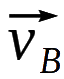），分别包含来自观察者本动运动的相同贡献，因此它们在相对速度中 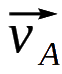- 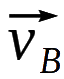抵消了。


新的测量将哈勃常数定为75.5 km/s/Mpc，误差为1.4 km/s/Mpc，约为2%。 此结果与其他局域测量值一致。这再次证实了哈勃常数危机，进一步挑战标 准宇宙学模型。

此外，由于星系的运动受到它们相互引力作用的影响， 因此星系对速度对物质密度也很敏感。使用新方法，我 们获得了宇宙学参数 Ωₘ的独立测量值，该参数表示物质在宇宙总能量密度中的占比。测量结果为 ❲Ωₘ❳ = 0.311，误差小于0.03，即9%。这一结果与CMB和其他宇宙学数据的测量值非常吻合[8]。

即将进行的大规模巡天，例如LSST[10]，将以更高的精度测量 更多的宇宙天体。因此，虽然我们的方法目前受到统计误差的 限制，但这些误差在未来会显著减少。使用我们的方法， H₀ 和 Ωₘ 的误差可以分别降低到0.6%和2%。

星系对速度是宇宙学中一个很有用的工具。它不仅帮助我们测 量哈勃常数和物质密度，还能够研究宇宙学中微子和其他假设 的轻暗物质粒子的影响。这些轻宇宙粒子的运动速度比冷暗物 质快得多，使它们把冷暗物质形成的大尺度结构平滑化。这反 过来又会影响物质之间的引力相互作用，我们可以通过星系对速 度测量来观察这些变化。

通过进行宇宙学N体模拟，我们都可以研究这些轻宇宙 粒子对星系对速度的影响。例如，我们利用这方法测量宇宙学 中微子的特性[11]，并限制了轻惰性中微子[12]的存在，这个 假设的粒子比熟悉的中微子[13]有更弱的相互作用。我们还在 努力采用星系对速度来量度中微子质量，中微子质量非常小， 即使是当今最好的实验室实验也无法直接测量它。

这就是宇宙学的美妙之处。宇宙进行了最大的实验供我们观察， 即使是最微小的粒子，如中微子，也会留下它们的痕迹。有了 更大、更先进的望远镜，我们可以观测到更多的宇宙历史，几 乎可以追溯到宇宙大爆炸。

理解宇宙的演化是人类伟大的追求，我们能够为此作出即使是 非常渺小的贡献，亦与有荣焉。

参考资料

    1. E. Hubble, “A relation between distance and radial velocity among extra-galactic nebulae”. Proceedings of the National Academy of Sciences, 15, 168 (1929).
    2. See for example, S. Weinberg, “Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity” (Wiley, 1972).
    3. See for example, https://lambda.gsfc.nasa.gov/education/graphic_history/univ_evol.html; https://ned.ipac.caltech.edu/level5/Peebles1/Peeb2.html
    4. For recent reviews, see R. B. Tully, “The Hubble Constant: A Historical Review,” https://arxiv.org/abs/2305.11950 ; W. L. Freedman, B. F. Madore, “Progress in Direct Measurements of the Hubble Constant,” https://arxiv.org/abs/2309.05618.
    5. For a recent review, see E. D. Valentino et al., “The CosmoVerse White Paper: Addressing observational tensions in cosmology with systematics and fundamental physics,” https://doi.org/10.48550/arXiv.2504.01669
    6. A. G. Riess et al., Astrophysical Journal Letters, 934, L7 (2022) and references therein.
    7. An excellent review of CMB physics can be found in https://background.uchicago.edu/~whu/araa/node1.html.
    8. Planck Collaboration, “Planck 2018 results. I. Overview and the cosmological legacy of Planck,” Astronomy & Astrophysics, 641, A1 (2020).
    9. W. Zhang et al., “Measuring the Hubble Constant through the Galaxy Pairwise Peculiar Velocity,” Astrophysical Journal Letters, 978, L6 (2025).
    10. Legacy Survey of Space and Time https://rubinobservatory.org/for-scientists/rubin-101
    11. W. Zhang et al., “Measuring neutrino mass and asymmetry with matter pairwise velocities,” Monthly Notices of the Royal Astronomical Society, 529, 360 (2024).
    12. R. Hu et al., “Impact of light sterile neutrinos on cosmological large scale structure,” https://arxiv.org/abs/2501.16908.
    13. B. Dasgupta and J. Kopp, “Sterile Neutrinos”, Physics Reports, 928, 1 (2021).

    作者：
    香港中文大学物理系朱明中教授

    2025年6月