過去數十年,隨著空中交通愈趨繁忙,降低飛機噪音是持份者需要面對的其中一項重大挑戰。但是要在飛行途中降低噪音,便可能會消耗更多飛機燃料,對於航空公司成本管理而言,這是一個必須考慮的因素。我們將會在本文提出一種規劃飛行航道的方法,當中的目標是降低人們感知到的噪音以及燃料消耗。我們將飛機的航跡分拆成地平面和高度兩條航道,以模擬航空運輸所面對的相關限制,並且會利用Dubins航道法及經改良的A*演算法,來找出地平面投影的最短航道,當中的演算法會根據飛行目的地、跑道角度、機場附近的飛機間隔、人口分佈,以及飛機轉向運動來考慮引導點。另外,我們亦會利用地平面航道計算出的距離,解構飛行運動的縱向公式來確定如何優化高度航道,從而降低人們感知到的噪音以及飛機燃料消耗。為了進行離散優化,我們設計了一個經改良的非支配型排序遺傳演算法II (NSGA-II),從而在減少運算難度之下得到最佳高度航道的帕累托前沿(Pareto fronts)。透過模擬從香港國際機場起飛,飛到兩個強制位置報告點來展示這個方法的成效。之後,我們會將結果與快速存取記錄器 (Quick Access Recorder) 的數據以及標準儀表離場(SID)程序的路徑進行比較。雖然這個方法並未考慮在航空運輸期間某些會令離場航道規劃受到影響的因素,例如天氣情況以及空中交通組合,但是得出的地平面航道卻與SID的路徑十分相似。由此得出高度航道的帕累托前沿,顯示可降低燃料消耗以及人們感知到的噪音水平。另外,我們亦根據不同航線的相關飛行物理學,分析了如何在燃料消耗和人們感知到的噪音水平之間權衡利弊。
I. 簡介
空中交通的迅速發展,及由此產生的飛機噪音的增加,導致居住在機場附近的居民飽受困擾,影響他們的睡眠,及出現與壓力有關的健康問題 [1]。這個問題可以透過飛機設計或空中交通管理等方法來解決 [2]。在飛機設計方面,我們可以設計新的飛機機體及引擎,以降低飛機發出的噪音 [3]。但自1980年代以來,要在不影響營運成本之下透過改變飛機設計來進一步降低噪音,是一件相當困難的事 [4]。至於空中交通管理方面,我們可以改變飛行航道以減少感知到的噪音,例如增加飛機起飛後的爬升率。雖然這個做法較為「務實」,但未能解決將飛機噪音降低的問題,同時可能會令燃料消耗增加 [5]。人們感知到的噪音以及燃料消耗,會受到引擎動力的設定以及飛機與觀察者之間距離的變化所影響,情況相當複雜 [6]。燃料消耗會直接影響航空公司的收入,同時亦與空氣污染及溫室氣體排放量成正比 [7]。因此,在優化航機的操作條件時,我們亦必須同時考慮人們感知到的噪音。
在實際情況下,機場四周的離場航道是以標準儀表離場(SID)程序作為指引。SID是指從離場航線開始的起點,直到航途階段中首個定位點/設施/航點的經編碼航行程序,不同的機場會有不同的SID [8]。各國民航當局均按照ICAO Doc. 8168 [8] 中訂明的設計標準來設計及公佈SID,當中考慮的因素包括但不限於跑道角度、地形、需避開的障礙物、飛機性能、空域管理以及環境問題。根據香港民航處(CAD),在設計SID時,有關人員會先與持份者(包括營運商/機師及空中交通管制員)進行初步討論。之後,便會在模擬飛行中測試初步路徑在不同天氣和承載量下的可飛程度,再在發佈該路徑前透過實際的航行測試來加以驗證。Zachary等人[9]、Prats等人[10]、Torres等人[11]、Ho-Huu等人[12]、Filippone等人[13],以及Thomas和Hansman [14] 進行了優化計算的研究,以在定量標準下改良離場航道的設計程序。這些研究建議採用多目標或多層次的起飛航道規劃方法,當中同時考慮到燃料消耗和感知到的噪音水平。然而,據我們所知,這些研究並未根據航行目的地(即本研究考慮的強制性[ATS]位置報告點)、由航行資料彙編(AIP)提供的障礙物限制,以及人口和地形的資訊,來考慮引導點所產生的綜合影響。其中有部分研究亦未有將其取得的結果,與現有的SID路徑或航班數據進行比較。為了彌補這方面的不足,本文在同時考慮上述所有因素下,提出了一個旨在帶來低噪音和低燃料消耗的起飛航道規劃方法。
優化具有多個變數限制的航道在電腦運算上是相當慢 [15]。在維持一定的計算效率,並同時在考慮多個不同限制下得出一組最理想的帕累托(Pareto)解決方案上,本研究帶來了三個貢獻。第一個貢獻是將四維航跡規劃(三維空間再加上時間)分拆成兩個子問題:1) 在主要考慮與地理/地形相關的限制(例如禁飛區、人口密集的非航行及升降區,以及航道角度限制)下,規劃投射在地球表面的最短航道;及 2) 在考慮與垂直飛行性能相關的限制下,沿著最短航道來規劃在不同速度下的高度航道,以降低累積的感知到的噪音水平和燃料消耗。採用分拆方法來規劃航跡,是最先是由 Kant 和 Zucker [16] 提出,以因應在包含靜態及移動障礙物的動態環境中所進行航跡規劃,簡化當中所面對的問題。他們的研究提出了一個序列規劃的方案,當中第一個步驟是解決航道的純空間優化問題,第二步則因應第一步所產生的航道,解決時間依存的速度問題。在此強調,首個空間解決方案不會被隨後的時間解決方案所影響。然而,由 Hartjes 和 Visser [17] 所提出的航跡分拆方法,均考慮了在兩個子問題中(即橫向及垂直航道規劃)的速度耦合。從垂直航道規劃中得出的飛機空速,限制了橫向航道規劃中的轉彎半徑。在他們的研究中,各航道是在訂明了從出發地到目的地之間固定數量的航段後確定出來的。橫向航道規劃中的航段類型,僅限於直線及恆定半徑的轉彎航段;而垂直航道規劃則受到航空站位置的固定高度及空速所限制。本文提出的航跡分拆方法,並不會對航道航段的類型或數量產生限制;而航空站的高度則是其中一個受 AIP 限度所限制的設計變量。藉着這些構思,我們便能廣泛地研究設計空間,並且透過分拆方法來簡化多目標的優化工作。我們將本研究中的四維航跡規劃,分拆成地平面航道及高度航道,並以地平面航道的弧長連結起來。當在地平面航道規劃中解決了將這個弧長減到最短的最短航道問題後,便會估算高度航道規劃中燃料消耗及累積的感知到的噪音水平。在地平面航道規劃中,我們單獨地考慮了在不運用速度耦合下可能會被忽略的轉彎半徑限制。
本研究的第二個貢獻,就是為最短航道規劃提出一個嶄新的方法,讓我們能考慮非可取區域、禁飛區以及航道角度的限制。在文獻中,大部分模擬航道規劃都已經能夠避開靜態障礙物(這些障礙物是一些航跡無法越過的地形和地理限制)的航道 [18-21]。除了靜態障礙物外,我們的方法亦引入了非可取程度。非可取程度的估算涉及整個航道規劃範圍,得出的解決方案往往會將航道改變至非可取程度較低的區域。由於本研究中的非可取程度是根據人口分佈來確定,因此我們認為在人群可能受到飛機噪音影響較大的區域附近,非可取程度會較高。我們將這種非可取情況稱為勢場的排斥力,是其中一種航道規劃方法。航道規劃方法大致分成四種類型 [22]:1) 以網格為基礎的網絡 [18、23]、2) 以採樣為基礎的方法 [19、20]、3) 勢場 [21、24],及 4) 最佳控制理論 [25、26]。以網格為基礎的網絡能在起點和目標之間訂明的網格上解決最短航道的問題。雖然透過這個方法將資訊匯聚起來並不複雜,但是視乎網格的形狀,這個方法可能不符合物理要求 [27]。至於以採樣為基礎的方法則是以樣本空間,而非透過在預先建立的網格上進行搜尋來找出最佳航道 [28]。雖然這個方法可在短時間內計算出結果,但卻可能會在進行大範圍規劃時產生出效率欠佳的航道 [29]。勢場方法能模擬朝著目標移動的物體,當中會將目標模擬成具有吸引力的區域,而障礙物則為具有排斥力的區域 [30]。由於計算時間短,因此這些方法適用於實時航道規劃,但答案可能會趨向於局部最小值 [31]。最佳控制方法是根據運動控制公式來優化特定性能指標。其中所產生的航道雖然符合物理要求,但是收斂卻未必保證成功 [32]。最近的各種做法已經將這些方法組合起來,以彌補它們各自的缺點 [33]。舉例來說,將以網格圖形和採樣為基礎的方法結合,以平整前者因網格規範而產生出不符合物理要求的航線。我們在本研究中結合了這四種方法,以能在快速且符合物理要求的情況下規劃地平面航道,從而模擬出各種航空運輸限制。首先是將Dubins航道(最佳控制方法)應用到靠近跑道的 SID 程序開始部分。由於跑道角度和飛行航線的飛機間隔要求嚴格限制了起飛航道,因此引入Dubins航道,以模擬具有開始航向和航空站航向限制的起飛航道規劃。第二步是提出一個以人口密度為主要考慮下,在Dubins航道終點到目標之間包含轉向限制的考量人口因素A*演算法。這個演算法將勢場和以採樣為基礎的方法,納入到以網格為基礎的方法中。A*演算法是一種以網格尋找最短航道的常用方法,由於它完整、易於修改以及能夠快速計算,因此我們的方法亦按此制定出來。正如上文所述,由於我們會將以人口密度為基礎的勢場方法結合至 A* 演算法中,因此便能在量化的感知到的噪音水平下因應人口來規劃最短航道。根據以採樣為基礎的方法,我們的方法透過搜尋樣本空間來平整航道。我們在這個樣本空間搜尋中引入了航道角限制,以協助處理與飛機適航性相關的因素。透過將這些方法結合,便能令我們的做法更為實際,並且能配合現實世界的應用情況。
最後一個貢獻,就是在整數規劃下透過多目標優化來找出高度航道。在規劃地平面航道後,我們便會沿著將累積的感知到的噪音和燃料消耗降到最低的地平面航道,來計算高度航道。由於燃料消耗和累積的感知到的噪音水平耦合在一起,因此在沒有預先訂明取向的情況下,將兩者降到最小的解決方案並不能產生出最佳航道 [6]。這些解決方案會以帕累托前沿集 Pareto front set 的方式表達,當中顯示了決策過程中權衡利弊的敏感程度。假如設計變量的數目較少以及無法準確知道目標函數剖面,則帕累托前沿集主要會透過進化演算法得出,繼而無法保證連續性。透過進化演算法來優化多個目標需要很長的計算時間 [17],並且難以收斂。為了解決這個問題,我們將設計變量限制為具有預先訂明均勻區間的整數,其中區間是合理地根據每個變量的物理意義而選取的。這個範圍的限制避免了為相對不顯著的變化進行函數估算,例如,一米內的高度變化。此外,在這種設定下,由於設計空間的大小可以透過有限數量的設計變量來估計,因此我們可以合理地設定進化演算法中的函數估算次數。
總括而言,我們制定了一個能優化多目標飛行航道的方法,當中考慮了各種實質限制,以模擬離場期間航空運輸的操作。另外亦將四維的飛行航道規劃分拆成依次的地平面和高度航道規劃程序,從而減少計算時間。我們提出了根據飛行目的地、靜態障礙物、跑道角度、機場附近的飛機間隔、以人口分佈為基礎的非可取區域,以及轉向限制來考慮引導點的地平面航道規劃;同時亦制定了具有整數規劃的高度航道規劃,以能有效率地進行運算。我們承認目前所制定的方法仍然存在局限性,如在模擬航空運輸中影響離場航道規劃的天氣和空中交通組合。透過我們的方法,我們規劃了從香港國際機場飛往兩個不同目的地的飛機航道結果顯示找出來的路徑與 SID 路徑非常相似。因此,本文提出的方法仍然能為決策過程提供幫助,以在考慮航空運輸所面對的限制下,確定降低燃料消耗和感知到的噪音的離場飛行航道。
本文的結構如下。第 II 節詳細說明與飛行航道規劃、多目標優化,以及燃料消耗和噪音預測模型有關的方法。第 III 節因應在兩個出發地與目的地之間採用我們所制訂的方法,闡述當中的結果和討論,並將結果與實際的航跡數據進行比較和驗證。第 IV 節總結本研究的發現結果並提供結論。
II. 研究方法
本節介紹一個能降低感知到的噪音水平和燃料消耗的飛行航道規劃方法。飛行航道是指飛機的航跡,根據世界大地測量系統1984 [34],其以地平面坐標和高度表示。在本研究中,我們將飛行航道分拆成地平面航道和高度航道,其中地平面航道是指飛機在地球表面上的平面投影位置;而高度航道則指飛機在以弧長(在地球表面的累積飛行距離)和高度作為坐標之下於表面上的投影位置。地平面航道和高度航道與累積飛行距離(在地平面航道規劃中率先減至最短)結合。當在根據航行規則、轉向角度、該地區中居民人數的既定限制下產生出最短地平面航道後,便根據在固定距離位置(與表面弧長對應)的高度變化,得出降低感知到的噪音和燃料消耗水平的最佳高度航道。第 II. A 節詳細說明地平面航道的規劃方法,而第 II. B 節則詳細解釋高度航道的規劃方法。
A. 地平面航道規劃
飛機在進入或離開任何國家空域時,必須在由航空情報服務 (AIS) 指定的位置聯絡航空交通管制(ATC)塔;此位置稱為強制位置報告點。本節詳細說明從起飛到 ATS 位置報告點的地平面航道規劃方法。所制定的地平面航道規劃方法會依次以兩個階段執行航道規劃:初步離場階段及後續離場階段。初步離場階段在跑道至定位點開始,其中定位點位於在 AIP 中所描述的直飛定位段上 [35]。在機場附近的首個直飛定位段,其指定端點視為飛機的橫向飛機間隔,以供 ATC 在類近時間於各跑道離場期間管理空中交通。後續離場階段是指從這個定位點至強制位置報告點的航行階段。
第 II.A.1 節介紹用作計算地平面航道模型的方法。第 II.A.2 節詳細說明解決 AIP 所定義的高海拔區域,以及禁飛區,限飛區及危險區的方法‡。第 II.A.3節介紹初步離場階段的地平面航道規劃。第 II.A.4 及 II.A.5 節詳細解釋後續離場階段的地平面航道規劃方法,其中考慮了包含轉向限制的人口分佈及航道平整問題。
1. 網格的產生
我們將飛機航跡在地球表面上的投影映射到網格上,以模擬整個地平面航道規劃。這個網格是根據地理資料產生。首先,我們會將以測地坐標來代表的地理資訊,轉換成笛卡兒坐標。透過指定四個在地球表面的經緯度點,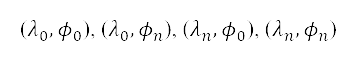 來定義航道規劃區域的邊界,使封閉的地區能涵蓋離場機場及目標的強制位置報告點。之後,我們將測地坐標轉換成笛卡兒坐標
來定義航道規劃區域的邊界,使封閉的地區能涵蓋離場機場及目標的強制位置報告點。之後,我們將測地坐標轉換成笛卡兒坐標
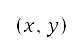 。 將
。 將 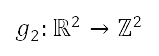 定為從測地坐標換成笛卡兒坐標的坐標變換,定義如下
定為從測地坐標換成笛卡兒坐標的坐標變換,定義如下
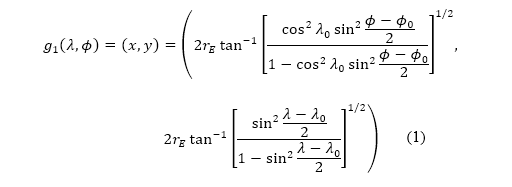
其中 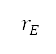 是地球的半徑,而
是地球的半徑,而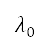 及
及 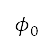 分別表示邊界左下角的緯度和經度。坐標變換
分別表示邊界左下角的緯度和經度。坐標變換 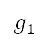 是從目前位置
是從目前位置 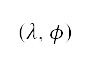 至
至 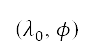 及
及 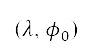 的半正弦距離 [36]
得出。第二步,我們將這個笛卡兒空間離散化,並將映射定義到網格上。笛卡兒領域的軸以均勻區間
的半正弦距離 [36]
得出。第二步,我們將這個笛卡兒空間離散化,並將映射定義到網格上。笛卡兒領域的軸以均勻區間 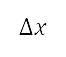 及
及
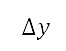 離散開來,以產生網格點。將
離散開來,以產生網格點。將 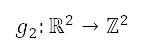 定為從笛卡兒坐標
定為從笛卡兒坐標 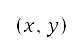 的坐標變換變成網格點
的坐標變換變成網格點 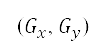 ,定義如下
,定義如下
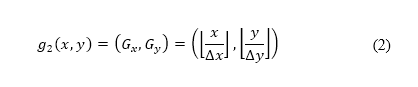
將 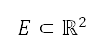 定為代表,地平面航道航跡優化問題的有限領域。將
定為代表,地平面航道航跡優化問題的有限領域。將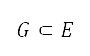 定為
定為 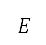 的限制並變成整數,其定義了網格的領域。將以測地坐標表示的空中運輸調節限制,透過函數
的限制並變成整數,其定義了網格的領域。將以測地坐標表示的空中運輸調節限制,透過函數 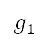 及
及 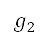 的複合映射到網格上﹐定義如下
的複合映射到網格上﹐定義如下
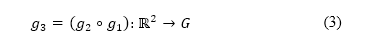
由於 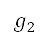 不可逆轉,因此隨後出現的符號
不可逆轉,因此隨後出現的符號 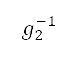 表示它的右逆向,這是包含映射的整數坐標作為
表示它的右逆向,這是包含映射的整數坐標作為 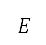 的子集。
的子集。
2. 障礙物的限制
我們在方法中產生的地平面航道,考慮了所有禁飛區情況。禁飛區是飛機不得飛行的區域,例如在 AIP 中指定的禁飛,限飛和危險區域,以及地面高度高於海拔 500 米的區域。圖 1
顯示了香港空域中的禁飛區及其在網格上的表示方式。我們的方法將禁飛區視為包含障礙物限制的區域。圖 1
左邊顯示了分為四種類型的障礙物:點障礙物,具半徑的點、區域邊界頂端上的點,以及地圖邊界。點障礙物是指地面高度高於海拔
500 米的區域,並以紅點表示,當中的數據是位置 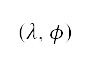 ,資料擷取自 Google Earth§
,包含點的取樣;並透過
,資料擷取自 Google Earth§
,包含點的取樣;並透過 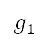 .
轉換成笛卡兒坐標。具半徑的點以及區域邊界頂端上的點在圖 1
以左邊的藍線表示,與 AIP 中所列出的禁飛,限飛及危險區域對應。這些點亦利用
.
轉換成笛卡兒坐標。具半徑的點以及區域邊界頂端上的點在圖 1
以左邊的藍線表示,與 AIP 中所列出的禁飛,限飛及危險區域對應。這些點亦利用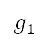 進行轉換,然後應用於幾何公式中,例如與圓形和線段對應的幾何公式,以確定圖中以藍線圍著的區域所包括的點。為了限制網格中的飛行航道,我們亦將地圖邊界模擬成障礙物,以將其視為受限制區域。將
進行轉換,然後應用於幾何公式中,例如與圓形和線段對應的幾何公式,以確定圖中以藍線圍著的區域所包括的點。為了限制網格中的飛行航道,我們亦將地圖邊界模擬成障礙物,以將其視為受限制區域。將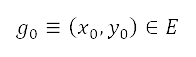 定為障礙物的位置。將
定為障礙物的位置。將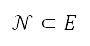 定為
定為 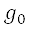 的鄰接區,以使
的鄰接區,以使 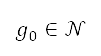 。這個鄰接區代表了圍繞著障礙物的區域,我們將其定義為障礙物區域。將
。這個鄰接區代表了圍繞著障礙物的區域,我們將其定義為障礙物區域。將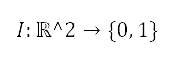 定為代表估算違反限制的指標函數。以下公式定義了障礙物區域的限制違反指標:
定為代表估算違反限制的指標函數。以下公式定義了障礙物區域的限制違反指標:
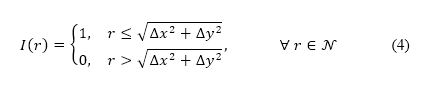
其中從點 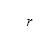 到障礙物
到障礙物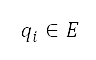 的距離
的距離 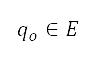 ,是以歐氏範數
,是以歐氏範數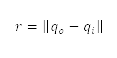 來確定。上述四種障礙物類型的限制違反,均由公式 (4) 來估算,而它們的位置則透過
g映射到網格中。這個過程所產生的障礙物區域,在圖 1 的右邊以深藍色表示,而白色區域則代表許可區域。透過防止飛機越過網格上這些限飛區域,來限制地平面航道。
來確定。上述四種障礙物類型的限制違反,均由公式 (4) 來估算,而它們的位置則透過
g映射到網格中。這個過程所產生的障礙物區域,在圖 1 的右邊以深藍色表示,而白色區域則代表許可區域。透過防止飛機越過網格上這些限飛區域,來限制地平面航道。
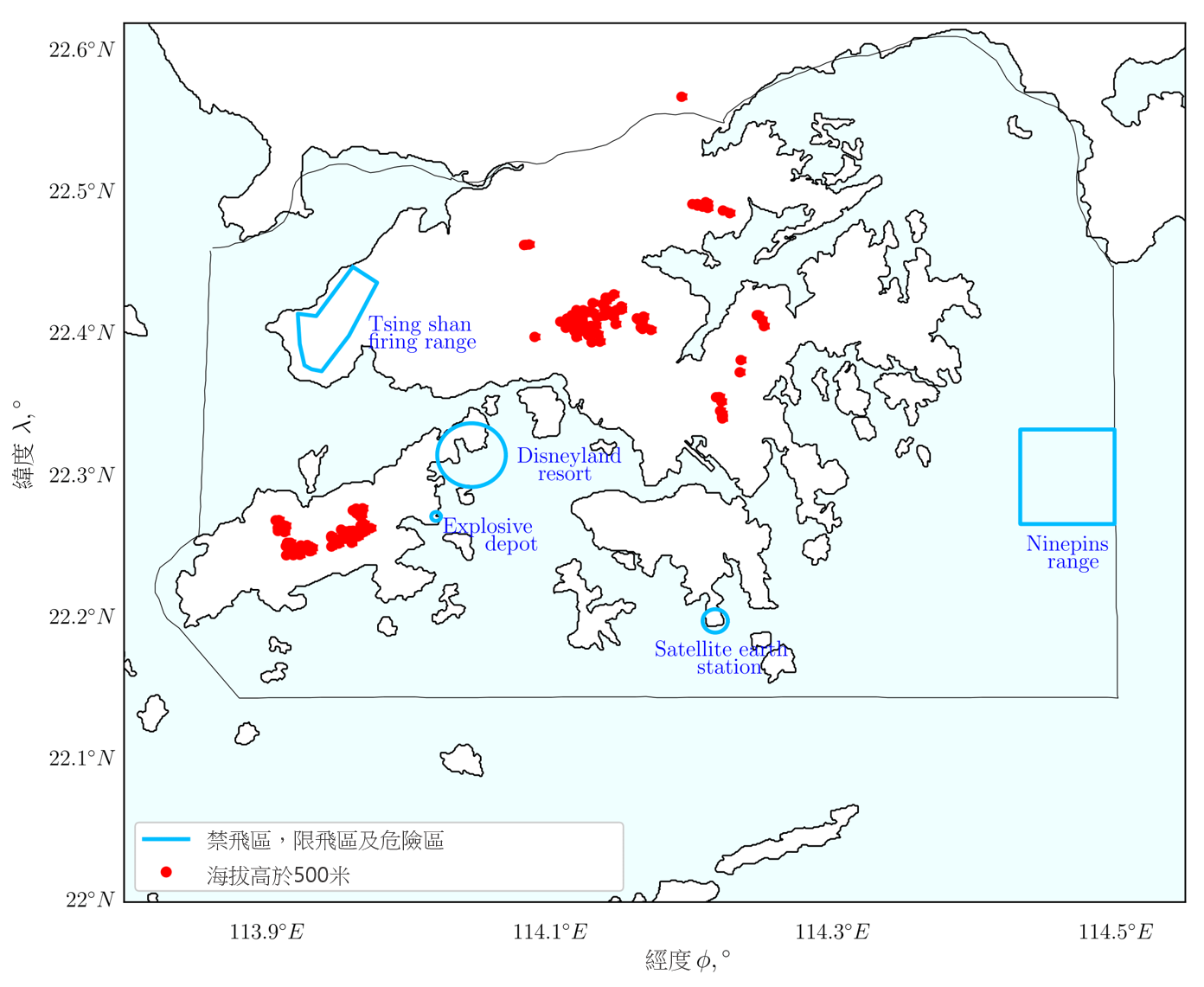
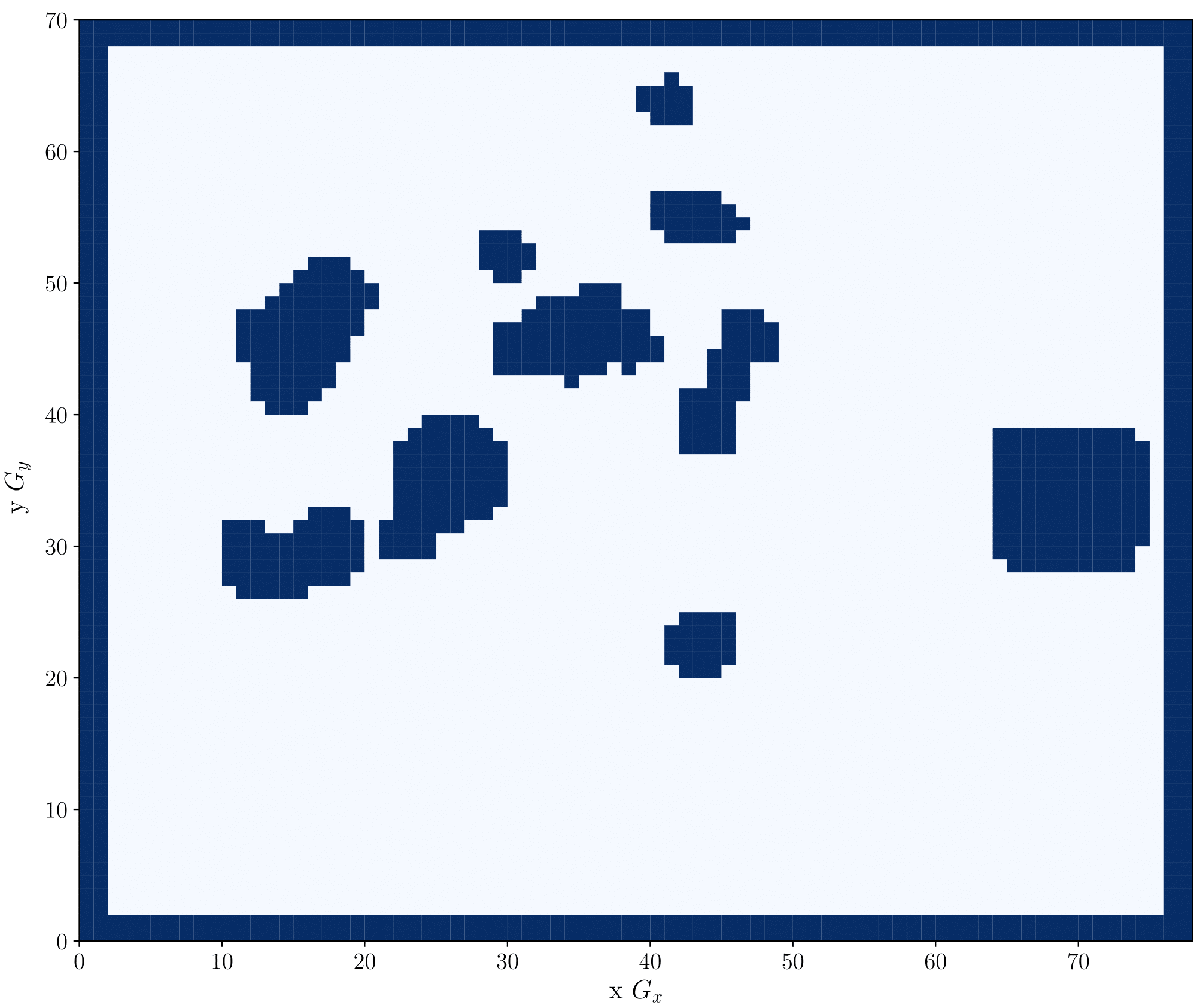
圖 1:以大地測量坐標系顯示的香港空域禁飛區(左)及使用公式 (4) 以在網格上產生相應的障礙物(右)。
3. 初步離場階段規劃
初步離場階段的航跡,受到跑道角度以及首個直飛定位段的方向所限制。舉例而言,香港國際機場設有兩條平行跑道,如圖 2 左邊所示。在圖中,「25L/R」表示左右跑道,其航向角度為 250°;「07L/R」表示左右跑道的航向角為 70°。因應機場附近的飛機間隔,香港民航處指定了六個初步離場航道,從兩條跑道的其中一條到三個定位點的其中一點,如圖 2 右邊所示。**香港 AIP 中的每個 SID 路徑,均包括這六條飛行航道的其中一條,因此,我們在本研究中將其視為初步離場航道的限制。
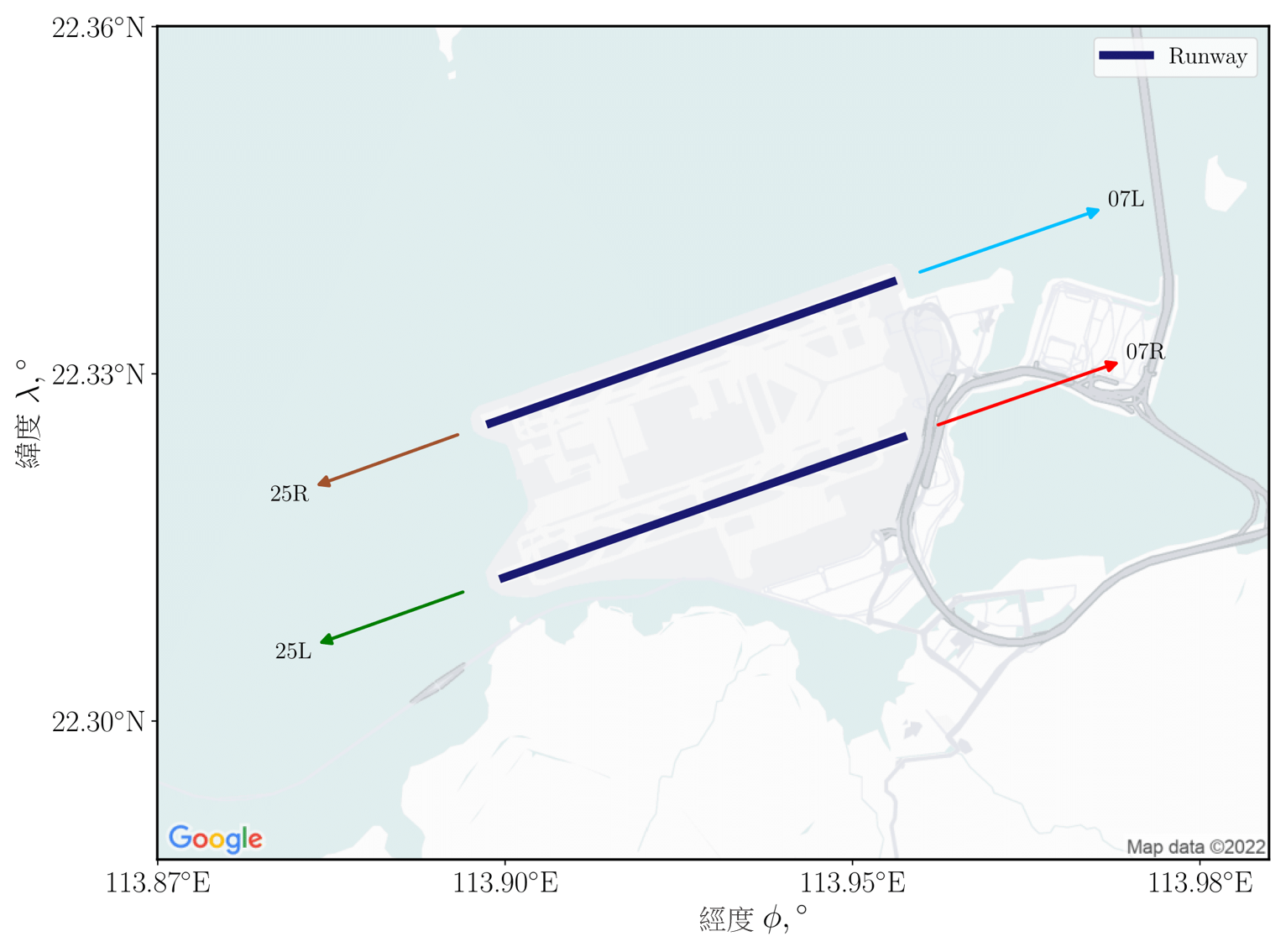
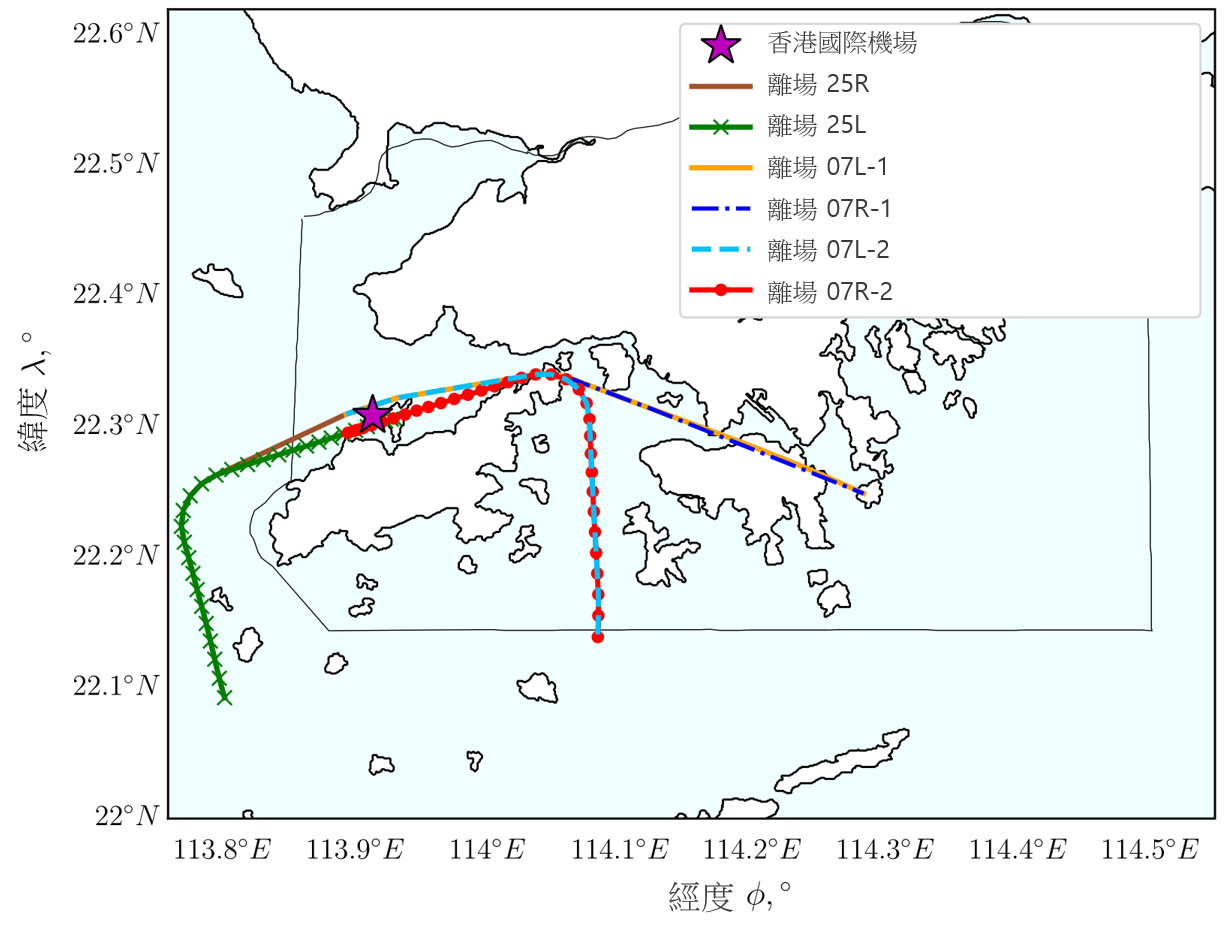
圖 2:香港國際機場的跑道配置(左)及從香港國際機場跑道至直飛定位段終點的六條初步離場航道(右)
我們採用Dubins航道方法,以模擬初步離場航道限制。這條航道是空間中連接兩點的最短曲線,其中航道的曲率是受到轉向/航向角度限制 [37] 。它可在起點和終點的方向上實施切線限制
[38]。這些特點讓我們擁有一個方便的框架,以產生與跑道平行並且朝著直飛定位段方向的航道。圖 3 顯示了Dubins航道的六個配置例子。這些航道是 R-L-S 曲線的複合,其中R 是右轉、L 是左轉、S
是直線。Dubins航道法首先產生六條航道,當中包含既定的起點 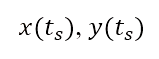 及終點
及終點 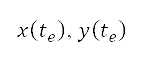 以及相應的航向角度
以及相應的航向角度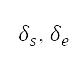 。 這個過程與公式 (5) 中所示的微分公式系統的解答對應,而航道距離 D 則以公式 (6)
透過以下解答來估算
。 這個過程與公式 (5) 中所示的微分公式系統的解答對應,而航道距離 D 則以公式 (6)
透過以下解答來估算
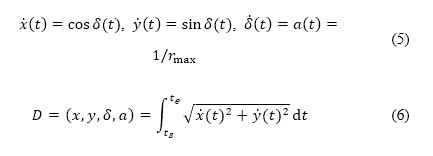
其中的點符號(例如 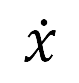 )表示時間導數,
)表示時間導數,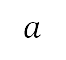 是被最大航向半徑限制的航向率
是被最大航向半徑限制的航向率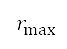 ,
,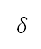 是航向角度,這是單位切線向量
是航向角度,這是單位切線向量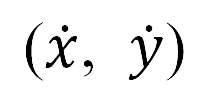 與
與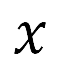 軸之間的角度。 我們選擇了具有最短距離的航道。
軸之間的角度。 我們選擇了具有最短距離的航道。
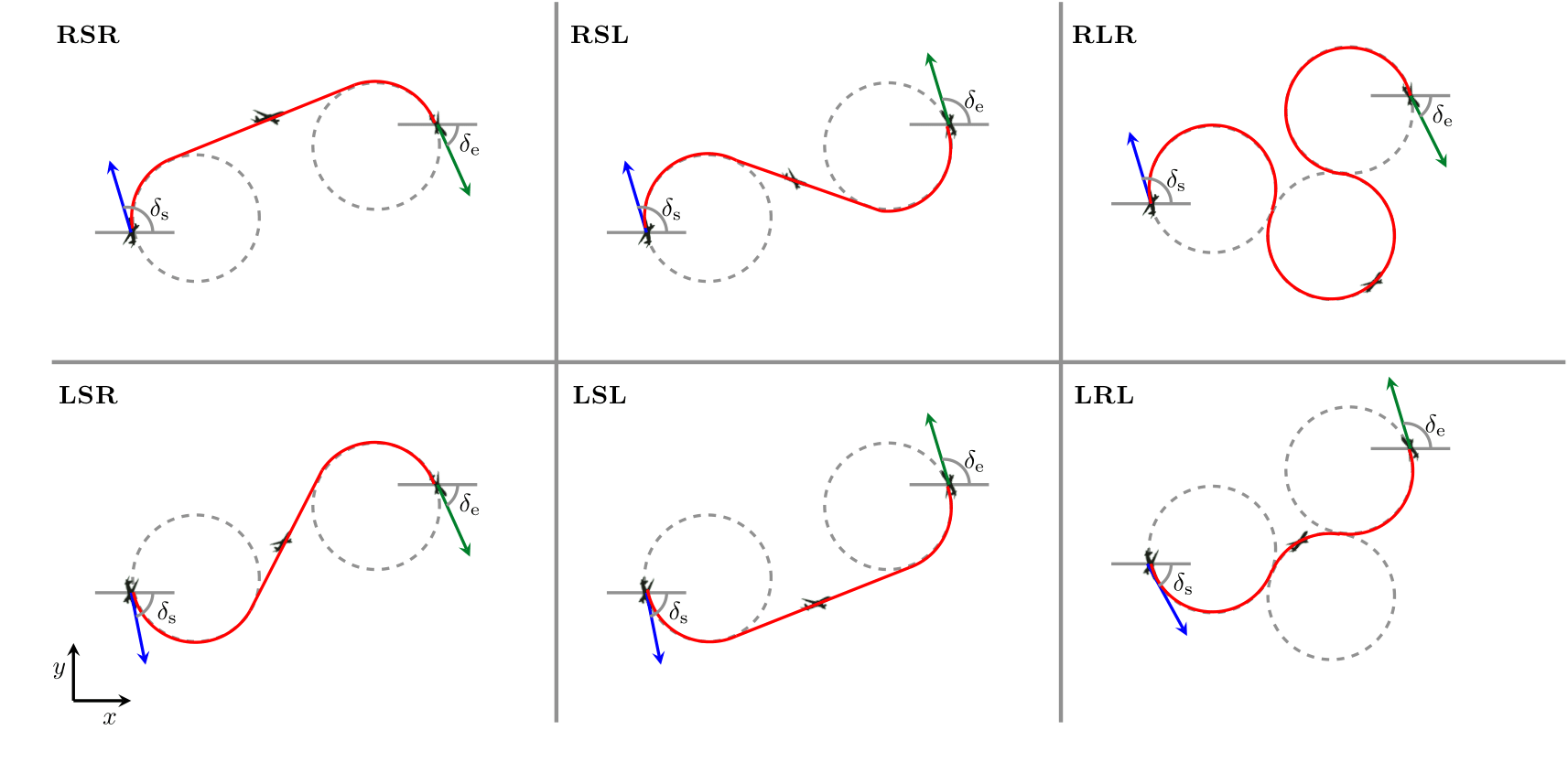
圖 3:包括起始和終結航向角度限制(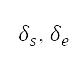 )的六個杜賓斯航道配置,其中 R、L、S
分別代表右轉、左轉和直線
)的六個杜賓斯航道配置,其中 R、L、S
分別代表右轉、左轉和直線
4. 包括考量人口因素限制的後續離場階段規劃
對於需要考慮噪音影響的飛行航道規劃,我們應優先考慮在人口密集地區降低感知到的噪音。有別於不允許飛行的禁飛區,在這些地區雖然飛機仍然可以飛越人口密集的地區,但並不是可取的選擇。為了在航道規劃中反映這個特徵,我們在
A*演算法中加入了勢場公式。A*演算法透過估計當物體從 起點移動至目標時在網格上所航行的距離,來找出於最低成本下在網格上的最短航道 [39]。A*演算法的代價函數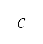 表達如下
表達如下
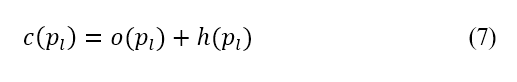
其中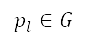 是網格上沿著航道的下一個節點、
是網格上沿著航道的下一個節點、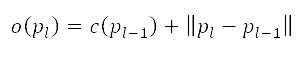 是從起始節點
是從起始節點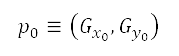 到
到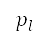 的航道成本,而
的航道成本,而 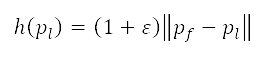 是一個探索成本,表示從
是一個探索成本,表示從 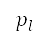 至目標
至目標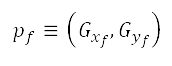 的最便宜成本航道,其中包括最終決定因素
的最便宜成本航道,其中包括最終決定因素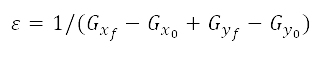 。與標準勢場方法不同,在我們的方法中人工勢場僅使用排斥力來構成,並沒有為目標模擬吸引力。我們稱之為考量人口因素
A*
方法。在公式 (7) 中,排斥勢是用作代價函數的加權因子。考慮排斥勢和最短航程距離的經修正代價函數
。與標準勢場方法不同,在我們的方法中人工勢場僅使用排斥力來構成,並沒有為目標模擬吸引力。我們稱之為考量人口因素
A*
方法。在公式 (7) 中,排斥勢是用作代價函數的加權因子。考慮排斥勢和最短航程距離的經修正代價函數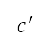 ,是從以下公式得出
,是從以下公式得出
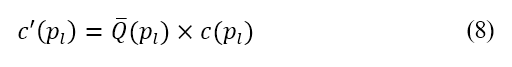
其中 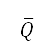 是標準化的排斥勢,是根據當地人口數據計算,如下所述。為了取得人口數據,我們採用了行政單位中心位置,以及來自
NASA 社會經濟數據及應用中心††的人口估計值。人口數據以中心位置
是標準化的排斥勢,是根據當地人口數據計算,如下所述。為了取得人口數據,我們採用了行政單位中心位置,以及來自
NASA 社會經濟數據及應用中心††的人口估計值。人口數據以中心位置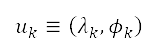 、面積
、面積 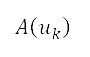 以及次級行政單位的人口估計值
以及次級行政單位的人口估計值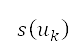 來表示。我們將排斥勢的來源放在每一個相應次級行政單位的中心位置,並以圓形表示。透過考慮
來表示。我們將排斥勢的來源放在每一個相應次級行政單位的中心位置,並以圓形表示。透過考慮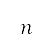 的多個來源,以在網格
的多個來源,以在網格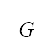 上每一個點的這些
上每一個點的這些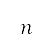 來源所產生的影響總和來找出勢場。在測量點
來源所產生的影響總和來找出勢場。在測量點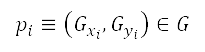 的排斥勢
的排斥勢 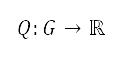 會受到位於
會受到位於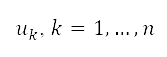 的來源所影響,其中強度
的來源所影響,其中強度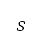 是以位於
是以位於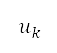 的人口估計值得出,如上所述。位於
的人口估計值得出,如上所述。位於 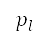 的勢(由位於
的勢(由位於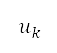 的單一來源觸發)亦會受到來源
的單一來源觸發)亦會受到來源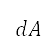 的距離影響,而半徑
的距離影響,而半徑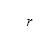 對應於有效區域A,透過下級行政單位的循環表示以
對應於有效區域A,透過下級行政單位的循環表示以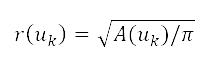 計算。前往來源
計算。前往來源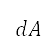 的距離是透過半正矢公式 (Haversine's formula) 計算 [36]。我們發現
的距離是透過半正矢公式 (Haversine's formula) 計算 [36]。我們發現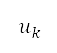 是測地坐標。網格上
是測地坐標。網格上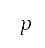 及
及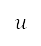 之間的轉換,是從
之間的轉換,是從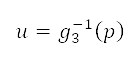 得出 [見公式 (3)] ,以能一致地測量距離。考慮所有這些項目的勢場
得出 [見公式 (3)] ,以能一致地測量距離。考慮所有這些項目的勢場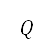 ,可表達如下
,可表達如下
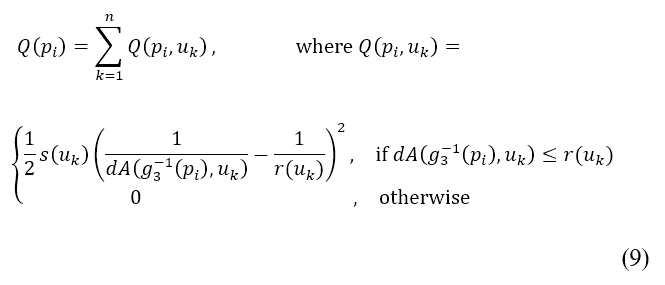
由於來源並不被視為障礙物,因此飛機的航道仍然可以越過其區域。換句話說,排斥勢的大小,不應導致在航道規劃中採用的代價函數在極限上接近零或無限大。透過將排斥勢標準化至範圍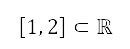 來加入這個限制,其中標準化的計算如下
來加入這個限制,其中標準化的計算如下
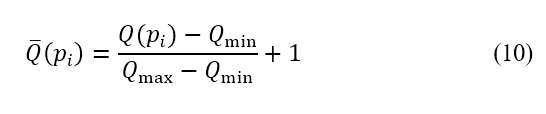
其中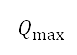 和
和 分別是整個勢場最大和最小的排斥勢值。根據上文提及與香港空域有關的例子,我們提出的勢場是利用香港的人口數據來計算。圖
4
左邊顯示了人口分佈;而右邊則顯示了按照人口而計算的勢場。右邊顯示的排斥勢,在概念上是在各個來源中人口密度影響的疊加,並且是根據左邊顯示的人口分佈計算出來。
分別是整個勢場最大和最小的排斥勢值。根據上文提及與香港空域有關的例子,我們提出的勢場是利用香港的人口數據來計算。圖
4
左邊顯示了人口分佈;而右邊則顯示了按照人口而計算的勢場。右邊顯示的排斥勢,在概念上是在各個來源中人口密度影響的疊加,並且是根據左邊顯示的人口分佈計算出來。
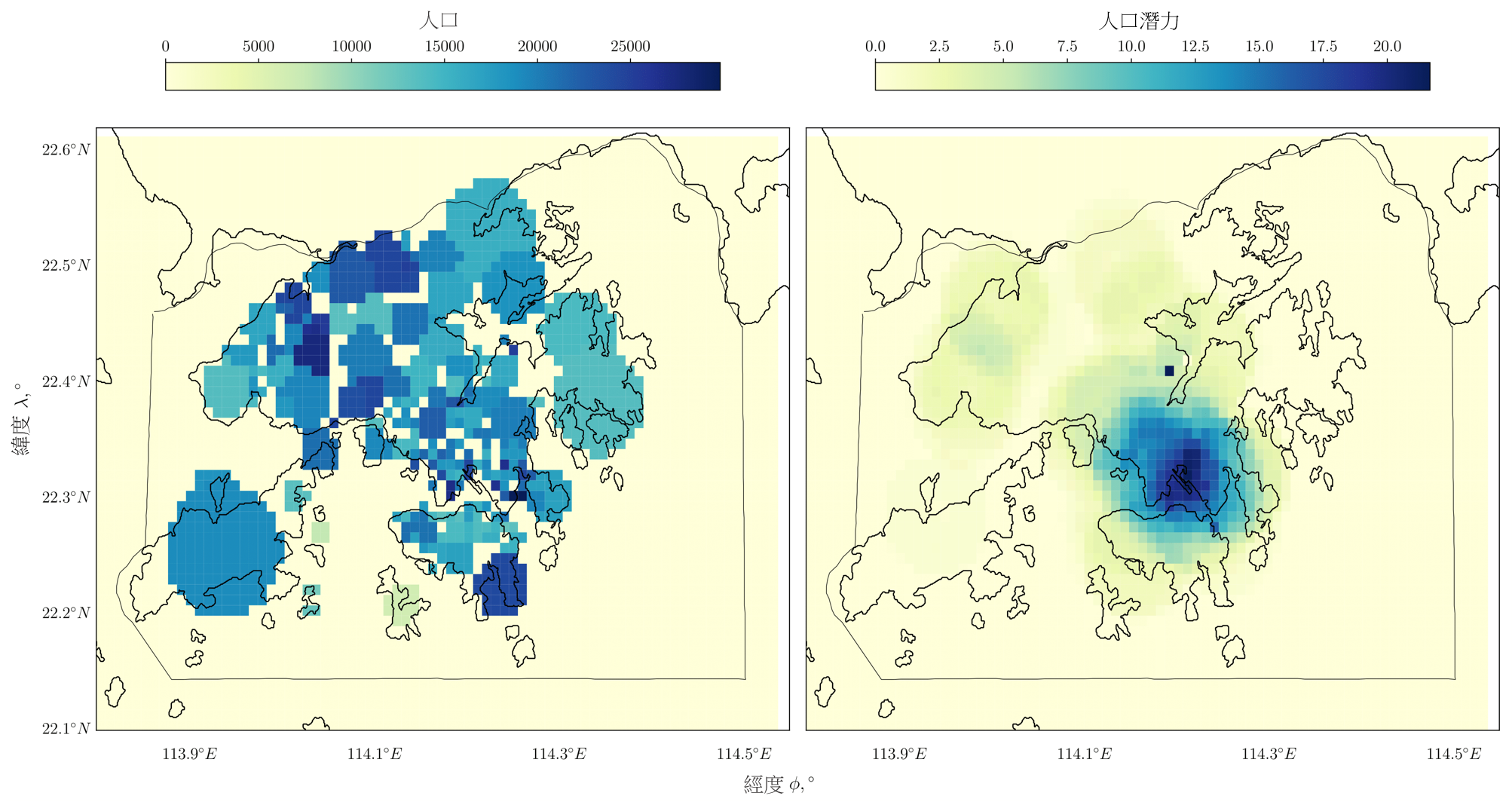
圖 4:香港的人口分佈(左)及使用公式 (9) 產生的相應勢場表示(右)。
5. 包括考量人口因素及轉向限制的後續離場階段規劃
在第 II.A.4 節說明的考量人口因素 A* 演算法中,透過公式(8)於當前節點位置得出最低代價函數 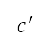 的航道,並透過測試八個方向的移動來搜尋下一個節點,如圖 5
左邊所示。這些移動方向受到網格節點的幾何配置限制,並因此可能得出不符合物理要求的航道。為了解決這個問題,我們在制定的方法中定義了一個經改良的搜尋方向,其中包含以採樣為基礎的航道規劃方法概念;圖 5 的右邊提供了一個例子。
的航道,並透過測試八個方向的移動來搜尋下一個節點,如圖 5
左邊所示。這些移動方向受到網格節點的幾何配置限制,並因此可能得出不符合物理要求的航道。為了解決這個問題,我們在制定的方法中定義了一個經改良的搜尋方向,其中包含以採樣為基礎的航道規劃方法概念;圖 5 的右邊提供了一個例子。
將 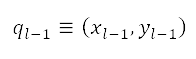 ,
, 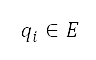 定為與航道中當前及下一個節點對應的點(以笛卡兒坐標表示)。為了增強航道的靈活性,在不同半徑
定為與航道中當前及下一個節點對應的點(以笛卡兒坐標表示)。為了增強航道的靈活性,在不同半徑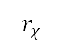 (其中
(其中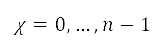 )的
)的 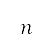 個同心圓的圓周上,我們在每一個角度區間
個同心圓的圓周上,我們在每一個角度區間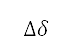 的
的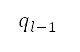 四周產生不同的樣本點。圖 5 右邊說明了這個做法,其中
四周產生不同的樣本點。圖 5 右邊說明了這個做法,其中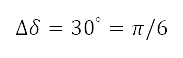 rad 及
rad 及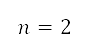 。為樣本而產生的各點位置,以笛卡兒坐標
。為樣本而產生的各點位置,以笛卡兒坐標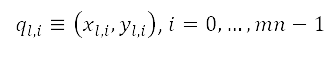 表示,計算方法如下
表示,計算方法如下
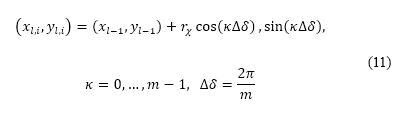
我們亦引入了一個用作限制航道角度變化的轉向懲罰,其中考慮了飛機的橫向適航性,並將這個透過抽樣得出的轉向懲罰納入到考量人口因素 A* 方法中。我們將這種改良稱為包含轉向限制的考量人口因素 A* 方法。經改良的代價函數 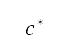 表達如下
表達如下
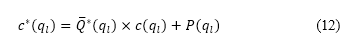
其中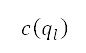 是上文提及的公式 (7) 中的代價函數,而經擴展的標準化勢
是上文提及的公式 (7) 中的代價函數,而經擴展的標準化勢 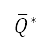 和轉向懲罰
和轉向懲罰 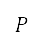 將會在下文說明。我們將
將會在下文說明。我們將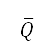 的領域(亦即在公式 (10) 中於
的領域(亦即在公式 (10) 中於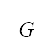 上定義的標準化排斥勢)透過與
上定義的標準化排斥勢)透過與 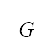 中節點
中節點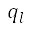 in
in 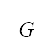 相鄰的四個點上,計算標準化勢的雙線性插值,來擴展了至
相鄰的四個點上,計算標準化勢的雙線性插值,來擴展了至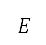 領域。我們以
領域。我們以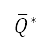 來表示這個擴展,以用來計算公式 (12) 的代價函數。
來表示這個擴展,以用來計算公式 (12) 的代價函數。
只有上一條航道和下一條航道之間的角度差 η 大於指定的角度區間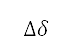 (用作圓形搜尋方向的區間)時,才應用位於
(用作圓形搜尋方向的區間)時,才應用位於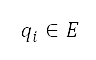 點的轉向懲罰
點的轉向懲罰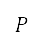 ,以避免航道角度急劇變化。懲罰權重
,以避免航道角度急劇變化。懲罰權重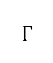 會根據起始節點到目標節點的距離加以調整。當上一個航道角度和下一個航道角度之間的差異增加時,懲罰便會增加,表達如下
會根據起始節點到目標節點的距離加以調整。當上一個航道角度和下一個航道角度之間的差異增加時,懲罰便會增加,表達如下
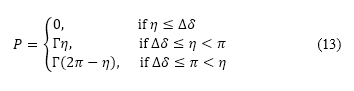
某程度上,當考慮飛機的適航性時,這個懲罰會作為一個慣性力。由公式 (12) 估算出的最低成本點,會在各個樣本點中選取為航道上的下一個節點,這個過程會一直重複,直至飛機到達目標為止。
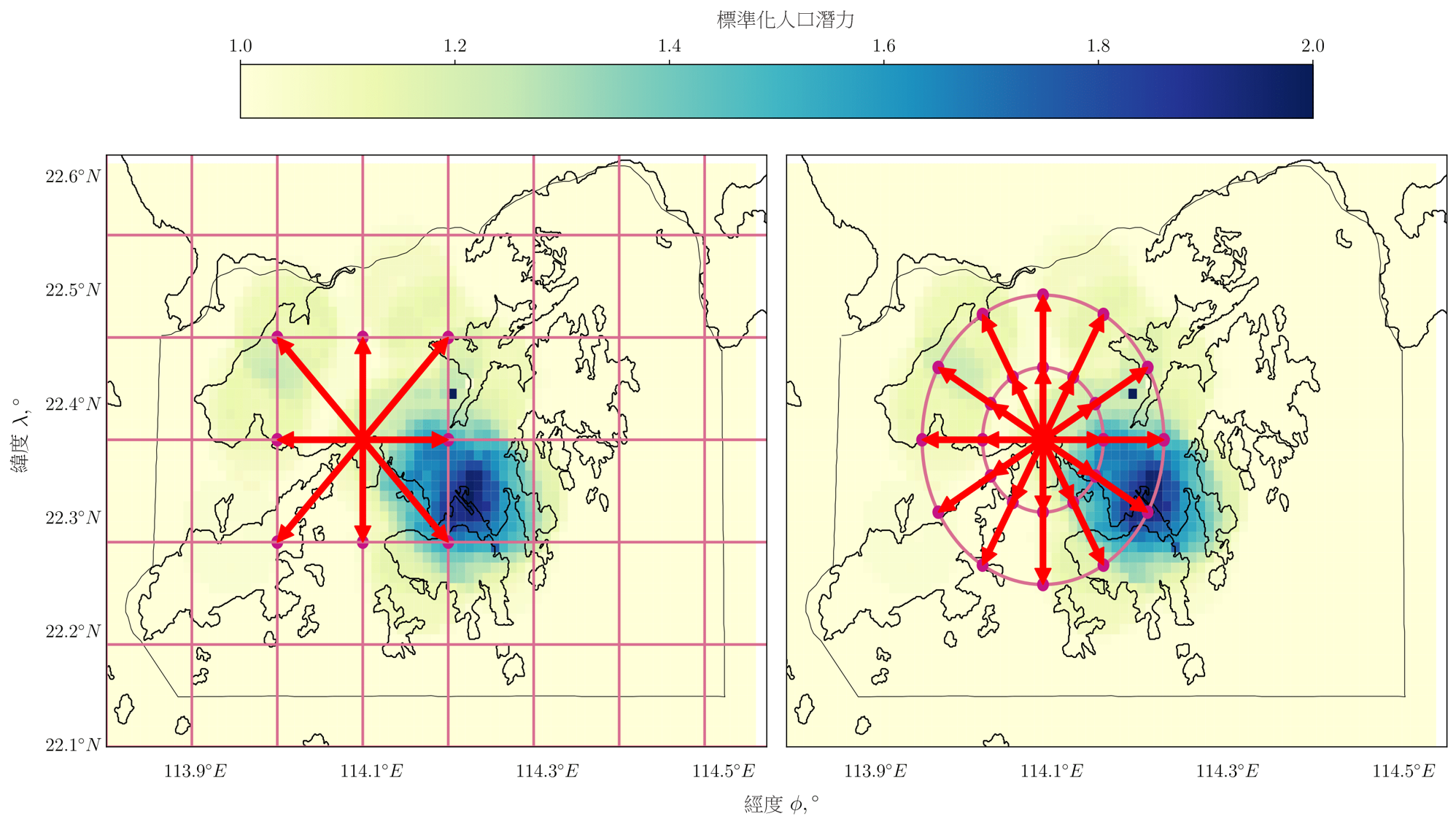
圖 5:A*演算法及考量人口因素 A* 方法在網格上的八個可能移動方向(不按比例)(左)及
在包含轉向限制方法下,考量人口因素 A* 的 24 個可能移動方向(右)
B. 高度航道規劃
第 II.A 節說明的地平面航道規劃方法,在考慮禁飛區、跑道角度、機場附近的飛機飛機間隔、人口密集地區及轉向限制下,確定了從離場機場到強制位置報告點的最短地平面航道。我們制定的高度航道規劃方法,透過估計航跡沿途的燃料消耗及累積的感知到的噪音水平,以沿著產生的地平面航道顯示出一條完整的三維航道。在第 II.B.1 節,我們提出一個能將這條航跡沿途的燃料消耗和噪音水平減到最低的優化構思。第 II.B.2 節解釋一個縱向的模擬飛行方法,以在計算相應的燃料消耗量時產生前往目標的飛行航道。第 II.B.3 節說明用作估算沿著這條飛行航道的噪音水平的方法。
1. 優化問題的構思
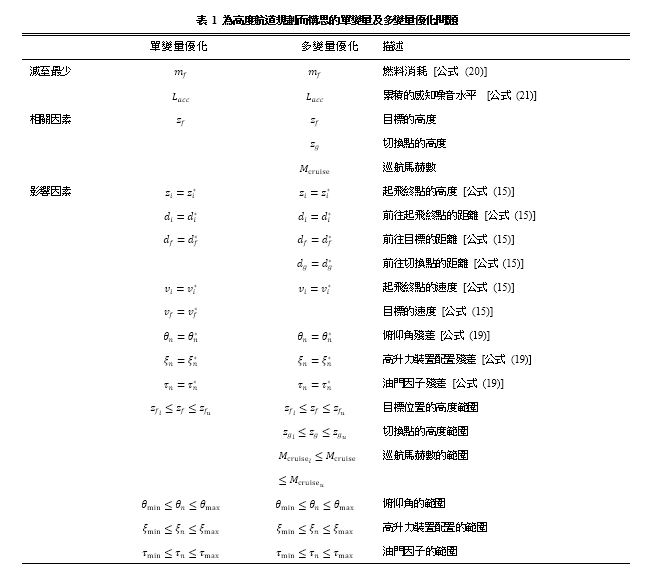
本研究提出了兩個高度航道的構思,分別是單變量優化及多變量優化,視乎沿著航道的高度上限是否改變而定。我們透過圖 6 來說明這兩個構思。舉例而言,假如有一部飛機從香港國際機場出發(在圖 6a 中以粉紅色星號標示),這部飛機必須飛過其中一個強制位置報告點(以黑色三角形標示),這是我們航道規劃方法的一個目標。根據 AIP 規定,深藍色區域的航行高度層上限為 25,000 英尺。我們使用單變量構思以規劃從香港國際機場前往這區域內報告點的航道,如 BEKOL、TAMOT 和 SIERA(如圖 6a 的藍色文字所示)。另外,我們構思了優化多變量問題,以因應從香港國際機場前往在航行高度為「地平面至無限」(AIP 所採用的術語,表示其高度不設上限,在圖 6a 中以灰色區域表示)區域上的點來規劃航道。表 1 總結了兩種構思的詳情,並會在下文加以說明。
我們假設單變量優化所產生的高度航道,是由兩個飛行航段組成:起飛及加速爬升,如圖 6b 所示。圖中的起飛和加速爬升航段,分別與地平面航道的初步及後續離場階段對應。我們透過模擬的第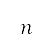 n 個時間步長來隱含地確定俯仰角
n 個時間步長來隱含地確定俯仰角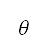 、高升力裝置的配置
、高升力裝置的配置 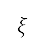 及油門因子
及油門因子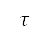 ,以及根據距離
,以及根據距離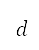 ,以及根據距離
,以及根據距離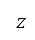 及速度
及速度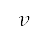 為每個航行段明確地加入邊界條件,來進行確定航道的模擬飛行(在第 II.B.2
闡述)。從地平面航道的初步及後續離場,得出到達起飛及加速爬升航段終點的距離
為每個航行段明確地加入邊界條件,來進行確定航道的模擬飛行(在第 II.B.2
闡述)。從地平面航道的初步及後續離場,得出到達起飛及加速爬升航段終點的距離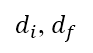 。視乎飛機類型和承載情況,在起飛終點的高度
。視乎飛機類型和承載情況,在起飛終點的高度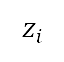 和速度
和速度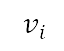 均為固定。而加速爬升終點的目標高度
均為固定。而加速爬升終點的目標高度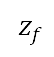 ,是單變量優化的設計變量,如表 1
第二列所示。目標高度的改變會導致與引擎動力和飛機速度等操作條件有關的垂直飛行剖面出現變化。這些條件會進一步令累積的感知到的噪音水平
,是單變量優化的設計變量,如表 1
第二列所示。目標高度的改變會導致與引擎動力和飛機速度等操作條件有關的垂直飛行剖面出現變化。這些條件會進一步令累積的感知到的噪音水平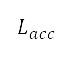 及燃料消耗量
及燃料消耗量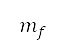 改變。因此,我們因應目標高度將燃料消耗及累積的感知到的噪音降至最低,如表 1
所示。在不同航行高度層邊界之間切換的飛行航道,透過多變量優化來模擬,如表 1 第三列所示。假設這條航道有五個航段(如圖 6c
所示):起飛、加速爬升、恆定校正空速(CAS)爬升,以及恆定馬赫數爬升和巡航。在多變量優化中的起飛航段亦與地平面航道的初步離場階段對應,而其餘航段則於地平面航道的後續離場階段對應。除了目標點的高度外,我們亦將在切換點
改變。因此,我們因應目標高度將燃料消耗及累積的感知到的噪音降至最低,如表 1
所示。在不同航行高度層邊界之間切換的飛行航道,透過多變量優化來模擬,如表 1 第三列所示。假設這條航道有五個航段(如圖 6c
所示):起飛、加速爬升、恆定校正空速(CAS)爬升,以及恆定馬赫數爬升和巡航。在多變量優化中的起飛航段亦與地平面航道的初步離場階段對應,而其餘航段則於地平面航道的後續離場階段對應。除了目標點的高度外,我們亦將在切換點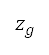 的巡航馬赫數
的巡航馬赫數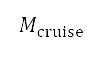 及高度視為設計變量。這個在航道上的切換點位於圖6a 中藍色與灰色區域之間的邊界,當中航行高度上限會從
25,000 英尺切換至無限。我們將這個點設定在加速爬升航段的終點,同時亦考慮了這個點的其他邊界條件(如高度、距離和速度)。如上文所述,這個點的高度是其中一個設計變量。前往這個點的距離
及高度視為設計變量。這個在航道上的切換點位於圖6a 中藍色與灰色區域之間的邊界,當中航行高度上限會從
25,000 英尺切換至無限。我們將這個點設定在加速爬升航段的終點,同時亦考慮了這個點的其他邊界條件(如高度、距離和速度)。如上文所述,這個點的高度是其中一個設計變量。前往這個點的距離 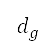 是透過 AIP 來確定的。由於加速爬升後的後續航段屬於恆定速度類型(恆定的 CAS
或馬赫數),同時巡航馬赫數是其中一個設計變量,因此在切換點的速度
是透過 AIP 來確定的。由於加速爬升後的後續航段屬於恆定速度類型(恆定的 CAS
或馬赫數),同時巡航馬赫數是其中一個設計變量,因此在切換點的速度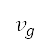 ,是按以下公式由在切換點的巡航馬赫數和高度來確定:
,是按以下公式由在切換點的巡航馬赫數和高度來確定:
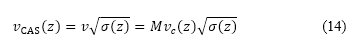
其中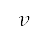 是真正的空速,
是真正的空速,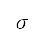 是密度比,而
是密度比,而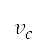 是音速。我們假設當等量空速等於校正空速
是音速。我們假設當等量空速等於校正空速 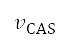 。在表 1,帶有星號的符號表示上文因應模擬飛行方法而解釋的既定邊界條件。AIP
提供了在強制位置報告點
。在表 1,帶有星號的符號表示上文因應模擬飛行方法而解釋的既定邊界條件。AIP
提供了在強制位置報告點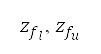 以及切換點
以及切換點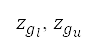 的航行高度下限及上限。巡航馬赫數的變量限制於下馬赫數和上馬赫數
的航行高度下限及上限。巡航馬赫數的變量限制於下馬赫數和上馬赫數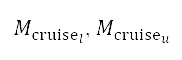 之間,是根據飛機類型及其操作條件而定。高升力裝置的配置及油門因子受限於區間
之間,是根據飛機類型及其操作條件而定。高升力裝置的配置及油門因子受限於區間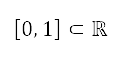 之間,
而俯仰角則受到起飛、爬升及巡航的適當操作條件所限制。用作解答這些單變量及多變量多目標優化問題的方法,是以非支配型排序基因遺傳演算法 II(NSGA-II,是一種快速分類及精良的多目標遺傳演算法)為基礎 [40]。
之間,
而俯仰角則受到起飛、爬升及巡航的適當操作條件所限制。用作解答這些單變量及多變量多目標優化問題的方法,是以非支配型排序基因遺傳演算法 II(NSGA-II,是一種快速分類及精良的多目標遺傳演算法)為基礎 [40]。
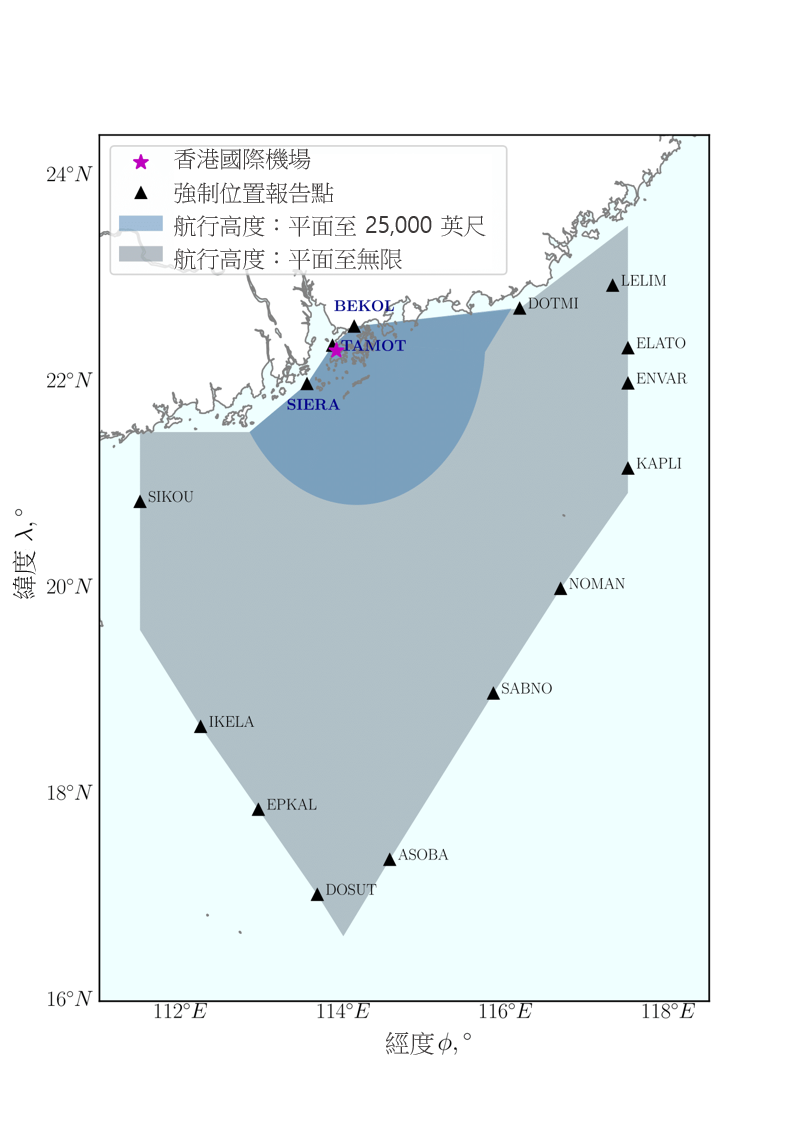 a) 香港空域的飛行高度限制
a) 香港空域的飛行高度限制
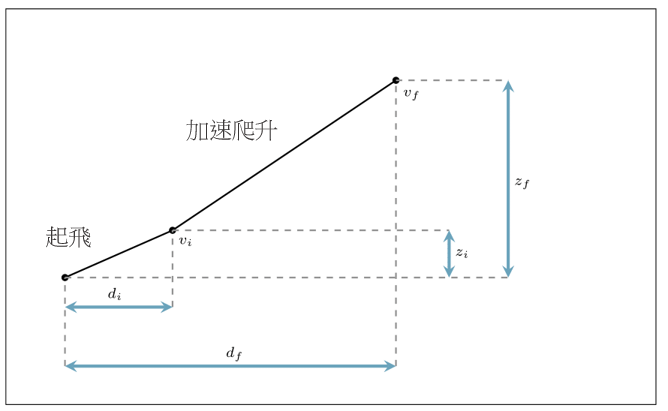 b) 單變量優化的航段(不按比例)
b) 單變量優化的航段(不按比例)
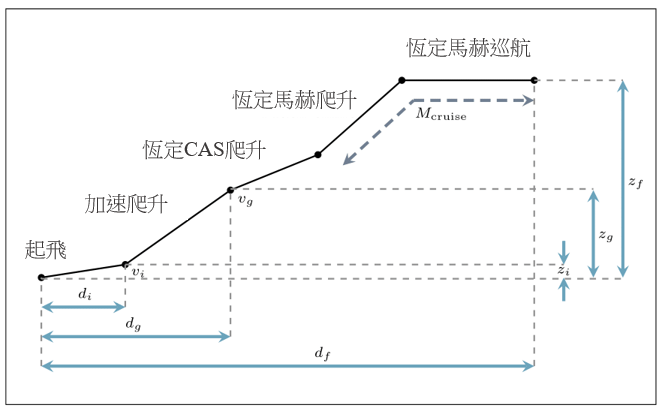 c) 多變量優化的航段(不按比例)
c) 多變量優化的航段(不按比例)
圖 6:飛行高度限制圖 a) 影響單變量及多變量優化的選擇,及航段組合以模擬單變量優化的離場航道 b) 及多變量優化 c)
這個演算法會建立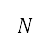 個包含設計變量的人口,並將透過交互和變異而產生的父母及後代結合起來。之後,我們會為這個人口估算目標,並且按它們的等級和擠擁距離以遞增方式排列。這個等級表示了以顯性為基礎的解答層級次序。舉例而言,在設計變量值
個包含設計變量的人口,並將透過交互和變異而產生的父母及後代結合起來。之後,我們會為這個人口估算目標,並且按它們的等級和擠擁距離以遞增方式排列。這個等級表示了以顯性為基礎的解答層級次序。舉例而言,在設計變量值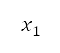 及
及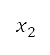 下,當
下,當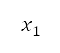 支配
支配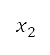 時,
時,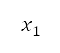 便會比
便會比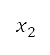 具有較高等級。在相應於
具有較高等級。在相應於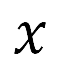 下將兩個目標
下將兩個目標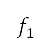 和
和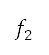 減到最低的優化問題中,其定義為
減到最低的優化問題中,其定義為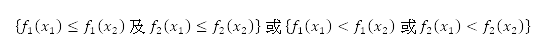 。擠擁距離表示解答的密度。假如兩個解答屬於同一等級,則位於密度較低區域的解答將獲分配較高的優先次序。排序列表的前半部分會進化成後代,並組成下一代人口
。擠擁距離表示解答的密度。假如兩個解答屬於同一等級,則位於密度較低區域的解答將獲分配較高的優先次序。排序列表的前半部分會進化成後代,並組成下一代人口
本研究採用了兩個特點以提升優化過程的計算效率。首先,有別於探索連續領域的傳統 NSGA-II,具有整數編程的 NSGA-II
會用作進行離散優化。雖然我們的設計變量是與連續的物理數量對應,但是考慮到其實際意義的離散性,則有助有效地探討設計空間。舉例來說,我們可以估算在目標巡航高度為 11,000.0 米及 11,000.1
米的噪音和燃料消耗,並在數學上得出其中一個條件較佳的結論,但對於航空運輸航線而言,這沒有實際意義。相反,我們利用相同的計算時間來估計目標高度為 11,000 米及 11,100
米的目標函數,以找出目標函數變量的概括趨勢。為了考慮具有特定區間的設計變量,我們並沒有採用離散優化中常用的二進制編碼基因演算法,相反在 NSGA-II
中使用包含隨機整數採樣的實數編碼基因演算法。當中所產生的設計變量值為整數,上下範圍處於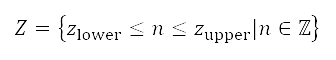 之間。由於設計變量值的數量有限,因此優化參數(例如人口規模和世代數目)會至少覆蓋 20%
的設計空間。第二,動態編碼中稱為記憶化的技術,妨礙了估算重複設計變量的解答
[41]。透過儲存燃料消耗和累積噪音的估算結果(透過進行費時的模擬飛行得出),此演算法能加快優化過程,並且在設計變量再次出現相同數值時提供已緩存的結果。
之間。由於設計變量值的數量有限,因此優化參數(例如人口規模和世代數目)會至少覆蓋 20%
的設計空間。第二,動態編碼中稱為記憶化的技術,妨礙了估算重複設計變量的解答
[41]。透過儲存燃料消耗和累積噪音的估算結果(透過進行費時的模擬飛行得出),此演算法能加快優化過程,並且在設計變量再次出現相同數值時提供已緩存的結果。
2. 燃料消耗估計量
我們採用了數據增強模擬飛行方法,以估計出高度航道沿途的燃料消耗 [42]。這個方法利用飛機初步設計階段的可用資料以及各類型飛機的歷史飛行數據,來產生縱向飛行航道以及估計燃料消耗量。早前,模擬飛行程序已根據短途、中途及長途航班的實際飛行數據加以驗證,當中近似誤差少於 7%。對於公式 (15) 中提出的移動控制公式,模擬飛行在固定邊界條件下,為飛機位置和速度作為初值的問題得出了解答:
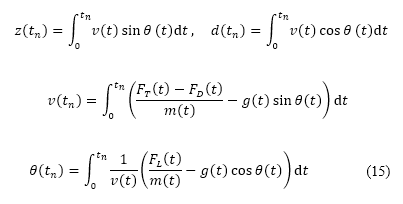
公式利用有限差值進行離散化,並在時間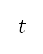 向前整合。我們將前往初步及後續離場階段終點的距離
向前整合。我們將前往初步及後續離場階段終點的距離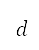 、速度
、速度 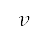 及高度
及高度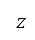 ,指定為地平面航道規劃和優化設定中的邊界條件。另外,我們亦指定了質量
,指定為地平面航道規劃和優化設定中的邊界條件。另外,我們亦指定了質量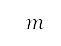 、速度、距離、高度和俯仰角的初值。之後,便使用這些初值來計算推力
、速度、距離、高度和俯仰角的初值。之後,便使用這些初值來計算推力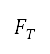 、升力
、升力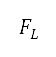 、阻力
、阻力 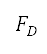 以及重力加速度
以及重力加速度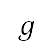 ,並將結果用來找出下一個時間步長的速度、俯仰角、距離和高度。當計算出來的速度、距離和高度符合後續離場階段終點的要求時,便終止模擬,這表示總航行時間
,並將結果用來找出下一個時間步長的速度、俯仰角、距離和高度。當計算出來的速度、距離和高度符合後續離場階段終點的要求時,便終止模擬,這表示總航行時間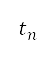 會受到邊界條件影響。具體而言,本研究所使用的推力模型透過密度比
會受到邊界條件影響。具體而言,本研究所使用的推力模型透過密度比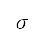 、馬赫數
、馬赫數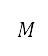 和油門因子
和油門因子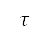 ,來考慮高度和速度的變化,如下所示
,來考慮高度和速度的變化,如下所示
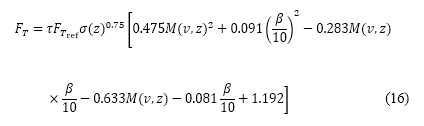
其中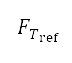 是飛機引擎的參照推力,而
是飛機引擎的參照推力,而 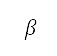 是其涵道比。所有參數均取決於引擎類型,並且假設為常數。馬赫數和密度比是速度和高度的函數:
是其涵道比。所有參數均取決於引擎類型,並且假設為常數。馬赫數和密度比是速度和高度的函數:
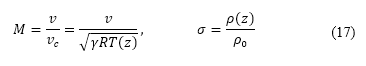
其中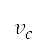 是音速,亦是空氣熱容比
是音速,亦是空氣熱容比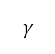 、氣體常數
、氣體常數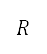 及大氣溫度
及大氣溫度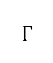 的函數。空氣密度、壓力和溫度是由國際標準大氣模型 [43] 確定。包括高度的引力加速度
的函數。空氣密度、壓力和溫度是由國際標準大氣模型 [43] 確定。包括高度的引力加速度 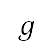 的變化,是透過地球形狀的球面近似值計算。
的變化,是透過地球形狀的球面近似值計算。
空氣動力(升力 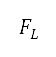 及阻力
及阻力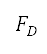 )會與空氣密度、速度、機翼面積
)會與空氣密度、速度、機翼面積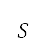 、升力系數
、升力系數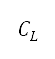 及阻力系數
及阻力系數 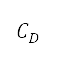 一併計算,表達如下:
一併計算,表達如下:
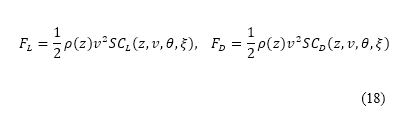
其中 表示對高升力裝置配置所作的修改。升力和阻力隱含地考慮了高度、速度、俯仰角和高升力裝置配置。特別留意的是,升力系數是由
Polhamus 公式 [44] 及 Dubs 模型 [45]
確定,作為攻角(與本研究中的俯仰角相同)、馬赫數(高度和速度的函數)、高升力裝置配置,以及其他固定的飛機資料(例如機翼展弦比、機身闊度、掠角和翼展)的外顯函數。阻力系數是由剖面阻力、觸發阻力和波浪阻力的經驗阻力累積方法來確定,作為升力系數、馬赫數及其他飛機資料(例如機翼參照面積、機翼浸潤面積、翼展、平均弦長、機身闊度、機身尾錐長度、機艙長度及機翼展弦比)的外顯函數
[46]。透過解構以下子問題,便可確定模擬中每個時間步長的俯仰角、高升力裝置配置以及油門因子的值:
表示對高升力裝置配置所作的修改。升力和阻力隱含地考慮了高度、速度、俯仰角和高升力裝置配置。特別留意的是,升力系數是由
Polhamus 公式 [44] 及 Dubs 模型 [45]
確定,作為攻角(與本研究中的俯仰角相同)、馬赫數(高度和速度的函數)、高升力裝置配置,以及其他固定的飛機資料(例如機翼展弦比、機身闊度、掠角和翼展)的外顯函數。阻力系數是由剖面阻力、觸發阻力和波浪阻力的經驗阻力累積方法來確定,作為升力系數、馬赫數及其他飛機資料(例如機翼參照面積、機翼浸潤面積、翼展、平均弦長、機身闊度、機身尾錐長度、機艙長度及機翼展弦比)的外顯函數
[46]。透過解構以下子問題,便可確定模擬中每個時間步長的俯仰角、高升力裝置配置以及油門因子的值:
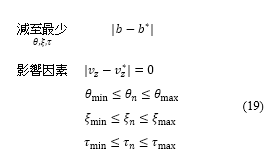
其中目標函數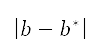 中的變量
中的變量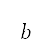 的類型取決於航段類型:起飛和加速爬升航段時,變量
的類型取決於航段類型:起飛和加速爬升航段時,變量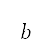 是
是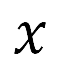 方向加速度;恆定 CAS 爬升航段時,變量
方向加速度;恆定 CAS 爬升航段時,變量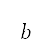 為校正空速;恆定馬赫爬升及巡航段時,變量
為校正空速;恆定馬赫爬升及巡航段時,變量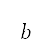 為馬赫數。而
為馬赫數。而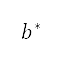 是與每個屬性對應的所需值,是由邊界條件隱含地確定。因此,將
是與每個屬性對應的所需值,是由邊界條件隱含地確定。因此,將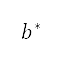 和
和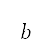 之間的絕對差異減至最少,會迫使屬性在相應的航段中保持為常數。同樣地,對每個航段而言,垂直速度
之間的絕對差異減至最少,會迫使屬性在相應的航段中保持為常數。同樣地,對每個航段而言,垂直速度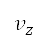 亦是一個常數,而目標垂直速度
亦是一個常數,而目標垂直速度 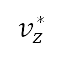 則由 [42]
所展示的數據分析來確定。每個設計變量都受限於其各自的最小值和最大值,在變量範圍內用下標「min」和「max」表示,並會因航段類型而各有不同。我們只會在起飛和加速航段(期間會展開襟翼和縫翼)中,考慮高升力裝置配置。
則由 [42]
所展示的數據分析來確定。每個設計變量都受限於其各自的最小值和最大值,在變量範圍內用下標「min」和「max」表示,並會因航段類型而各有不同。我們只會在起飛和加速航段(期間會展開襟翼和縫翼)中,考慮高升力裝置配置。
燃料消耗量是採用以下公式的離散形式計算
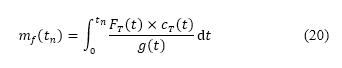
這取決於模擬中每個時間步長的推力、重力加速度及具體的燃料消耗量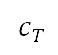 。具體燃料消耗量是使用從引擎數據集(透過開源資料庫Surrogate Modelling
Toolbox(SMT)[47]
取得)所建立的代理模型來確定的,並視乎高度、速度和油門因子而定。
。具體燃料消耗量是使用從引擎數據集(透過開源資料庫Surrogate Modelling
Toolbox(SMT)[47]
取得)所建立的代理模型來確定的,並視乎高度、速度和油門因子而定。
3. 累積感知到的噪音水平估計
我們使用了 Eurocontrol 飛機噪音及性能(ANP)數據庫‡‡中的噪音動力距離(NPD)表來估算累積感知到的噪音水平。ANP/NPD 數據庫是一個網上數據資源,用作估計由飛機所觸發的噪音影響,當中展示了各種不同的飛機類型、操作和聲學模型,並且提供了 ECAC Doc. 29 及 ICAO Doc. 9911 指導文件 [48,49]。
針對感知到的噪音水平,我們使用了 ANP 數據庫中的 A
加權聲曝水平模型,它代表了在一秒之內整合的總聲音能量,是按照人類耳朵的靈敏度而專門配置,並且會受到飛機類型、引擎推力、操作模式(例如離場或進場)以及飛機與觀察者之間的距離所影響
[50]。為航道規劃而選擇的飛機將類型定為常數。另外,由於我們在本研究中只考慮離場航道規劃,因此操作模式亦是一個常數。引擎推力和距離以第 II.B.2
節中說明的模擬飛行來確定。在我們的研究中,由於是假設觀察者是處於飛機下方海平面的地面上;因此與觀察者之間的距離相等於高度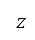 。高度航道沿途的累積感知到的噪音水平,可從以下表達式得出:
。高度航道沿途的累積感知到的噪音水平,可從以下表達式得出:
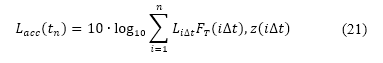
其中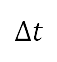 是模擬飛行中使用的時間步長,如第 II.B.2 節所述,而
是模擬飛行中使用的時間步長,如第 II.B.2 節所述,而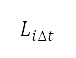 是第
是第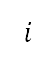 個時間步長的 A 加權聲曝水平 。由於累積的聲曝水平顯著受到對數和所導致的最大
個時間步長的 A 加權聲曝水平 。由於累積的聲曝水平顯著受到對數和所導致的最大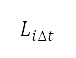 所影響,因此我們在優化過程中只考慮爬升航段的聲曝水平,從而能清晰地觀察改變高度航道對累積噪音水平所產生的影響。
所影響,因此我們在優化過程中只考慮爬升航段的聲曝水平,從而能清晰地觀察改變高度航道對累積噪音水平所產生的影響。
III. 結果及討論
本節說明地平面航道規劃的結果,以及沿著香港至倫敦及香港至台北(本文所採用的兩個研究個案)這兩條航線所得出的一組最佳高度航道。模擬飛行的參數是以配備了 GE90-115B 引擎的波音 777-300ER 客機為依據。第 II 節說明由我們制定的航道規劃和優化過程,適用於從香港國際機場(北緯 22°18'32.0'',東經 113°54'52.0'')越過強制性 ATS 位置報告點的航班,即前往倫敦希斯路機場的飛機為 BEKOL (北緯 22°32’36.0’’,東經 114°08’00.0’’);前往台灣桃園國際機場為 ENVAR(北緯21°59’29.8’’N,東經 117°30’00.0’’)。
A. 地平面航道規劃
在本節,我們採用第 II A 節中的方法,為香港至倫敦的航線(圖 7)及香港至台北的航線(圖 8)產生經優化的地平面航道。在討論每條航線的具體結果前,我們會先描述圖中所包括的標示方式。
圖中的位置與香港國際機場對應,並以星號標示,當中香港國際機場是航道規劃的起點。以黑色三角形標示的地點是強制性 ATS 位置報告點,是航道規劃的目標點。以紅色標示的區域是第 II.A.2 節所述的障礙物,飛機無法越過。黑線代表國家的邊界及其海岸線。疊加的顏色代表標準化人口勢場的強度。如第 II.A.4 節所述,深藍色區域的人口密度高,不適合飛機飛越。相應的 SID 路徑以粗灰線顯示,與使用黑色輪廓圓圈標示的 SID 引導點連接。另外,以波音 777-300ER 航班的快速存取記錄器(QAR)數據所產生的九條飛行航道,以紫色線顯示。QAR 記錄了飛機在飛行過程中的詳細操作資料,例如位置、高度角、空速、重量等。在本研究中,QAR 數據中的經度、緯度、壓力高度、推力及重量資料會用作比較和驗證。航道規劃結果會用四種顏色表示,以橙色顯示的Dubins航道,是初步離場階段(如第 II.A.3 所述)所產生的航道,亦是三條後續離場航道的共用航道。這三條航道的規劃,即從Dubins航道終點至目標開始,會以「A*」、 「population-aware A*」及「population-aware A* with steering constraints」的名稱表示。從這裡起,為了方便易讀,我們將這三種方法分別稱為 A*、PA* 及 PA*S。
以藍色顯示的 A* 航道,是採用 A* 演算法得出的結果,當中只考慮第 II.A.2 節中提及的障礙物限制,並透過使用在公式 (7) 中表達的代價函數來產生這條航道。以綠色顯示的PA* 航道,是採用第 II.A.4 節中提到的人口密集地區限制以及障礙物限制而得出的結果,並透過使用在公式 (8) 中表達的代價函數來產生這條航道。以洋紅色表示的 PA*S 航道,是除了障礙物及人口密集地區限制外,亦採用了轉向懲罰考慮因素而得出的結果,並透過使用在公式 (12) 中表達的代價函數來產生這條航道。PA*S 航道代表了本文所制定的地平面航道規劃方法,當中在考慮到飛機的適航性及轉向懲罰下,找出避開障礙物和人口密集地區的最短航道。
1.香港至倫敦
圖 7 展示了飛機從香港國際機場起飛並前往倫敦希斯路機場的地平面航道規劃。這條航線會越過由香港 AIS 指定的強制性 ATS 位置報告點 BEKOL。根據 BEKOL 的位置,我們選擇圖 2 中所示的 Departure 07R-1,作為這次模擬的初步離場航道。相對於飛往 BEKOL 的飛機,這個選擇亦與我們對大部分 QAR 飛行航道數據的觀察結果一致。使用 Departure 07R-1 至 BEKOL 的 SID 路徑,是以連接 HKIA–ROVER–TUNG LUNG–ATENA–BEKOL 的線來表示。從香港國際機場開始的初步離場階段,會在 ROVER 及 TUNG LUNG 線上的一個點結束。我們選擇這個靠近人口密集地區作為結束點,目的是要觀察透過不同規劃方法所產生的航道會出現什麼變化。後續離場階段與從這點至 BEKOL 的航段對應。我們發現所產生的Dubins航道能符合初步離場航道限制,並且避開了機場四周的障礙物。
之後,在不考慮人口情況下 A* 演算法得出了越過香港內陸人口密集地區的最短航道。相反,PA* 和 PA*S 方法所產生的航線,避開了這個具有高度標準化人口勢場的區域。在航道規劃上,由於以笛卡兒坐標表示的 PA*S 比 PA* (只在網格點上運作)有更大自由度,因此當包含轉向限制時,可觀察到航向方向出現較小的急劇變化。
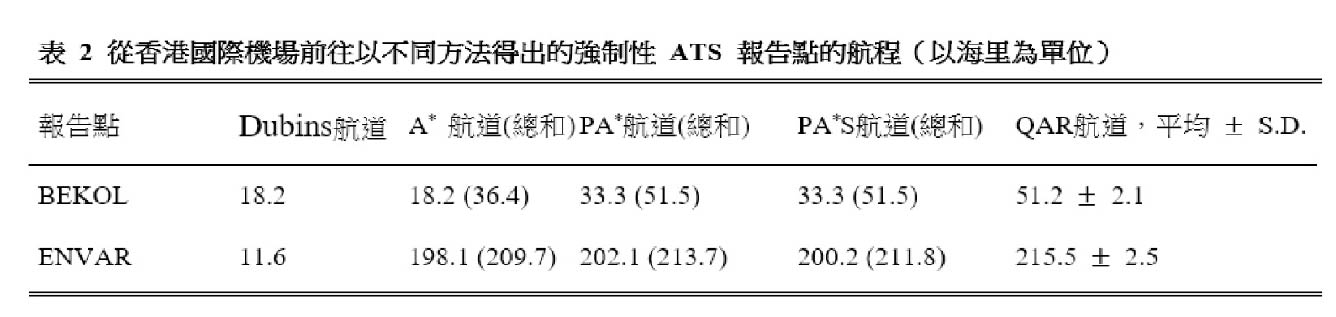
在三個結果中,包含Dubins航道的 PA*S 與 SID 路徑及 QAR 航道最為相似,尤其是初步離場航道幾乎與 SID 路徑及 QAR 航道相同。從香港國際機場至 ROVER,被跑道角度限制的Dubins航道,幾乎與 SID 路徑和 QAR 航道平行。QAR 航道偏離Dubins航道以及 ROVER 和 TUNG LUNG 之間的 SID 路徑,飛越人口密集的地區,並最終在 ATENA 越過香港東面的邊陲地帶飛往 BEKOL。當轉向更接近 SID 引導點 TUNG LUNG 飛往 ATENA 時,與 QAR 航道比較下 PA* 航道更接近 SID 路徑,顯示我們所制定的方法有助於 SID 的規劃。除了這個相似之處,可飛性亦可以由 PA*S 航道的初步及最終航道角來確定。在 TUNG LUNG 四周的初步航道角,由於按照著初步離場階段終點的角度,因此航道穩定地朝向目標移動。在 BEKOL 附近,後續離場階段終點的最終航道角與 QAR 航道的航道角相似,在作為驗證上代表一條在物理上可飛行的航線。表 2 展示了透過每種航道規劃方法而計算得出的航道長度,其中第一列表示在初步離場階段中從Dubins航道計算得出的距離。隨後三列代表使用本文提出的航道規劃方法,在後續離場階段計算得出的距離。在這些列中,括號「(總和)」中的航道長度是指在初步及後續離場階段飛機所飛行的總距離,這是將透過從Dubins航道為這條航線得出的相應距離,與從每種方法得出的後續離場航道距離相加而計算出來。至於圖 7 所示的九個 QAR 航道長度,最後一列顯示了它們的平均值和標準偏差(S.D.)。為了評估我們的結果,我們將 A*、PA* 和 PA*S 航道的總長度,與 QAR 航道的平均長度進行比較。在這個個案中, QAR 航道的平均長度(51.2 海里)比 PA*S 航道的總長度(51.5 海里)短 0.3 海里。然而,值得留意的是 QAR 航道越過人口潛力高,而不是潛力低的地區。因此,PA*S 航道提供了一個經改良的解決方案,其中可避開人口密集的地區,因此在無需顯著增加飛行距離之下,或有助降低噪音的影響。
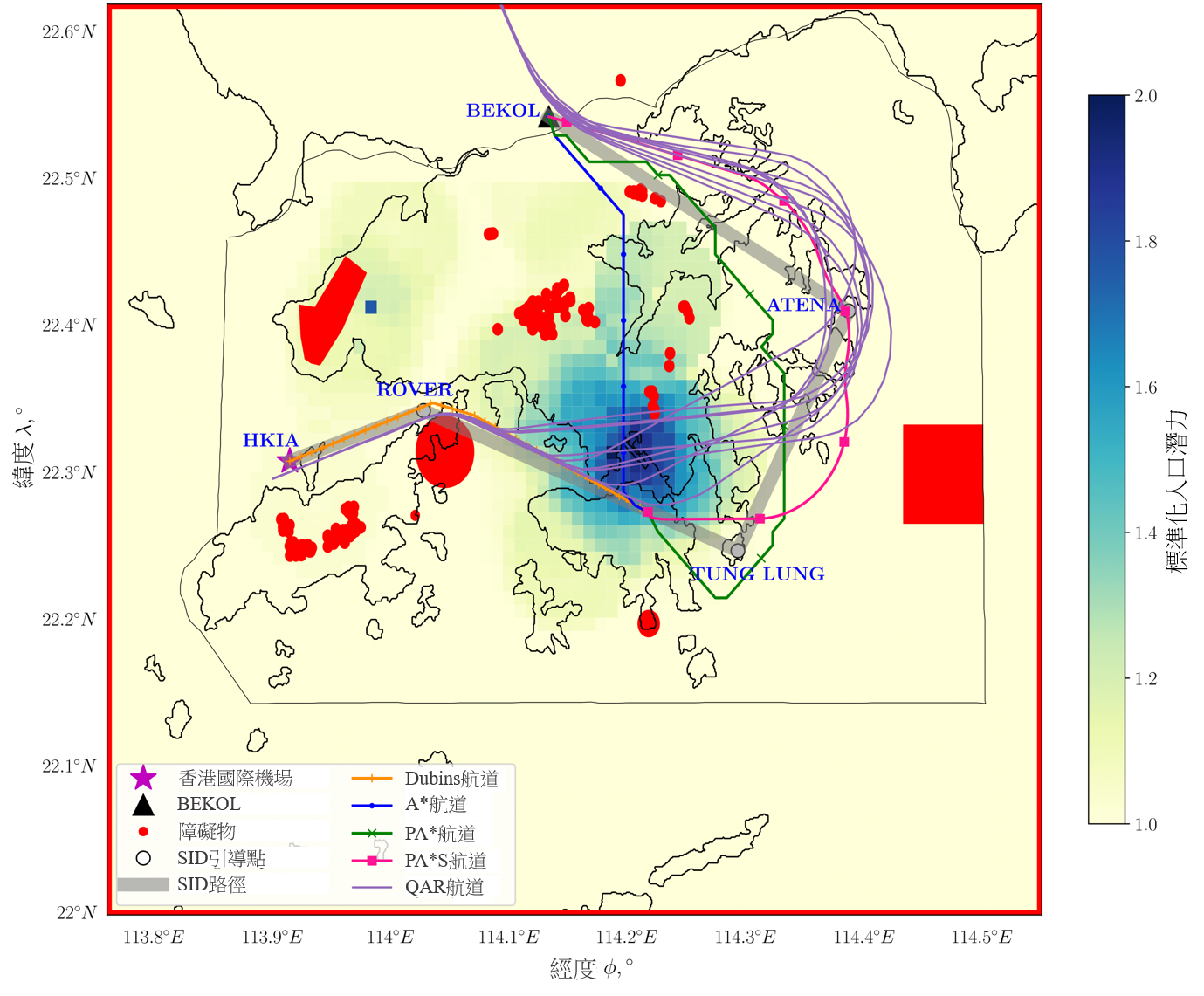
圖 7:從香港國際機場至 BEKOL(香港至倫敦航線)的地平面航道,其中包含障礙物及香港空域下的標準化人口潛力
2. 香港至台北
圖 8 展示了飛機從香港國際機場起飛前往台灣桃園國際機場的地平面航道規劃。這條航線會越過同樣是由香港 AIS 指定的強制性 ATS 位置報告點 ENVAR。由於目標點位於遠離香港東南面的位置,因此我們將圖 8 左邊的圖放大,而以香港地域為中心的圖則在右邊顯示。飛往 ENVAR 的 SID 路徑同樣以灰色線顯示,連接著 HKIA-ROVER-ROBBE-RAMEN-OCEAN-ENVAR。飛機的初步離場階段是從香港國際機場飛往 ROBBE,使航道規劃方法變得較為靈活,讓其可沿著Departure 07R-1 或 07R-2 移動(見圖 2)。後續離場階段將從 ROBBE 移動至 ENVAR。在右邊的放大圖中,Dubins航道幾乎與 SID 路徑和 QAR 航道平行,符合初步離場航道的限制。之後,A* 演算法產生出一條與 Departure 07R-1 路徑相似,並且越過高人口潛力地區的航道。相反,PA* 和 PA*S 方法則產生出與 Departure 07R-2 路徑相似,並且傾向避開高人口地區的航線。
最短的 A* 航道仍然會沿著 Departure 07R-1 路徑越過高人口潛力的地區。大約 70% 的 QAR 航道亦會越過這個區域,在噪音方面造成負面影響。餘下跟隨 Departure 07R-2 路徑的 QAR 航道,則與 PA*S 和 SID 路徑頗為相似。PA*S 航道在 RAMEN 和 OCEAN 之間偏離 SID 路徑,如圖中左邊所示。這個偏差特別有助縮短航道的長度,如表 2 所示。對於這條航線,QAR 航道的平均飛行距離比 PA*S 航道的平均飛行距離長約 3 海里。這個差異主要是由於在 OCEAN 四周的大幅度轉彎而造成,如圖 8 所示。我們觀察到部分 QAR 航道沒有經過 OCEAN,導致航道與 PA*S 的航道相似。這個觀察結果顯示所產生的 PA*S 航道適合飛行。雖然我們的方法所產生的航線比大部分 QAR 航道短,但是卻沒有考慮某些航空運輸的限制,例如包括有多架飛機在相似航線上飛行的空中交通情況。然而,有別於 PA*,PA*S 在 ROBBE 保持飛行方向,原因是轉向限制的作用就如慣性力般,因此亦可以模擬當前的飛行操作,如 QAR 航道所示。此外,我們在受網格點限制的 A* 及 PA* 航道中所看到的急劇轉彎,卻未有在 PA*S 航道中發現。
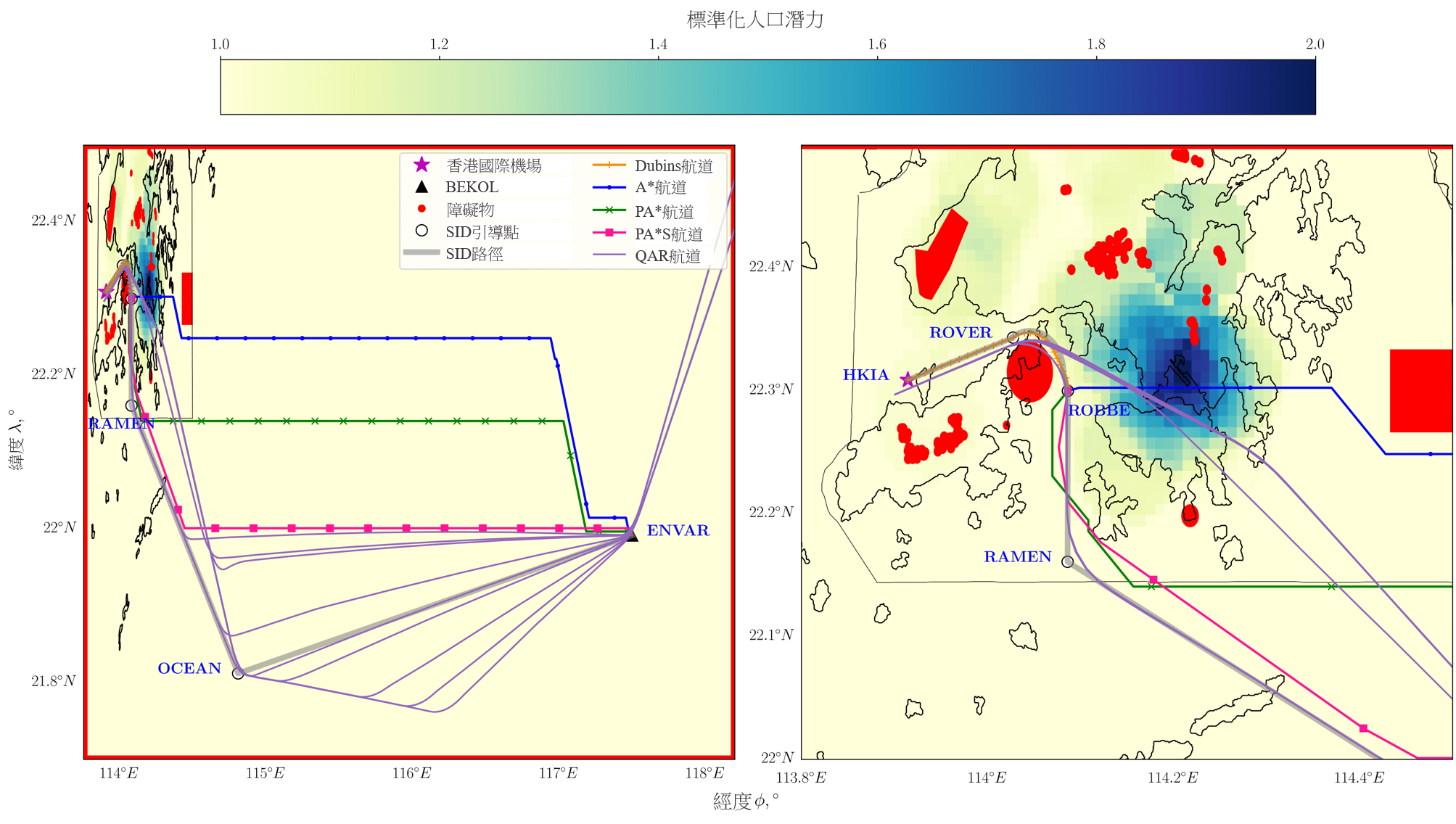
圖 8: 從香港國際機場至 ENVAR(香港至台北航線)的地平面航道,其中包含障礙物及香港空域下的標準化人口潛力
B. 高度航道規劃
我們透過進行低燃耗及低噪音影響的多目標優化,提出了在兩種情境下的高度航道,如第 III.A 節所示。按照第 II.B. 節所描述的構思,從香港國際機場到 BEKOL 的航道,是透過單變量優化得出;而從香港國際機場到 ENVAR 的航道,則是以多變量優化取得。與意在規劃出一條最短路徑的地平面航道規劃方法不同,我們希望能得出以多條高度航道作為多目標優化的一組解決方案。這些航道由圖 9 左邊和圖 10 頂部的圖表表示,其中橫軸是飛行距離,縱軸是高度。圖 9 右邊和圖 10 底部顯示了優化的可行區域,以及低燃料消耗和低累積感知到的噪音水平的帕累托前沿。可行區域是指在優化過程中,由經修改的 NSGA-II 演算法所估算的所有解決方案。在圖 9 中,這個區域以彩色地圖顯示,代表單變量優化的高度,而圖 10 則以淺藍色表示多變量優化。請留意,我們使用相同的顏色來標示圖 9 右邊優化解決方案的相應高度。在各個可行的解決方案中,非支配解決方案(即帕累托前沿)以實心的洋紅色線和三角形表示。與地平面航道圖一樣,QAR 航道的高度變化以紫色虛線和紫色星號表示。圖 9 左邊和圖 10 頂部的紫色星號,表示在各自航道中與相應的強制性 ATS 位置報告點最接近的點,而圖 9 右邊分別表示用作與解決方案進行比較的燃料消耗和噪音水平。
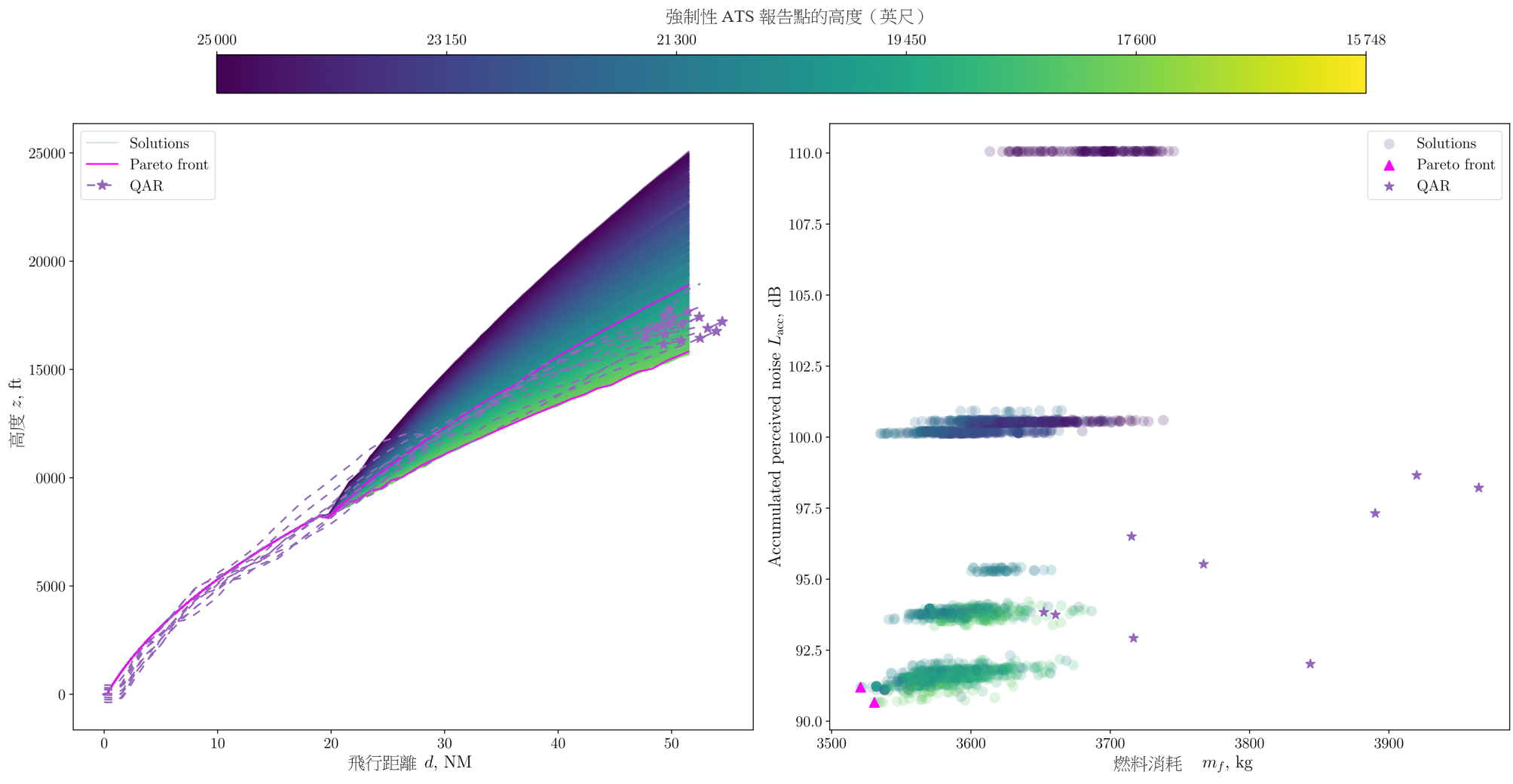
圖 9:高度航道優化的可行解決方案、其帕累托前沿,以及從香港國際機場飛往 BEKOL 的 QAR 數據(左)
及相應的燃料消耗及漸強的感知噪音水平(右)
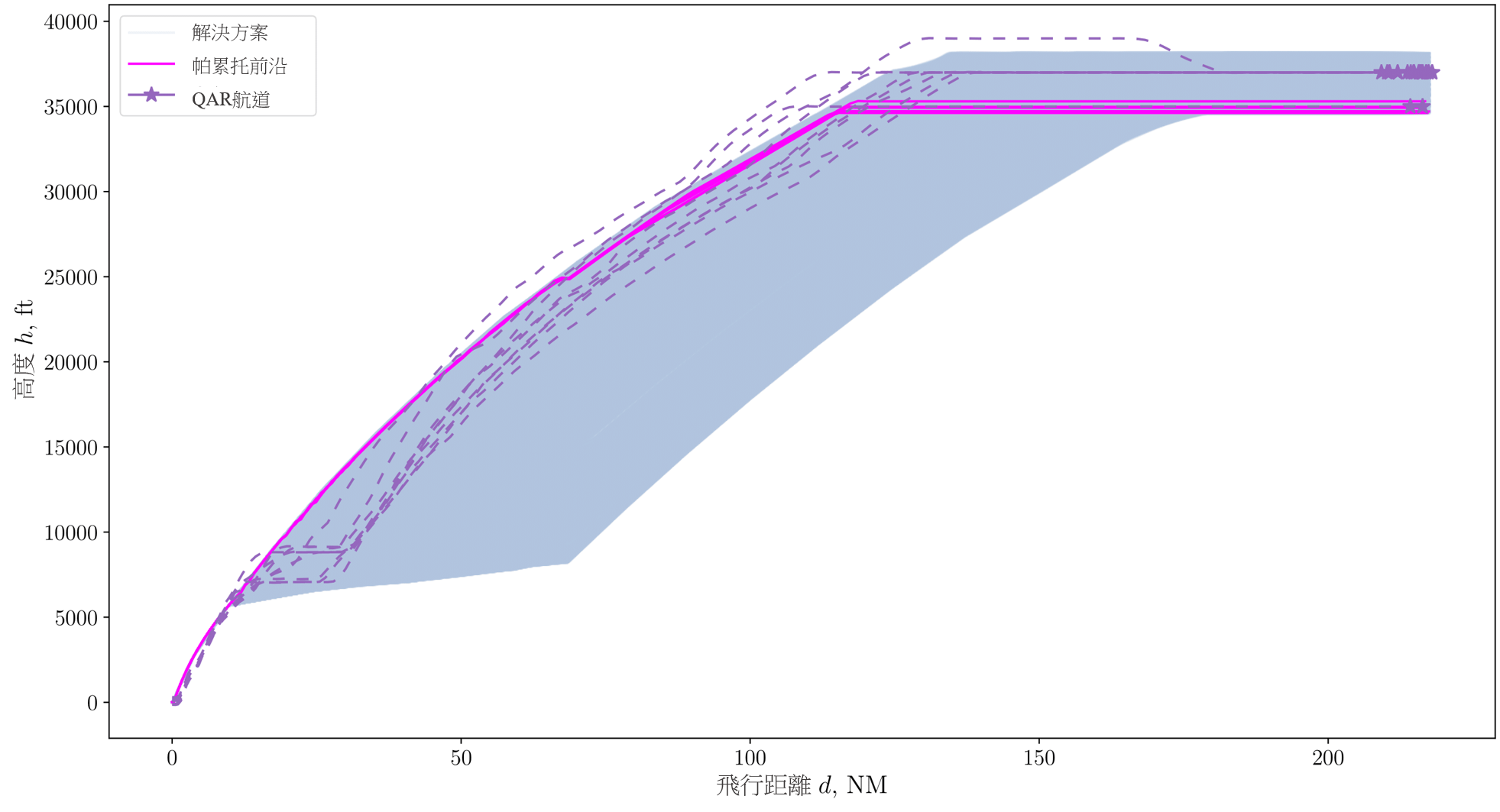
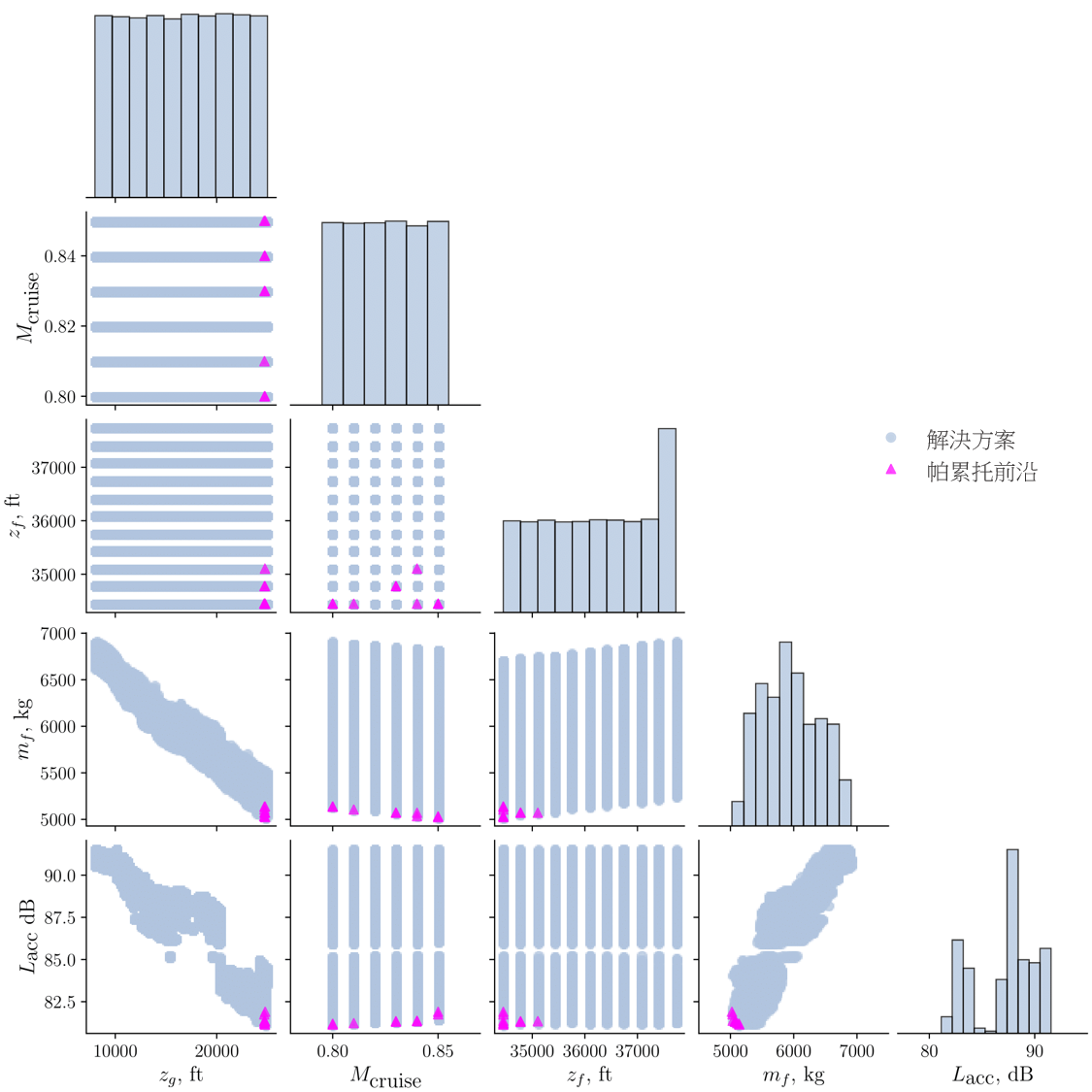
圖 10:優化高度航道的可行解決方案、其帕累托前沿,以及從香港國際機場飛往 ENVAR 的 QAR 數據(上)及
與三個設計變量相關的燃料消耗和累積感知噪音水平,即目標高度、切換點高度及巡航馬赫數(底)
高度航道由初步及後續離場航道組成,與地平面航道相似。圖 9 左邊及圖 10 頂部只有一條洋紅色線的航道,是與圖 6b 及 6c
的起飛航段對應的初步離場航道,這是與地平面航道規劃的Dubins航道部分對應。Dubins航道的飛行距離(如表 2 第二列所示),是起飛航段起點到終點的總距離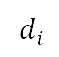 。後續離場航道的飛行距離
。後續離場航道的飛行距離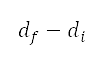 是 PA*S 航道的飛行距離,如表 2 第五列所示。我們將前往切換點
是 PA*S 航道的飛行距離,如表 2 第五列所示。我們將前往切換點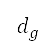 的飛行距離設定為 66 海里,這是從地平面航道規劃及 AIP 中的資料中得出。
的飛行距離設定為 66 海里,這是從地平面航道規劃及 AIP 中的資料中得出。
表 3 列出了我們使用的優化參數。在 NSGA-II 中基因演算法的世代數目和人口大小,是根據設計變量的數目及其範圍內的數值數量(根據訂明的區間而定)所確定的設計空間大小來設定的。對於單變量優化,BEKOL
目標高度的下限及上限設定為 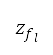 = 4,800 米 = 15,750 英尺,及
= 4,800 米 = 15,750 英尺,及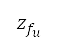 = 7,620 米 = 25,000 英尺(從 AIP 中取得)。優化以世代進化為 100 及人口大小為
20
進行,從中所產生的 2,000 個估計點,能夠覆蓋大部分設計空間,合共包含 2,821 個點。因此,我們認為世代數目和人口大小足以能具體地進行有關優化。至於多變量優化,ENVAR
的目標高度範圍剛好是巡航高度,並設定為
= 7,620 米 = 25,000 英尺(從 AIP 中取得)。優化以世代進化為 100 及人口大小為
20
進行,從中所產生的 2,000 個估計點,能夠覆蓋大部分設計空間,合共包含 2,821 個點。因此,我們認為世代數目和人口大小足以能具體地進行有關優化。至於多變量優化,ENVAR
的目標高度範圍剛好是巡航高度,並設定為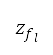 = 10,500 米 = 34,450 英尺,及
= 10,500 米 = 34,450 英尺,及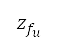 = 11,500 米 = 37,730
英尺,這是根據本研究中特定飛機類型的典型巡航高度而選擇。這個高度範圍與我們對飛行數據的觀察結果一致。巡航高度範圍的離散化區間設定為100 米,從而以較低的計算成本來估算設計空間的趨勢。巡航馬赫數
= 11,500 米 = 37,730
英尺,這是根據本研究中特定飛機類型的典型巡航高度而選擇。這個高度範圍與我們對飛行數據的觀察結果一致。巡航高度範圍的離散化區間設定為100 米,從而以較低的計算成本來估算設計空間的趨勢。巡航馬赫數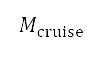 的範圍,亦是根據我們在本研究中所選飛機的運作特性而設定:
的範圍,亦是根據我們在本研究中所選飛機的運作特性而設定: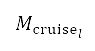 = 0.80 及
= 0.80 及 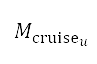 = 0.85。馬赫數的離散化區間為
0.01。雖然在這些範圍內的馬赫數並非此離散化的整數,但是針對優化的設計變量抽樣程序,我們將它們縮放成 80 至 85 之間的整數,其中的區間為 1,以能夠進行整數編碼。優化循環內的模擬飛行將這些整數設計變量,轉換成介乎
0.80
和 0.85 之間,區間為 0.01 的適當物理數值。切換點
= 0.85。馬赫數的離散化區間為
0.01。雖然在這些範圍內的馬赫數並非此離散化的整數,但是針對優化的設計變量抽樣程序,我們將它們縮放成 80 至 85 之間的整數,其中的區間為 1,以能夠進行整數編碼。優化循環內的模擬飛行將這些整數設計變量,轉換成介乎
0.80
和 0.85 之間,區間為 0.01 的適當物理數值。切換點 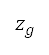 的高度範圍設定為
的高度範圍設定為 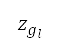 = 2,439 米 = 8,000 英尺,及
= 2,439 米 = 8,000 英尺,及 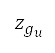 = 7,620 米 = 25,000 英尺。切換點高度變化的離散化區間為 1 米。多變量優化以世代進化為
700
及人口大小為 100 進行,覆蓋20% 的設計空間,合共 342,012 個估算點。我們測試和調整了 NSGA-II 中的突變率和交互率,以適合進行本文所提出的優化。
= 7,620 米 = 25,000 英尺。切換點高度變化的離散化區間為 1 米。多變量優化以世代進化為
700
及人口大小為 100 進行,覆蓋20% 的設計空間,合共 342,012 個估算點。我們測試和調整了 NSGA-II 中的突變率和交互率,以適合進行本文所提出的優化。

1. 香港至倫敦
圖 9 左邊顯示了從香港國際機場至 BEKOL 的高度航道,並與在右邊顯示的燃料消耗及累積感知到的噪音水平對應。這裡的累積噪音水平僅與第 II.B.3 節中提到的爬升航段對應。飛機的起飛重量設定為 3XX,XXX 公斤(根據與航空公司合作夥伴的協議,在出於保密原因下我們將數字屏蔽),這是根據 QAR 數據而得出的平均值。透過與本研究所使用的 QAR 數據進行比較,我們驗證了燃料消耗及累積感知到的噪音水平的計算模型,其中燃料消耗和累積感知到的噪音水平的相對誤差分別為 4.10% 和 2.34%,這為本研究所進行的優化帶來充分的準確性。
如圖 9 左邊所示,在起飛和加速爬升航段結束時,結果符合地平面航道規劃中Dubins和 PA*S 航道的飛行距離(如表 2 所示)。當中所產生的高度航道,其航跡與 QAR 航道非常相似。在右邊,燃料消耗及感知到的噪音水平值的分佈以顏色編碼圓圈表示,作為模擬結果(亦即從 NSGA-II 優化產生的解決方案),而 QAR 航道的相關分佈則以紫色星號顯示。在與 QAR 航道相比下,高度航道圖顯示與模擬結果對應的高度顯著地分佈得更為廣闊。然而,值得留意的是,正如在 QAR 航道的終點所觀察的一樣,在實際飛行中前往 BEKOL 的總距離與模擬結果有所分別。雖然 QAR 航道的分佈更靠近右邊,顯示有較多的燃料消耗,但是模擬結果得出的顯著高度變化以及 QAR 航道的飛行距離變化,卻得出了相似的燃料消耗分佈範圍(約為 300 公斤)。
表 4 顯示了與圖 9 右邊帕累托前沿集對應的 ATS 位置報告點的高度,以及對應的燃料消耗和累積的感知到的噪音水平。將噪音減到最低的航道目標高度為 15,458 英尺,在圖 9 右邊以洋紅色的底部三角形表示。圖 9 左邊顯示了相應的航道,其最終高度比 QAR 航道的高度低。將燃料消耗減到最低的航道目標高度為 18,917 英尺,在圖 9 右邊以洋紅色的靠左三角形表示。圖 9 左邊顯示了相應的航道,其最終高度高於QAR 航道的高度。噪音水平方面,我們觀察到在一般情況下,隨著右圖縱軸的值增加,顏色會從黃色變成深藍色,這表示隨著目標高度增加,噪音水平亦會增加。
這個趨勢是由於爬升到更高的目標高度需要更大的引擎動力輸出而造成的,並且會相應地影響感知到的的噪音水平。然而,當目標高度大約為 16,400 英尺時,這個趨勢便會逆轉,其中在一組黃色圓圈下方噪音最低點附近,可以觀察到一組綠色圓圈。對於這個特定區域的航道(即噪音趨勢逆轉的區域),飛機增加升力以到達更高的高度並非透過增強引擎動力,而是透過調整攻角或使用高升力裝置。因此,我們可以利用類似的引擎動力水平以及與地面的更高距離,來降低噪音水平(在我們模型中,噪音水平是引擎動力和距離的主要函數)。同樣地,隨著橫軸數值增加,顏色會由黃色變成深藍色,表示隨著目標高度增加,燃料消耗亦會增加。然而,透過更仔細的分析,我們可以看出飛機在處於最高高度時會消耗最多的燃料,而在最低高度卻不表示燃耗最低。其中的轉折點位於大約 19,000 英尺的高度,與燃耗最低點接近。帕累托前沿位於這個轉折點附近,令優化結果得到驗證。我們發現由於設計空間受到用作產生離散設計變量而訂明的區間所限制,因此帕累托前沿集的基數可能很小。

2.香港至台北
圖 10 頂部顯示了從香港國際機場到 ENVAR 的高度航道,而底部則顯示了包括設計變量的相應燃料消耗及累積感知到的噪音水平。這裡的累積感知到的噪音水平亦僅與爬升航段對應。飛機的起飛重量設定為 2XX,XXX 公斤(因保密原因而屏蔽),這是基於 QAR 數據的平均值。頂部的航道圖顯示了在起飛結束時Dubins航道的飛行距離,以及加速爬升結束時 PA*S 的飛行距離,並且符合恆定的馬赫數巡航段。
圖中顯示由模擬生成的可行起飛高度航道,與 QAR 航道幾乎相同,同時起飛期間 QAR 航道的變化很小。主要差異出現在起飛接近結束時,其中在後續的爬升階段前,大部分 QAR 航道在短時間內均保持水平飛行,這在我們的高度航道構思中並未加以考慮。雖然模型存在這種差異,但是對於在優化中所產生的可行解決方案,大部分 QAR 航道仍處於當中的操作範圍內(淺藍色區域)。我們觀察到在這個短暫的水平飛行階段後,各個 QAR 航道的爬升角會急劇增加。在這個階段,航道會依循與高爬升率解決方案相似的模式,同時亦與帕累托前沿集的航道相似。這種模式在爬升階段結束時會偏離至兩個高度:在約 37,000 英尺及約 35,000 英尺的高度巡航。這些高度亦在解決方案的操作範圍內,而帕累托前沿集則分佈在 35,000 英尺的巡航高度附近。
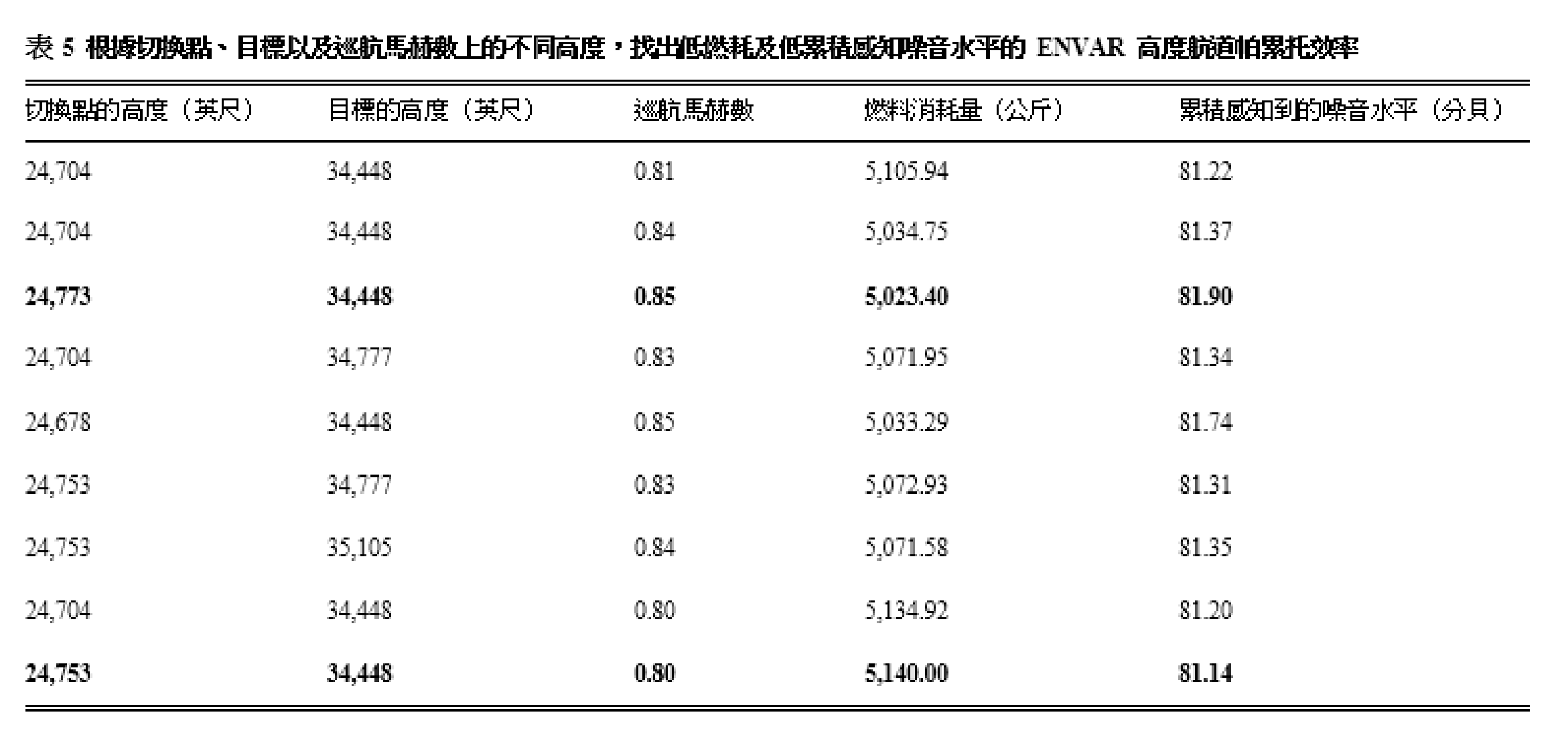
圖 10 底部顯示了三個離散設計變量(巡航馬赫數、切換點高度及目標高度)的分佈,以及其對目標函數的影響(燃料消耗及累積感知到的噪音水平)。左邊首三列的橫軸顯示了設計變量領域,而最後兩列則顯示了目標函數範圍。最頂兩行的縱軸代表了巡航馬赫數和目標高度,而最後兩行則代表目標。每列頂部的圖表是柱狀圖,沿著對角線的三個柱狀圖顯示了設計空間產生的樣本分佈,最後兩個柱狀圖則是這些樣本的輸出。在優化期間,除了接近上限目標高度的設計變量外,其餘大部分都分佈均勻。我們從第一列觀察到目標位置的離散巡航馬赫數和離散高度是以恆定區間產生,同時亦觀察到隨著切換點高度增加,燃料消耗和累積感知到的噪音水平便會降低。帕累托前沿集中在第一列圖形的右邊,表示最佳集合位於與較高爬升角對應的切換點高度上限附近,這亦可在圖 10(頂部)的航道圖中觀察得到。帕累托前沿集中在第三列圖形的左邊,表示最佳集合位於目標高度的下限附近。我們從第四列中觀察到隨著燃料消耗增加,噪音水平亦會有增加傾向。表 5 列出了帕累托前沿,並以粗體字表示將燃料消耗和噪音減到最低的解決方案。我們觀察到雖然兩者之間的噪音水平差異甚微,但在馬赫數較低(0.8)下,燃料消耗會較高,差異明顯,這是因為 777-300ER 的巡航速度約為 0.84 (這是本研究所採用飛機的參照值)。表 6 列出了優化中的燃料消耗範圍和累積感知噪音水平,以清晰地顯示出我們制定的優化問題構思所得出的效果。表 6 中的「解決方案」列是指在優化過程中估算的所有解決方案,而帕累托前沿列則是指當中所選出的最佳集合。即使 BEKOL 解決方案的噪音範圍和 ENVAR 解決方案的燃料範圍很大,但帕累托前沿的燃料和噪音範圍仍遠低於那些解決方案。換言之,任何帕累托前沿選項,均能在未有決定優先選擇的情況下得出最佳解決方案,同時無需在將燃耗和感知噪音水平減到最低之間的權衡明顯的利弊。

IV. 結論
本文提出了一個優化飛行航道的方法,以在飛機離場期間沿著飛行航道降低燃料消耗及累積感知到的噪音水平。當中所採用的方法考慮了航班目的地、跑道角度、機場附近的飛機間隔、障礙物、人口密集地區以及轉向情況,從而為從機場飛往強制性 ATS 位置報告點的飛機產生一組四維的離場航道,以進行 SID 規劃,以及協助飛行規劃人員和機師作出決策。我們所制定的策略會依次執行地平面航道規劃和高度航道規劃,其中前者會產生出包含初步及後續離場航道的最短航道。我們亦利用Dubins航道法來確定初步離場航道是否符合跑道角度和飛機間隔方向的限制。另外,我們亦制定了包含轉向限制的考量人口因素 A* 演算法,以規劃後續離場航道,從而符合與障礙物、人口密集區域及轉向運動相關的限制。高度航道是透過解構飛行運動縱向控制公式而得出。我們使用 ANP 數據庫以及透過評估飛行動力學而得出的性能參數,計算出航道沿途的累積感知到的噪音水平和燃料消耗量。至於高度航道的燃耗及噪音水平點的非支配集,則是利用經改良的 NSGA-II 進行離散優化,透過多目標優化得到結果。我們在從香港國際機場出發的兩個飛行情境中採用了制定的方法,以針對與波音 777-300ER 相似並配備 GE90-115B 引擎的飛機來研究航道規劃。包含轉向限制的考量人口因素 A* 方法,透過圖像比較而得出與標準儀表離場程序(SID)航道及某些實際快速存取記錄器(QAR)航道非常相似的航道。多目標優化的結果顯示燃料及噪音水平降低的趨勢,會受到較高飛行層的切換點高度、馬赫數以及強制性 ATS 位置報告點的高度所影響。此外,我們透過優化得出一小組最佳解決方案,其中的燃耗最大可減少 120 公斤,感知到的噪音變化最大可減少 0.8 分貝。這個方法可進一步用於分析飛行航道,並延伸至無人機和城市空中移動交通的航道規劃,尤其是涉及與航空運輸相關的複雜限制和多個決策標準。雖然我們對香港國際機場離港航班施加了符合現實的限制,但是在這項研究中,我們並未考慮空中交通的互動情況和天氣條件。假如將這項研究擴展以包括這些因素,我們便能在香港國際機場四周更全面地協調和優化離場航線。透過加入相關限制,這個方法亦可以廣泛地採用,從而適用於其他機場。
鳴謝
本研究工作獲得香港科技大學創業補助金(項目編號: R9354)的資助,以及在研究上得到周凱旋基金會協助。作者們在此感謝國泰航空有限公司根據其與香港科技大學機械及航空航天工程系之間的數據合作協議,為本研究提供所需要的數據。此外,對於為本研究提供了實用建議的首爾地區航空辦公室 Young-jong Lee 以及香港民航處 Raymond Li、為本文進行仔細核對工作的 Arjit Seth、以及為本文提供具建設性意見和實用建議的諸位匿名審閱人員,作者們亦希望表示衷心謝意。
參考資料:
- Mahashabde, A., Wolfe, P., Ashok, A., Dorbian, C., He, Q., Fan, A., Lukachko, S., Mozdzanowska, A., Wollersheim, C., Barrett, S. R., et al., "Assessing the Environmental Impacts of Aircraft Noise and Emissions," Progress in Aerospace Sciences, Vol. 47, No. 1, 2011, pp. 15–52. https://doi.org/10.1016/j.paerosci.2010.04.003
- Ho-Huu, V., Hartjes, S., Visser, H., and Curran, R., "Integrated Design and Allocation of Optimal Aircraft Departure Routes," Transportation Research Part D: Transport and Environment, Vol. 63, Aug. 2018, pp. 689–705. https://doi.org/10.1016/j.trd.2018.07.006
- Bertsch, L., and Isermann, U., "Noise Prediction Toolbox Used by the DLR Aircraft Noise Working Group," INTER-NOISE the 42nd International Congress and Exposition on Noise Control Engineering, Vol. 247, Inst. of Noise Control Engineering, Reston, VA, 2013, pp. 805–813, https://www.researchgate.net/profile/Lothar-Bertsch/publication/257773363_Noise_prediction_toolbox_used_by_the_DLR_aircraft_noise_working_group/links/00b49525d6a02d5634000000/Noise-prediction-toolbox-used-by-the-DLR-aircraft-noise-working-group.pdf
- Casalino, D., Diozzi, F., Sannino, R., and Paonessa, A., "Aircraft Noise Reduction Technologies: A Bibliographic Review," Aerospace Science and Technology, Vol. 12, No. 1, 2008, pp. 1–17. https://doi.org/10.1016/j.ast.2007.10.004
- Ho-Huu, V., Hartjes, S., Pérez-Castán, J., Visser, H., and Curran, R., "A Multilevel Optimization Approach to Route Design and Flight Allocation Taking Aircraft Sequence and Separation Constraints into Account," Transportation Research Part C: Emerging Technologies, Vol. 117, Aug. 2020, Paper 102684. https://doi.org/10.1016/j.trc.2020.102684
- Kim, D., Lyu, Y., and Liem, R. P., "Flight Profile Optimization for Noise Abatement and Fuel Efficiency During Departure and Arrival of an Aircraft," AIAA Aviation 2019 Forum, AIAA Paper 2019-3622, 2019. https://doi.org/10.2514/6.2019-3622
- Patrón, R. S. F., Botez, R. M., and Labour, D., "Vertical Profile Optimization for the Flight Management System CMA-9000 Using the Golden Section Search Method," IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Inst. of Electrical and Electronics Engineers, New York, 2012, pp. 5482–5488. https://doi.org/10.1109/IECON.2012.6389517
- "Procedure for Air Navigation Services (PANS)—Aircraft Operations," Procedure, International Civil Aviation Organization, Montreal, 2018, https://store.icao.int/en/procedures-for-air-navigation-services-pans-aircraft-operations-volume-i-flight-procedures-doc-8168
- Zachary, D. S., Gervais, J., and Leopold, U., "Multi-Impact Optimization to Reduce Aviation Noise and Emissions," Transportation Research Part D: Transport and Environment, Vol. 15, No. 2, 2010, pp. 82–93. https://doi.org/10.1016/j.trd.2009.09.005
- Prats, X., Puig, V., Quevedo, J., and Nejjari, F., "Multi-Objective Optimisation for Aircraft Departure Trajectories Minimising Noise Annoyance," Transportation Research Part C: Emerging Technologies, Vol. 18, No. 6, 2010, pp. 975–989. https://doi.org/10.1016/j.trc.2010.03.001
- Torres, R., Chaptal, J., Bès, C., and Hiriart-Urruty, J.-B., "Optimal, Environmentally Friendly Departure Procedures for Civil Aircraft," Journal of Aircraft, Vol. 48, No. 1, 2011, pp. 11–22. https://doi.org/10.2514/1.C031012
- Ho-Huu, V., Hartjes, S., Visser, H. G., and Curran, R., "An Efficient Application of the MOEA/D Algorithm for Designing Noise Abatement Departure Trajectories," Aerospace, Vol. 4, No. 4, Nov. 2017, pp. 1–15. https://doi.org/10.3390/aerospace4040054
- Filippone, A., Zhang, M., and Bojdo, N., "Validation of an Integrated Simulation Model for Aircraft Noise and Engine Emissions," Aerospace Science and Technology, Vol. 89, June 2019, pp. 370–381. https://doi.org/10.1016/j.ast.2019.04.008
- Thomas, J., and Hansman, R. J., "Evaluation of the Impact of Transport Jet Aircraft Approach and Departure Speed on Community Noise," Massachusetts Inst. of Technology, Cambridge, MA, 2020, https://rosap.ntl.bts.gov/view/dot/56957
- Chai, R., Savvaris, A., Tsourdos, A., Xia, Y., and Chai, S., "Solving Multiobjective Constrained Trajectory Optimization Problem by an Extended Evolutionary Algorithm," IEEE Transactions on Cybernetics, Vol. 50, No. 4, 2018, pp. 1630–1643. https://doi.org/10.1109/TCYB.2018.2881190
- Kant, K., and Zucker, S. W., "Toward Efficient Trajectory Planning: The Path-Velocity Decomposition," International Journal of Robotics Research, Vol. 5, No. 3, 1986, pp. 72–89. https://doi.org/10.1177/027836498600500304
- Hartjes, S., and Visser, H., "Efficient Trajectory Parameterization for Environmental Optimization of Departure Flight Paths Using a Genetic Algorithm," Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Vol. 231, No. 6, 2017, pp. 1115–1123. https://doi.org/10.1177/0954410016648980
- Zhang, Y., Zhang, R., and Li, H., "Graph-Based Path Decision Modeling for Hypersonic Vehicles with No-Fly Zone Constraints," Aerospace Science and Technology, Vol. 116, Sept. 2021, Paper 106857. https://doi.org/10.1016/j.ast.2021.106857
- Zhang, Z., Du, R., and Cowlagi, R. V., "Randomized Sampling-Based Trajectory Optimization for UAVs to Satisfy Linear Temporal Logic Specifications," Aerospace Science and Technology, Vol. 96, Jan. 2020, Paper 105591. https://doi.org/10.1016/j.ast.2019.105591
- Qian, K., Liu, Y., Tian, L., and Bao, J., "Robot Path Planning Optimization Method Based on Heuristic Multi-Directional Rapidly-Exploring Tree," Computers & Electrical Engineering, Vol. 85, July 2020, Paper 106688. https://doi.org/10.1016/j.compeleceng.2020.106688
- Li, Z., Yang, X., Sun, X., Liu, G., and Hu, C., "Improved Artificial Potential Field Based Lateral Entry Guidance for Waypoints Passage and No-Fly Zones Avoidance," Aerospace Science and Technology, Vol. 86, March 2019, pp. 119–131. https://doi.org/10.1016/j.ast.2019.01.015
- Wang, H., and Pan, W., "Research on UAV Path Planning Algorithms," IOP Conference Series: Earth and Environmental Science, Vol. 693, IOP Publ., Bristol, England, U.K., 2021, Paper 012120, https://iopscience.iop.org/article/10.1088/1755-1315/693/1/012120/pdf
- Haghighi, H., Asadi, D., and Delahaye, D., "Multi-Objective Cooperated Path Planning of Multiple UAVs Based on Revisit Time," Journal of Aerospace Information Systems, Vol. 18, No. 12, 2021, pp. 1–14. https://doi.org/10.2514/1.I010866
- Heidari, H., and Saska, M., "Collision-Free Trajectory Planning of Multi-Rotor UAVs in a Wind Condition Based on Modified Potential Field," Mechanism and Machine Theory, Vol. 156, Feb. 2021, Paper 104140. https://doi.org/10.1016/j.mechmachtheory.2020.104140
- Guo, J., Li, B., and Ji, Y., "A Control Parametrization Based Path Planning Method for the Quad-Rotor UAVs," Journal of Industrial & Management Optimization, Vol. 13, No. 5, March 2021, pp. 1079–1100. https://doi.org/10.3934/jimo.2021009
- Huang, Y., Chen, J., Wang, H., and Su, G., "A Method of 3D Path Planning for Solar-Powered UAV with Fixed Target and Solar Tracking," Aerospace Science and Technology, Vol. 92, Sept. 2019, pp. 831–838. https://doi.org/10.1016/j.ast.2019.06.027
- Abd Algfoor, Z., Sunar, M. S., and Kolivand, H., "A Comprehensive Study on Pathfinding Techniques for Robotics and Video Games," International Journal of Computer Games Technology, Vol. 2015, April 2015, Paper 736138. https://doi.org/10.1155/2015/736138
- Kavraki, L., and Latombe, J. C., "Randomized Preprocessing of Configuration Space for Path Planning: Articulated Robots," Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’94), Vol. 3, Inst. of Electrical and Electronics Engineers, New York, 1994, pp. 1764–1771. https://doi.org/10.1109/IROS.1994.407619
- Karaman, S., and Frazzoli, E., "Sampling-Based Algorithms for Opti-mal Motion Planning," International Journal of Robotics Research, Vol. 30, No. 7, 2011, pp. 846–894. https://doi.org/10.1177/0278364911406761
- Andrews, J. R., "Impedance Control as a Framework for Implementing Obstacle Avoidance in a Manipulator," Master's Thesis, Dept. of Mechanical Engineering, Massachusetts Inst. of Technology, Cambridge, MA, 1983.
- Koren, Y., and Borenstein, J., "Potential Field Methods and Their Inherent Limitations for Mobile Robot Navigation," Proceedings of 1991 IEEE International Conference on Robotics and Automation, Vol. 2, April 1991, pp. 1398–1404. https://doi.org/10.1109/ROBOT.1991.131810
- Betts, J. T., "Survey of Numerical Methods for Trajectory Optimization," Journal of Guidance, Control, and Dynamics, Vol. 21, No. 2, 1998, pp. 193–207. https://doi.org/10.2514/2.4231
- Petereit, J., Emter, T., Frey, C. W., Kopfstedt, T., and Beutel, A., "Application of Hybrid A* to an Autonomous Mobile Robot for Path Planning in Unstructured Outdoor Environments," ROBOTIK 2012; 7th German Conference on Robotics, Verband Deutscher Elektrotech-niker (VDE), May 2012, pp. 1–6, https://ieeexplore.ieee.org/document/6309512
- The Defence Mapping Agency (DMA) World Geodetic System 84 Development Committee, "Department of Defense World Geodetic System 1984: Its Definition and Relationships with Local Geodetic Systems," United States Defense Mapping Agency TR 8350.2, Sept. 1991, https://ia800106.us.archive.org/29/items/DTIC_ADA280358/DTIC_ADA280358.pdf
- "Aeronautical Information Manual," Federal Aviation Administration, 2008, https://www.faa.gov/air_traffic/publications/atpubs/aim_html/chap1_section_2.html
- McGrath, C. N., and Macdonald, M., "General Perturbation Method for Satellite Constellation Reconfiguration Using Low-Thrust Maneuvers," Journal of Guidance, Control, and Dynamics, Vol. 42, No. 8, 2019, pp. 1676–1692. https://doi.org/10.2514/1.G003739
- Dubins, L. E., "On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents," American Journal of Mathematics, Vol. 79, No. 3, 1957, pp. 497–516, https://www.jstor.org/stable/2372560
- Jha, B., Chen, Z., and Shima, T., "On Shortest Dubins Path via a Circular Boundary," Automatica, Vol. 121, Nov. 2020, Paper 109192. https://doi.org/10.1016/j.automatica.2020.109192
- Hart, P. E., Nilsson, N. J., and Raphael, B., "A Formal Basis for the Heuristic Determination of Minimum Cost Paths," IEEE Trans- actions on Systems Science and Cybernetics, Vol. 4, No. 2, 1968, pp. 100–107. https://doi.org/10.1109/TSSC.1968.300136
- Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T., "A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II," IEEE Transactions on Evolutionary Computation, Vol. 6, No. 2, 2002, pp. 182–197. https://doi.org/10.1109/4235.996017
- Mailund, T., "Divide and Conquer and Dynamic Programming," Introduction to Computational Thinking, Springer, New York, 2021, pp. 247–288. https://doi.org/10.1007/978-1-4842-7077-6_9
- Kim, D., Seth, A., and Liem, R. P., "Data-Enhanced Dynamic Flight Simulations for Flight Performance Analysis," Aerospace Science and Technology, Vol. 121, Feb. 2022, Paper 107357. https://doi.org/10.1016/j.ast.2022.107357
- "Standard Atmosphere," ISO/TC 20/SC 6, International Organization for Standardization, Geneva, 1975, https://www.iso.org/standard/7472.html
- Polhamus, E. C., A Simple Method of Estimating the Subsonic Lift and Damping in Roll of Sweptback Wings, Vol. 1862, NACA, 1949, https://ntrs.nasa.gov/citations/19930082534
- Dubs, F., "ProfIlform und Polare," Aerodynamik der reinen Unterschallströmung, Vol. 1, Springer, Berlin, 2013, pp. 167–235. https://doi.org/10.1007/978-3-0348-5295-1
- Jahanmiri, M., "Aircraft Drag Reduction: An Overview," Chalmers Univ. of Technology, Gothenburg, Sweden, 2011, https://publications.lib.chalmers.se/records/fulltext/137214.pdf
- Bouhlel, M. A., Hwang, J. T., Bartoli, N., Lafage, R., Morlier, J., and Martins, J. R. R. A., "A Python Surrogate Modeling Framework with Derivatives," Advances in Engineering Software, Vol. 135, Sept. 2019, Paper 102662. https://doi.org/10.1016/j.advengsoft.2019.03.005
- The Society of Automotive Engineers (SAE) A-21 Aircraft Noise Measure and Noise Aviation Emission Modeling Committee, "Procedure for the Calculation of Airplane Noise in the Vicinity of Airports," Society of Automotive Engineers, Aerospace Information Rept. 1845, Sept. 1995. https://doi.org/10.4271/AIR1845
- European Civil Aviation Conference (ECAC), "Report on Standard Method of Computing Noise Contours Around Civil Airports," Euro-pean Civil Aviation Conference, ECAC.CEAC Doc 29, 2016, https://www.ecac-ceac.org/images/documents/ECAC-Doc_29_4th_edition_Dec_2016_Volume_1.pdf
- Boeker, E. R., Dinges, E., He, B., Fleming, G., Roof, C. J., Gerbi, P. J., Rapoza, A. S., Hermann, J., et al., "Integrated Noise Model (INM) Version 7.0 Technical Manual," United States Federal Aviation Administration Office of Environment and Energy, 2008, https://www.faa.gov/about/office_org/headquarters_offices/apl/research/models/inm_model/inm7_0c/media/INM_7.0_Technical_Manual.pdf
註:
‡ https://www.ais.gov.hk
¶ https://www.ais.gov.hk
§ https://earth.google.com
** www.cad.gov.hk/english/ac_path.html
†† https://sedac.ciesin.columbia.edu/data/set/gpw-v4-admin-unit-center-points-population-estimates-rev11/data-download
‡‡ https://www.aircraftnoisemodel.org/
作者:
香港科技大學機械及航空航天工程系助理教授Rhea Liem教授
香港科技大學博士後研究員Dajung Kim博士
副主編:
I Hwang
2023年3月

