过去数十年,随著空中交通愈趋繁忙,降低飞机噪音是持份者需要面对的其中一项重大挑战。但是要在飞行途中降低噪音,便可能会消耗更多飞机燃料,对于航空公司成本管理而言,这是一个必须考虑的因素。我们将会在本文提出一种规划飞行航道的方法,当中的目标是降低人们感知到的噪音以及燃料消耗。我们将飞机的航迹分拆成地平面和高度两条航道,以模拟航空运输所面对的相关限制,并且会利用Dubins航道法及经改良的A*演算法,来找出地平面投影的最短航道,当中的演算法会根据飞行目的地、跑道角度、机场附近的飞机间隔、人口分布,以及飞机转向运动来考虑引导点。另外,我们亦会利用地平面航道计算出的距离,解构飞行运动的纵向公式来确定如何优化高度航道,从而降低人们感知到的噪音以及飞机燃料消耗。为了进行离散优化,我们设计了一个经改良的非支配型排序遗传演算法II (NSGA-II),从而在减少运算难度之下得到最佳高度航道的帕累托前沿(Pareto fronts)。透过模拟从香港国际机场起飞,飞到两个强制位置报告点来展示这个方法的成效。之后,我们会将结果与快速存取记录器 (Quick Access Recorder) 的数据以及标准仪表离场(SID)程序的路径进行比较。虽然这个方法并未考虑在航空运输期间某些会令离场航道规划受到影响的因素,例如天气情况以及空中交通组合,但是得出的地平面航道却与SID的路径十分相似。由此得出高度航道的帕累托前沿,显示可降低燃料消耗以及人们感知到的噪音水平。另外,我们亦根据不同航线的相关飞行物理学,分析了如何在燃料消耗和人们感知到的噪音水平之间权衡利弊。
I. 简介
空中交通的迅速发展,及由此产生的飞机噪音的增加,导致居住在机场附近的居民饱受困扰,影响他们的睡眠,及出现与压力有关的健康问题 [1]。这个问题可以透过飞机设计或空中交通管理等方法来解决 [2]。在飞机设计方面,我们可以设计新的飞机机体及引擎,以降低飞机发出的噪音 [3]。但自1980年代以来,要在不影响营运成本之下透过改变飞机设计来进一步降低噪音,是一件相当困难的事 [4]。至于空中交通管理方面,我们可以改变飞行航道以减少感知到的噪音,例如增加飞机起飞后的爬升率。虽然这个做法较为「务实」,但未能解决将飞机噪音降低的问题,同时可能会令燃料消耗增加 [5]。人们感知到的噪音以及燃料消耗,会受到引擎动力的设定以及飞机与观察者之间距离的变化所影响,情况相当复杂 [6]。燃料消耗会直接影响航空公司的收入,同时亦与空气污染及温室气体排放量成正比 [7]。因此,在优化航机的操作条件时,我们亦必须同时考虑人们感知到的噪音。
在实际情况下,机场四周的离场航道是以标准仪表离场(SID)程序作为指引。SID是指从离场航线开始的起点,直到航途阶段中首个定位点/设施/航点的经编码航行程序,不同的机场会有不同的SID [8]。各国民航当局均按照ICAO Doc. 8168 [8] 中订明的设计标准来设计及公布SID,当中考虑的因素包括但不限于跑道角度、地形、需避开的障碍物、飞机性能、空域管理以及环境问题。根据香港民航处(CAD),在设计SID=时,有关人员会先与持份者(包括营运商/机师及空中交通管制员)进行初步讨论。之后,便会在模拟飞行中测试初步路径在不同天气和承载量下的可飞程度,再在发布该路径前透过实际的航行测试来加以验证。Zachary等人[9]、Prats等人[10]、Torres等人[11]、Ho-Huu等人[12]、Filippone等人[13],以及Thomas和Hansman [14] 进行了优化计算的研究,以在定量标准下改良离场航道的设计程序。这些研究建议采用多目标或多层次的起飞航道规划方法,当中同时考虑到燃料消耗和感知到的噪音水平。然而,据我们所知,这些研究并未根据航行目的地(即本研究考虑的强制性[ATS]位置报告点)、由航行资料汇编(AIP)提供的障碍物限制,以及人口和地形的资讯,来考虑引导点所产生的综合影响。其中有部分研究亦未有将其取得的结果,与现有的SID路径或航班数据进行比较。为了弥补这方面的不足,本文在同时考虑上述所有因素下,提出了一个旨在带来低噪音和低燃料消耗的起飞航道规划方法。
优化具有多个变数限制的航道在电脑运算上是相当慢 [15]。在维持一定的计算效率,并同时在考虑多个不同限制下得出一组最理想的帕累托(Pareto)解决方案上,本研究带来了三个贡献。第一个贡献是将四维航迹规划(三维空间再加上时间)分拆成两个子问题:1) 在主要考虑与地理/地形相关的限制(例如禁飞区、人口密集的非航行及升降区,以及航道角度限制)下,规划投射在地球表面的最短航道;及 2) 在考虑与垂直飞行性能相关的限制下,沿著最短航道来规划在不同速度下的高度航道,以降低累积的感知到的噪音水平和燃料消耗。采用分拆方法来规划航迹,是最先是由 Kant 和 Zucker [16] 提出,以因应在包含静态及移动障碍物的动态环境中所进行航迹规划,简化当中所面对的问题。他们的研究提出了一个序列规划的方案,当中第一个步骤是解决航道的纯空间优化问题,第二步则因应第一步所产生的航道,解决时间依存的速度问题。在此强调,首个空间解决方案不会被随后的时间解决方案所影响。然而,由 Hartjes 和 Visser [17] 所提出的航迹分拆方法,均考虑了在两个子问题中(即横向及垂直航道规划)的速度耦合。从垂直航道规划中得出的飞机空速,限制了横向航道规划中的转弯半径。在他们的研究中,各航道是在订明了从出发地到目的地之间固定数量的航段后确定出来的。横向航道规划中的航段类型,仅限于直线及恒定半径的转弯航段;而垂直航道规划则受到航空站位置的固定高度及空速所限制。本文提出的航迹分拆方法,并不会对航道航段的类型或数量产生限制;而航空站的高度则是其中一个受 AIP 限度所限制的设计变量。借着这些构思,我们便能广泛地研究设计空间,并且透过分拆方法来简化多目标的优化工作。我们将本研究中的四维航迹规划,分拆成地平面航道及高度航道,并以地平面航道的弧长连结起来。当在地平面航道规划中解决了将这个弧长减到最短的最短航道问题后,便会估算高度航道规划中燃料消耗及累积的感知到的噪音水平。在地平面航道规划中,我们单独地考虑了在不运用速度耦合下可能会被忽略的转弯半径限制。
本研究的第二个贡献,就是为最短航道规划提出一个崭新的方法,让我们能考虑非可取区域、禁飞区以及航道角度的限制。在文献中,大部分模拟航道规划都已经能够避开静态障碍物(这些障碍物是一些航迹无法越过的地形和地理限制)的航道 [18-21]。除了静态障碍物外,我们的方法亦引入了非可取程度。非可取程度的估算涉及整个航道规划范围,得出的解决方案往往会将航道改变至非可取程度较低的区域。由于本研究中的非可取程度是根据人口分布来确定,因此我们认为在人群可能受到飞机噪音影响较大的区域附近,非可取程度会较高。我们将这种非可取情况称为势场的排斥力,是其中一种航道规划方法。航道规划方法大致分成四种类型 [22]:1) 以网格为基础的网络 [18、23]、2) 以采样为基础的方法 [19、20]、3) 势场 [21、24],及 4) 最佳控制理论 [25、26]。以网格为基础的网络能在起点和目标之间订明的网格上解决最短航道的问题。虽然透过这个方法将资讯汇聚起来并不复杂,但是视乎网格的形状,这个方法可能不符合物理要求 [27]。至于以采样为基础的方法则是以样本空间,而非透过在预先建立的网格上进行搜寻来找出最佳航道 [28]。虽然这个方法可在短时间内计算出结果,但却可能会在进行大范围规划时产生出效率欠佳的航道 [29]。势场方法能模拟朝著目标移动的物体,当中会将目标模拟成具有吸引力的区域,而障碍物则为具有排斥力的区域 [30]。由于计算时间短,因此这些方法适用于实时航道规划,但答案可能会趋向于局部最小值 [31]。最佳控制方法是根据运动控制公式来优化特定性能指标。其中所产生的航道虽然符合物理要求,但是收敛却未必保证成功 [32]。最近的各种做法已经将这些方法组合起来,以弥补它们各自的缺点 [33]。举例来说,将以网格图形和采样为基础的方法结合,以平整前者因网格规范而产生出不符合物理要求的航线。我们在本研究中结合了这四种方法,以能在快速且符合物理要求的情况下规划地平面航道,从而模拟出各种航空运输限制。首先是将Dubins航道(最佳控制方法)应用到靠近跑道的 SID 程序开始部分。由于跑道角度和飞行航线的飞机间隔要求严格限制了起飞航道,因此引入Dubins航道,以模拟具有开始航向和航空站航向限制的起飞航道规划。第二步是提出一个以人口密度为主要考虑下,在Dubins航道终点到目标之间包含转向限制的考量人口因素A*演算法。这个演算法将势场和以采样为基础的方法,纳入到以网格为基础的方法中。A*演算法是一种以网格寻找最短航道的常用方法,由于它完整、易于修改以及能够快速计算,因此我们的方法亦按此制定出来。正如上文所述,由于我们会将以人口密度为基础的势场方法结合至 A* 演算法中,因此便能在量化的感知到的噪音水平下因应人口来规划最短航道。根据以采样为基础的方法,我们的方法透过搜寻样本空间来平整航道。我们在这个样本空间搜寻中引入了航道角限制,以协助处理与飞机适航性相关的因素。透过将这些方法结合,便能令我们的做法更为实际,并且能配合现实世界的应用情况。
最后一个贡献,就是在整数规划下透过多目标优化来找出高度航道。在规划地平面航道后,我们便会沿著将累积的感知到的噪音和燃料消耗降到最低的地平面航道,来计算高度航道。由于燃料消耗和累积的感知到的噪音水平耦合在一起,因此在没有预先订明取向的情况下,将两者降到最小的解决方案并不能产生出最佳航道 [6]。这些解决方案会以帕累托前沿集 Pareto front set 的方式表达,当中显示了决策过程中权衡利弊的敏感程度。假如设计变量的数目较少以及无法准确知道目标函数剖面,则帕累托前沿集主要会透过进化演算法得出,继而无法保证连续性。透过进化演算法来优化多个目标需要很长的计算时间 [17],并且难以收敛。为了解决这个问题,我们将设计变量限制为具有预先订明均匀区间的整数,其中区间是合理地根据每个变量的物理意义而选取的。这个范围的限制避免了为相对不显著的变化进行函数估算,例如,一米内的高度变化。此外,在这种设定下,由于设计空间的大小可以透过有限数量的设计变量来估计,因此我们可以合理地设定进化演算法中的函数估算次数。
总括而言,我们制定了一个能优化多目标飞行航道的方法,当中考虑了各种实质限制,以模拟离场期间航空运输的操作。另外亦将四维的飞行航道规划分拆成依次的地平面和高度航道规划程序,从而减少计算时间。我们提出了根据飞行目的地、静态障碍物、跑道角度、机场附近的飞机间隔、以人口分布为基础的非可取区域,以及转向限制来考虑引导点的地平面航道规划;同时亦制定了具有整数规划的高度航道规划,以能有效率地进行运算。我们承认目前所制定的方法仍然存在局限性,如在模拟航空运输中影响离场航道规划的天气和空中交通组合。透过我们的方法,我们规划了从香港国际机场飞往两个不同目的地的飞机航道结果显示找出来的路径与 SID 路径非常相似。因此,本文提出的方法仍然能为决策过程提供帮助,以在考虑航空运输所面对的限制下,确定降低燃料消耗和感知到的噪音的离场飞行航道。
本文的结构如下。第 II 节详细说明与飞行航道规划、多目标优化,以及燃料消耗和噪音预测模型有关的方法。第 III 节因应在两个出发地与目的地之间采用我们所制订的方法,阐述当中的结果和讨论,并将结果与实际的航迹数据进行比较和验证。第 IV 节总结本研究的发现结果并提供结论。
II. 研究方法
本节介绍一个能降低感知到的噪音水平和燃料消耗的飞行航道规划方法。飞行航道是指飞机的航迹,根据世界大地测量系统1984 [34],其以地平面坐标和高度表示。在本研究中,我们将飞行航道分拆成地平面航道和高度航道,其中地平面航道是指飞机在地球表面上的平面投影位置;而高度航道则指飞机在以弧长(在地球表面的累积飞行距离)和高度作为坐标之下于表面上的投影位置。地平面航道和高度航道与累积飞行距离(在地平面航道规划中率先减至最短)结合。当在根据航行规则、转向角度、该地区中居民人数的既定限制下产生出最短地平面航道后,便根据在固定距离位置(与表面弧长对应)的高度变化,得出降低感知到的噪音和燃料消耗水平的最佳高度航道。第 II. A 节详细说明地平面航道的规划方法,而第 II. B 节则详细解释高度航道的规划方法。
A. 地平面航道规划
飞机在进入或离开任何国家空域时,必须在由航空情报服务 (AIS) 指定的位置联络航空交通管制(ATC)塔;此位置称为强制位置报告点。本节详细说明从起飞到 ATS 位置报告点的地平面航道规划方法。所制定的地平面航道规划方法会依次以两个阶段执行航道规划:初步离场阶段及后续离场阶段。初步离场阶段在跑道至定位点开始,其中定位点位于在 AIP 中所描述的直飞定位段上 [35]。在机场附近的首个直飞定位段,其指定端点视为飞机的横向飞机间隔,以供 ATC 在类近时间于各跑道离场期间管理空中交通。后续离场阶段是指从这个定位点至强制位置报告点的航行阶段。
第 II.A.1 节介绍用作计算地平面航道模型的方法。第 II.A.2 节详细说明解决 AIP 所定义的高海拔区域,以及禁飞区,限飞区及危险区的方法‡。第 II.A.3节介绍初步离场阶段的地平面航道规划。第 II.A.4 及 II.A.5 节详细解释后续离场阶段的地平面航道规划方法,其中考虑了包含转向限制的人口分布及航道平整问题。
1. 网格的产生
我们将飞机航迹在地球表面上的投影映射到网格上,以模拟整个地平面航道规划。这个网格是根据地理资料产生。首先,我们会将以测地坐标来代表的地理资讯,转换成笛卡儿坐标。透过指定四个在地球表面的经纬度点,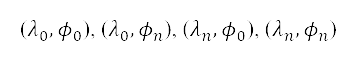 来定义航道规划区域的边界,使封闭的地区能涵盖离场机场及目标的强制位置报告点。之后,我们将测地坐标转换成笛卡儿坐标
来定义航道规划区域的边界,使封闭的地区能涵盖离场机场及目标的强制位置报告点。之后,我们将测地坐标转换成笛卡儿坐标
 。 将
。 将 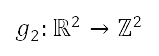 定为从测地坐标换成笛卡儿坐标的坐标变换,定义如下
定为从测地坐标换成笛卡儿坐标的坐标变换,定义如下
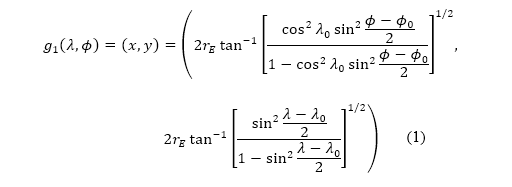
其中 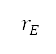 是地球的半径,而
是地球的半径,而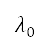 及
及 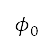 分别表示边界左下角的纬度和经度。坐标变换
分别表示边界左下角的纬度和经度。坐标变换 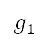 是从目前位置
是从目前位置 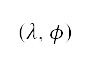 至
至 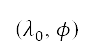 及
及 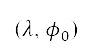 的半正弦距离 [36]
得出。第二步,我们将这个笛卡儿空间离散化,并将映射定义到网格上。笛卡儿领域的轴以均匀区间
的半正弦距离 [36]
得出。第二步,我们将这个笛卡儿空间离散化,并将映射定义到网格上。笛卡儿领域的轴以均匀区间 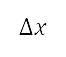 及
及
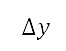 离散开来,以产生网格点。将
离散开来,以产生网格点。将 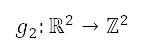 定为从笛卡儿坐标
定为从笛卡儿坐标 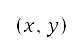 的坐标变换变成网格点
的坐标变换变成网格点 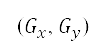 ,定义如下
,定义如下
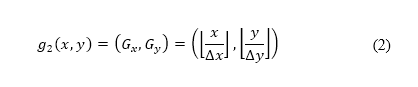
将 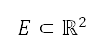 定为代表,地平面航道航迹优化问题的有限领域。将
定为代表,地平面航道航迹优化问题的有限领域。将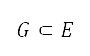 定为
定为 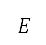 的限制并变成整数,其定义了网格的领域。将以测地坐标表示的空中运输调节限制,透过函数
的限制并变成整数,其定义了网格的领域。将以测地坐标表示的空中运输调节限制,透过函数 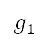 及
及 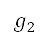 的复合映射到网格上﹐定义如下
的复合映射到网格上﹐定义如下
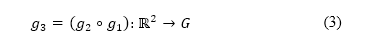
由于 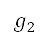 不可逆转,因此随后出现的符号
不可逆转,因此随后出现的符号 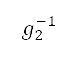 表示它的右逆向,这是包含映射的整数坐标作为
表示它的右逆向,这是包含映射的整数坐标作为  的子集。
的子集。
2. 障碍物的限制
我们在方法中产生的地平面航道,考虑了所有禁飞区情况。禁飞区是飞机不得飞行的区域,例如在 AIP 中指定的禁飞,限飞和危险区域,以及地面高度高于海拔 500 米的区域。图 1
显示了香港空域中的禁飞区及其在网格上的表示方式。我们的方法将禁飞区视为包含障碍物限制的区域。图 1
左边显示了分为四种类型的障碍物:点障碍物,具半径的点、区域边界顶端上的点,以及地图边界。点障碍物是指地面高度高于海拔
500 米的区域,并以红点表示,当中的数据是位置  ,资料撷取自 Google Earth§
,包含点的取样;并透过
,资料撷取自 Google Earth§
,包含点的取样;并透过  .
转换成笛卡儿坐标。具半径的点以及区域边界顶端上的点在图 1
以左边的蓝线表示,与 AIP 中所列出的禁飞,限飞及危险区域对应。这些点亦利用
.
转换成笛卡儿坐标。具半径的点以及区域边界顶端上的点在图 1
以左边的蓝线表示,与 AIP 中所列出的禁飞,限飞及危险区域对应。这些点亦利用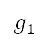 进行转换,然后应用于几何公式中,例如与圆形和线段对应的几何公式,以确定图中以蓝线围著的区域所包括的点。为了限制网格中的飞行航道,我们亦将地图边界模拟成障碍物,以将其视为受限制区域。将
进行转换,然后应用于几何公式中,例如与圆形和线段对应的几何公式,以确定图中以蓝线围著的区域所包括的点。为了限制网格中的飞行航道,我们亦将地图边界模拟成障碍物,以将其视为受限制区域。将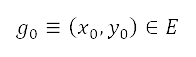 定为障碍物的位置。将
定为障碍物的位置。将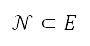 定为
定为 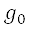 的邻接区,以使
的邻接区,以使 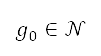 。这个邻接区代表了围绕著障碍物的区域,我们将其定义为障碍物区域。将
。这个邻接区代表了围绕著障碍物的区域,我们将其定义为障碍物区域。将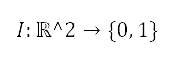 定为代表估算违反限制的指标函数。以下公式定义了障碍物区域的限制违反指标:
定为代表估算违反限制的指标函数。以下公式定义了障碍物区域的限制违反指标:
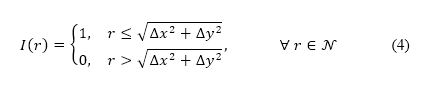
其中从点 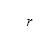 到障碍物
到障碍物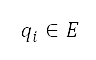 的距离
的距离 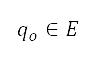 ,是以欧氏范数
,是以欧氏范数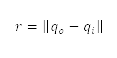 来确定。上述四种障碍物类型的限制违反,均由公式 (4) 来估算,而它们的位置则透过
g映射到网格中。这个过程所产生的障碍物区域,在图 1 的右边以深蓝色表示,而白色区域则代表许可区域。透过防止飞机越过网格上这些限飞区域,来限制地平面航道。
来确定。上述四种障碍物类型的限制违反,均由公式 (4) 来估算,而它们的位置则透过
g映射到网格中。这个过程所产生的障碍物区域,在图 1 的右边以深蓝色表示,而白色区域则代表许可区域。透过防止飞机越过网格上这些限飞区域,来限制地平面航道。
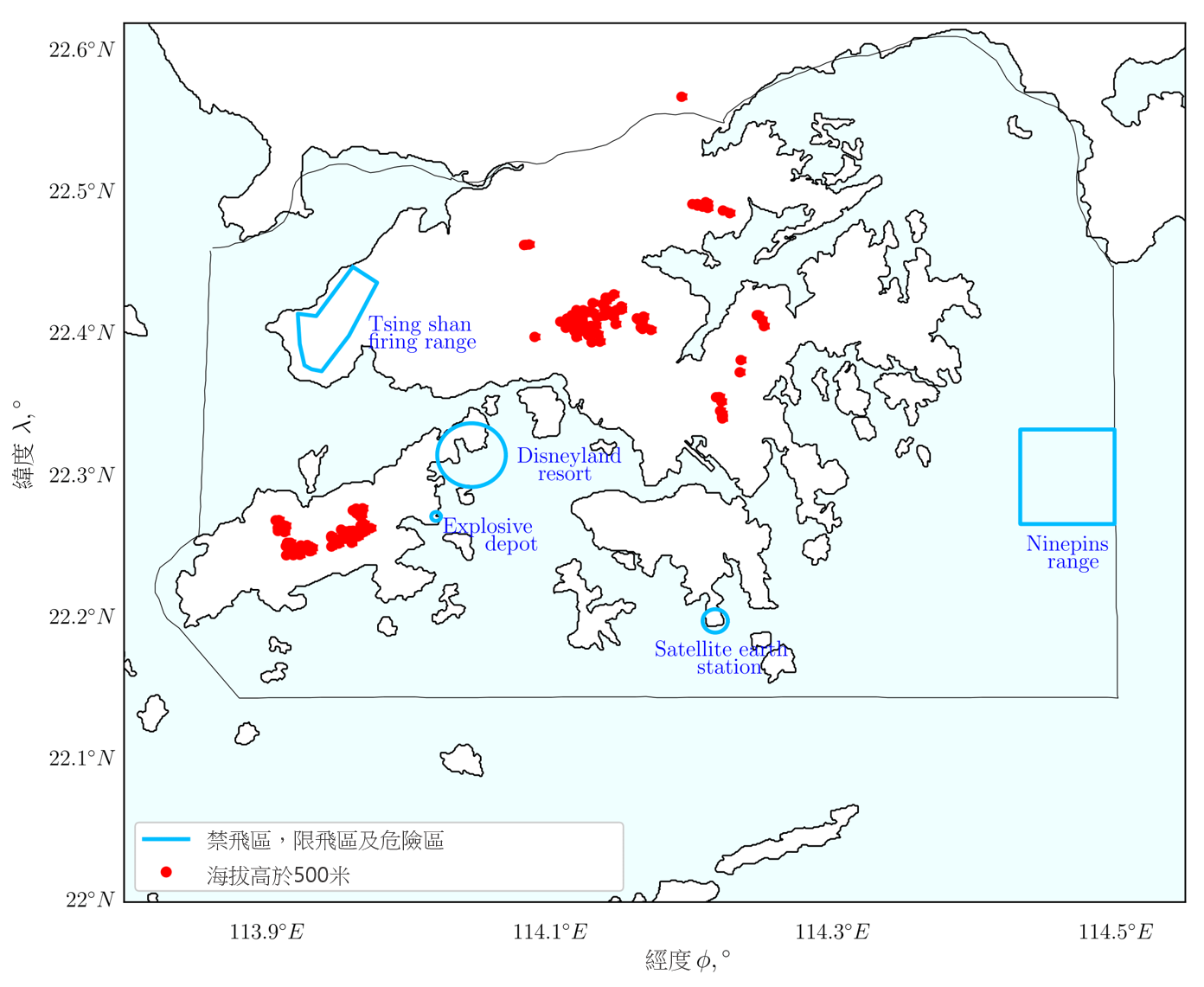
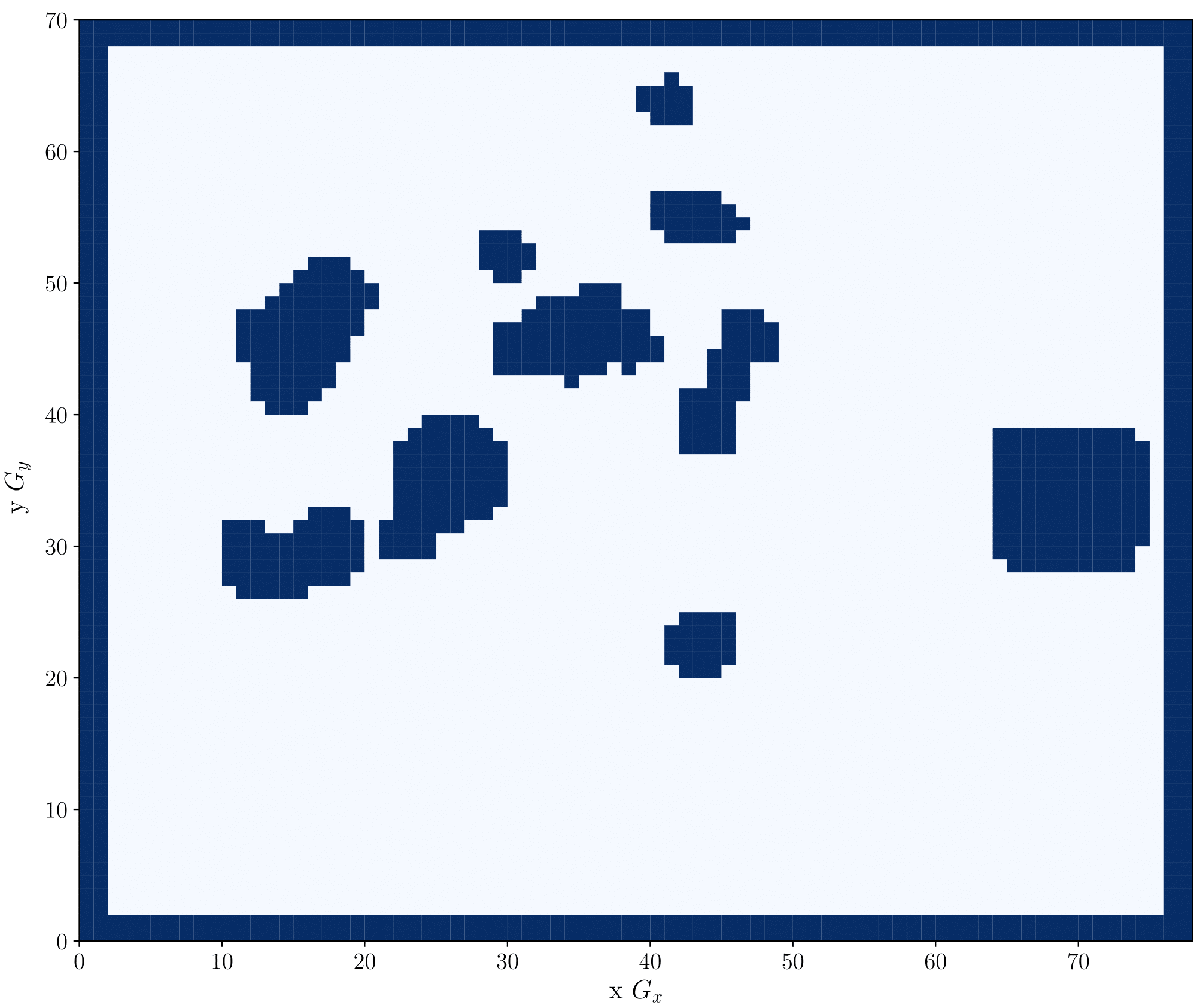
图 1:以大地测量坐标系显示的香港空域禁飞区(左)及使用公式 (4) 以在网格上产生相应的障碍物(右)。
3. 初步离场阶段规划
初步离场阶段的航迹,受到跑道角度以及首个直飞定位段的方向所限制。举例而言,香港国际机场设有两条平行跑道,如图 2 左边所示。在图中,「25L/R」表示左右跑道,其航向角度为 250°;「07L/R」表示左右跑道的航向角为 70°。因应机场附近的飞机间隔,香港民航处指定了六个初步离场航道,从两条跑道的其中一条到三个定位点的其中一点,如图 2 右边所示。**香港 AIP 中的每个 SID 路径,均包括这六条飞行航道的其中一条,因此,我们在本研究中将其视为初步离场航道的限制。
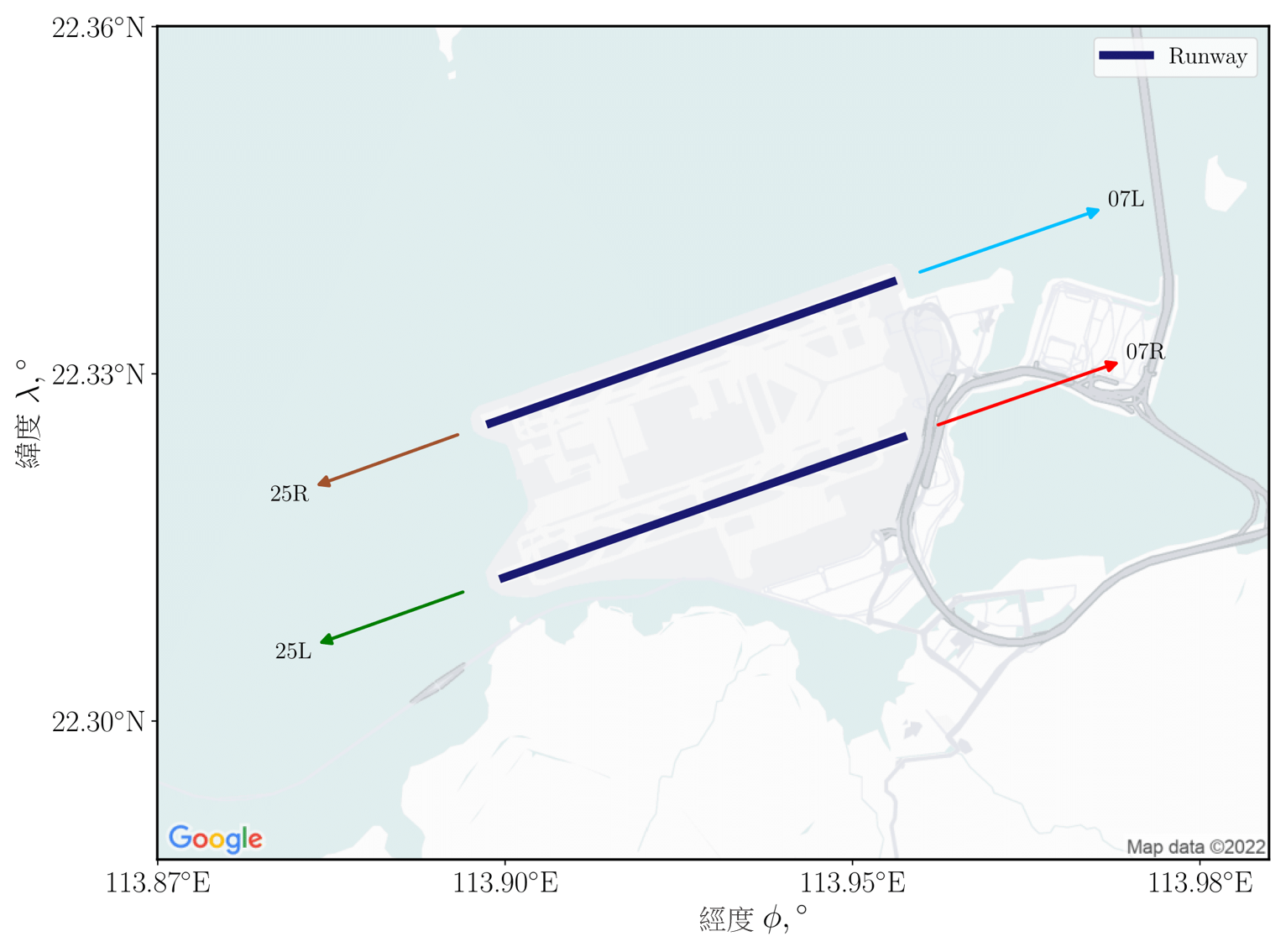
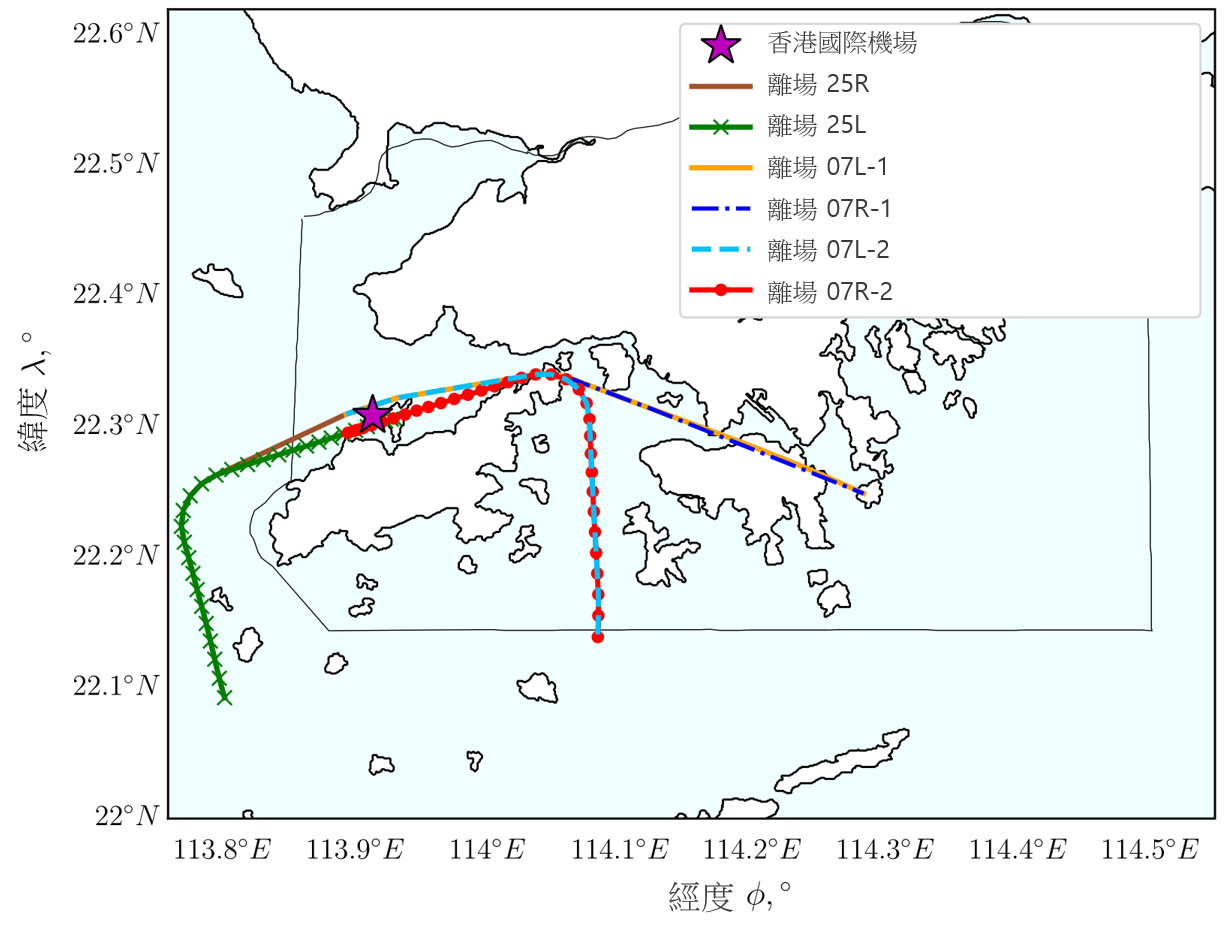
图 2:香港国际机场的跑道配置(左)及从香港国际机场跑道至直飞定位段终点的六条初步离场航道(右)
我们采用Dubins航道方法,以模拟初步离场航道限制。这条航道是空间中连接两点的最短曲线,其中航道的曲率是受到转向/航向角度限制 [37] 。它可在起点和终点的方向上实施切线限制
[38]。这些特点让我们拥有一个方便的框架,以产生与跑道平行并且朝著直飞定位段方向的航道。图 3 显示了Dubins航道的六个配置例子。这些航道是 R-L-S 曲线的复合,其中R 是右转、L 是左转、S
是直线。Dubins航道法首先产生六条航道,当中包含既定的起点  及终点
及终点 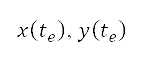 以及相应的航向角度
以及相应的航向角度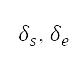 。 这个过程与公式 (5) 中所示的微分公式系统的解答对应,而航道距离 D 则以公式 (6)
透过以下解答来估算
。 这个过程与公式 (5) 中所示的微分公式系统的解答对应,而航道距离 D 则以公式 (6)
透过以下解答来估算
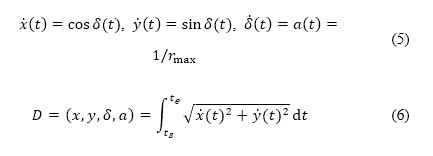
其中的点符号(例如 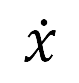 )表示时间导数,
)表示时间导数,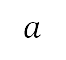 是被最大航向半径限制的航向率
是被最大航向半径限制的航向率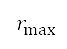 ,
,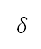 是航向角度,这是单位切线向量
是航向角度,这是单位切线向量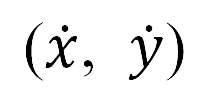 与
与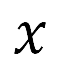 轴之间的角度。 我们选择了具有最短距离的航道。
轴之间的角度。 我们选择了具有最短距离的航道。
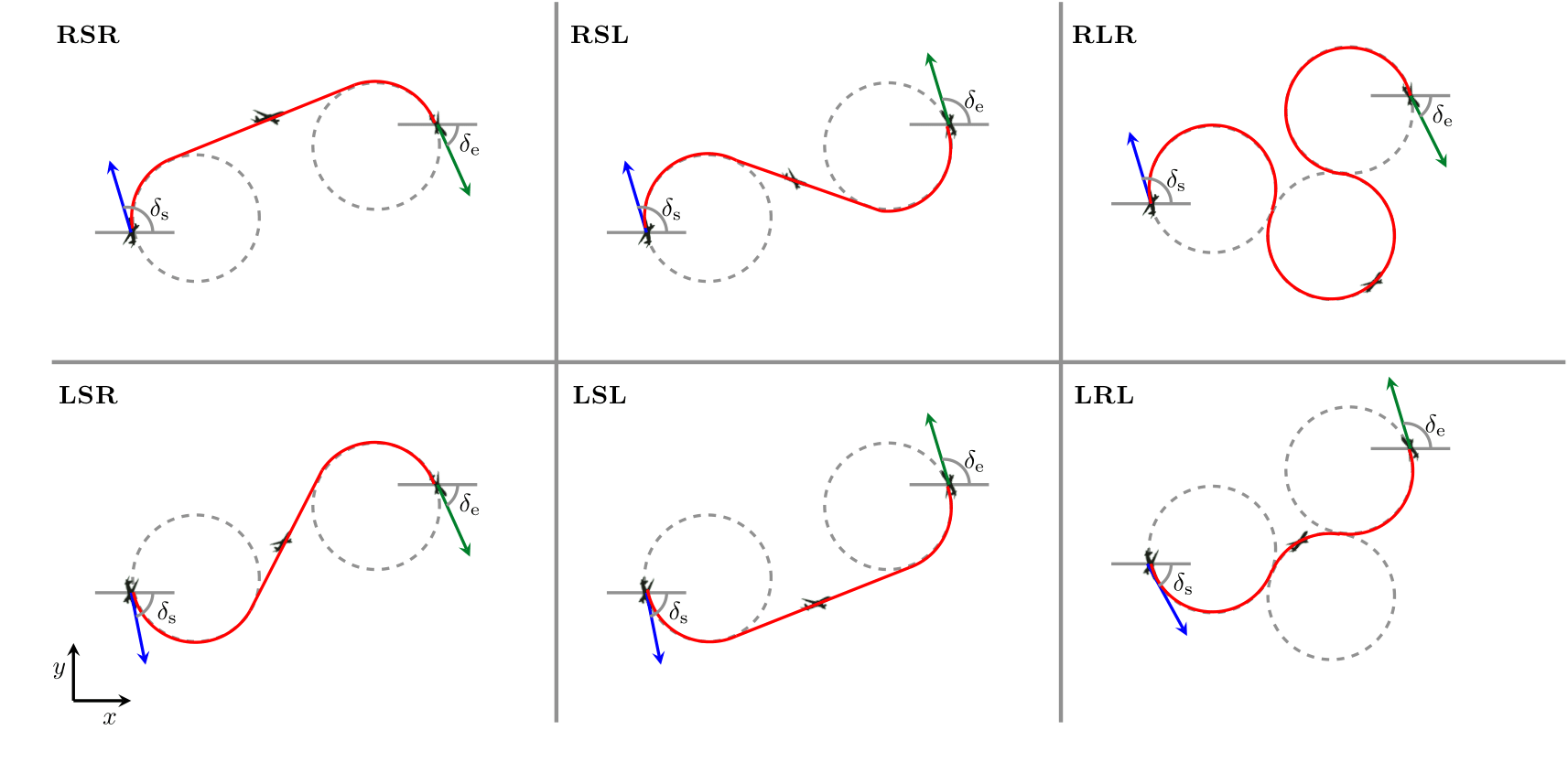
图 3:包括起始和终结航向角度限制(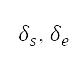 )的六个杜宾斯航道配置,其中 R、L、S
分别代表右转、左转和直线
)的六个杜宾斯航道配置,其中 R、L、S
分别代表右转、左转和直线
4. 包括考量人口因素限制的后续离场阶段规划
对于需要考虑噪音影响的飞行航道规划,我们应优先考虑在人口密集地区降低感知到的噪音。有别于不允许飞行的禁飞区,在这些地区虽然飞机仍然可以飞越人口密集的地区,但并不是可取的选择。为了在航道规划中反映这个特征,我们在
A*演算法中加入了势场公式。A*演算法透过估计当物体从 起点移动至目标时在网格上所航行的距离,来找出于最低成本下在网格上的最短航道 [39]。A*演算法的代价函数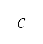 表达如下
表达如下
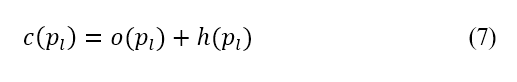
其中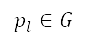 是网格上沿著航道的下一个节点、
是网格上沿著航道的下一个节点、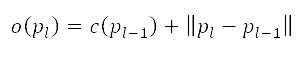 是从起始节点
是从起始节点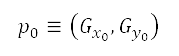 到
到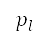 的航道成本,而
的航道成本,而 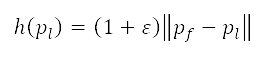 是一个探索成本,表示从
是一个探索成本,表示从 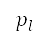 至目标
至目标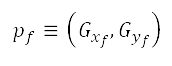 的最便宜成本航道,其中包括最终决定因素
的最便宜成本航道,其中包括最终决定因素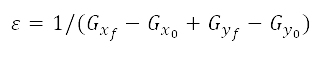 。与标准势场方法不同,在我们的方法中人工势场仅使用排斥力来构成,并没有为目标模拟吸引力。我们称之为考量人口因素
A*
方法。在公式 (7) 中,排斥势是用作代价函数的加权因子。考虑排斥势和最短航程距离的经修正代价函数
。与标准势场方法不同,在我们的方法中人工势场仅使用排斥力来构成,并没有为目标模拟吸引力。我们称之为考量人口因素
A*
方法。在公式 (7) 中,排斥势是用作代价函数的加权因子。考虑排斥势和最短航程距离的经修正代价函数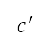 ,是从以下公式得出
,是从以下公式得出
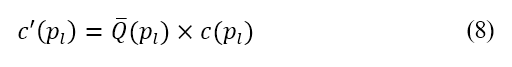
其中 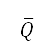 是标准化的排斥势,是根据当地人口数据计算,如下所述。为了取得人口数据,我们采用了行政单位中心位置,以及来自
NASA 社会经济数据及应用中心††的人口估计值。人口数据以中心位置
是标准化的排斥势,是根据当地人口数据计算,如下所述。为了取得人口数据,我们采用了行政单位中心位置,以及来自
NASA 社会经济数据及应用中心††的人口估计值。人口数据以中心位置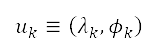 、面积
、面积 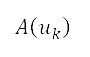 以及次级行政单位的人口估计值
以及次级行政单位的人口估计值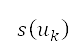 来表示。我们将排斥势的来源放在每一个相应次级行政单位的中心位置,并以圆形表示。透过考虑
来表示。我们将排斥势的来源放在每一个相应次级行政单位的中心位置,并以圆形表示。透过考虑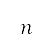 的多个来源,以在网格
的多个来源,以在网格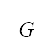 上每一个点的这些
上每一个点的这些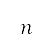 来源所产生的影响总和来找出势场。在测量点
来源所产生的影响总和来找出势场。在测量点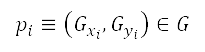 的排斥势
的排斥势 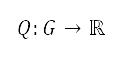 会受到位于
会受到位于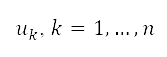 的来源所影响,其中强度
的来源所影响,其中强度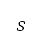 是以位于
是以位于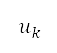 的人口估计值得出,如上所述。位于
的人口估计值得出,如上所述。位于 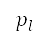 的势(由位于
的势(由位于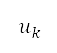 的单一来源触发)亦会受到来源
的单一来源触发)亦会受到来源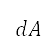 的距离影响,而半径
的距离影响,而半径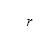 对应于有效区域A,透过下级行政单位的循环表示以
对应于有效区域A,透过下级行政单位的循环表示以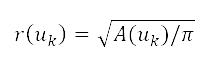 计算。前往来源
计算。前往来源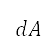 的距离是透过半正矢公式 (Haversine's formula) 计算 [36]。我们发现
的距离是透过半正矢公式 (Haversine's formula) 计算 [36]。我们发现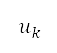 是测地坐标。网格上
是测地坐标。网格上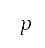 及
及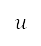 之间的转换,是从
之间的转换,是从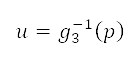 得出 [见公式 (3)] ,以能一致地测量距离。考虑所有这些项目的势场
得出 [见公式 (3)] ,以能一致地测量距离。考虑所有这些项目的势场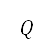 ,可表达如下
,可表达如下
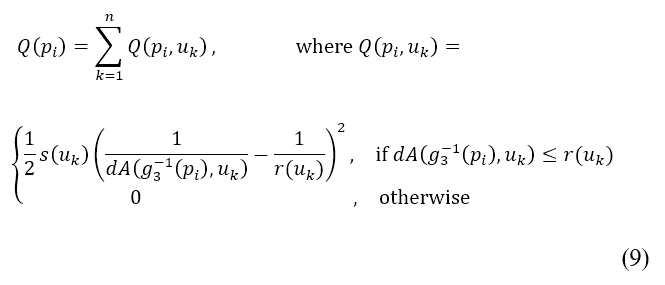
由于来源并不被视为障碍物,因此飞机的航道仍然可以越过其区域。换句话说,排斥势的大小,不应导致在航道规划中采用的代价函数在极限上接近零或无限大。透过将排斥势标准化至范围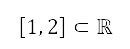 来加入这个限制,其中标准化的计算如下
来加入这个限制,其中标准化的计算如下
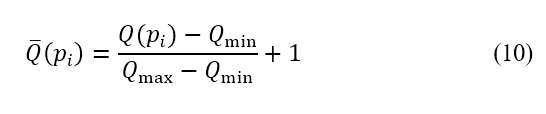
其中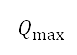 和
和 分别是整个势场最大和最小的排斥势值。根据上文提及与香港空域有关的例子,我们提出的势场是利用香港的人口数据来计算。图
4
左边显示了人口分布;而右边则显示了按照人口而计算的势场。右边显示的排斥势,在概念上是在各个来源中人口密度影响的叠加,并且是根据左边显示的人口分布计算出来。
分别是整个势场最大和最小的排斥势值。根据上文提及与香港空域有关的例子,我们提出的势场是利用香港的人口数据来计算。图
4
左边显示了人口分布;而右边则显示了按照人口而计算的势场。右边显示的排斥势,在概念上是在各个来源中人口密度影响的叠加,并且是根据左边显示的人口分布计算出来。
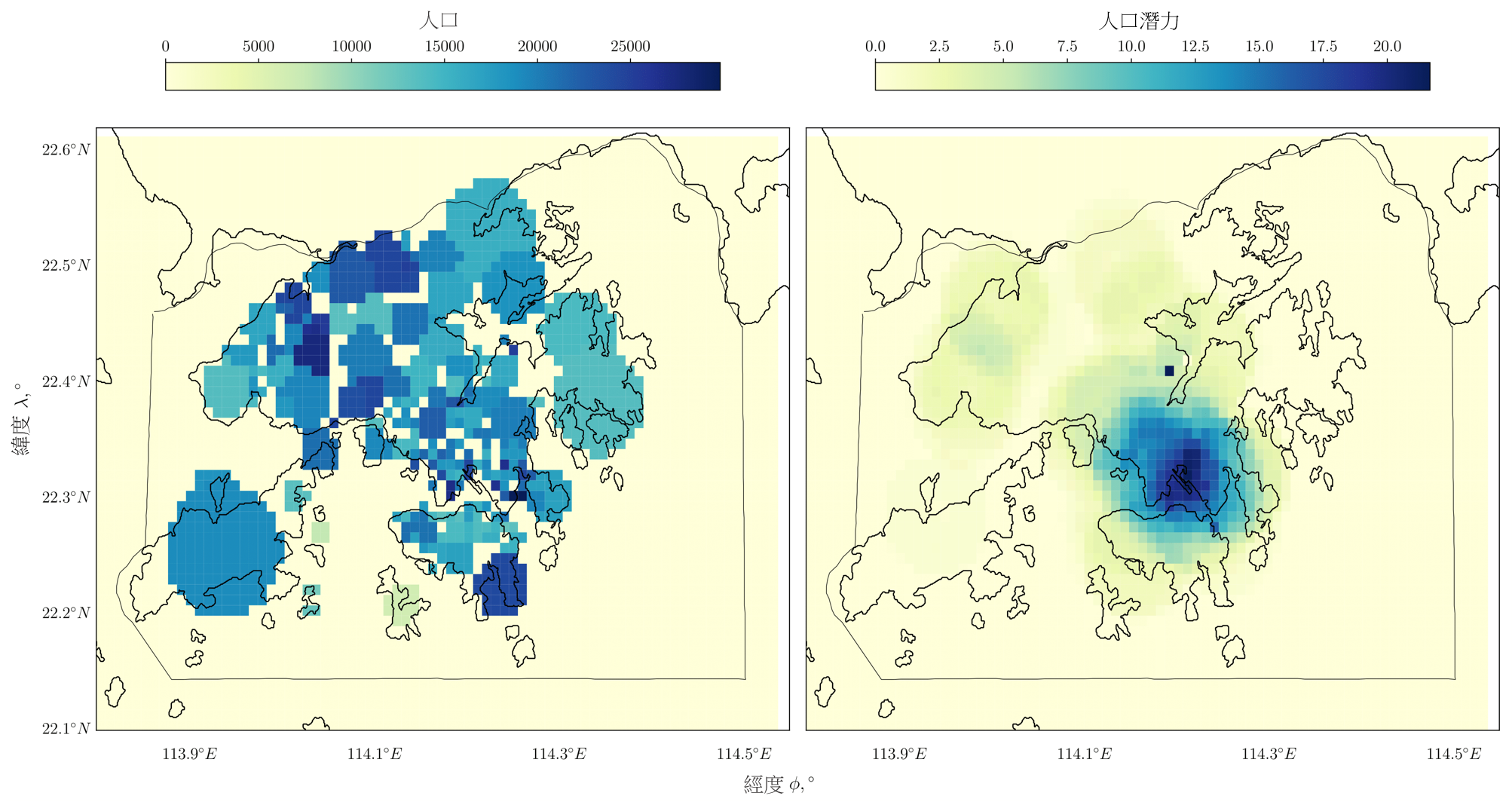
图 4:香港的人口分布(左)及使用公式 (9) 产生的相应势场表示(右)。
5. 包括考量人口因素及转向限制的后续离场阶段规划
在第 II.A.4 节说明的考量人口因素 A* 演算法中,透过公式(8)于当前节点位置得出最低代价函数 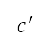 的航道,并透过测试八个方向的移动来搜寻下一个节点,如图 5
左边所示。这些移动方向受到网格节点的几何配置限制,并因此可能得出不符合物理要求的航道。为了解决这个问题,我们在制定的方法中定义了一个经改良的搜寻方向,其中包含以采样为基础的航道规划方法概念;图 5 的右边提供了一个例子。
的航道,并透过测试八个方向的移动来搜寻下一个节点,如图 5
左边所示。这些移动方向受到网格节点的几何配置限制,并因此可能得出不符合物理要求的航道。为了解决这个问题,我们在制定的方法中定义了一个经改良的搜寻方向,其中包含以采样为基础的航道规划方法概念;图 5 的右边提供了一个例子。
将 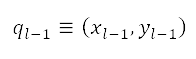 ,
, 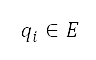 定为与航道中当前及下一个节点对应的点(以笛卡儿坐标表示)。为了增强航道的灵活性,在不同半径
定为与航道中当前及下一个节点对应的点(以笛卡儿坐标表示)。为了增强航道的灵活性,在不同半径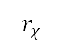 (其中
(其中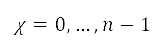 )的
)的 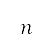 个同心圆的圆周上,我们在每一个角度区间
个同心圆的圆周上,我们在每一个角度区间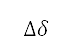 的
的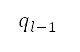 四周产生不同的样本点。图 5 右边说明了这个做法,其中
四周产生不同的样本点。图 5 右边说明了这个做法,其中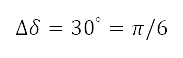 rad 及
rad 及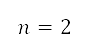 。为样本而产生的各点位置,以笛卡儿坐标
。为样本而产生的各点位置,以笛卡儿坐标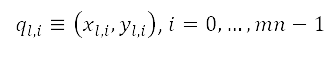 表示,计算方法如下
表示,计算方法如下
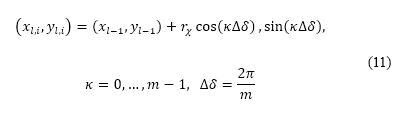
我们亦引入了一个用作限制航道角度变化的转向惩罚,其中考虑了飞机的横向适航性,并将这个透过抽样得出的转向惩罚纳入到考量人口因素 A* 方法中。我们将这种改良称为包含转向限制的考量人口因素 A* 方法。经改良的代价函数  表达如下
表达如下
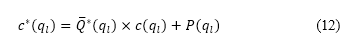
其中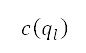 是上文提及的公式 (7) 中的代价函数,而经扩展的标准化势
是上文提及的公式 (7) 中的代价函数,而经扩展的标准化势 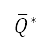 和转向惩罚
和转向惩罚 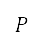 将会在下文说明。我们将
将会在下文说明。我们将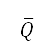 的领域(亦即在公式 (10) 中于
的领域(亦即在公式 (10) 中于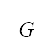 上定义的标准化排斥势)透过与
上定义的标准化排斥势)透过与 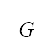 中节点
中节点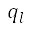 in
in 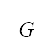 相邻的四个点上,计算标准化势的双线性插值,来扩展了至
相邻的四个点上,计算标准化势的双线性插值,来扩展了至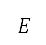 领域。我们以
领域。我们以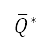 来表示这个扩展,以用来计算公式 (12) 的代价函数。
来表示这个扩展,以用来计算公式 (12) 的代价函数。
只有上一条航道和下一条航道之间的角度差 η 大于指定的角度区间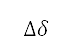 (用作圆形搜寻方向的区间)时,才应用位于
(用作圆形搜寻方向的区间)时,才应用位于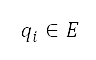 点的转向惩罚
点的转向惩罚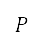 ,以避免航道角度急剧变化。惩罚权重
,以避免航道角度急剧变化。惩罚权重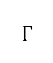 会根据起始节点到目标节点的距离加以调整。当上一个航道角度和下一个航道角度之间的差异增加时,惩罚便会增加,表达如下
会根据起始节点到目标节点的距离加以调整。当上一个航道角度和下一个航道角度之间的差异增加时,惩罚便会增加,表达如下
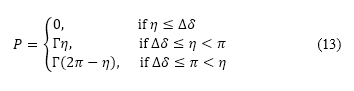
某程度上,当考虑飞机的适航性时,这个惩罚会作为一个惯性力。由公式 (12) 估算出的最低成本点,会在各个样本点中选取为航道上的下一个节点,这个过程会一直重复,直至飞机到达目标为止。
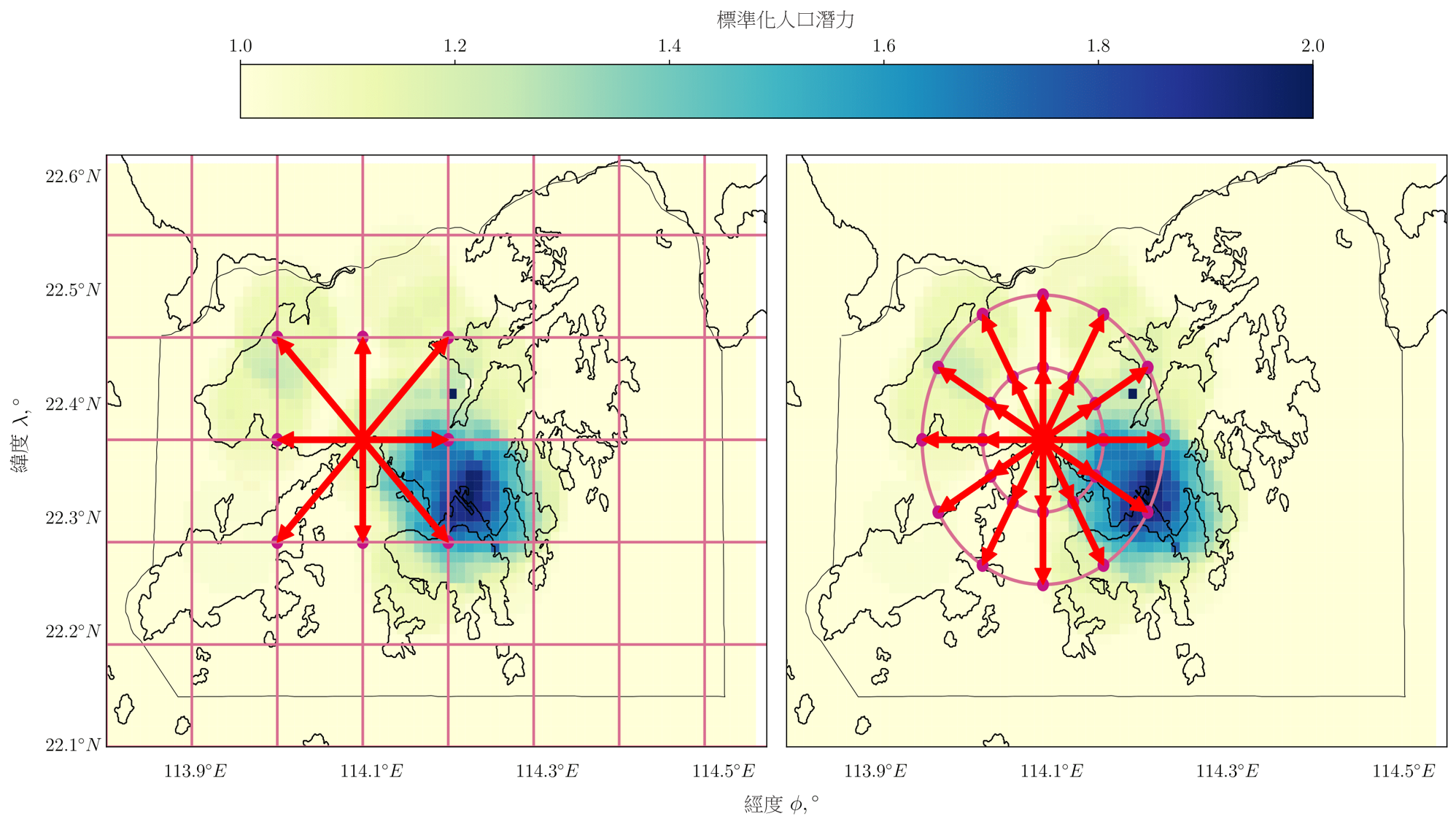
图 5:A*演算法及考量人口因素 A* 方法在网格上的八个可能移动方向(不按比例)(左)及
在包含转向限制方法下,考量人口因素 A* 的 24 个可能移动方向(右)
B. 高度航道规划
第 II.A 节说明的地平面航道规划方法,在考虑禁飞区、跑道角度、机场附近的飞机飞机间隔、人口密集地区及转向限制下,确定了从离场机场到强制位置报告点的最短地平面航道。我们制定的高度航道规划方法,透过估计航迹沿途的燃料消耗及累积的感知到的噪音水平,以沿著产生的地平面航道显示出一条完整的三维航道。在第 II.B.1 节,我们提出一个能将这条航迹沿途的燃料消耗和噪音水平减到最低的优化构思。第 II.B.2 节解释一个纵向的模拟飞行方法,以在计算相应的燃料消耗量时产生前往目标的飞行航道。第 II.B.3 节说明用作估算沿著这条飞行航道的噪音水平的方法。
1. 优化问题的构思
本研究提出了两个高度航道的构思,分别是单变量优化及多变量优化,视乎沿著航道的高度上限是否改变而定。我们透过图 6 来说明这两个构思。举例而言,假如有一部飞机从香港国际机场出发(在图 6a 中以粉红色星号标示),这部飞机必须飞过其中一个强制位置报告点(以黑色三角形标示),这是我们航道规划方法的一个目标。根据 AIP 规定,深蓝色区域的航行高度层上限为 25,000 英尺。我们使用单变量构思以规划从香港国际机场前往这区域内报告点的航道,如 BEKOL、TAMOT 和 SIERA(如图 6a 的蓝色文字所示)。另外,我们构思了优化多变量问题,以因应从香港国际机场前往在航行高度为「地平面至无限」(AIP 所采用的术语,表示其高度不设上限,在图 6a 中以灰色区域表示)区域上的点来规划航道。表 1 总结了两种构思的详情,并会在下文加以说明。
我们假设单变量优化所产生的高度航道,是由两个飞行航段组成:起飞及加速爬升,如图 6b 所示。图中的起飞和加速爬升航段,分别与地平面航道的初步及后续离场阶段对应。我们透过模拟的第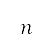 n 个时间步长来隐含地确定俯仰角
n 个时间步长来隐含地确定俯仰角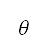 、高升力装置的配置
、高升力装置的配置 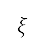 及油门因子
及油门因子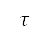 ,以及根据距离
,以及根据距离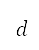 ,以及根据距离
,以及根据距离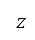 及速度
及速度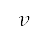 为每个航行段明确地加入边界条件,来进行确定航道的模拟飞行(在第 II.B.2
阐述)。从地平面航道的初步及后续离场,得出到达起飞及加速爬升航段终点的距离
为每个航行段明确地加入边界条件,来进行确定航道的模拟飞行(在第 II.B.2
阐述)。从地平面航道的初步及后续离场,得出到达起飞及加速爬升航段终点的距离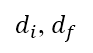 。视乎飞机类型和承载情况,在起飞终点的高度
。视乎飞机类型和承载情况,在起飞终点的高度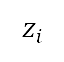 和速度
和速度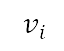 均为固定。而加速爬升终点的目标高度
均为固定。而加速爬升终点的目标高度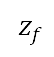 ,是单变量优化的设计变量,如表 1
第二列所示。目标高度的改变会导致与引擎动力和飞机速度等操作条件有关的垂直飞行剖面出现变化。这些条件会进一步令累积的感知到的噪音水平
,是单变量优化的设计变量,如表 1
第二列所示。目标高度的改变会导致与引擎动力和飞机速度等操作条件有关的垂直飞行剖面出现变化。这些条件会进一步令累积的感知到的噪音水平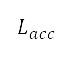 及燃料消耗量
及燃料消耗量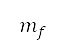 改变。因此,我们因应目标高度将燃料消耗及累积的感知到的噪音降至最低,如表 1
所示。在不同航行高度层边界之间切换的飞行航道,透过多变量优化来模拟,如表 1 第三列所示。假设这条航道有五个航段(如图 6c
所示):起飞、加速爬升、恒定校正空速(CAS)爬升,以及恒定马赫数爬升和巡航。在多变量优化中的起飞航段亦与地平面航道的初步离场阶段对应,而其余航段则于地平面航道的后续离场阶段对应。除了目标点的高度外,我们亦将在切换点
改变。因此,我们因应目标高度将燃料消耗及累积的感知到的噪音降至最低,如表 1
所示。在不同航行高度层边界之间切换的飞行航道,透过多变量优化来模拟,如表 1 第三列所示。假设这条航道有五个航段(如图 6c
所示):起飞、加速爬升、恒定校正空速(CAS)爬升,以及恒定马赫数爬升和巡航。在多变量优化中的起飞航段亦与地平面航道的初步离场阶段对应,而其余航段则于地平面航道的后续离场阶段对应。除了目标点的高度外,我们亦将在切换点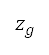 的巡航马赫数
的巡航马赫数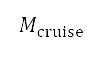 及高度视为设计变量。这个在航道上的切换点位于图6a 中蓝色与灰色区域之间的边界,当中航行高度上限会从
25,000 英尺切换至无限。我们将这个点设定在加速爬升航段的终点,同时亦考虑了这个点的其他边界条件(如高度、距离和速度)。如上文所述,这个点的高度是其中一个设计变量。前往这个点的距离
及高度视为设计变量。这个在航道上的切换点位于图6a 中蓝色与灰色区域之间的边界,当中航行高度上限会从
25,000 英尺切换至无限。我们将这个点设定在加速爬升航段的终点,同时亦考虑了这个点的其他边界条件(如高度、距离和速度)。如上文所述,这个点的高度是其中一个设计变量。前往这个点的距离 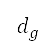 是透过 AIP 来确定的。由于加速爬升后的后续航段属于恒定速度类型(恒定的 CAS
或马赫数),同时巡航马赫数是其中一个设计变量,因此在切换点的速度
是透过 AIP 来确定的。由于加速爬升后的后续航段属于恒定速度类型(恒定的 CAS
或马赫数),同时巡航马赫数是其中一个设计变量,因此在切换点的速度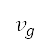 ,是按以下公式由在切换点的巡航马赫数和高度来确定:
,是按以下公式由在切换点的巡航马赫数和高度来确定:
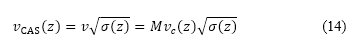
其中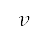 是真正的空速,
是真正的空速,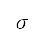 是密度比,而
是密度比,而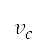 是音速。我们假设当等量空速等于校正空速
是音速。我们假设当等量空速等于校正空速 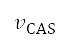 。在表 1,带有星号的符号表示上文因应模拟飞行方法而解释的既定边界条件。AIP
提供了在强制位置报告点
。在表 1,带有星号的符号表示上文因应模拟飞行方法而解释的既定边界条件。AIP
提供了在强制位置报告点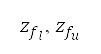 以及切换点
以及切换点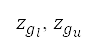 的航行高度下限及上限。巡航马赫数的变量限制于下马赫数和上马赫数
的航行高度下限及上限。巡航马赫数的变量限制于下马赫数和上马赫数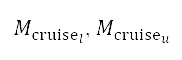 之间,是根据飞机类型及其操作条件而定。高升力装置的配置及油门因子受限于区间
之间,是根据飞机类型及其操作条件而定。高升力装置的配置及油门因子受限于区间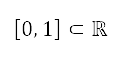 之间,
而俯仰角则受到起飞、爬升及巡航的适当操作条件所限制。用作解答这些单变量及多变量多目标优化问题的方法,是以非支配型排序基因遗传演算法 II(NSGA-II,是一种快速分类及精良的多目标遗传演算法)为基础 [40]。
之间,
而俯仰角则受到起飞、爬升及巡航的适当操作条件所限制。用作解答这些单变量及多变量多目标优化问题的方法,是以非支配型排序基因遗传演算法 II(NSGA-II,是一种快速分类及精良的多目标遗传演算法)为基础 [40]。
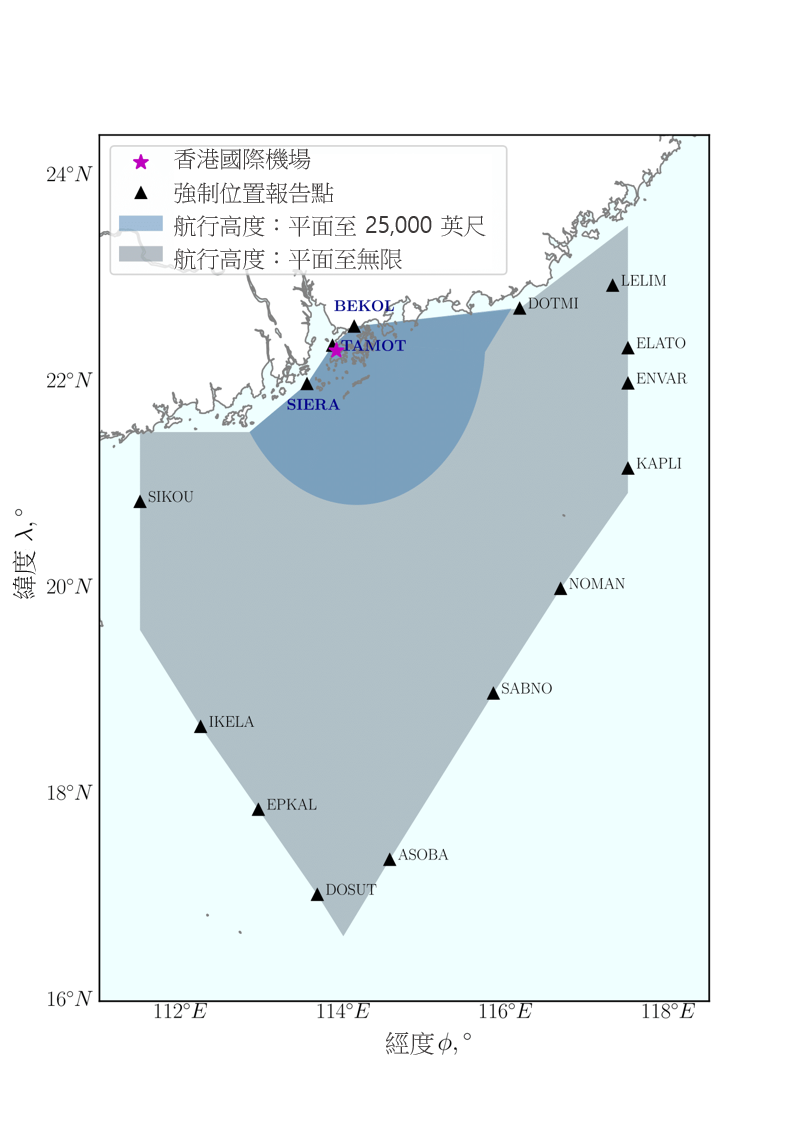 a) 香港空域的飞行高度限制
a) 香港空域的飞行高度限制
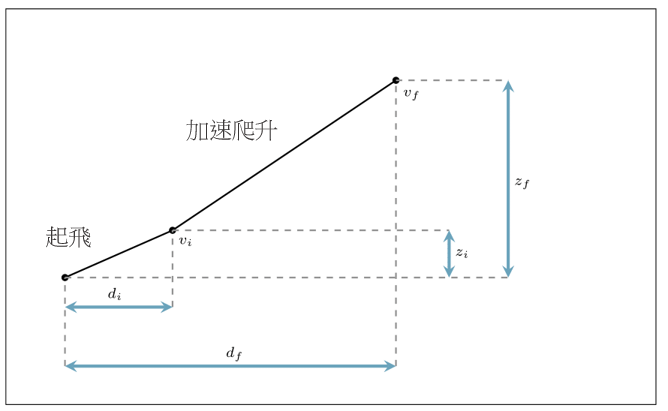 b) 单变量优化的航段(不按比例)
b) 单变量优化的航段(不按比例)
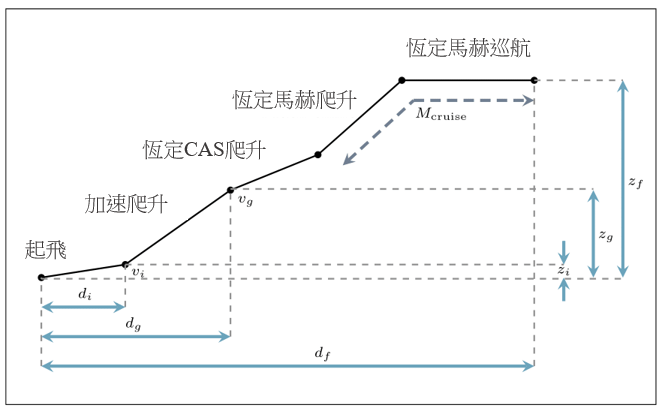 c) 多变量优化的航段(不按比例)
c) 多变量优化的航段(不按比例)
图 6:飞行高度限制图 a) 影响单变量及多变量优化的选择,及航段组合以模拟单变量优化的离场航道 b) 及多变量优化 c)
这个演算法会建立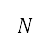 个包含设计变量的人口,并将透过交互和变异而产生的父母及后代结合起来。之后,我们会为这个人口估算目标,并且按它们的等级和挤拥距离以递增方式排列。这个等级表示了以显性为基础的解答层级次序。举例而言,在设计变量值
个包含设计变量的人口,并将透过交互和变异而产生的父母及后代结合起来。之后,我们会为这个人口估算目标,并且按它们的等级和挤拥距离以递增方式排列。这个等级表示了以显性为基础的解答层级次序。举例而言,在设计变量值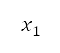 及
及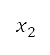 下,当
下,当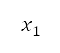 支配
支配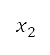 时,
时,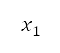 便会比
便会比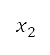 具有较高等级。在相应于
具有较高等级。在相应于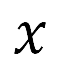 下将两个目标
下将两个目标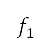 和
和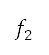 减到最低的优化问题中,其定义为
减到最低的优化问题中,其定义为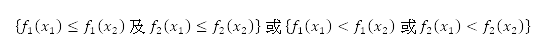 。挤拥距离表示解答的密度。假如两个解答属于同一等级,则位于密度较低区域的解答将获分配较高的优先次序。排序列表的前半部分会进化成后代,并组成下一代人口
。挤拥距离表示解答的密度。假如两个解答属于同一等级,则位于密度较低区域的解答将获分配较高的优先次序。排序列表的前半部分会进化成后代,并组成下一代人口
本研究采用了两个特点以提升优化过程的计算效率。首先,有别于探索连续领域的传统 NSGA-II,具有整数编程的 NSGA-II
会用作进行离散优化。虽然我们的设计变量是与连续的物理数量对应,但是考虑到其实际意义的离散性,则有助有效地探讨设计空间。举例来说,我们可以估算在目标巡航高度为 11,000.0 米及 11,000.1
米的噪音和燃料消耗,并在数学上得出其中一个条件较佳的结论,但对于航空运输航线而言,这没有实际意义。相反,我们利用相同的计算时间来估计目标高度为 11,000 米及 11,100
米的目标函数,以找出目标函数变量的概括趋势。为了考虑具有特定区间的设计变量,我们并没有采用离散优化中常用的二进制编码基因演算法,相反在 NSGA-II
中使用包含随机整数采样的实数编码基因演算法。当中所产生的设计变量值为整数,上下范围处于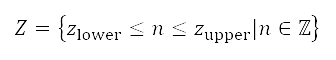 之间。由于设计变量值的数量有限,因此优化参数(例如人口规模和世代数目)会至少覆盖 20%
的设计空间。第二,动态编码中称为记忆化的技术,妨碍了估算重复设计变量的解答
[41]。透过储存燃料消耗和累积噪音的估算结果(透过进行费时的模拟飞行得出),此演算法能加快优化过程,并且在设计变量再次出现相同数值时提供已缓存的结果。
之间。由于设计变量值的数量有限,因此优化参数(例如人口规模和世代数目)会至少覆盖 20%
的设计空间。第二,动态编码中称为记忆化的技术,妨碍了估算重复设计变量的解答
[41]。透过储存燃料消耗和累积噪音的估算结果(透过进行费时的模拟飞行得出),此演算法能加快优化过程,并且在设计变量再次出现相同数值时提供已缓存的结果。
2. 燃料消耗估计量
我们采用了数据增强模拟飞行方法,以估计出高度航道沿途的燃料消耗 [42]。这个方法利用飞机初步设计阶段的可用资料以及各类型飞机的历史飞行数据,来产生纵向飞行航道以及估计燃料消耗量。早前,模拟飞行程序已根据短途、中途及长途航班的实际飞行数据加以验证,当中近似误差少于 7%。对于公式 (15) 中提出的移动控制公式,模拟飞行在固定边界条件下,为飞机位置和速度作为初值的问题得出了解答:
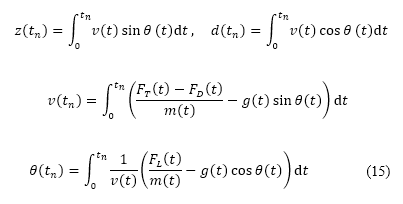
公式利用有限差值进行离散化,并在时间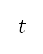 向前整合。我们将前往初步及后续离场阶段终点的距离
向前整合。我们将前往初步及后续离场阶段终点的距离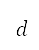 、速度
、速度 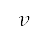 及高度
及高度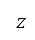 ,指定为地平面航道规划和优化设定中的边界条件。另外,我们亦指定了质量
,指定为地平面航道规划和优化设定中的边界条件。另外,我们亦指定了质量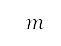 、速度、距离、高度和俯仰角的初值。之后,便使用这些初值来计算推力
、速度、距离、高度和俯仰角的初值。之后,便使用这些初值来计算推力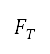 、升力
、升力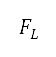 、阻力
、阻力 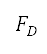 以及重力加速度
以及重力加速度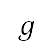 ,并将结果用来找出下一个时间步长的速度、俯仰角、距离和高度。当计算出来的速度、距离和高度符合后续离场阶段终点的要求时,便终止模拟,这表示总航行时间
,并将结果用来找出下一个时间步长的速度、俯仰角、距离和高度。当计算出来的速度、距离和高度符合后续离场阶段终点的要求时,便终止模拟,这表示总航行时间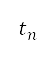 会受到边界条件影响。具体而言,本研究所使用的推力模型透过密度比
会受到边界条件影响。具体而言,本研究所使用的推力模型透过密度比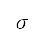 、马赫数
、马赫数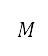 和油门因子
和油门因子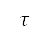 ,来考虑高度和速度的变化,如下所示
,来考虑高度和速度的变化,如下所示
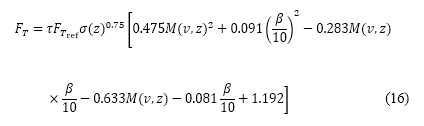
其中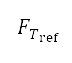 是飞机引擎的参照推力,而
是飞机引擎的参照推力,而 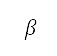 是其涵道比。所有参数均取决于引擎类型,并且假设为常数。马赫数和密度比是速度和高度的函数:
是其涵道比。所有参数均取决于引擎类型,并且假设为常数。马赫数和密度比是速度和高度的函数:
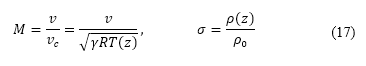
其中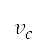 是音速,亦是空气热容比
是音速,亦是空气热容比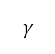 、气体常数
、气体常数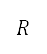 及大气温度
及大气温度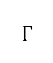 的函数。空气密度、压力和温度是由国际标准大气模型 [43] 确定。包括高度的引力加速度
的函数。空气密度、压力和温度是由国际标准大气模型 [43] 确定。包括高度的引力加速度 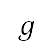 的变化,是透过地球形状的球面近似值计算。
的变化,是透过地球形状的球面近似值计算。
空气动力(升力 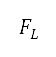 及阻力
及阻力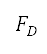 )会与空气密度、速度、机翼面积
)会与空气密度、速度、机翼面积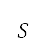 、升力系数
、升力系数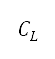 及阻力系数
及阻力系数 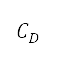 一并计算,表达如下:
一并计算,表达如下:
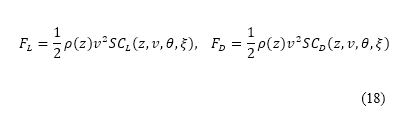
其中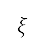 表示对高升力装置配置所作的修改。升力和阻力隐含地考虑了高度、速度、俯仰角和高升力装置配置。特别留意的是,升力系数是由
Polhamus 公式 [44] 及 Dubs 模型 [45]
确定,作为攻角(与本研究中的俯仰角相同)、马赫数(高度和速度的函数)、高升力装置配置,以及其他固定的飞机资料(例如机翼展弦比、机身阔度、掠角和翼展)的外显函数。阻力系数是由剖面阻力、触发阻力和波浪阻力的经验阻力累积方法来确定,作为升力系数、马赫数及其他飞机资料(例如机翼参照面积、机翼浸润面积、翼展、平均弦长、机身阔度、机身尾锥长度、机舱长度及机翼展弦比)的外显函数
[46]。透过解构以下子问题,便可确定模拟中每个时间步长的俯仰角、高升力装置配置以及油门因子的值:
表示对高升力装置配置所作的修改。升力和阻力隐含地考虑了高度、速度、俯仰角和高升力装置配置。特别留意的是,升力系数是由
Polhamus 公式 [44] 及 Dubs 模型 [45]
确定,作为攻角(与本研究中的俯仰角相同)、马赫数(高度和速度的函数)、高升力装置配置,以及其他固定的飞机资料(例如机翼展弦比、机身阔度、掠角和翼展)的外显函数。阻力系数是由剖面阻力、触发阻力和波浪阻力的经验阻力累积方法来确定,作为升力系数、马赫数及其他飞机资料(例如机翼参照面积、机翼浸润面积、翼展、平均弦长、机身阔度、机身尾锥长度、机舱长度及机翼展弦比)的外显函数
[46]。透过解构以下子问题,便可确定模拟中每个时间步长的俯仰角、高升力装置配置以及油门因子的值:
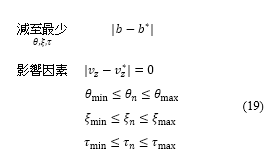
其中目标函数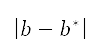 中的变量
中的变量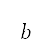 的类型取决于航段类型:起飞和加速爬升航段时,变量
的类型取决于航段类型:起飞和加速爬升航段时,变量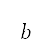 是
是 方向加速度;恒定 CAS 爬升航段时,变量
方向加速度;恒定 CAS 爬升航段时,变量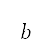 为校正空速;恒定马赫爬升及巡航段时,变量
为校正空速;恒定马赫爬升及巡航段时,变量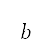 为马赫数。而
为马赫数。而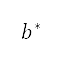 是与每个属性对应的所需值,是由边界条件隐含地确定。因此,将
是与每个属性对应的所需值,是由边界条件隐含地确定。因此,将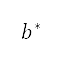 和
和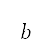 之间的绝对差异减至最少,会迫使属性在相应的航段中保持为常数。同样地,对每个航段而言,垂直速度
之间的绝对差异减至最少,会迫使属性在相应的航段中保持为常数。同样地,对每个航段而言,垂直速度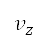 亦是一个常数,而目标垂直速度
亦是一个常数,而目标垂直速度 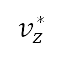 则由 [42]
所展示的数据分析来确定。每个设计变量都受限于其各自的最小值和最大值,在变量范围内用下标「min」和「max」表示,并会因航段类型而各有不同。我们只会在起飞和加速航段(期间会展开襟翼和缝翼)中,考虑高升力装置配置。
则由 [42]
所展示的数据分析来确定。每个设计变量都受限于其各自的最小值和最大值,在变量范围内用下标「min」和「max」表示,并会因航段类型而各有不同。我们只会在起飞和加速航段(期间会展开襟翼和缝翼)中,考虑高升力装置配置。
燃料消耗量是采用以下公式的离散形式计算
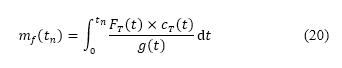
这取决于模拟中每个时间步长的推力、重力加速度及具体的燃料消耗量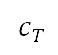 。具体燃料消耗量是使用从引擎数据集(透过开源资料库Surrogate Modelling
Toolbox(SMT)[47]
取得)所建立的代理模型来确定的,并视乎高度、速度和油门因子而定。
。具体燃料消耗量是使用从引擎数据集(透过开源资料库Surrogate Modelling
Toolbox(SMT)[47]
取得)所建立的代理模型来确定的,并视乎高度、速度和油门因子而定。
3. 累积感知到的噪音水平估计
我们使用了 Eurocontrol 飞机噪音及性能(ANP)数据库‡‡中的噪音动力距离(NPD)表来估算累积感知到的噪音水平。ANP/NPD 数据库是一个网上数据资源,用作估计由飞机所触发的噪音影响,当中展示了各种不同的飞机类型、操作和声学模型,并且提供了 ECAC Doc. 29 及 ICAO Doc. 9911 指导文件 [48,49]。
针对感知到的噪音水平,我们使用了 ANP 数据库中的 A
加权声曝水平模型,它代表了在一秒之内整合的总声音能量,是按照人类耳朵的灵敏度而专门配置,并且会受到飞机类型、引擎推力、操作模式(例如离场或进场)以及飞机与观察者之间的距离所影响
[50]。为航道规划而选择的飞机将类型定为常数。另外,由于我们在本研究中只考虑离场航道规划,因此操作模式亦是一个常数。引擎推力和距离以第 II.B.2
节中说明的模拟飞行来确定。在我们的研究中,由于是假设观察者是处于飞机下方海平面的地面上;因此与观察者之间的距离相等于高度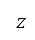 。高度航道沿途的累积感知到的噪音水平,可从以下表达式得出:
。高度航道沿途的累积感知到的噪音水平,可从以下表达式得出:
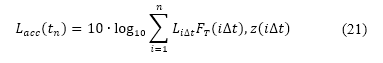
其中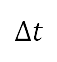 是模拟飞行中使用的时间步长,如第 II.B.2 节所述,而
是模拟飞行中使用的时间步长,如第 II.B.2 节所述,而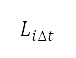 是第
是第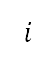 个时间步长的 A 加权声曝水平 。由于累积的声曝水平显著受到对数和所导致的最大
个时间步长的 A 加权声曝水平 。由于累积的声曝水平显著受到对数和所导致的最大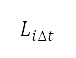 所影响,因此我们在优化过程中只考虑爬升航段的声曝水平,从而能清晰地观察改变高度航道对累积噪音水平所产生的影响。
所影响,因此我们在优化过程中只考虑爬升航段的声曝水平,从而能清晰地观察改变高度航道对累积噪音水平所产生的影响。
III. 结果及讨论
本节说明地平面航道规划的结果,以及沿著香港至伦敦及香港至台北(本文所采用的两个研究个案)这两条航线所得出的一组最佳高度航道。模拟飞行的参数是以配备了 GE90-115B 引擎的波音 777-300ER 客机为依据。第 II 节说明由我们制定的航道规划和优化过程,适用于从香港国际机场(北纬 22°18'32.0'',东经 113°54'52.0'')越过强制性 ATS 位置报告点的航班,即前往伦敦希斯路机场的飞机为 BEKOL (北纬 22°32’36.0’’,东经 114°08’00.0’’);前往台湾桃园国际机场为 ENVAR(北纬21°59’29.8’’N,东经 117°30’00.0’’)。
A. 地平面航道规划
在本节,我们采用第 II A 节中的方法,为香港至伦敦的航线(图 7)及香港至台北的航线(图 8)产生经优化的地平面航道。在讨论每条航线的具体结果前,我们会先描述图中所包括的标示方式。
图中的位置与香港国际机场对应,并以星号标示,当中香港国际机场是航道规划的起点。以黑色三角形标示的地点是强制性 ATS 位置报告点,是航道规划的目标点。以红色标示的区域是第 II.A.2 节所述的障碍物,飞机无法越过。黑线代表国家的边界及其海岸线。叠加的颜色代表标准化人口势场的强度。如第 II.A.4 节所述,深蓝色区域的人口密度高,不适合飞机飞越。相应的 SID 路径以粗灰线显示,与使用黑色轮廓圆圈标示的 SID 引导点连接。另外,以波音 777-300ER 航班的快速存取记录器(QAR)数据所产生的九条飞行航道,以紫色线显示。QAR 记录了飞机在飞行过程中的详细操作资料,例如位置、高度角、空速、重量等。在本研究中,QAR 数据中的经度、纬度、压力高度、推力及重量资料会用作比较和验证。航道规划结果会用四种颜色表示,以橙色显示的Dubins航道,是初步离场阶段(如第 II.A.3 所述)所产生的航道,亦是三条后续离场航道的共用航道。这三条航道的规划,即从Dubins航道终点至目标开始,会以「A*」、 「population-aware A*」及「population-aware A* with steering constraints」的名称表示。从这里起,为了方便易读,我们将这三种方法分别称为 A*、PA* 及 PA*S。
以蓝色显示的 A* 航道,是采用 A* 演算法得出的结果,当中只考虑第 II.A.2 节中提及的障碍物限制,并透过使用在公式 (7) 中表达的代价函数来产生这条航道。以绿色显示的PA* 航道,是采用第 II.A.4 节中提到的人口密集地区限制以及障碍物限制而得出的结果,并透过使用在公式 (8) 中表达的代价函数来产生这条航道。以洋红色表示的 PA*S 航道,是除了障碍物及人口密集地区限制外,亦采用了转向惩罚考虑因素而得出的结果,并透过使用在公式 (12) 中表达的代价函数来产生这条航道。PA*S 航道代表了本文所制定的地平面航道规划方法,当中在考虑到飞机的适航性及转向惩罚下,找出避开障碍物和人口密集地区的最短航道。
1.香港至伦敦
图 7 展示了飞机从香港国际机场起飞并前往伦敦希斯路机场的地平面航道规划。这条航线会越过由香港 AIS 指定的强制性 ATS 位置报告点 BEKOL。根据 BEKOL 的位置,我们选择图 2 中所示的 Departure 07R-1,作为这次模拟的初步离场航道。相对于飞往 BEKOL 的飞机,这个选择亦与我们对大部分 QAR 飞行航道数据的观察结果一致。使用 Departure 07R-1 至 BEKOL 的 SID 路径,是以连接 HKIA–ROVER–TUNG LUNG–ATENA–BEKOL 的线来表示。从香港国际机场开始的初步离场阶段,会在 ROVER 及 TUNG LUNG 线上的一个点结束。我们选择这个靠近人口密集地区作为结束点,目的是要观察透过不同规划方法所产生的航道会出现什么变化。后续离场阶段与从这点至 BEKOL 的航段对应。我们发现所产生的Dubins航道能符合初步离场航道限制,并且避开了机场四周的障碍物。
之后,在不考虑人口情况下 A* 演算法得出了越过香港内陆人口密集地区的最短航道。相反,PA* 和 PA*S 方法所产生的航线,避开了这个具有高度标准化人口势场的区域。在航道规划上,由于以笛卡儿坐标表示的 PA*S 比 PA* (只在网格点上运作)有更大自由度,因此当包含转向限制时,可观察到航向方向出现较小的急剧变化。
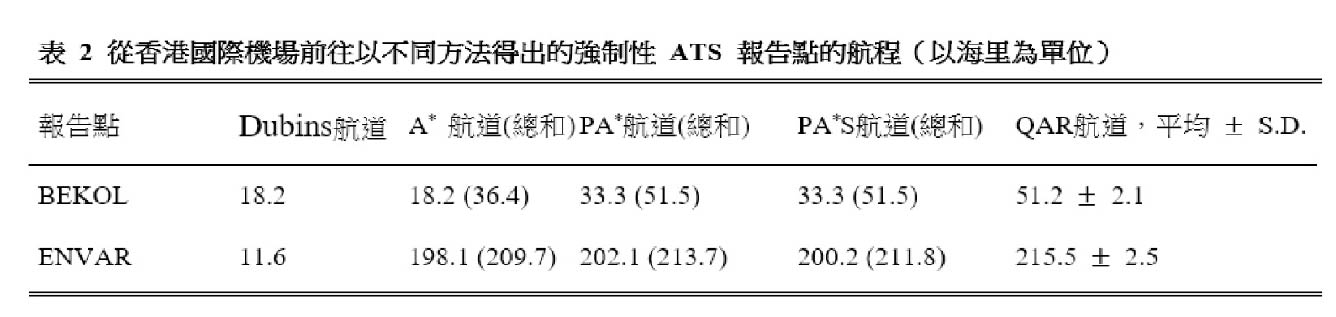
在三个结果中,包含Dubins航道的 PA*S 与 SID 路径及 QAR 航道最为相似,尤其是初步离场航道几乎与 SID 路径及 QAR 航道相同。从香港国际机场至 ROVER,被跑道角度限制的Dubins航道,几乎与 SID 路径和 QAR 航道平行。QAR 航道偏离Dubins航道以及 ROVER 和 TUNG LUNG 之间的 SID 路径,飞越人口密集的地区,并最终在 ATENA 越过香港东面的边陲地带飞往 BEKOL。当转向更接近 SID 引导点 TUNG LUNG 飞往 ATENA 时,与 QAR 航道比较下 PA* 航道更接近 SID 路径,显示我们所制定的方法有助于 SID 的规划。除了这个相似之处,可飞性亦可以由 PA*S 航道的初步及最终航道角来确定。在 TUNG LUNG 四周的初步航道角,由于按照著初步离场阶段终点的角度,因此航道稳定地朝向目标移动。在 BEKOL 附近,后续离场阶段终点的最终航道角与 QAR 航道的航道角相似,在作为验证上代表一条在物理上可飞行的航线。表 2 展示了透过每种航道规划方法而计算得出的航道长度,其中第一列表示在初步离场阶段中从Dubins航道计算得出的距离。随后三列代表使用本文提出的航道规划方法,在后续离场阶段计算得出的距离。在这些列中,括号「(总和)」中的航道长度是指在初步及后续离场阶段飞机所飞行的总距离,这是将透过从Dubins航道为这条航线得出的相应距离,与从每种方法得出的后续离场航道距离相加而计算出来。至于图 7 所示的九个 QAR 航道长度,最后一列显示了它们的平均值和标准偏差(S.D.)。为了评估我们的结果,我们将 A*、PA* 和 PA*S 航道的总长度,与 QAR 航道的平均长度进行比较。在这个个案中, QAR 航道的平均长度(51.2 海里)比 PA*S 航道的总长度(51.5 海里)短 0.3 海里。然而,值得留意的是 QAR 航道越过人口潜力高,而不是潜力低的地区。因此,PA*S 航道提供了一个经改良的解决方案,其中可避开人口密集的地区,因此在无需显著增加飞行距离之下,或有助降低噪音的影响。
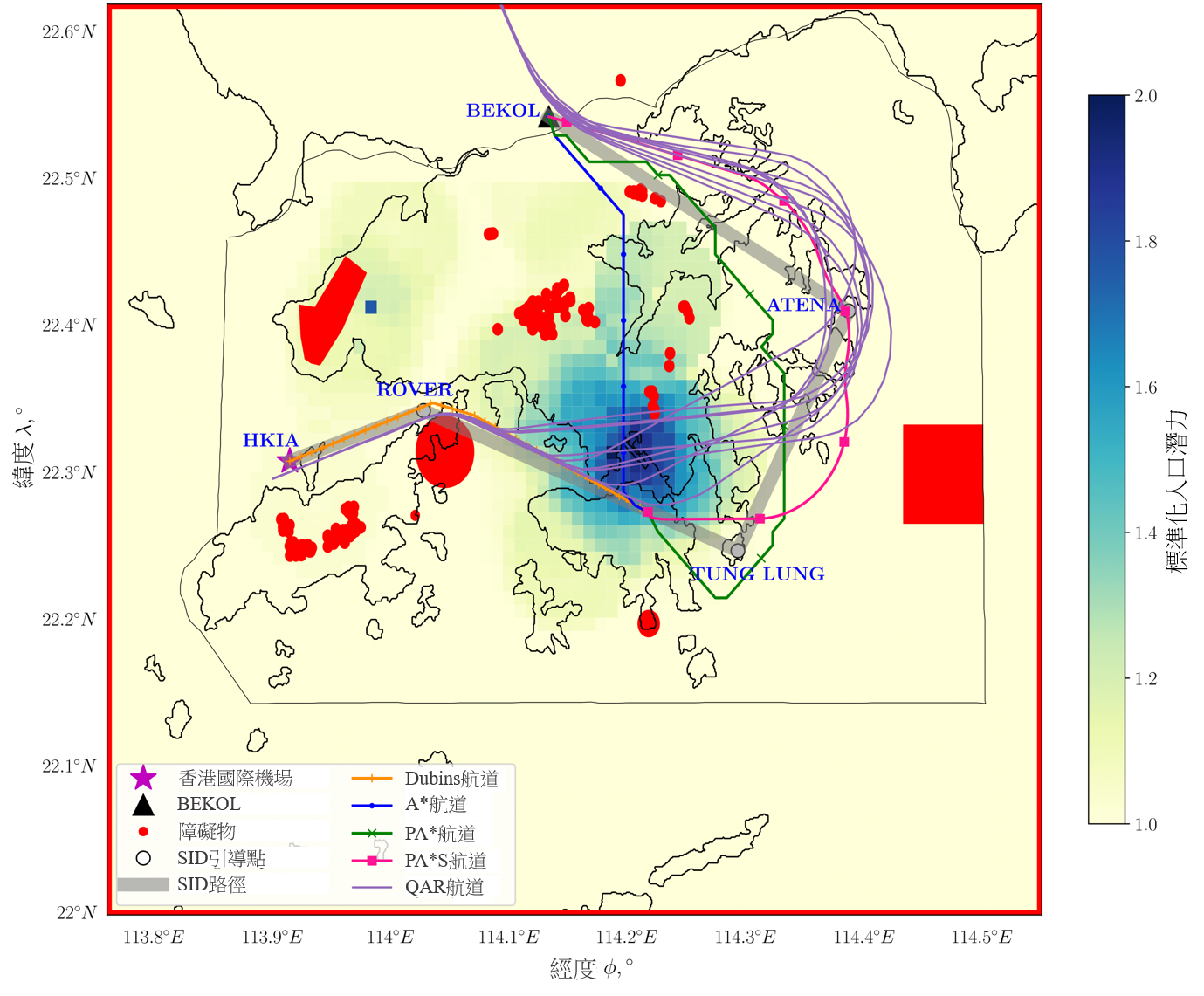
图 7:从香港国际机场至 BEKOL(香港至伦敦航线)的地平面航道,其中包含障碍物及香港空域下的标准化人口潜力
2. 香港至台北
图 8 展示了飞机从香港国际机场起飞前往台湾桃园国际机场的地平面航道规划。这条航线会越过同样是由香港 AIS 指定的强制性 ATS 位置报告点 ENVAR。由于目标点位于远离香港东南面的位置,因此我们将图 8 左边的图放大,而以香港地域为中心的图则在右边显示。飞往 ENVAR 的 SID 路径同样以灰色线显示,连接著 HKIA-ROVER-ROBBE-RAMEN-OCEAN-ENVAR。飞机的初步离场阶段是从香港国际机场飞往 ROBBE,使航道规划方法变得较为灵活,让其可沿著Departure 07R-1 或 07R-2 移动(见图 2)。后续离场阶段将从 ROBBE 移动至 ENVAR。在右边的放大图中,Dubins航道几乎与 SID 路径和 QAR 航道平行,符合初步离场航道的限制。之后,A* 演算法产生出一条与 Departure 07R-1 路径相似,并且越过高人口潜力地区的航道。相反,PA* 和 PA*S 方法则产生出与 Departure 07R-2 路径相似,并且倾向避开高人口地区的航线。
最短的 A* 航道仍然会沿著 Departure 07R-1 路径越过高人口潜力的地区。大约 70% 的 QAR 航道亦会越过这个区域,在噪音方面造成负面影响。余下跟随 Departure 07R-2 路径的 QAR 航道,则与 PA*S 和 SID 路径颇为相似。PA*S 航道在 RAMEN 和 OCEAN 之间偏离 SID 路径,如图中左边所示。这个偏差特别有助缩短航道的长度,如表 2 所示。对于这条航线,QAR 航道的平均飞行距离比 PA*S 航道的平均飞行距离长约 3 海里。这个差异主要是由于在 OCEAN 四周的大幅度转弯而造成,如图 8 所示。我们观察到部分 QAR 航道没有经过 OCEAN,导致航道与 PA*S 的航道相似。这个观察结果显示所产生的 PA*S 航道适合飞行。虽然我们的方法所产生的航线比大部分 QAR 航道短,但是却没有考虑某些航空运输的限制,例如包括有多架飞机在相似航线上飞行的空中交通情况。然而,有别于 PA*,PA*S 在 ROBBE 保持飞行方向,原因是转向限制的作用就如惯性力般,因此亦可以模拟当前的飞行操作,如 QAR 航道所示。此外,我们在受网格点限制的 A* 及 PA* 航道中所看到的急剧转弯,却未有在 PA*S 航道中发现。
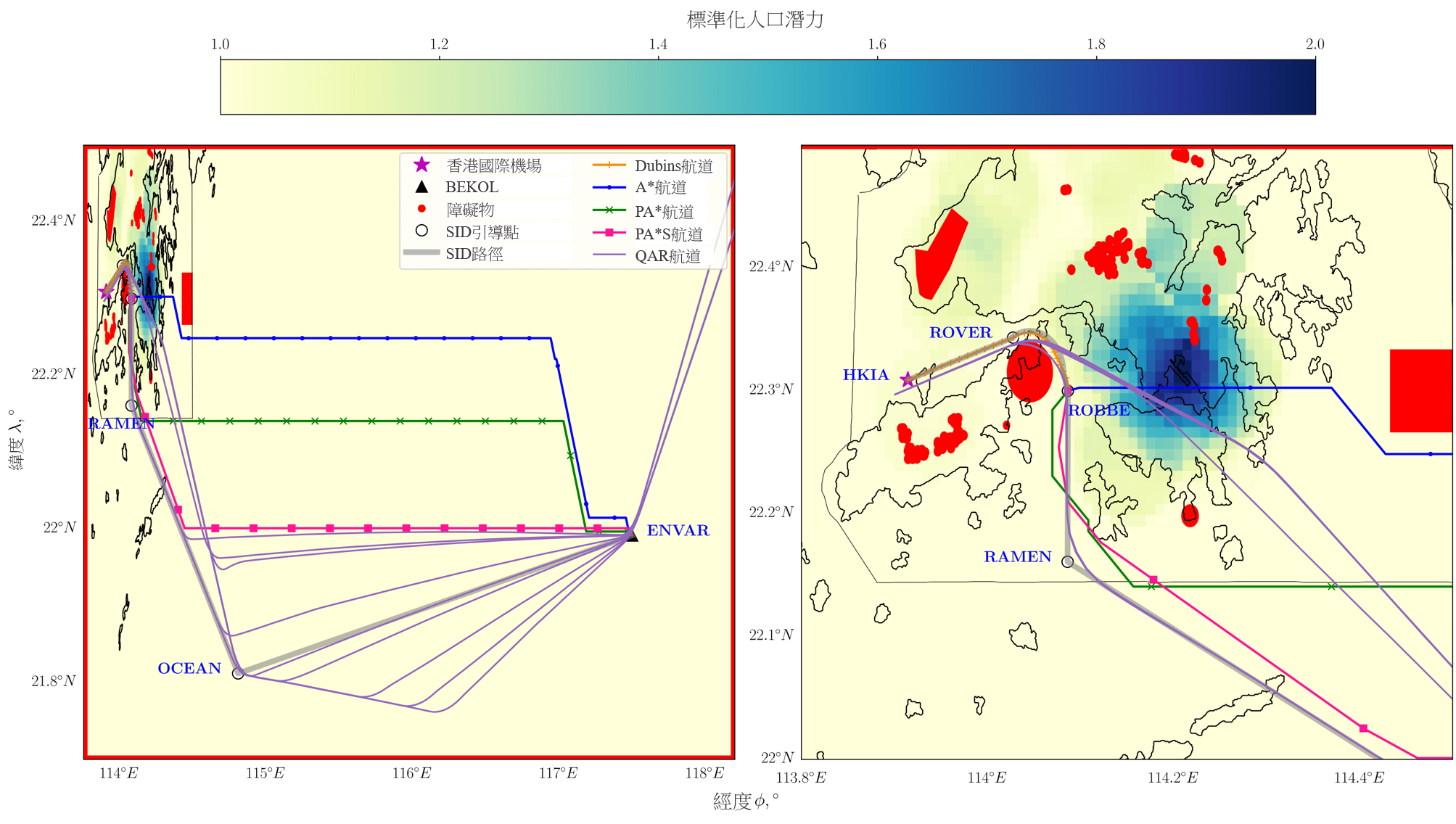
图 8: 从香港国际机场至 ENVAR(香港至台北航线)的地平面航道,其中包含障碍物及香港空域下的标准化人口潜力
B. 高度航道规划
我们透过进行低燃耗及低噪音影响的多目标优化,提出了在两种情境下的高度航道,如第 III.A 节所示。按照第 II.B. 节所描述的构思,从香港国际机场到 BEKOL 的航道,是透过单变量优化得出;而从香港国际机场到 ENVAR 的航道,则是以多变量优化取得。与意在规划出一条最短路径的地平面航道规划方法不同,我们希望能得出以多条高度航道作为多目标优化的一组解决方案。这些航道由图 9 左边和图 10 顶部的图表表示,其中横轴是飞行距离,纵轴是高度。图 9 右边和图 10 底部显示了优化的可行区域,以及低燃料消耗和低累积感知到的噪音水平的帕累托前沿。可行区域是指在优化过程中,由经修改的 NSGA-II 演算法所估算的所有解决方案。在图 9 中,这个区域以彩色地图显示,代表单变量优化的高度,而图 10 则以浅蓝色表示多变量优化。请留意,我们使用相同的颜色来标示图 9 右边优化解决方案的相应高度。在各个可行的解决方案中,非支配解决方案(即帕累托前沿)以实心的洋红色线和三角形表示。与地平面航道图一样,QAR 航道的高度变化以紫色虚线和紫色星号表示。图 9 左边和图 10 顶部的紫色星号,表示在各自航道中与相应的强制性 ATS 位置报告点最接近的点,而图 9 右边分别表示用作与解决方案进行比较的燃料消耗和噪音水平。
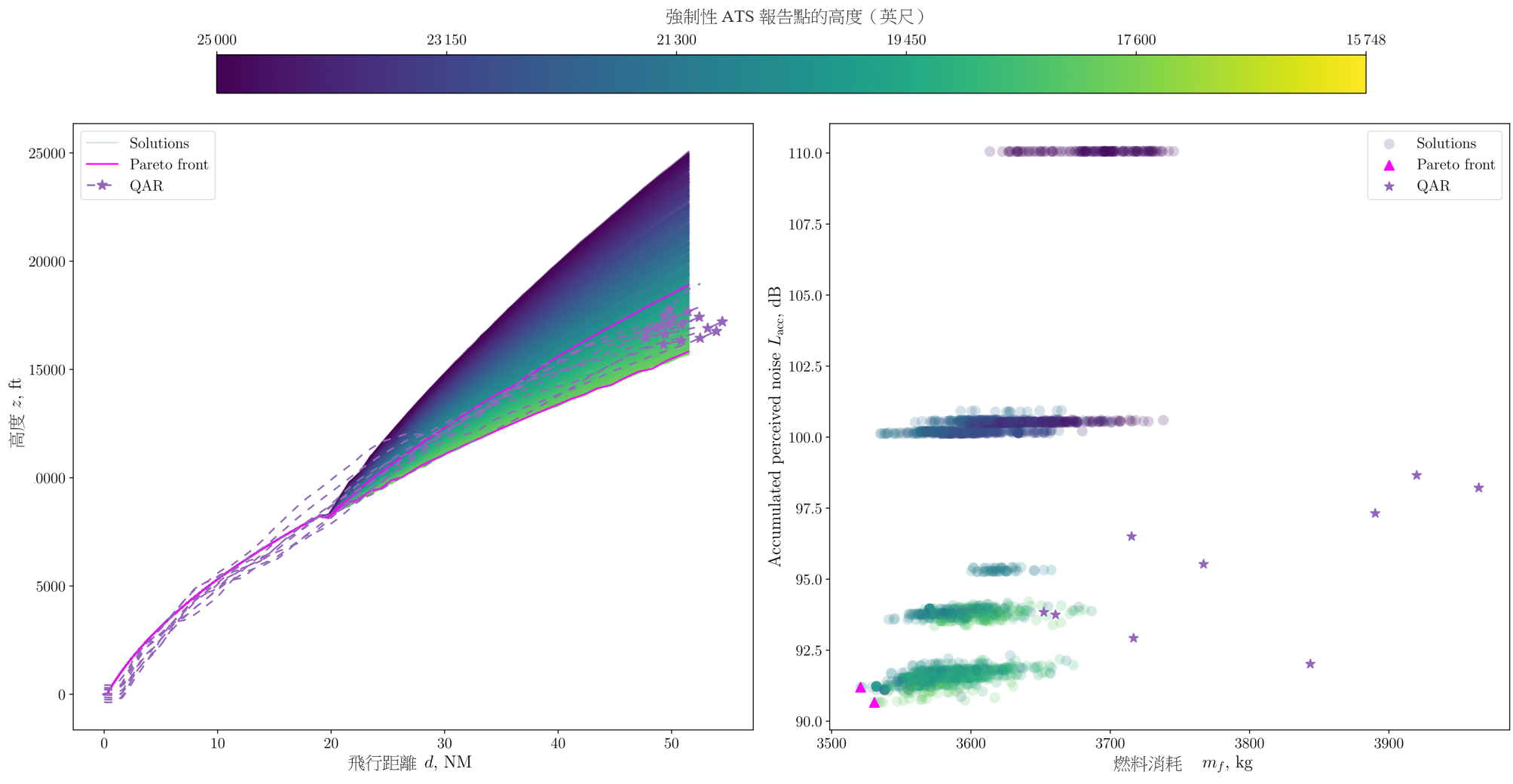
图 9:高度航道优化的可行解决方案、其帕累托前沿,以及从香港国际机场飞往 BEKOL 的 QAR 数据(左)
及相应的燃料消耗及渐强的感知噪音水平(右)
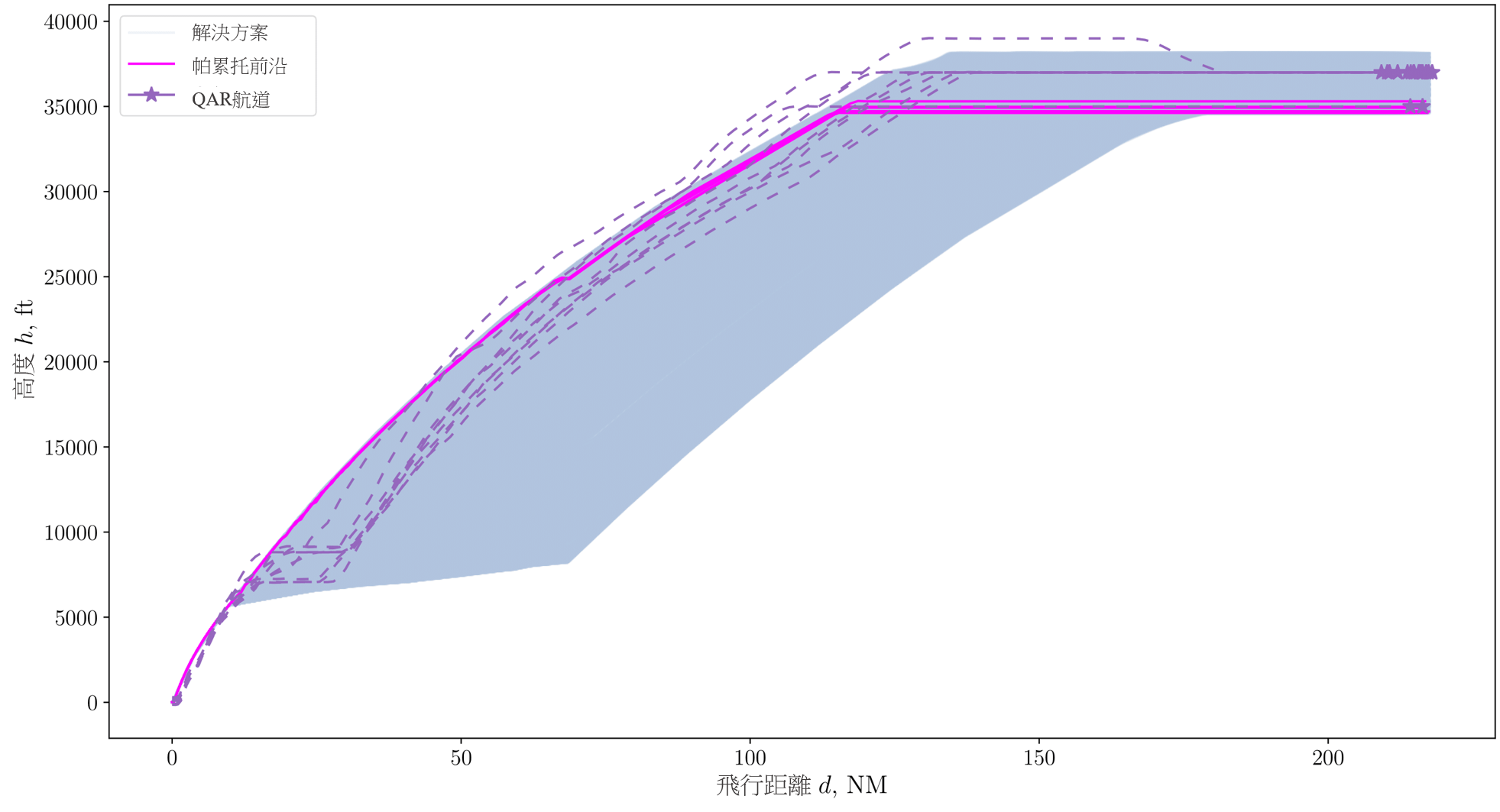
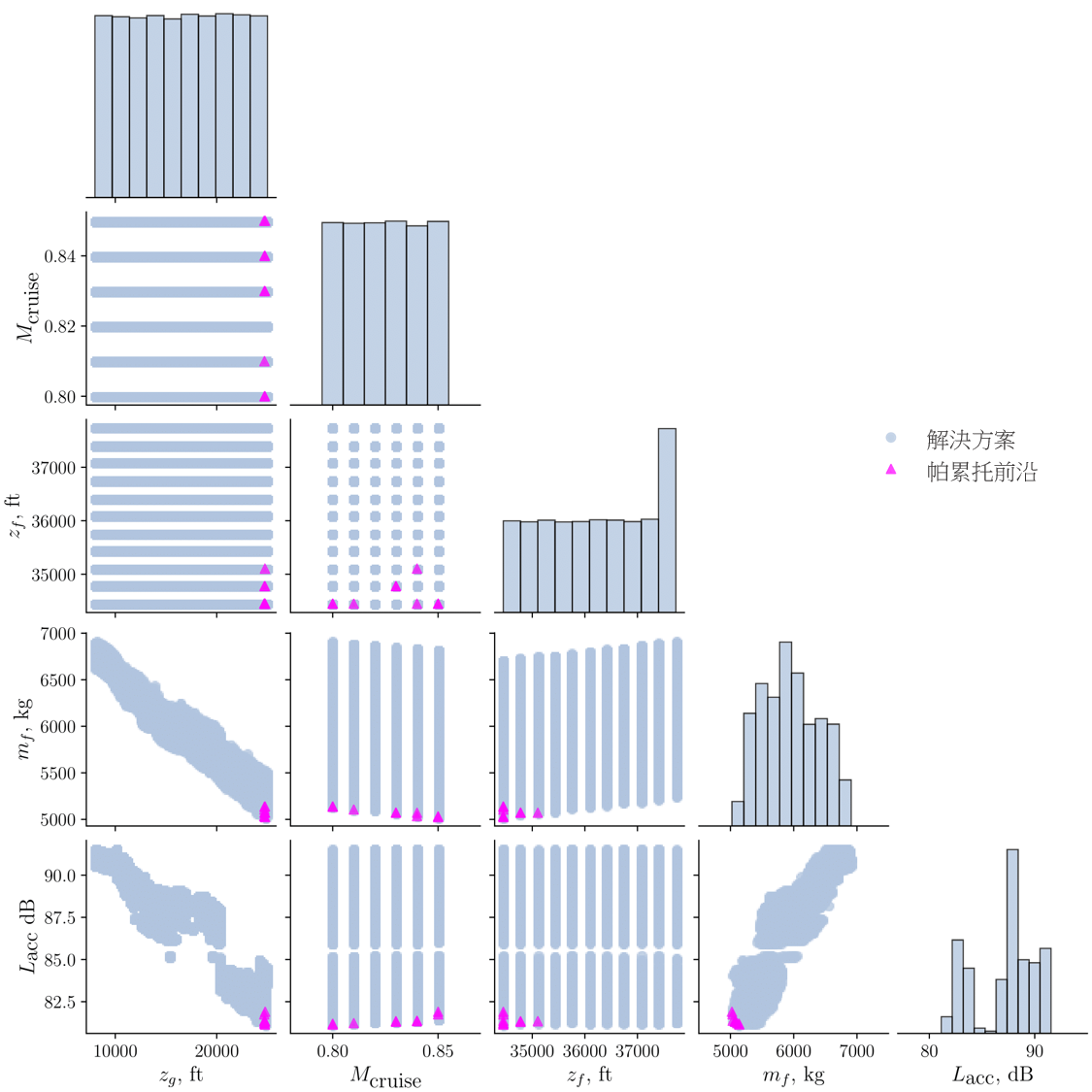
图 10:优化高度航道的可行解决方案、其帕累托前沿,以及从香港国际机场飞往 ENVAR 的 QAR 数据(上)及
与三个设计变量相关的燃料消耗和累积感知噪音水平,即目标高度、切换点高度及巡航马赫数(底)
高度航道由初步及后续离场航道组成,与地平面航道相似。图 9 左边及图 10 顶部只有一条洋红色线的航道,是与图 6b 及 6c
的起飞航段对应的初步离场航道,这是与地平面航道规划的Dubins航道部分对应。Dubins航道的飞行距离(如表 2 第二列所示),是起飞航段起点到终点的总距离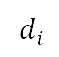 。后续离场航道的飞行距离
。后续离场航道的飞行距离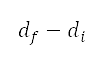 是 PA*S 航道的飞行距离,如表 2 第五列所示。我们将前往切换点
是 PA*S 航道的飞行距离,如表 2 第五列所示。我们将前往切换点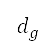 的飞行距离设定为 66 海里,这是从地平面航道规划及 AIP 中的资料中得出。
的飞行距离设定为 66 海里,这是从地平面航道规划及 AIP 中的资料中得出。
表 3 列出了我们使用的优化参数。在 NSGA-II 中基因演算法的世代数目和人口大小,是根据设计变量的数目及其范围内的数值数量(根据订明的区间而定)所确定的设计空间大小来设定的。对於单变量优化,BEKOL
目标高度的下限及上限设定为 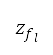 = 4,800 米 = 15,750 英尺,及
= 4,800 米 = 15,750 英尺,及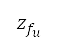 = 7,620 米 = 25,000 英尺(从 AIP 中取得)。优化以世代进化为 100 及人口大小为
20
进行,从中所产生的 2,000 个估计点,能够覆盖大部分设计空间,合共包含 2,821 个点。因此,我们认为世代数目和人口大小足以能具体地进行有关优化。至于多变量优化,ENVAR
的目标高度范围刚好是巡航高度,并设定为
= 7,620 米 = 25,000 英尺(从 AIP 中取得)。优化以世代进化为 100 及人口大小为
20
进行,从中所产生的 2,000 个估计点,能够覆盖大部分设计空间,合共包含 2,821 个点。因此,我们认为世代数目和人口大小足以能具体地进行有关优化。至于多变量优化,ENVAR
的目标高度范围刚好是巡航高度,并设定为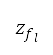 = 10,500 米 = 34,450 英尺,及
= 10,500 米 = 34,450 英尺,及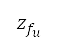 = 11,500 米 = 37,730
英尺,这是根据本研究中特定飞机类型的典型巡航高度而选择。这个高度范围与我们对飞行数据的观察结果一致。巡航高度范围的离散化区间设定为100 米,从而以较低的计算成本来估算设计空间的趋势。巡航马赫数
= 11,500 米 = 37,730
英尺,这是根据本研究中特定飞机类型的典型巡航高度而选择。这个高度范围与我们对飞行数据的观察结果一致。巡航高度范围的离散化区间设定为100 米,从而以较低的计算成本来估算设计空间的趋势。巡航马赫数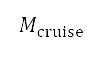 的范围,亦是根据我们在本研究中所选飞机的运作特性而设定:
的范围,亦是根据我们在本研究中所选飞机的运作特性而设定: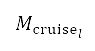 = 0.80 及
= 0.80 及 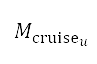 = 0.85。马赫数的离散化区间为
0.01。虽然在这些范围内的马赫数并非此离散化的整数,但是针对优化的设计变量抽样程序,我们将它们缩放成 80 至 85 之间的整数,其中的区间为 1,以能够进行整数编码。优化循环内的模拟飞行将这些整数设计变量,转换成介乎
0.80
和 0.85 之间,区间为 0.01 的适当物理数值。切换点
= 0.85。马赫数的离散化区间为
0.01。虽然在这些范围内的马赫数并非此离散化的整数,但是针对优化的设计变量抽样程序,我们将它们缩放成 80 至 85 之间的整数,其中的区间为 1,以能够进行整数编码。优化循环内的模拟飞行将这些整数设计变量,转换成介乎
0.80
和 0.85 之间,区间为 0.01 的适当物理数值。切换点 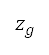 的高度范围设定为
的高度范围设定为 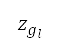 = 2,439 米 = 8,000 英尺,及
= 2,439 米 = 8,000 英尺,及 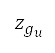 = 7,620 米 = 25,000 英尺。切换点高度变化的离散化区间为 1 米。多变量优化以世代进化为
700
及人口大小为 100 进行,覆盖20% 的设计空间,合共 342,012 个估算点。我们测试和调整了 NSGA-II 中的突变率和交互率,以适合进行本文所提出的优化。
= 7,620 米 = 25,000 英尺。切换点高度变化的离散化区间为 1 米。多变量优化以世代进化为
700
及人口大小为 100 进行,覆盖20% 的设计空间,合共 342,012 个估算点。我们测试和调整了 NSGA-II 中的突变率和交互率,以适合进行本文所提出的优化。

1. 香港至伦敦
图 9 左边显示了从香港国际机场至 BEKOL 的高度航道,并与在右边显示的燃料消耗及累积感知到的噪音水平对应。这里的累积噪音水平仅与第 II.B.3 节中提到的爬升航段对应。飞机的起飞重量设定为 3XX,XXX 公斤(根据与航空公司合作伙伴的协议,在出于保密原因下我们将数字屏蔽),这是根据 QAR 数据而得出的平均值。透过与本研究所使用的 QAR 数据进行比较,我们验证了燃料消耗及累积感知到的噪音水平的计算模型,其中燃料消耗和累积感知到的噪音水平的相对误差分别为 4.10% 和 2.34%,这为本研究所进行的优化带来充分的准确性。
如图 9 左边所示,在起飞和加速爬升航段结束时,结果符合地平面航道规划中Dubins和 PA*S 航道的飞行距离(如表 2 所示)。当中所产生的高度航道,其航迹与 QAR 航道非常相似。在右边,燃料消耗及感知到的噪音水平值的分布以颜色编码圆圈表示,作为模拟结果(亦即从 NSGA-II 优化产生的解决方案),而 QAR 航道的相关分布则以紫色星号显示。在与 QAR 航道相比下,高度航道图显示与模拟结果对应的高度显著地分布得更为广阔。然而,值得留意的是,正如在 QAR 航道的终点所观察的一样,在实际飞行中前往 BEKOL 的总距离与模拟结果有所分别。虽然 QAR 航道的分布更靠近右边,显示有较多的燃料消耗,但是模拟结果得出的显著高度变化以及 QAR 航道的飞行距离变化,却得出了相似的燃料消耗分布范围(约为 300 公斤)。
表 4 显示了与图 9 右边帕累托前沿集对应的 ATS 位置报告点的高度,以及对应的燃料消耗和累积的感知到的噪音水平。将噪音减到最低的航道目标高度为 15,458 英尺,在图 9 右边以洋红色的底部三角形表示。图 9 左边显示了相应的航道,其最终高度比 QAR 航道的高度低。将燃料消耗减到最低的航道目标高度为 18,917 英尺,在图 9 右边以洋红色的靠左三角形表示。图 9 左边显示了相应的航道,其最终高度高于QAR 航道的高度。噪音水平方面,我们观察到在一般情况下,随著右图纵轴的值增加,颜色会从黄色变成深蓝色,这表示随著目标高度增加,噪音水平亦会增加。
这个趋势是由于爬升到更高的目标高度需要更大的引擎动力输出而造成的,并且会相应地影响感知到的的噪音水平。然而,当目标高度大约为 16,400 英尺时,这个趋势便会逆转,其中在一组黄色圆圈下方噪音最低点附近,可以观察到一组绿色圆圈。对于这个特定区域的航道(即噪音趋势逆转的区域),飞机增加升力以到达更高的高度并非透过增强引擎动力,而是透过调整攻角或使用高升力装置。因此,我们可以利用类似的引擎动力水平以及与地面的更高距离,来降低噪音水平(在我们模型中,噪音水平是引擎动力和距离的主要函数)。同样地,随著横轴数值增加,颜色会由黄色变成深蓝色,表示随著目标高度增加,燃料消耗亦会增加。然而,透过更仔细的分析,我们可以看出飞机在处于最高高度时会消耗最多的燃料,而在最低高度却不表示燃耗最低。其中的转折点位于大约 19,000 英尺的高度,与燃耗最低点接近。帕累托前沿位于这个转折点附近,令优化结果得到验证。我们发现由于设计空间受到用作产生离散设计变量而订明的区间所限制,因此帕累托前沿集的基数可能很小。

2.香港至台北
图 10 顶部显示了从香港国际机场到 ENVAR 的高度航道,而底部则显示了包括设计变量的相应燃料消耗及累积感知到的噪音水平。这里的累积感知到的噪音水平亦仅与爬升航段对应。飞机的起飞重量设定为 2XX,XXX 公斤(因保密原因而屏蔽),这是基于 QAR 数据的平均值。顶部的航道图显示了在起飞结束时Dubins航道的飞行距离,以及加速爬升结束时 PA*S 的飞行距离,并且符合恒定的马赫数巡航段。
图中显示由模拟生成的可行起飞高度航道,与 QAR 航道几乎相同,同时起飞期间 QAR 航道的变化很小。主要差异出现在起飞接近结束时,其中在后续的爬升阶段前,大部分 QAR 航道在短时间内均保持水平飞行,这在我们的高度航道构思中并未加以考虑。虽然模型存在这种差异,但是对于在优化中所产生的可行解决方案,大部分 QAR 航道仍处于当中的操作范围内(浅蓝色区域)。我们观察到在这个短暂的水平飞行阶段后,各个 QAR 航道的爬升角会急剧增加。在这个阶段,航道会依循与高爬升率解决方案相似的模式,同时亦与帕累托前沿集的航道相似。这种模式在爬升阶段结束时会偏离至两个高度:在约 37,000 英尺及约 35,000 英尺的高度巡航。这些高度亦在解决方案的操作范围内,而帕累托前沿集则分布在 35,000 英尺的巡航高度附近。
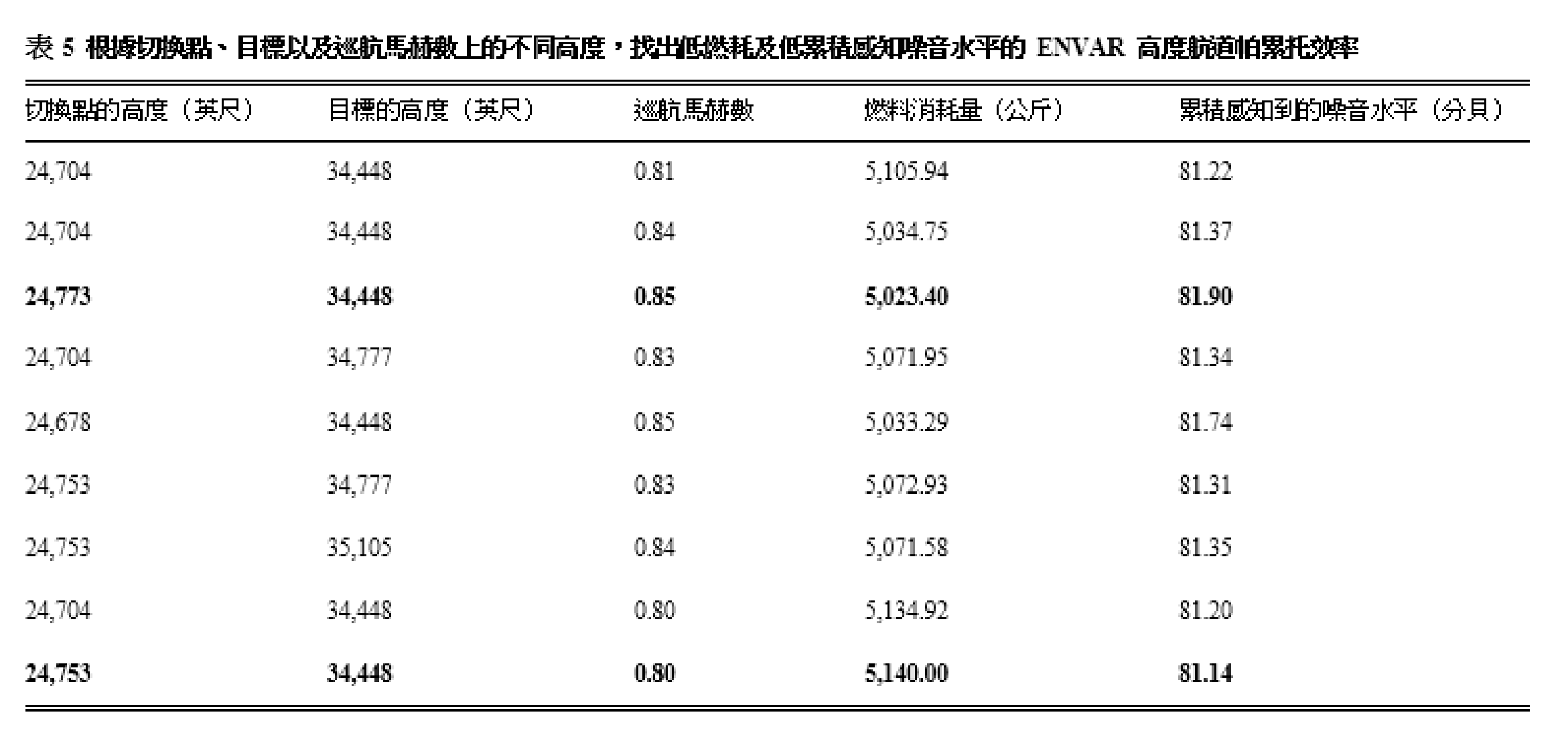
图 10 底部显示了三个离散设计变量(巡航马赫数、切换点高度及目标高度)的分布,以及其对目标函数的影响(燃料消耗及累积感知到的噪音水平)。左边首三列的横轴显示了设计变量领域,而最后两列则显示了目标函数范围。最顶两行的纵轴代表了巡航马赫数和目标高度,而最后两行则代表目标。每列顶部的图表是柱状图,沿著对角线的三个柱状图显示了设计空间产生的样本分布,最后两个柱状图则是这些样本的输出。在优化期间,除了接近上限目标高度的设计变量外,其余大部分都分布均匀。我们从第一列观察到目标位置的离散巡航马赫数和离散高度是以恒定区间产生,同时亦观察到随著切换点高度增加,燃料消耗和累积感知到的噪音水平便会降低。帕累托前沿集中在第一列图形的右边,表示最佳集合位于与较高爬升角对应的切换点高度上限附近,这亦可在图 10(顶部)的航道图中观察得到。帕累托前沿集中在第三列图形的左边,表示最佳集合位于目标高度的下限附近。我们从第四列中观察到随著燃料消耗增加,噪音水平亦会有增加倾向。表 5 列出了帕累托前沿,并以粗体字表示将燃料消耗和噪音减到最低的解决方案。我们观察到虽然两者之间的噪音水平差异甚微,但在马赫数较低(0.8)下,燃料消耗会较高,差异明显,这是因为 777-300ER 的巡航速度约为 0.84 (这是本研究所采用飞机的参照值)。表 6 列出了优化中的燃料消耗范围和累积感知噪音水平,以清晰地显示出我们制定的优化问题构思所得出的效果。表 6 中的「解决方案」列是指在优化过程中估算的所有解决方案,而帕累托前沿列则是指当中所选出的最佳集合。即使 BEKOL 解决方案的噪音范围和 ENVAR 解决方案的燃料范围很大,但帕累托前沿的燃料和噪音范围仍远低于那些解决方案。换言之,任何帕累托前沿选项,均能在未有决定优先选择的情况下得出最佳解决方案,同时无需在将燃耗和感知噪音水平减到最低之间的权衡明显的利弊。

IV. 结论
本文提出了一个优化飞行航道的方法,以在飞机离场期间沿著飞行航道降低燃料消耗及累积感知到的噪音水平。当中所采用的方法考虑了航班目的地、跑道角度、机场附近的飞机间隔、障碍物、人口密集地区以及转向情况,从而为从机场飞往强制性 ATS 位置报告点的飞机产生一组四维的离场航道,以进行 SID 规划,以及协助飞行规划人员和机师作出决策。我们所制定的策略会依次执行地平面航道规划和高度航道规划,其中前者会产生出包含初步及后续离场航道的最短航道。我们亦利用Dubins航道法来确定初步离场航道是否符合跑道角度和飞机间隔方向的限制。另外,我们亦制定了包含转向限制的考量人口因素 A* 演算法,以规划后续离场航道,从而符合与障碍物、人口密集区域及转向运动相关的限制。高度航道是透过解构飞行运动纵向控制公式而得出。我们使用 ANP 数据库以及透过评估飞行动力学而得出的性能参数,计算出航道沿途的累积感知到的噪音水平和燃料消耗量。至于高度航道的燃耗及噪音水平点的非支配集,则是利用经改良的 NSGA-II 进行离散优化,透过多目标优化得到结果。我们在从香港国际机场出发的两个飞行情境中采用了制定的方法,以针对与波音 777-300ER 相似并配备 GE90-115B 引擎的飞机来研究航道规划。包含转向限制的考量人口因素 A* 方法,透过图像比较而得出与标准仪表离场程序(SID)航道及某些实际快速存取记录器(QAR)航道非常相似的航道。多目标优化的结果显示燃料及噪音水平降低的趋势,会受到较高飞行层的切换点高度、马赫数以及强制性 ATS 位置报告点的高度所影响。此外,我们透过优化得出一小组最佳解决方案,其中的燃耗最大可减少 120 公斤,感知到的噪音变化最大可减少 0.8 分贝。这个方法可进一步用于分析飞行航道,并延伸至无人机和城市空中移动交通的航道规划,尤其是涉及与航空运输相关的复杂限制和多个决策标准。虽然我们对香港国际机场离港航班施加了符合现实的限制,但是在这项研究中,我们并未考虑空中交通的互动情况和天气条件。假如将这项研究扩展以包括这些因素,我们便能在香港国际机场四周更全面地协调和优化离场航线。透过加入相关限制,这个方法亦可以广泛地采用,从而适用于其他机场。
鸣谢
本研究工作获得香港科技大学创业补助金(项目编号: R9354)的资助,以及在研究上得到周凯旋基金会协助。作者们在此感谢国泰航空有限公司根据其与香港科技大学机械及航空航天工程系之间的数据合作协议,为本研究提供所需要的数据。此外,对于为本研究提供了实用建议的首尔地区航空办公室 Young-jong Lee 以及香港民航处 Raymond Li、为本文进行仔细核对工作的 Arjit Seth、以及为本文提供具建设性意见和实用建议的诸位匿名审阅人员,作者们亦希望表示衷心谢意。
参考资料:
- Mahashabde, A., Wolfe, P., Ashok, A., Dorbian, C., He, Q., Fan, A., Lukachko, S., Mozdzanowska, A., Wollersheim, C., Barrett, S. R., et al., "Assessing the Environmental Impacts of Aircraft Noise and Emissions," Progress in Aerospace Sciences, Vol. 47, No. 1, 2011, pp. 15–52. https://doi.org/10.1016/j.paerosci.2010.04.003
- Ho-Huu, V., Hartjes, S., Visser, H., and Curran, R., "Integrated Design and Allocation of Optimal Aircraft Departure Routes," Transportation Research Part D: Transport and Environment, Vol. 63, Aug. 2018, pp. 689–705. https://doi.org/10.1016/j.trd.2018.07.006
- Bertsch, L., and Isermann, U., "Noise Prediction Toolbox Used by the DLR Aircraft Noise Working Group," INTER-NOISE the 42nd International Congress and Exposition on Noise Control Engineering, Vol. 247, Inst. of Noise Control Engineering, Reston, VA, 2013, pp. 805–813, https://www.researchgate.net/profile/Lothar-Bertsch/publication/257773363_Noise_prediction_toolbox_used_by_the_DLR_aircraft_noise_working_group/links/00b49525d6a02d5634000000/Noise-prediction-toolbox-used-by-the-DLR-aircraft-noise-working-group.pdf
- Casalino, D., Diozzi, F., Sannino, R., and Paonessa, A., "Aircraft Noise Reduction Technologies: A Bibliographic Review," Aerospace Science and Technology, Vol. 12, No. 1, 2008, pp. 1–17. https://doi.org/10.1016/j.ast.2007.10.004
- Ho-Huu, V., Hartjes, S., Pérez-Castán, J., Visser, H., and Curran, R., "A Multilevel Optimization Approach to Route Design and Flight Allocation Taking Aircraft Sequence and Separation Constraints into Account," Transportation Research Part C: Emerging Technologies, Vol. 117, Aug. 2020, Paper 102684. https://doi.org/10.1016/j.trc.2020.102684
- Kim, D., Lyu, Y., and Liem, R. P., "Flight Profile Optimization for Noise Abatement and Fuel Efficiency During Departure and Arrival of an Aircraft," AIAA Aviation 2019 Forum, AIAA Paper 2019-3622, 2019. https://doi.org/10.2514/6.2019-3622
- Patrón, R. S. F., Botez, R. M., and Labour, D., "Vertical Profile Optimization for the Flight Management System CMA-9000 Using the Golden Section Search Method," IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Inst. of Electrical and Electronics Engineers, New York, 2012, pp. 5482–5488. https://doi.org/10.1109/IECON.2012.6389517
- "Procedure for Air Navigation Services (PANS)—Aircraft Operations," Procedure, International Civil Aviation Organization, Montreal, 2018, https://store.icao.int/en/procedures-for-air-navigation-services-pans-aircraft-operations-volume-i-flight-procedures-doc-8168
- Zachary, D. S., Gervais, J., and Leopold, U., "Multi-Impact Optimization to Reduce Aviation Noise and Emissions," Transportation Research Part D: Transport and Environment, Vol. 15, No. 2, 2010, pp. 82–93. https://doi.org/10.1016/j.trd.2009.09.005
- Prats, X., Puig, V., Quevedo, J., and Nejjari, F., "Multi-Objective Optimisation for Aircraft Departure Trajectories Minimising Noise Annoyance," Transportation Research Part C: Emerging Technologies, Vol. 18, No. 6, 2010, pp. 975–989. https://doi.org/10.1016/j.trc.2010.03.001
- Torres, R., Chaptal, J., Bès, C., and Hiriart-Urruty, J.-B., "Optimal, Environmentally Friendly Departure Procedures for Civil Aircraft," Journal of Aircraft, Vol. 48, No. 1, 2011, pp. 11–22. https://doi.org/10.2514/1.C031012
- Ho-Huu, V., Hartjes, S., Visser, H. G., and Curran, R., "An Efficient Application of the MOEA/D Algorithm for Designing Noise Abatement Departure Trajectories," Aerospace, Vol. 4, No. 4, Nov. 2017, pp. 1–15. https://doi.org/10.3390/aerospace4040054
- Filippone, A., Zhang, M., and Bojdo, N., "Validation of an Integrated Simulation Model for Aircraft Noise and Engine Emissions," Aerospace Science and Technology, Vol. 89, June 2019, pp. 370–381. https://doi.org/10.1016/j.ast.2019.04.008
- Thomas, J., and Hansman, R. J., "Evaluation of the Impact of Transport Jet Aircraft Approach and Departure Speed on Community Noise," Massachusetts Inst. of Technology, Cambridge, MA, 2020, https://rosap.ntl.bts.gov/view/dot/56957
- Chai, R., Savvaris, A., Tsourdos, A., Xia, Y., and Chai, S., "Solving Multiobjective Constrained Trajectory Optimization Problem by an Extended Evolutionary Algorithm," IEEE Transactions on Cybernetics, Vol. 50, No. 4, 2018, pp. 1630–1643. https://doi.org/10.1109/TCYB.2018.2881190
- Kant, K., and Zucker, S. W., "Toward Efficient Trajectory Planning: The Path-Velocity Decomposition," International Journal of Robotics Research, Vol. 5, No. 3, 1986, pp. 72–89. https://doi.org/10.1177/027836498600500304
- Hartjes, S., and Visser, H., "Efficient Trajectory Parameterization for Environmental Optimization of Departure Flight Paths Using a Genetic Algorithm," Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Vol. 231, No. 6, 2017, pp. 1115–1123. https://doi.org/10.1177/0954410016648980
- Zhang, Y., Zhang, R., and Li, H., "Graph-Based Path Decision Modeling for Hypersonic Vehicles with No-Fly Zone Constraints," Aerospace Science and Technology, Vol. 116, Sept. 2021, Paper 106857. https://doi.org/10.1016/j.ast.2021.106857
- Zhang, Z., Du, R., and Cowlagi, R. V., "Randomized Sampling-Based Trajectory Optimization for UAVs to Satisfy Linear Temporal Logic Specifications," Aerospace Science and Technology, Vol. 96, Jan. 2020, Paper 105591. https://doi.org/10.1016/j.ast.2019.105591
- Qian, K., Liu, Y., Tian, L., and Bao, J., "Robot Path Planning Optimization Method Based on Heuristic Multi-Directional Rapidly-Exploring Tree," Computers & Electrical Engineering, Vol. 85, July 2020, Paper 106688. https://doi.org/10.1016/j.compeleceng.2020.106688
- Li, Z., Yang, X., Sun, X., Liu, G., and Hu, C., "Improved Artificial Potential Field Based Lateral Entry Guidance for Waypoints Passage and No-Fly Zones Avoidance," Aerospace Science and Technology, Vol. 86, March 2019, pp. 119–131. https://doi.org/10.1016/j.ast.2019.01.015
- Wang, H., and Pan, W., "Research on UAV Path Planning Algorithms," IOP Conference Series: Earth and Environmental Science, Vol. 693, IOP Publ., Bristol, England, U.K., 2021, Paper 012120, https://iopscience.iop.org/article/10.1088/1755-1315/693/1/012120/pdf
- Haghighi, H., Asadi, D., and Delahaye, D., "Multi-Objective Cooperated Path Planning of Multiple UAVs Based on Revisit Time," Journal of Aerospace Information Systems, Vol. 18, No. 12, 2021, pp. 1–14. https://doi.org/10.2514/1.I010866
- Heidari, H., and Saska, M., "Collision-Free Trajectory Planning of Multi-Rotor UAVs in a Wind Condition Based on Modified Potential Field," Mechanism and Machine Theory, Vol. 156, Feb. 2021, Paper 104140. https://doi.org/10.1016/j.mechmachtheory.2020.104140
- Guo, J., Li, B., and Ji, Y., "A Control Parametrization Based Path Planning Method for the Quad-Rotor UAVs," Journal of Industrial & Management Optimization, Vol. 13, No. 5, March 2021, pp. 1079–1100. https://doi.org/10.3934/jimo.2021009
- Huang, Y., Chen, J., Wang, H., and Su, G., "A Method of 3D Path Planning for Solar-Powered UAV with Fixed Target and Solar Tracking," Aerospace Science and Technology, Vol. 92, Sept. 2019, pp. 831–838. https://doi.org/10.1016/j.ast.2019.06.027
- Abd Algfoor, Z., Sunar, M. S., and Kolivand, H., "A Comprehensive Study on Pathfinding Techniques for Robotics and Video Games," International Journal of Computer Games Technology, Vol. 2015, April 2015, Paper 736138. https://doi.org/10.1155/2015/736138
- Kavraki, L., and Latombe, J. C., "Randomized Preprocessing of Configuration Space for Path Planning: Articulated Robots," Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’94), Vol. 3, Inst. of Electrical and Electronics Engineers, New York, 1994, pp. 1764–1771. https://doi.org/10.1109/IROS.1994.407619
- Karaman, S., and Frazzoli, E., "Sampling-Based Algorithms for Opti-mal Motion Planning," International Journal of Robotics Research, Vol. 30, No. 7, 2011, pp. 846–894. https://doi.org/10.1177/0278364911406761
- Andrews, J. R., "Impedance Control as a Framework for Implementing Obstacle Avoidance in a Manipulator," Master's Thesis, Dept. of Mechanical Engineering, Massachusetts Inst. of Technology, Cambridge, MA, 1983.
- Koren, Y., and Borenstein, J., "Potential Field Methods and Their Inherent Limitations for Mobile Robot Navigation," Proceedings of 1991 IEEE International Conference on Robotics and Automation, Vol. 2, April 1991, pp. 1398–1404. https://doi.org/10.1109/ROBOT.1991.131810
- Betts, J. T., "Survey of Numerical Methods for Trajectory Optimization," Journal of Guidance, Control, and Dynamics, Vol. 21, No. 2, 1998, pp. 193–207. https://doi.org/10.2514/2.4231
- Petereit, J., Emter, T., Frey, C. W., Kopfstedt, T., and Beutel, A., "Application of Hybrid A* to an Autonomous Mobile Robot for Path Planning in Unstructured Outdoor Environments," ROBOTIK 2012; 7th German Conference on Robotics, Verband Deutscher Elektrotech-niker (VDE), May 2012, pp. 1–6, https://ieeexplore.ieee.org/document/6309512
- The Defence Mapping Agency (DMA) World Geodetic System 84 Development Committee, "Department of Defense World Geodetic System 1984: Its Definition and Relationships with Local Geodetic Systems," United States Defense Mapping Agency TR 8350.2, Sept. 1991, https://ia800106.us.archive.org/29/items/DTIC_ADA280358/DTIC_ADA280358.pdf
- "Aeronautical Information Manual," Federal Aviation Administration, 2008, https://www.faa.gov/air_traffic/publications/atpubs/aim_html/chap1_section_2.html
- McGrath, C. N., and Macdonald, M., "General Perturbation Method for Satellite Constellation Reconfiguration Using Low-Thrust Maneuvers," Journal of Guidance, Control, and Dynamics, Vol. 42, No. 8, 2019, pp. 1676–1692. https://doi.org/10.2514/1.G003739
- Dubins, L. E., "On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents," American Journal of Mathematics, Vol. 79, No. 3, 1957, pp. 497–516, https://www.jstor.org/stable/2372560
- Jha, B., Chen, Z., and Shima, T., "On Shortest Dubins Path via a Circular Boundary," Automatica, Vol. 121, Nov. 2020, Paper 109192. https://doi.org/10.1016/j.automatica.2020.109192
- Hart, P. E., Nilsson, N. J., and Raphael, B., "A Formal Basis for the Heuristic Determination of Minimum Cost Paths," IEEE Trans- actions on Systems Science and Cybernetics, Vol. 4, No. 2, 1968, pp. 100–107. https://doi.org/10.1109/TSSC.1968.300136
- Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T., "A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II," IEEE Transactions on Evolutionary Computation, Vol. 6, No. 2, 2002, pp. 182–197. https://doi.org/10.1109/4235.996017
- Mailund, T., "Divide and Conquer and Dynamic Programming," Introduction to Computational Thinking, Springer, New York, 2021, pp. 247–288. https://doi.org/10.1007/978-1-4842-7077-6_9
- Kim, D., Seth, A., and Liem, R. P., "Data-Enhanced Dynamic Flight Simulations for Flight Performance Analysis," Aerospace Science and Technology, Vol. 121, Feb. 2022, Paper 107357. https://doi.org/10.1016/j.ast.2022.107357
- "Standard Atmosphere," ISO/TC 20/SC 6, International Organization for Standardization, Geneva, 1975, https://www.iso.org/standard/7472.html
- Polhamus, E. C., A Simple Method of Estimating the Subsonic Lift and Damping in Roll of Sweptback Wings, Vol. 1862, NACA, 1949, https://ntrs.nasa.gov/citations/19930082534
- Dubs, F., "ProfIlform und Polare," Aerodynamik der reinen Unterschallströmung, Vol. 1, Springer, Berlin, 2013, pp. 167–235. https://doi.org/10.1007/978-3-0348-5295-1
- Jahanmiri, M., "Aircraft Drag Reduction: An Overview," Chalmers Univ. of Technology, Gothenburg, Sweden, 2011, https://publications.lib.chalmers.se/records/fulltext/137214.pdf
- Bouhlel, M. A., Hwang, J. T., Bartoli, N., Lafage, R., Morlier, J., and Martins, J. R. R. A., "A Python Surrogate Modeling Framework with Derivatives," Advances in Engineering Software, Vol. 135, Sept. 2019, Paper 102662. https://doi.org/10.1016/j.advengsoft.2019.03.005
- The Society of Automotive Engineers (SAE) A-21 Aircraft Noise Measure and Noise Aviation Emission Modeling Committee, "Procedure for the Calculation of Airplane Noise in the Vicinity of Airports," Society of Automotive Engineers, Aerospace Information Rept. 1845, Sept. 1995. https://doi.org/10.4271/AIR1845
- European Civil Aviation Conference (ECAC), "Report on Standard Method of Computing Noise Contours Around Civil Airports," Euro-pean Civil Aviation Conference, ECAC.CEAC Doc 29, 2016, https://www.ecac-ceac.org/images/documents/ECAC-Doc_29_4th_edition_Dec_2016_Volume_1.pdf
- Boeker, E. R., Dinges, E., He, B., Fleming, G., Roof, C. J., Gerbi, P. J., Rapoza, A. S., Hermann, J., et al., "Integrated Noise Model (INM) Version 7.0 Technical Manual," United States Federal Aviation Administration Office of Environment and Energy, 2008, https://www.faa.gov/about/office_org/headquarters_offices/apl/research/models/inm_model/inm7_0c/media/INM_7.0_Technical_Manual.pdf
注:
‡ https://www.ais.gov.hk
¶ https://www.ais.gov.hk
§ https://earth.google.com
** www.cad.gov.hk/english/ac_path.html
†† https://sedac.ciesin.columbia.edu/data/set/gpw-v4-admin-unit-center-points-population-estimates-rev11/data-download
‡‡ https://www.aircraftnoisemodel.org/
作者:
香港科技大学机械及航空航天工程系助理教授Rhea Liem教授
香港科技大学博士后研究员Dajung Kim博士
副主编:
I Hwang
2023年3月

