使用宇宙標準計時器測量宇宙


自人類於地球誕生，我們一直嘗試了解我們所在的宇宙。經過了數千載的觀察和思考，我們已經發展了一套宇宙學標準模型，可讓我們更好地描述宇宙熱大爆炸以來的演化。然而，隨著科技進步和精確測量技術的發展，更多結果顯示觀測和理論之間存在著矛盾，其中哈勃常數疑難，便是現代宇宙學中的一個迫在眉睫、亟待解決的問題。

解決問題，必先了解問題。為化解上述宇宙學危機，科學家提出了多種方法，包括修正基礎物理學和觀測上的系統偏差。另一邊廂，我們也為測量宇宙提出了一個名為「宇宙標準計時器」的新方法。採用此方法來研究宇宙動力學系統的演化，可讓我們了解宇宙在不同時期的狀態。掌握更多宇宙演化的信息，將助我們更好地理解宇宙學模型。

宇宙的演化

現代宇宙學始自於將引力描述為時空幾何廣義相對論。1917年，阿爾伯特·愛因斯坦（Albert Einstein）以廣義相對論為基礎，建立了他的宇宙學模型[1]，並據此描述了一個靜態的宇宙。然而在宇宙擾動之下，這個靜態宇宙學模型是不穩定的。在二十世紀二十年代，亞歷山大·弗裡德曼（Alexander Friedmann）提出了廣義相對論的宇宙學解[2, 3]，認為視乎物質密度和時空曲率，宇宙既可能是膨脹的，也可能是收縮的。與此同時，喬治·勒梅特（Georges Lemaître）獨立提出了相對論化的宇宙學方程，並指出可能是一個原初原子的爆炸引致宇宙誕生[4]。

直到1929年，宇宙演化的問題才首次獲得解答。埃德溫·哈勃（Edwin Hubble）發現遙遠星系的光譜發生紅移 [5]，這意味著這些星系正在遠離我們，而且遠離的速度與它們和地球的距離成正比，這就是著名的哈勃定律（見圖1）。


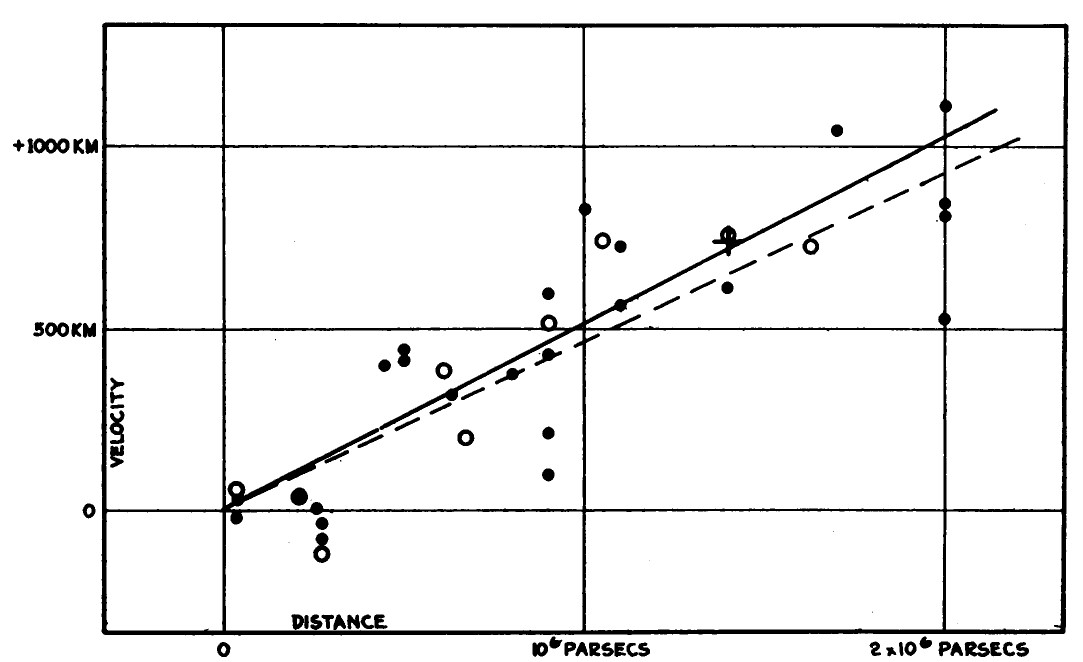
圖1: 銀河外星雲的速度與距離關係[5]

所以，哈勃的觀測證明了我們的宇宙正在膨脹。為了描述宇宙的膨脹速度，量化宇宙膨脹，我們把星系速度與距離關係的斜率定義為哈勃參數或稱之為哈勃常數。

喬治·伽莫夫（ George Gamow ）通過研究相對論宇宙學理論和哈勃的觀測所得，提出宇宙在最初始之時處於很熱並且高密度的狀態，但隨著宇宙的膨脹，初始的等離子態慢慢的冷卻並且形成了最初的元素[6, 7]。但是這一對宇宙的描述並沒有被其他的物理學家接受。提出穩態宇宙學模型的物理學家弗雷德·霍伊爾（Fred Hoyle）在一個BBC的訪談中，戲稱伽莫夫的理論為「大爆炸」。

之後的十幾年，熱大爆炸理論和穩態理論之間的爭論曠日持久。直到1965年，射電天文學家阿諾·彭齊亞斯（Arno Penzias）和羅伯特·威爾遜（(Robert Wilson）發現在空中存著一個均勻的微波波段背景噪聲，其後被證明是宇宙微波背景[8]（見圖2）。


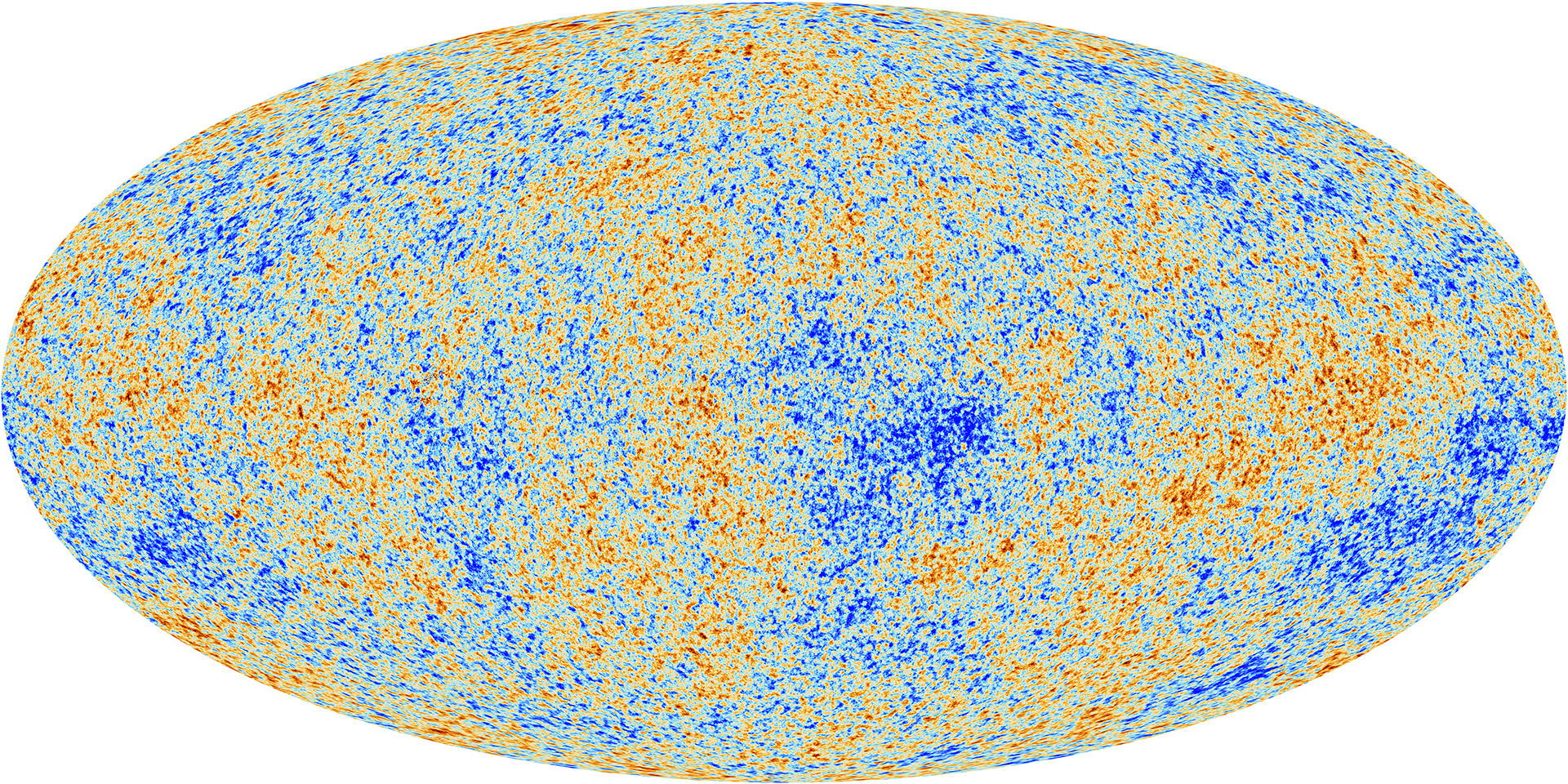
圖2: Planck 衛星測量的宇宙微波背景[9]

由於宇宙微波背景可以在宇宙早期的初始高溫高密度狀態的冷卻過程中自然形成，宇宙微波背景的存在證明了熱大爆炸理論成立，熱大爆炸模型亦因而變成了宇宙學標準模型的基礎。

過去幾十年，隨著精確宇宙學的不斷發展，一些重要的宇宙學現象亦陸續被發現，包括除了我們已知的宇宙外還存在著一個黑暗宇宙。1970年，薇拉·魯賓（Vera Rubin），肯特·福特（Kent Ford）和肯·弗裡曼（Ken Freeman）測量了銀河系的旋轉曲線，但測量結果與他們所預期的表現並不相符[10, 11]。根據觀測結果，科學家提出了一個宇宙存在一種特殊物質的假說，這種物質只參與引力相互作用，並不發光，因此也被稱為「暗物質」。1998年，科學家在研究地球附近Ia類超新星時發現，宇宙的膨脹正在加速[12]，故此應有一種特殊能量產生排斥力來加速宇宙的膨脹，而這種能量被稱為「暗能量」。為了知道這些不同的成分在宇宙中的所佔比例，2009年，普朗克衛星發射升空探測宇宙微波背景的各向異性，最終結果於2018年發表[13]。結果顯示，目前我們已知的物質只佔宇宙總能量的5%，暗物質佔26.5%，暗能量佔68.5%。

現在我們已經建立了宇宙學標準模型（或稱Lambda冷暗物質模型，Lambda指暗能量）。根據這個模型，宇宙的演化取決於其不同的成分，其中物質（包括正常物質和暗物質）引起的吸引力會減低宇宙的膨脹速度，而暗能量所產生的排斥力則會加快宇宙的膨脹。宇宙的總能量密度決定了宇宙的膨脹速度，或者哈勃參數。如果我們知道物質和暗能量演化的動力學，或許我們就可以精確地測量哈勃參數，進而更好地了解宇宙的過去和未來。

測量宇宙

欲研究宇宙的演化，先須測量宇宙，而測量的第一步，就是量丈宇宙的距離。然而這項工作殊不簡單，要懂得以由小見大，知微見著。方法之一是應用三角學，一個等腰三角形如果已知底長和頂角角度，求其腰長，那麼以底長除以頂角角度就可得出其大約長度。在我們的太陽系中就存在著這麼一個等腰三角形。如果我們看著天空中的一顆恒星，我們可以測量這顆恒星相對於我們的視角。而由於地球環繞太陽公轉，這顆恒星的視角也在不斷變化。經過半年的公轉，地球已在太陽系中移動了兩個天文單位，這有效地改變了這顆恒星相對於我們的視角（見圖3）。


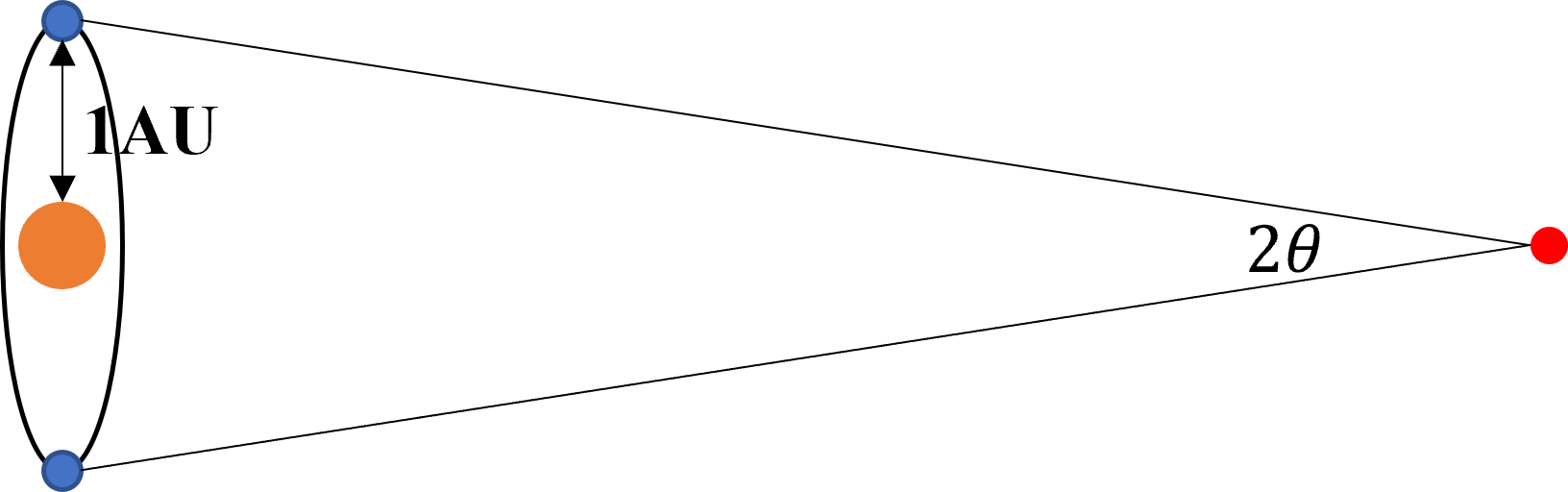
圖3: 通過恒星的視差來測量距離

通過測量恒星視角的變化，我們可以求得恒星與地球的距離。如果說視角的變化是1弧秒，那麼測量到的距離就是1秒差距，即等於3.26光年。秒差距這個單位也常用於描述宇宙學距離。這種基於恒星視角測量距離的方法被稱之為視差法，它可以用來測量大致幾千秒差距的距離。然而由於角度測量的精度限制，更遠的距離就難以通過視差法測量。

不過，若要測量更長的宇宙學距離，那就不是一個純粹的幾何學問題了。因為我們的宇宙是處在一個膨脹而不是靜止的狀態。當接收到遙遠的宇宙學信號時，這個信號已經在空間傳播了一段很長的時間。換言之，這信號被發出時，當時宇宙和我們現在的宇宙並不一樣。所以，測量宇宙學距離也牽涉及宇宙是如何演化的問題。因此在這樣的測量中，被觀測的量應包含宇宙在信號發出時的狀態和在信號傳播過程中的動力學演化。

在描述宇宙狀態的時候，我們通常使用標度因子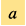，它是過去宇宙和現在宇宙的尺度比例。然而標度因子不能直接用來觀測，我們需要使用其他的可觀測量來描述宇宙的尺度。當我們考慮一個宇宙學信號，例如一個來自遙遠恒星的光子，在它從信號源傳播到地球的過程中，宇宙膨脹將會拉長光子的波長，這會導致觀測光譜紅移，而我們可以使用信號譜中觀測到的宇宙學紅移來得到宇宙的標度因子。就宇宙學距離測量而言，我們需要通過觀測特定物體來構建測量方法。這個特定的觀測物體應有一個標準屬性用做距離校準。目前我們已經發展了多種測量宇宙學距離的方法，例如標準燭光、標準尺子，以及標準汽笛，這都是讓我們理解宇宙尺度物理的工具。

假設我們有一些亮度相同的蠟燭，如果從我們本身的位置開始，把這些蠟燭放在不同的位置，那麼蠟燭距離我們越遠，燭光看來就越黯淡。這是由於燭光的絕對亮度是固定的，而燭光的視亮度是蠟燭與我們之間距離的平方反比。所以通過比較標準燭光的視亮度和絕對亮度，就可以測算出它與我們的距離，這種方法被稱之為標準燭光法（見圖4）。


圖4: 通過標準燭光和標準尺子測量宇宙（圖片來源: NASA）

在宇宙中，具有標準絕對亮度的可觀測物體都可以作為標準燭光的候選者。1908年，亨麗愛塔·斯萬·勒維特（Henrietta Swan Leavitt）發現在造父變星的亮度和脈動週期中存在很強烈的直接關聯[14, 15]（見圖5）。


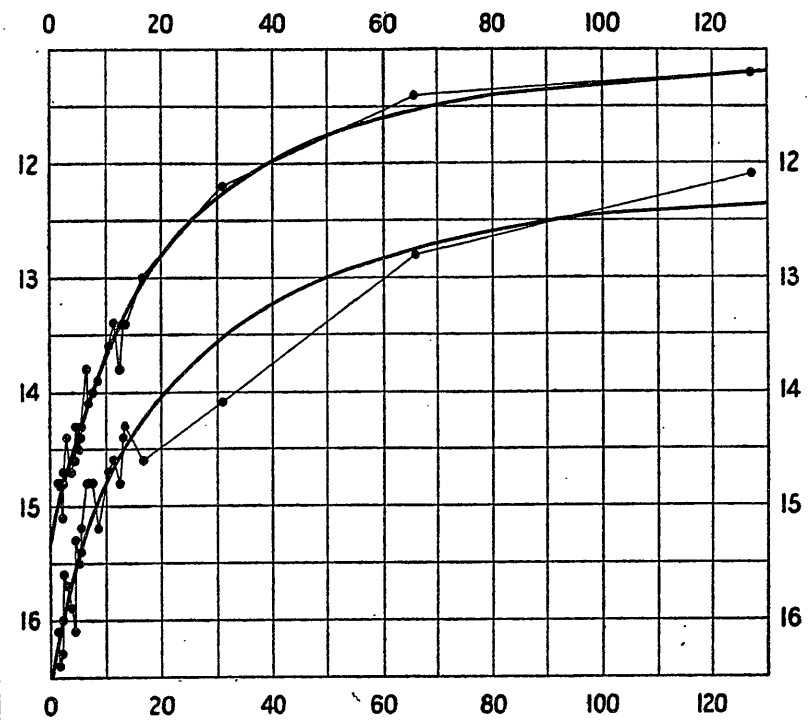
圖5: 造父變星的亮度與脈動週期的關係[15]

二十世紀三十年代，沃爾特·巴德（Walter Baade）和弗裡茨·茲威基（Zwicky Fritz）發現超新星[16]，超新星其後被證明具有固定峰值的亮度。通過比較這些標準燭光的視亮度和絕對亮度，我們可以得出它們的亮度距離，這是一個描述光子的能量密度從源頭傳播到我們所在位置過程中如何演化的一個物理量。通過其信號光譜，我們也可以獲得它們的紅移值，這為我們提供了宇宙在信號被發射時的尺度。通過亮度距離和紅移的關係，宇宙從過去到現在的演化過程也被限制住了。有了標準燭光的幫助，我們就可以測量出高達幾億秒差距的宇宙距離。

對於更遠距離的測量，我們需要動用其他的方法。假設我們有一些相同長度的尺子，如果從我們本身的位置開始，把這些尺子放在不同的地方，那麼距離我們越遠的尺子看起來就會越小。這是因為尺子的絕對長度是固定，而觀測到的角間距是距離的反比。所以通過比較觀測到的角間距和它們的絕對長度，就可得出尺子和我們的距離(見圖4)。在宇宙中，一旦知道物體的標準尺度，該物體就可以選作為標準尺子。星系的分佈中存在著這樣的尺度，稱為重子聲學振盪尺度。在宇宙微波背景形成前，宇宙處於熱等離子態。那時候，宇宙中的暗物質隨機分佈，對重子物質產生強大的吸引力。然而，熱等離子體中的光子卻對重子物質產生強大的排斥力，並且引起重子物質的振盪。宇宙不斷膨脹，溫度也隨之慢慢下降，光子開始從重子物質的相互作用中退耦，形成宇宙微波背景。這時候，那把特殊的尺度留在了重子物質的分佈中，其後留在了星系的分佈中，那就是前文提到的重子聲學振盪尺度。通過觀測星系之間的角間距和它們的紅移，我們能掌握橫向共動距離和紅移的關係，進而幫助我們限制宇宙的演化到達數十億秒的差距。

當探測到第一個引力波事件後[17]，測量宇宙又有了一種名為標準汽笛法的新方法。被探測到的引力波由一個雙黑洞合併發出，其振幅取決於雙黑洞的紅移質量和從黑洞到我們的亮度距離。通過引力波的相位，我們可以取得黑洞的紅移質量，繼而得出雙黑洞的亮度距離（見圖6）。


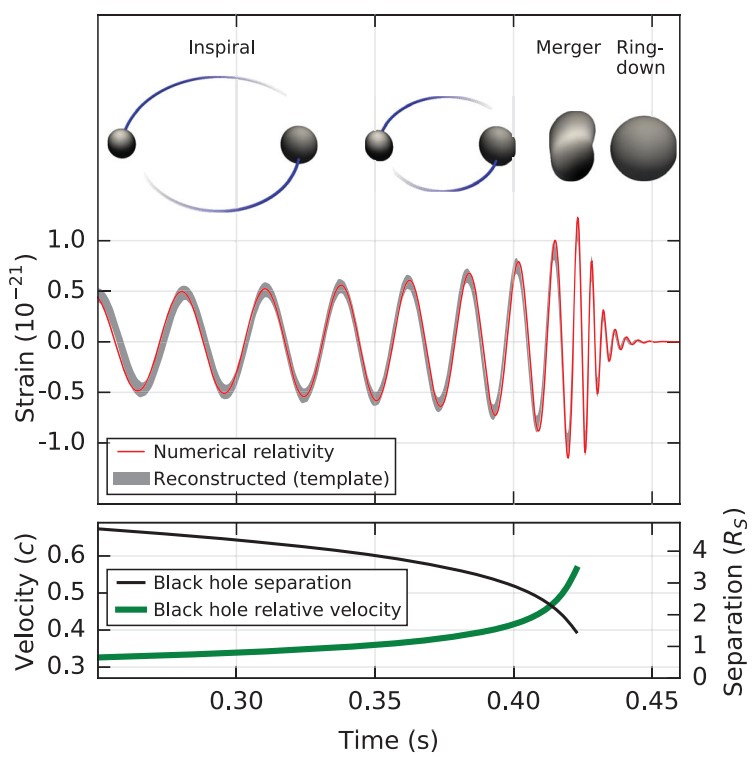
圖6: 第一個觀測到的引力波事件GW150914 [17]

但是，為了限制宇宙的演化，我們仍需獲得引力波源的紅移，但這並不能直接從引力波中提取。2017年，科學家觀測一例雙中子星合併事件[18]。合併過程不僅輻射出引力波，也輻射出電磁波，讓我們既可以從引力波中提取亮度距離的信息，也可以從電磁波中提取宇宙紅移的信息，而亮度距離和紅移的關係又能幫助我們限制宇宙學模型。隨著引力波探測器的發展更代升級，標準汽笛法可以測量的距離尺度高達數十億秒差距。

除了上述方法，我們也可以通過宇宙微波背景進行一些關於早期宇宙的測量，例如根據Lambda冷暗物質模型擬合宇宙微波背景的功率譜（見圖7），從而估算宇宙學參數 [13]。


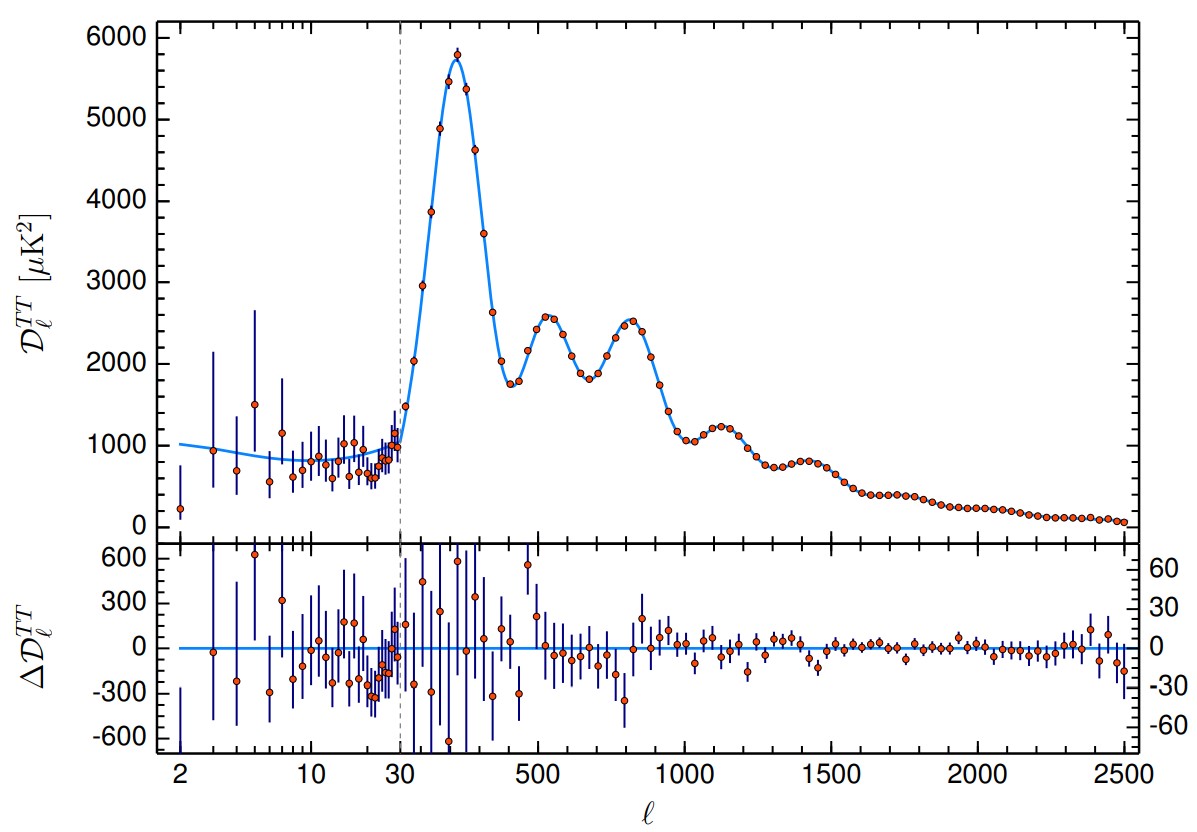
圖7: Planck 2018宇宙微波背景輻射溫度功率譜 [13]

宇宙學危機

在研究宇宙演化的過程中，哈勃參數的數值至關重要，參數的數值代表著宇宙的膨脹速度。當哈勃發現宇宙正在膨脹後，他先測量了哈勃參數，得出500km/s/Mpc這個約數（見圖1中的斜率），這代表距離我們一百萬秒差距的星系正在以500km/s的速度遠離我們。隨後的幾十年觀測技術不斷提升，哈勃參數的測量值已經從500km/s/Mpc降到了大約70km/s/Mpc。測量哈勃參數標準燭光或者低紅移標準尺子等多種方法，而且都可以用來測量晚期宇宙的膨脹速度。此外，也可以通過擬合宇宙微波背景的功率譜和高紅移重子聲學振盪取得哈勃參數，用來測量早期宇宙。不過近年來，科學家發現哈勃參數的測量並不一致[19]，晚期宇宙的測量得出的哈勃參數為73.0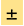1.0 km/s/Mpc，而早期宇宙的測量則為67.4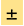0.5 km/s/Mpc（見圖8）。


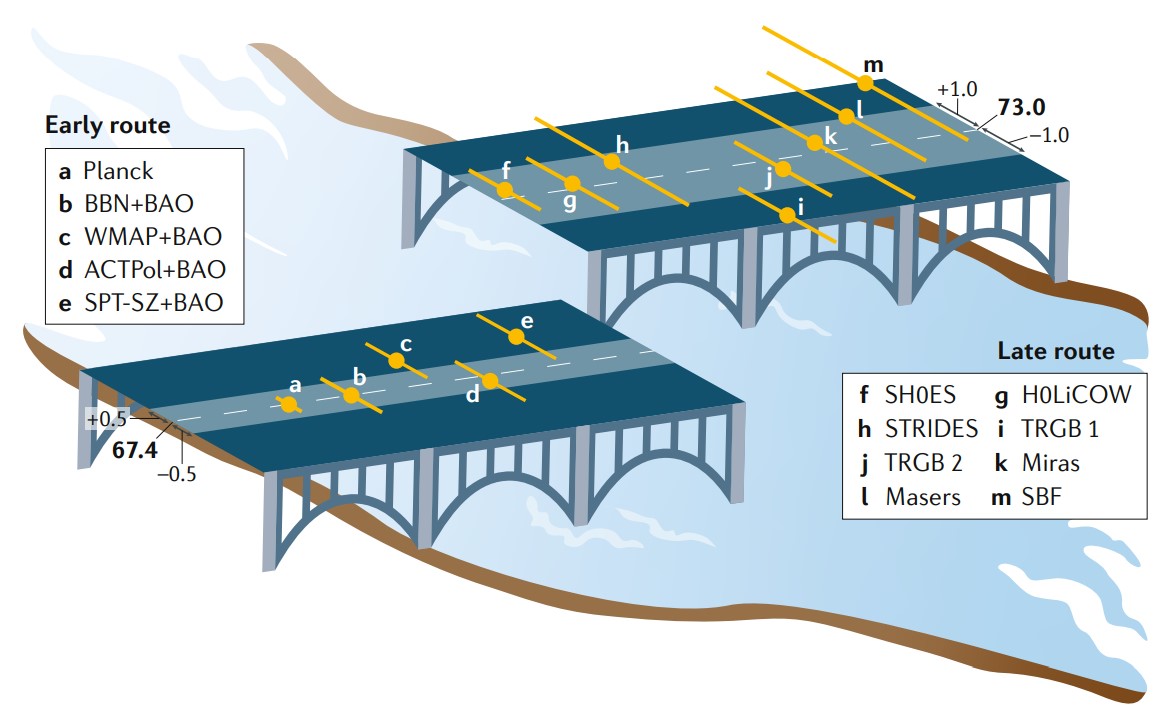
圖8: 哈勃參數在早期宇宙和晚期宇宙的測量值[19]

雖然哈勃參數通過早期和晚期宇宙途徑測出的結果兩者之差相對於自身值來說不大，但是測量的精度相對於測量上的偏差則算高。統計學上來說，哈勃參數的測量差距達到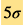 的置信度，意味著這種偏差是由測量誤差導致的可能性大約是2.9×10−7。由於這種可能性太小，故應該是因為存在著某些機制而導致哈勃參數出現了這一偏差。這個問題成為現代宇宙學的危機，稱為哈勃常數疑難。

除了哈勃常數疑難，現代宇宙學中也有其他問題有待解決[20]，例如不同物質密度測量不一致，不同的宇宙學極化測量不一致。這些問題促使我們研發更好的宇宙學模型，並探索隱藏在宇宙演化背後的基礎物理。

宇宙標準計時器：一種測量宇宙的新方法

為了理解藏身在宇宙學危機背後的物理，我們得構建一種新的宇宙測量法，來追蹤宇宙早期至今的演化。只有透過深入理解宇宙的演化歷史，才能建立一個更好的宇宙學模型。

在上述關於測量方法的討論中，宇宙的演化受距離和紅移的關係所限制。紅移為我們提供了宇宙在信號發出時的尺度，距離則提供了宇宙從信號發出至今的演化信息。雖然從了解尺度因子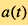的演化入手是更直接的研究宇宙演化的方法，但由於尺度因子不能被直接觀測得到，科學家便以研究宇宙紅移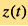的演化來作為替代。尺度因子和宇宙紅移的關係為.

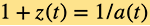宇宙中存在著許多動力學系統，各自按其內在機制而演化。經過一段長時間的演化，這些系統的狀態已起了實質的變化。通過研究其演化的內在機制，我們可以獲得系統從初始狀態演化至後期狀態的物理演化時間。由於這些動力學系統的演化是獨立於宇宙演化的，因此它們的物理演化時間可視作為一個獨立的宇宙時間測量。這些動力學系統在演化時，會釋放一些宇宙學信號，例如電磁波和引力波。而在這些信號發出至傳遞到我們的過程中，宇宙膨脹將其波長伸拉，同時在信號譜中留下宇宙紅移。所以，當我們觀測到某個特定的動力學系統的宇宙信號時，便可以從信號中提取宇宙紅移，並通過比較動力學系統的初始態和觀測狀態，得出它們的物理演化時間。據此，我們可以構建一個紅移時間關係，這也告訴了我們宇宙紅移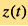是如何演化的。在上述的機制中，動力學系統就像是宇宙中的一個標準計時器一樣工作，告訴我們宇宙在不同時刻的物理狀態。

以上就是標準計時器的基本構思。為構建一個實用的標準計時器，研究宇宙從早期到晚期的演化，我們需要選擇一個特定的動力學系統，而這個系統應該從宇宙早期一直存在至今。不過，常見的天體，例如恒星和天體物理黑洞，只存在於晚期宇宙。故此，構建標準計時器就得採用一種特殊的黑洞，就是原初黑洞。

恒星死亡後，引力坍縮形成黑洞，稱為天體物理黑洞。由於恒星只存在於晚期宇宙，天體物理黑洞也只能存在於晚期宇宙。天體物理黑洞的質量一般大於太陽質量的三倍，所產生的引力足以凌駕基本粒子間的排斥作用力。但是原初黑洞不同，被斯蒂芬·霍金（Stephen Hawking）和伯納德·卡爾（Bernard Carr）於1974年率先提出原初黑洞[21]，指它由原初擾動的引力坍縮所形成，故此是從早期宇宙一直存在至今的天體。由於在早期宇宙沒有足夠的排斥作用力，原初黑洞的質量可以是大於10-5克的任何值[21]。

選定原初黑洞來構建標準計時器後，原初黑洞發出的宇宙學信號便成為重要的分析元素。但是，黑洞會發出信號這點說來有點奇怪，因為在我們的觀念中，黑洞是漆黑的而且有著可怕的吸引力，甚至連光都逃脫不了。要是這樣的話，宇宙信號又是如何逃離黑洞傳到地球呢?事實上，黑洞其實不是黑的。1974年，霍金發表研究，指即使是黑洞也能發出輻射和粒子[22, 23]，這就是著名的霍金輻射。換言之，黑洞也能發出信號，只是黑洞質量的平方反比，功率非常微弱。一般來說，天體物理黑洞的質量大於太陽質量的三倍，黑洞發出的霍金輻射非常微弱，以至於我們時至今天都沒有觀測得到。然而，原初黑洞改變了這個看法。由於原初黑洞的質量可以非常小，所發出的霍金輻射的功率強到足以被觀測到。除了霍金輻射，黑洞產生的引力效應也可被視作一種重要的宇宙學信號，尤其是源自雙黑洞系統的引力波。如果雙黑洞的質量足夠大，輻射出的引力波也是可以被觀測到的。

我們研究的第一個動力學系統是小質量原初黑洞群[24]。這個動力學系統具有標準的初始狀態，即原初黑洞的初始質量函數。由於原初黑洞形成於相同的原初擾動的引力坍縮，故每個原初黑洞群的初始質量函數都應該是一樣的。隨著原初黑洞發出霍金輻射，其質量慢慢降低。此外，相對於更重的原初黑洞，小質量原初黑洞的質量損失更大。這種質量損失會改變原初黑洞的質量函數，通過研究質量函數從初始到後期的演化，我們從中就可以提取它們的物理演化時間。霍金輻射從原初黑洞群傳遞到我們的過程中，宇宙膨脹將輻射的能量密度稀釋並且伸拉其波長，導致觀測到的霍金輻射振幅比較小，而出現紅移。儘管霍金輻射譜的振幅比較小，但是原初黑洞群有著大量的原初黑洞，因此發出的霍金輻射依然可被觀測得到。通過比較紅移後的霍金輻射和標準霍金輻射譜提取出的宇宙學紅移，我們就能知道在特定物理時刻的宇宙紅移。在觀測了大量的原初黑洞群之後，我們就可以獲取紅移和時間的關係並用來限制宇宙的演化（示例見圖9）。


圖9: 通過小質量原初黑洞群構建的標準計時器

我們研究的第二種動力學系統是原初黑洞雙星系統[25]。在這樣的動力學系統中，標準的初始狀態是關於雙星系統主軸和離心率的初始概率分佈。隨著原初黑洞在雙星系統中的運動，它們的引力效應造成了時空的擾動，從而產生了引力波。發出的引力波從原初黑洞雙星中帶走了能量，這改變了雙星系統的主軸和離心率。這樣的一種機制也改變了它們關於主軸和離心率的概率分佈。所以通過研究概率分佈的演化，我們可以提取出從初始狀態到後期狀態的物理演化時間。在引力波從原初黑洞雙星傳遞到我們的過程中，宇宙膨脹伸拉了引力波的波長，並且在觀測到的引力波中留下了宇宙紅移。在引力波中的紅移也導致了觀測到的概率分佈的坐標移動。所以通過比較觀測到的概率分佈和初始的標準概率分佈，我們就可以獲得宇宙紅移。而宇宙紅移和物理演化時間的關係也因此被標定。在觀測到大量的來自原初黑洞雙星的引力波後，從早期宇宙到現在的不同物理時刻的宇宙紅移都將被標定，這也進一步告訴我們宇宙紅移和標度因子是如何演化的（示例見圖10）。


圖10: 通過原初黑洞雙星構建的標準計時器

在上述的討論中，我們主要在原初黑洞系統中構建標準計時器。事實上，宇宙中有許多動力學系統可作為標準計時器的候選者。如果一個宇宙動力學系統具備初始狀態，並且有著確切的演化機制，那麼動力學系統中的物理演化時間就可以視為宇宙時間的獨立測量。與此同時，宇宙膨脹也將宇宙紅移留在了可觀測量中。通過研究此類宇宙動力學系統，就可以獲得宇宙紅移和物理時間的關係，就像在宇宙中工作的標準計時器一樣。例如第一代恒星，如果我們知道它們的初始質量函數和恒星形成率，通過研究它們的數量演化，我們可以構建出一種新的晚期宇宙測量標準計時器。

有著標準燭光、標準尺子、標準汽笛和標準計時器這些測量技術的幫助，宇宙的奧秘將會被揭開，而人類作為一個整體也終將理解我們所生活的這個宇宙。

參考資料︰


  1. Einstein, Albert. "Cosmological considerations on the general theory of relativity." Sitzungsber.Preuss.Akad.Wiss.Berlin (Math.Phys.),(1917): 142-152.
  2. Friedmann, Alexander. "Über die krümmung des raumes." Zeitschrift für Physik 10.1 (1922): 377-386.
  3. Friedmann, Alexander. "Über die Möglichkeiteiner Welt mitkonstanternegativerKrümmung des Raumes." Zeitschrift für Physik 21.1 (1924): 326-332.
  4. Lemaître, Georges. "Un Univershomogène de masse constante et de rayon croissant rendantcompte de la vitesse radiale des nébuleuses extra-galactiques." Annales de la Société scientifique de Bruxelles. Vol. 47. 1927.
  5. Hubble, Edwin. "A relation between distance and radial velocity among extra-galactic nebulae." Proceedings of the national academy of sciences 15.3 (1929): 168-173. [6]. Gamow, George. "Expanding universe and the origin of elements." Physical review 70.7-8 (1946): 572.
  6. Alpher, Ralph A., Hans Bethe, and George Gamow. "The origin of chemical elements." Physical Review 73.7 (1948): 803.
  7. Penzias, Arno A., and Robert Woodrow Wilson. "A measurement of excess antenna temperature at 4080 Mc/s." The Astrophysical Journal 142 (1965): 419-421.
  8. Akrami, Yashar, et al. "Planck 2018 results-IV. Diffuse component separation." Astronomy & Astrophysics 641 (2020): A4.
  9. Freeman, Kenneth C. "On the disks of spiral and S0 galaxies." The Astrophysical Journal 160 (1970): 811.
  10. Rubin, Vera C., and W. Kent Ford Jr. "Rotation of the Andromeda nebula from a spectroscopic survey of emission regions." The Astrophysical Journal 159 (1970): 379.
  11. Riess, Adam G., et al. "Observational evidence from supernovae for an accelerating universe and a cosmological constant." The Astronomical Journal 116.3 (1998): 1009.
  12. Aghanim, Nabila, et al. "Planck 2018 results-VI. Cosmological parameters." Astronomy & Astrophysics 641 (2020): A6.
  13. Leavitt, Henrietta S. "1777 variables in the Magellanic Clouds." Annals of Harvard College Observatory 60 (1908): 87-108.
  14. Leavitt, Henrietta S., and Edward C. Pickering. "Periods of 25 Variable Stars in the Small Magellanic Cloud." Harvard College Observatory Circular 173 (1912): 1-3.
  15. Baade, Walter, and Fritz Zwicky. "On super-novae." Proceedings of the National Academy of Sciences 20.5 (1934): 254-259.
  16. Abbott, Benjamin P., et al. "Observation of gravitational waves from a binary black hole merger." Physical review letters 116.6 (2016): 061102.
  17. Abbott, B. P., et al. "Multi-messenger Observations of a Binary Neutron Star Merger." The Astrophysical Journal 848.2 (2017).
  18. Riess, Adam G. "The expansion of the Universe is faster than expected." Nature Reviews Physics 2.1 (2020): 10-12.
  19. Abdalla, Elcio, et al. "Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies." Journal of High Energy Astrophysics (2022).
  20. Carr, Bernard J., and Stephen W. Hawking. "Black holes in the early Universe." Monthly Notices of the Royal Astronomical Society 168.2 (1974): 399-415.
  21. Hawking, Stephen W. "Black hole explosions?." Nature 248.5443 (1974): 30-31.
  22. Hawking, Stephen W. "Particle creation by black holes." Euclidean quantum gravity. 1975. 167-188.
  23. Cai, Yi-Fu, et al. "Cosmological Standard Timers from Unstable Primordial Relics."arXiv:2112.10422 (2021).
  24. Ding, Qianhang. "Cosmological Standard Timers from Primordial Black Hole Binaries." arXiv:2206.03142 (2022).

作者︰
香港科技大學物理系博士候選人丁乾航先生
2023年1月