Measure the Universe with Cosmological Standard Timers


Since the first humans were born on Earth, we have been trying to learn about the Universe in which we inhibit. Thousands of years of observations and thinking have enabled us to develop a standard cosmological model capable of better describing the evolution of the Universe since the hot big bang. With technical progress and the development of precise measurement techniques, more results show that there is inconsistency between observation and theory, such as Hubble tension, which poses a pressing problem in modern cosmology.

Problem solving begins with understanding the problem. To solve the aforementioned cosmological crisis, a number of methods have been proposed, including modified fundamental physics and observational systematical uncertainty. Cosmological standard timers, a novel way to measure the Universe telling us the state of the Universe at different epochs by studying the evolution of cosmological dynamical systems, has also been developed. With more information about the evolution of the Universe, we are now able to have a better understanding of the cosmological model.

Evolution of the Universe

Modern cosmology starts from general relativity, which describes gravity as a geometric property of spacetime. Based on general relativity, Albert Einstein built his cosmological model [1] in 1917, which describes a static Universe. However, this static cosmological model is unstable under the cosmological perturbations. In 1920s, Alexander Friedmann solved the cosmological solution of general relativity [2, 3], which shows the Universe may be expanding or contracting depends on the matter density and curvature of the spacetime. Meanwhile, Georges Lemaître independently developed relativistic cosmological equations and pointed out that the Universe may be born from the explosion of a primordial atom [4].

Until 1929, the question about evolution of the Universe was first answered. Edwin Hubble discovered the light spectrum of distant galaxies is redshifted [5], which means these galaxies are moving away from us at speeds proportional to the distance between the galaxies and Earth (i.e. the famous Hubble's law) as shown in Fig 1.


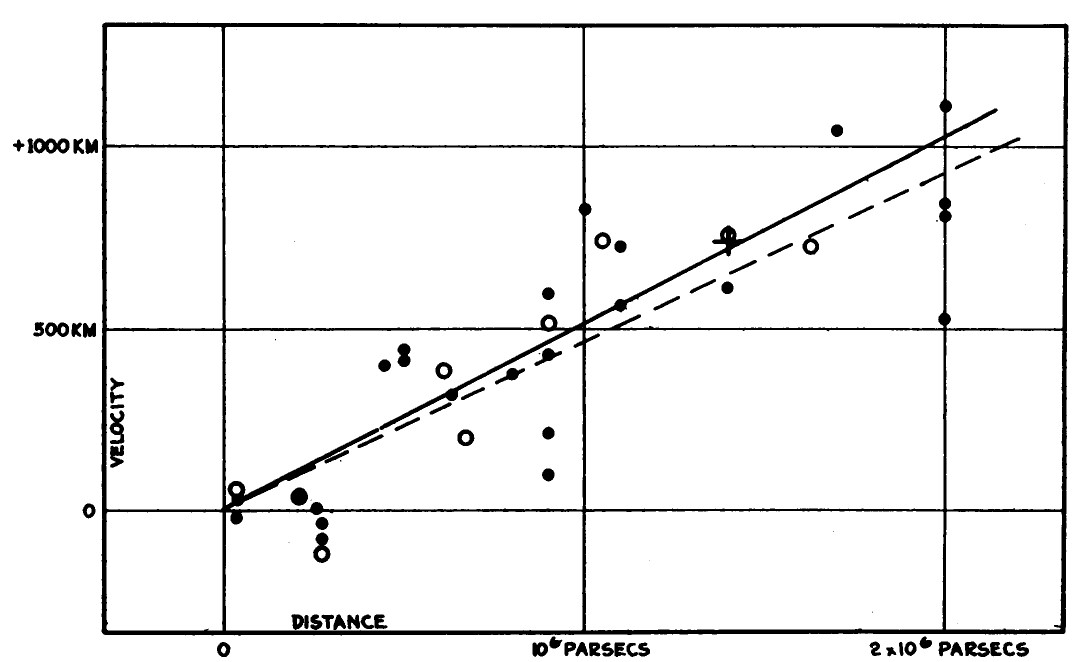
Fig 1: Velocity-distance relation among extra-galactic nebulae [5]

Therefore, Hubble's observation proves our Universe is expanding. In order to describe the expanding velocity of the Universe, we define the slope of galaxy velocity-distance relation as Hubble parameter (or Hubble Constant) to quantify the expansion of the Universe.

Based on theoretical studies about the relativistic cosmology and Hubble's observation, George Gamow proposed that the Universe is in a hot and dense state initially, and with the expansion of the Universe, the initial plasma is cooling down and forms the initial elements [6, 7]. However, such a cosmological theory that the Universe has a beginning was not accepted by other physicists. Fred Hoyle who proposed the steady state cosmological model, made fun of the Gamow's theory by calling it as a "big bang" on a BBC radio broadcast.

In the following decade, there is a prolonged debate between the hot big bang theory and the steady state theory. In 1965, radio astronomers Arno Penzias and Robert Wilson detected that there is a uniform background microwave noise in the sky, which is later found to be cosmic microwave background (CMB) [8] as shown in Fig 2.


Fig 2: The cosmic microwave background from Planck satellites [9]

The existence of the CMB proves the hot big bang theory is correct, because CMB can be naturally produced from the cooling of initial hot and dense state at the early Universe. Therefore, the hot big bang model has become the foundation of the standard cosmological model.

With the development of precision cosmology over past decades, some important cosmological phenomena have been found, including the existence of a dark Universe apart from the known Universe. In 1970, Vera Rubin, Kent Ford and Ken Freeman measured the galaxy rotation curve, which does not show the behaviour as their expectation [10, 11]. According to their observation, a hypothesis about the existence of a kind of special matter was proposed and that this kind of matter only involves in the gravitational interaction and does not emit light, therefore it is called dark matter. In 1998, a study about the nearby Type Ia supernovae showed that the expansion of the Universe is accelerating [12]. Therefore, there should exist a repulsive force to accelerate the Universe, and such repulsive force is thought to come from a kind of special energy, called dark energy. To know the percentage of different components in the Universe, Planck satellites was launched to measure the anisotropy of CMB in 2009, and the final result was published in 2018 [13]. It shows that, at present, matter known to us only occupies 5 percent of the total energy in the Universe, dark matter and dark energy occupy 26.5 percent and 68.5 percent of the total energy in the Universe respectively.

At the present, we have built the standard cosmological model or Lambda cold dark matter model (Lambda represents dark energy). In this model, the evolution of the Universe is controlled by its components, the attracted force induced by the matter (including the normal matter and dark matter) would decelerate the expansion of the Universe and the repulsive force induced by the dark energy would accelerate the expansion of the Universe. The total energy density inside the Universe determines the expanding velocity of the Universe, in other words, Hubble parameter. If we could comprehend the dynamics of matter and dark energy, or measure the Hubble parameter with high precision, we would vastly advance our knowledge on the evolution of the Universe from the past to the future.

Measure the Universe

To study the evolution of the Universe, we need to measure the Universe. To conduct such a measurement, the first thing is to know how to measure the distance in the Universe. However, measuring the cosmological distance is not easy. We have to try it from the small-scale distance. The first method comes from trigonometry, if we know the length of the base leg and the apex angle of an isosceles triangle, the length of long equal legs will approximately be equal to the base leg length divided by the apex angle. In our solar system, there exists such an isosceles triangle. Considering a star on the sky, we can measure the view angle of that star. This view angle will change, due to the movement of Earth around the Sun. After half a year of movement, Earth would have shifted 2 astronomical unit (AU), which effectively changed the view angle of the star, see Fig 3.


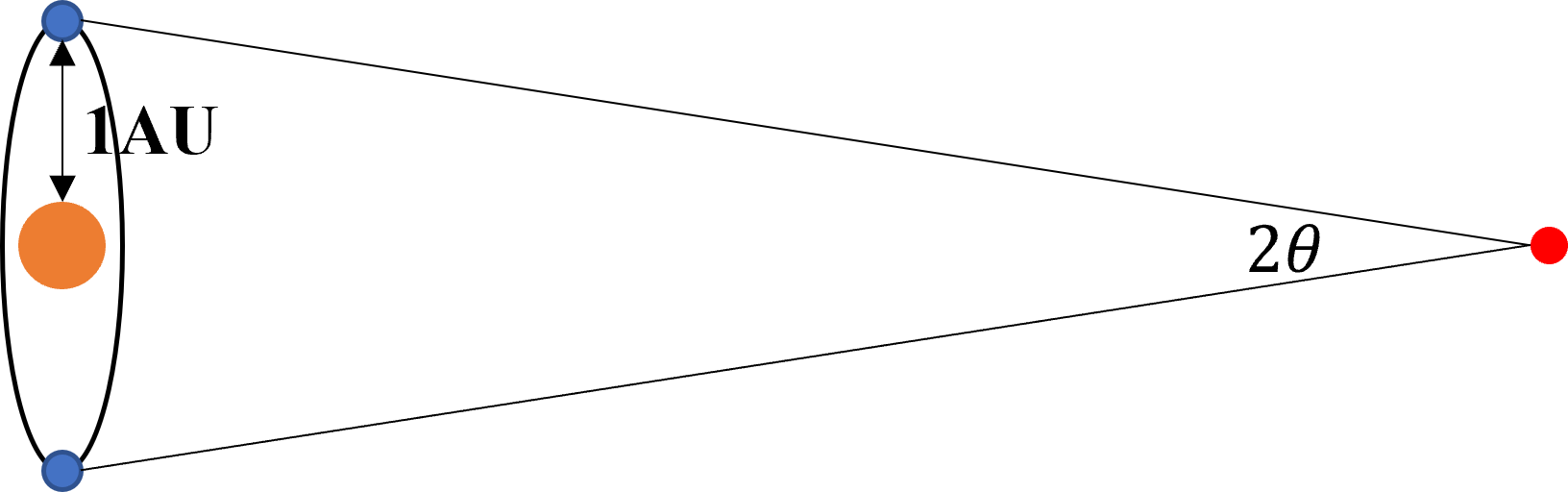
Fig 3: Stellar parallax motion in measuring the distance

By measuring the variation of the view angle of the star, the distance between that star and Earth can be calculated. If the variation of the view angle is 1 arcsecond, the measured distance is 1 parallax arcsecond (parsec), which equals 3.26 light years. The unit of parsec (pc) is usually used to describe the cosmological distance. This method is called parallax. It can provide a distance measurement up to kiloparsec (kpc) scale, due to the limitation of the precision in angle measurements.

When measuring the cosmological scale distance, this is not a pure geometric problem. Because our Universe is expanding rather than in a static state. When we receive a cosmological signal from a distant source, this signal has travelled in the space for a very long time, which means, at the time that this signal is emitted, the Universe is not as the same as the present Universe. Therefore, quantifying the cosmological scale distance involves the problem about the evolution of the Universe. In such a measurement, the observable should include the state of the Universe at signal emission time and the dynamical evolution of the Universe during the propagation of the signal.

In describing the state of the Universe, we usually use the scale factor 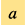, which is the scale ratio of the Universe between the past and the present. However, such a scale factor cannot be observed directly. We need to use another observable to describe the size of the Universe. Considering a cosmic signal such as a photon from a distant star, during its propagation from the source to Earth, the cosmic expansion would stretch the wavelength of the photon and induce a redshift in its observed spectrum. So we can use the observed cosmic redshift from the spectrum of the signal to obtain a cosmic scale factor. For a cosmological distance measurement, we still observe a specific object to construct a measuring method. Such an observable object should have a standard property which can be used in calibrating the distance. At present, we have developed some important methods in measuring the cosmological distance, e.g. standard candles, standard rulers and standard sirens. These methods provide us with tools to reach cosmological scale physics.

Imagining we have some candles with the same luminosity. If we put these candles at different positions away from us, the farther candle would look fainter. This is because the absolute magnitude of the candle is fixed, and the apparent magnitude of the candle is proportional to the inverse of square of the distance. Therefore, we can obtain the distance between the candle and us by comparing the apparent magnitude and absolute magnitude of the standard candle. This method is called standard candle, see Fig 4.


Fig 4: The standard candle and standard ruler in measuring the Universe (Credit: NASA)

In the Universe, observable objects that have a standard absolute magnitude can be the candidate of the standard candle. In 1908, Henrietta Swan Leavitt found that there is a strong direct relation between the luminosity and pulsation period in the Cepheid variable [14, 15], see Fig 5.


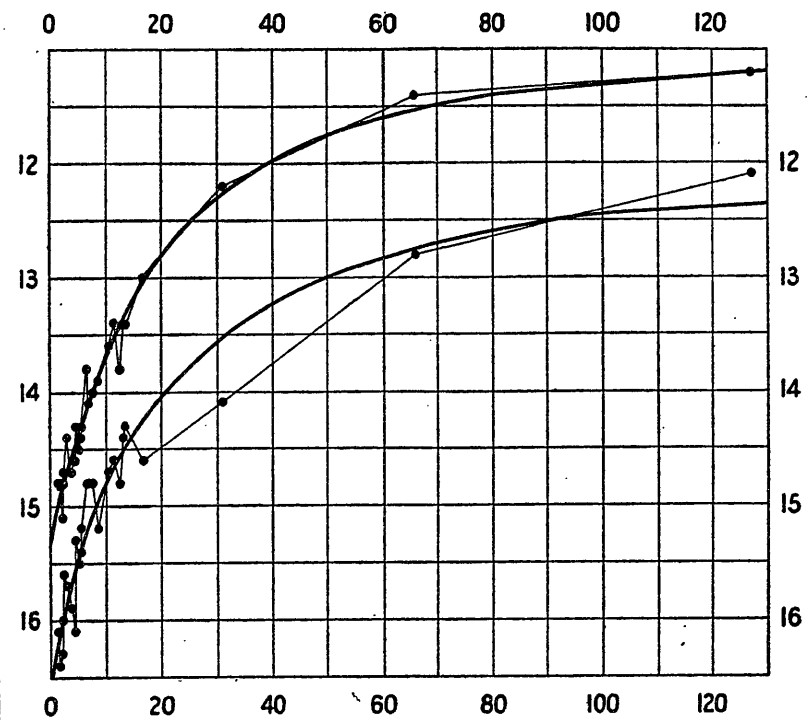
Fig 5: The relation between luminosity and pulsation period of Cepheid variable [15]

In 1930s, Walter Baade and Zwicky Fritz found the existence of supernova [16], which is proven to have a fixed peak luminosity later. By comparing the apparent magnitude and absolute magnitude of these standard candles, we can obtain their luminosity distances, which describe how the energy density of photons evolves during their propagation from the source to us. According to the spectrum of signals, we can obtain their redshifts, which provide the scale of the Universe at the signal emission time. Through the luminosity distance-redshift relation, the evolution of the Universe from the past to the present is constrained. With the help of standard candles, we can measure the Universe up to thousands of megaparsec (Mpc) scale.

For farther distance measurement, another method is needed. Considering we have some rulers with the same length, if we put these rulers at different positions away from us, the farther ruler would look smaller. This is because the absolute length of the ruler is fixed, and the observed angular separation is proportional to the inverse of the distance. Therefore, we can obtain the distance between the ruler and us by comparing the observed angular separation and their absolute length. This method is called the standard ruler, as shown in Fig 4. In our Universe, if we know the standard scale of some objects, they can be the candidate of the standard ruler. Such a scale exists in the distribution of galaxies and it is called baryon acoustic oscillation (BAO) scale. Before the CMB was formed, our Universe was in a hot plasma state. At that time, the dark matter was randomly distributed and provided a strong gravitational attraction to the baryonic matter. However, photons in the hot plasma give a strong repulsive force to the baryonic matter and induce an oscillation in the baryonic matter. With the expansion of the Universe, the Universe is cooling down and the photons decouple from the interaction with the baryonic matter and form CMB. Then this specific scale is left in the distribution of baryonic matter and later in the distribution of galaxies. This is BAO scale. By observing the angular separation of galaxies and the redshift of galaxies, we can obtain the transverse comoving distance-redshift relation, which can also help us constrain the evolution of the Universe up to gigaparsec (Gpc) scale.

With the detection of the first gravitational wave event [17], a new method emerges. It is standard sirens. The detected gravitational wave is emitted from the merger of a black hole binary. The amplitude of the gravitational wave is determined by the redshifted mass of black holes and the luminosity distance between the binary and us. Through the phase of gravitational wave, we can extract the redshifted mass of black holes. Then the luminosity distance of this binary can be obtained, see Fig 6.


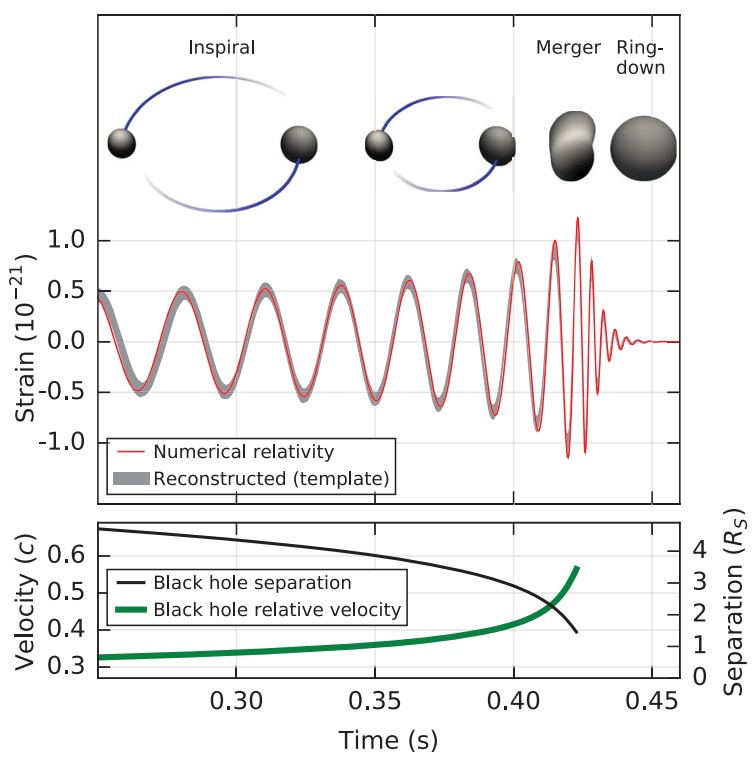
Fig 6: Gravitational wave of the first detected event GW150914 [17]

However, for constraining the evolution of the Universe, we still need to obtain the redshift of gravitational wave, which cannot be extracted from the gravitational waveform. In 2017, an event from the merger of a binary neutron stars was detected [18], which not only emitted the gravitational wave, but also the electromagnetic wave. According to this event, we can extract the luminosity distance in the gravitational wave and cosmic redshift in the electromagnetic wave. Then the relation between the luminosity distance and the redshift can constrain the cosmological model. With the development of next generation gravitational wave detectors, the standard siren can reach the Gpc scale.

Apart from above methods, we can also have some measurements in the early Universe through the CMB. Based on the Lambda cold dark matter model, we can fit the power spectrum of CMB, as illustrated in Fig 7, which gives us the estimation about the cosmological parameters [13].


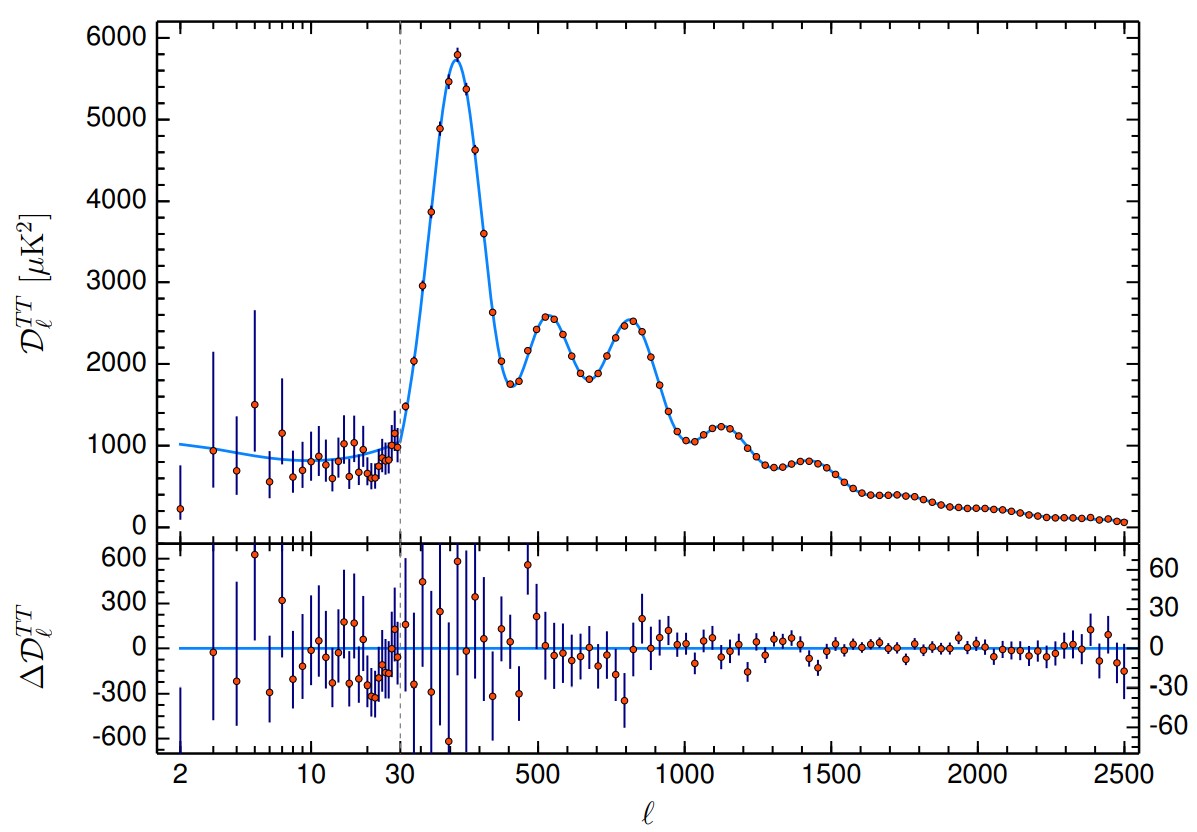
Fig 7: Planck 2018 CMB temperatures power spectrum [13]

Cosmological Crisis

In studying the evolution of the Universe, the value of the Hubble parameter is of central importance. It describes the expanding velocity of the Universe. Since Edwin Hubble found that the Universe is expanding, he first measured the Hubble parameter, which is around 500 km/s/Mpc, please refer to the slope in Fig 1, it means that the galaxy 1 Mpc away from us is leaving from us with the velocity 500 km/s. After improving observational techniques for decades, the Hubble parameter measurements have decreased from 500 km/s/Mpc to around 70 km/s/Mpc. The Hubble parameter could be measured via different methods, such as standard candles, standard rulers at low redshifts, these methods can measure the expanding velocity in the late Universe. The Hubble parameter can also be obtained from CMB by fitting the CMB power spectrum and BAO at high redshift. It provides an early Universe measurement on Hubble parameter. However, in recent years, there is a measurement inconsistency on Hubble parameter [19]. The late Universe measurements stated that the Hubble parameter is 73.0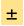1.0 km/s/Mpc, while the early Universe measurements found that it is 67.4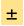0.5km/s/Mpc, see Fig 8.


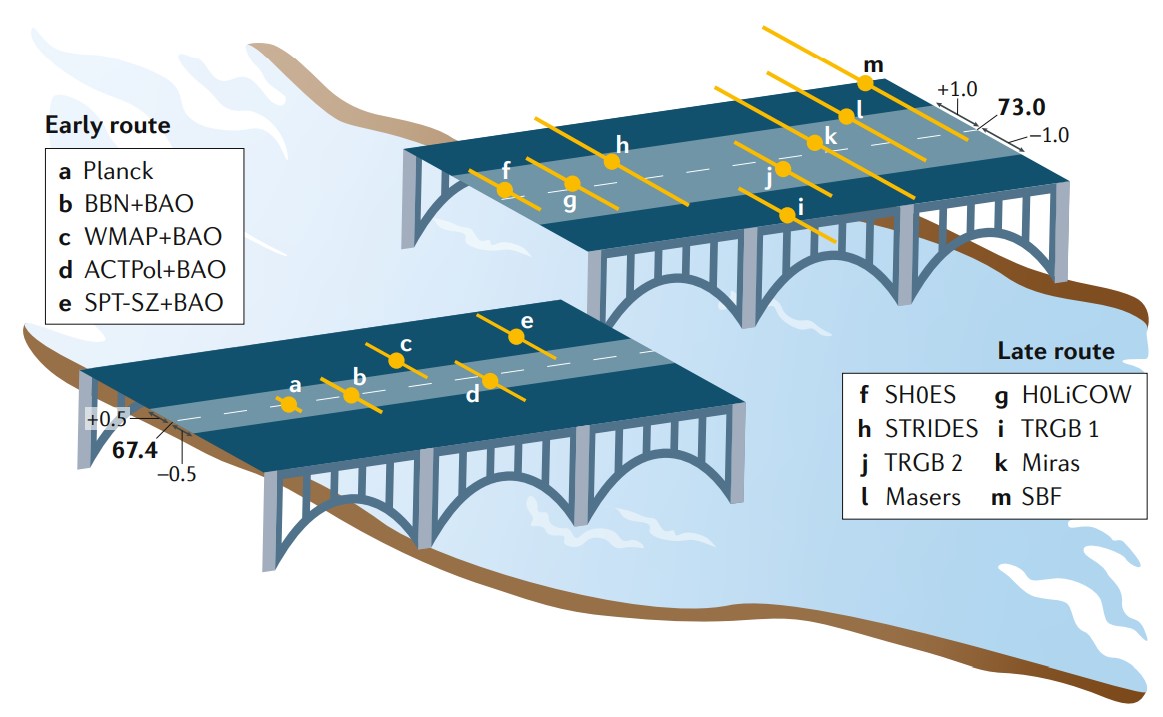
Fig 8: Hubble parameter measurements at early Universe and late Universe [19]

Although, the measurement difference in Hubble parameter between the early and the late routes is small comparing with its own value, but the measurement precision is high enough comparing with this quantification difference. Statistically, this Hubble parameter measurements difference has only reached 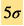significance, which means that the possibility of this measurement difference caused by technical error is only around 2.9×10−7.This possibility is extremely small, so there should be some mechanisms causing such a difference in Hubble parameter measurements. This issue has become a cosmological crisis in modern cosmology, which is also known as Hubble tension.

Apart from the Hubble tension, there still exists some other problems in modern cosmology [20], such as the inconsistency in different matter density measurements (also known as 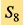tension), the inconsistency in different cosmic dipole measurements, etc. These problems drive us to find a better cosmological model and understand the fundamental physics behind the evolution of the Universe.

Cosmological Standard Timer: a novel way to measure the Universe

In understanding the physics behind the cosmological crisis, our strategy is to construct a new method to measure the Universe by tracking the cosmic evolution from the early Universe to the present Universe. After having a detailed understanding of the history of the Universe, a better cosmological model can be built.

In the above discussions about measurement methods, the evolution of the Universe is constrained by the distance-redshift relation, where cosmic redshift provides the scale of the Universe at the time that signals were emitted, and the cosmic distance provides the information about cosmic evolution from the signal emission time to the present. A more direct method in studying the evolution of the Universe is to know the evolution of the scale factor 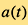. However, as that scale factor cannot be observed directly, the evolution of the cosmic redshift 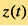is studied instead. The relation between scale factor and cosmic redshift is .

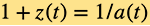In our Universe, there are a lot of dynamical systems each evolves according to their intrinsic mechanisms. A long period of evolution has effectively changed the status of such dynamical systems. By studying the intrinsic mechanism in these dynamical systems, we can obtain their physical evolution time from the initial status to a later status. As the evolution of the dynamical system is independent from cosmic evolution, their physical evolution time can be viewed as an independent measurement on the cosmic time. When these dynamical systems evolve, some cosmic signals, such as electromagnetic waves, gravitational waves, are emitted. During the propagation of these signals from their sources to us, the cosmic expansion stretches their wavelength, which leaves the cosmic redshift in the spectrum of signals. Therefore, when we observe cosmic signals from a specific dynamical system, the cosmic redshift can be extracted from observed signals, and the physical evolution time can be obtained by comparing observed status with the initial status of the dynamical system. As a result, we can construct a redshift-time relation, which tells us the evolution of cosmic redshift 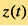. In the above mechanism, the dynamical systems work as a standard timer in the Universe, which tells us the status of the Universe at a different physical time.

The above mentioned is the basic idea of the standard timer. For constructing a practical standard timer, we need to choose a specific dynamical system. To study the evolution of the Universe from the early epoch to the late epoch, such a dynamical system should exist since the early Universe. However, the usual astrophysical objects such as the stars or astrophysical black holes only exist at the late Universe. Therefore, we consider a special kind of black holes to construct a standard timer, it's called primordial black holes (PBHs).

A black hole is usually considered as the remnant of the gravitational collapse of a dying star. This kind of black holes is called astrophysical black holes. The astrophysical black holes can only exist in the late Universe, because stars only exist in the late Universe. The mass of astrophysical black hole is usually three times larger than the mass of the Sun, so that the gravitational attraction is large enough to overcome the repulsive force between fundamental particles. However, the PBH is different. The PBH was first proposed by Stephen Hawking and Bernard Carr in 1974 [21] and that it was formed from the gravitational collapse of the primordial perturbations. So, PBHs can exist from the early Universe to the present as there is not enough repulsive force at the early Universe. Thus, the mass of PBHs can be any values above 10-5g [21].

After choosing PBHs to construct a standard timer, cosmic signals from PBHs are crucial in the analysis. However, it's a little weird to say that signal emits from black holes. In our mind, a black hole is usually black and has a formidable gravitational attraction where not even light can escape. So how could a cosmic signal escape from a black hole and arrive on Earth? Well, a black hole is not black. In 1974, Stephen Hawking pointed out that even black holes can emit radiation and particles [22, 23] known as Hawking radiation. Therefore, black holes can also emit signals. The problem is, however, the power of Hawking radiation, which is proportional to the inverse of square of the black hole mass, is considered extremely weak. Generally, the mass of an astrophysical black hole is three times larger than the mass of the Sun, so the power of Hawking radiation is so weak that we were unable to observe it until now. The PBH changes the story. The mass of PBHs can be very small, which means that Hawking radiation from PBHs can be strong enough for detection. Apart from Hawking radiation, the gravitational effect of a black hole can also be viewed as an important cosmic signal, especially the gravitational waves emitted from a binary black hole. If the mass of a binary black hole is large enough, the emitted gravitational wave can be detected.

The first dynamical system we study is the light PBHs cluster [24]. In this dynamical system, it has a standard initial status, which is the initial mass function of PBHs. Because PBHs were formed from the same primordial perturbations, the initial mass function in each PBHs cluster should be the same. With the emission of Hawking radiations from PBHs, PBHs lose their mass and the lighter PBH loses much more mass than the heavier PBH. This mechanism distorts the PBH mass function, and the physical evolution time can be extracted by studying the evolution from the initial mass function to the later mass function. Then Hawking radiation propagates from the PBHs cluster to us, the cosmic expansion would decay its energy density and stretch its wavelength, which results in observed Hawking radiation spectrum having a small amplitude and being redshifted. Although the amplitude of observed Hawking radiation spectrum is small, the PBH cluster has a large number of PBHs, so the emitted Hawking radiation is strong enough for detections. By comparing the redshifted spectrum with standard spectrum from PBHs cluster, the cosmic redshift can be extracted. By combining the obtained physical evolution time and cosmic redshift from a PBHs cluster, we can know cosmic redshift at a cosmic time. After observing a lot of PBHs clusters, the relation between redshift and time can be obtained and used in constraining the evolution of the Universe, see Fig 9 for demonstration.


Fig 9: The standard timer in light PBH clusters

The second dynamical system we study is the PBH binaries [25]. In this dynamical system, the standard initial status is the initial probability distribution on major axis and eccentricity of the binaries. With motion of PBHs in binary, the gravitational effect causes perturbations in spacetime, which produces the gravitational waves. The emitted gravitational wave takes energy away from the PBH binary and changes its major axis and eccentricity. Such a mechanism would change the probability distribution on major axis and eccentricity. Therefore, the physical evolution time between the initial status and the later status can be extracted by studying the evolution of the probability distribution on major axis and eccentricity. During the propagation of gravitational waves from PBHs binaries to us, the expansion of the Universe stretches the wavelength of gravitational waves and leave the cosmic redshift in observed gravitational waves. This redshift in gravitational waves would cause a coordinate shift in observed probability distribution on major axis and eccentricity. Therefore, cosmic redshift can be extracted by comparing the observed probability distribution with the standard initial probability distribution. The relation between cosmic redshift and physical evolution time is then calibrated. After detecting a lot of gravitational wave events from the PBHs binary system, the cosmic redshift will be calibrated at different cosmic time from the early Universe to the present, which further gives us the evolution of the cosmic redshift and scale factor, see Fig 10 for demonstration.


Fig 10: The standard timer in PBH binaries

In the above discussion, we focus on constructing the standard timer in PBHs systems. Actually, there are a lot of cosmological dynamical systems which can be the candidate of the standard timer. If a cosmological dynamical system has a standard initial status and exact evolution mechanism, the physical evolution time in this system can be viewed as an independent measurement on cosmic time. Meanwhile, the expansion of the Universe leaves cosmic redshift in their observables. Then the relation between cosmic redshift and physical time can be obtained by studying this kind of cosmological dynamical systems, just like working as a standard timer in the Universe. For example, for the first-generation stars, if we know their initial mass function and star formation rate, by studying their population evolution, a new kind of standard timer can be constructed in measuring the late Universe.

With the help of these measurement techniques, namely standard candles, standard rulers, standard sirens and standard timers, the fundamental mystery of the Universe will be revealed, and we, the humans as a whole will finally understand the Universe which we inhibit.

References:


  1. Einstein, Albert. "Cosmological considerations on the general theory of relativity." Sitzungsber.Preuss.Akad.Wiss.Berlin (Math.Phys.),(1917): 142-152.
  2. Friedmann, Alexander. "Über die krümmung des raumes." Zeitschrift für Physik 10.1 (1922): 377-386.
  3. Friedmann, Alexander. "Über die Möglichkeiteiner Welt mitkonstanternegativerKrümmung des Raumes." Zeitschrift für Physik 21.1 (1924): 326-332.
  4. Lemaître, Georges. "Un Univershomogène de masse constante et de rayon croissant rendantcompte de la vitesse radiale des nébuleuses extra-galactiques." Annales de la Société scientifique de Bruxelles. Vol. 47. 1927.
  5. Hubble, Edwin. "A relation between distance and radial velocity among extra-galactic nebulae." Proceedings of the national academy of sciences 15.3 (1929): 168-173. [6]. Gamow, George. "Expanding universe and the origin of elements." Physical review 70.7-8 (1946): 572.
  6. Alpher, Ralph A., Hans Bethe, and George Gamow. "The origin of chemical elements." Physical Review 73.7 (1948): 803.
  7. Penzias, Arno A., and Robert Woodrow Wilson. "A measurement of excess antenna temperature at 4080 Mc/s." The Astrophysical Journal 142 (1965): 419-421.
  8. Akrami, Yashar, et al. "Planck 2018 results-IV. Diffuse component separation." Astronomy & Astrophysics 641 (2020): A4.
  9. Freeman, Kenneth C. "On the disks of spiral and S0 galaxies." The Astrophysical Journal 160 (1970): 811.
  10. Rubin, Vera C., and W. Kent Ford Jr. "Rotation of the Andromeda nebula from a spectroscopic survey of emission regions." The Astrophysical Journal 159 (1970): 379.
  11. Riess, Adam G., et al. "Observational evidence from supernovae for an accelerating universe and a cosmological constant." The Astronomical Journal 116.3 (1998): 1009.
  12. Aghanim, Nabila, et al. "Planck 2018 results-VI. Cosmological parameters." Astronomy & Astrophysics 641 (2020): A6.
  13. Leavitt, Henrietta S. "1777 variables in the Magellanic Clouds." Annals of Harvard College Observatory 60 (1908): 87-108.
  14. Leavitt, Henrietta S., and Edward C. Pickering. "Periods of 25 Variable Stars in the Small Magellanic Cloud." Harvard College Observatory Circular 173 (1912): 1-3.
  15. Baade, Walter, and Fritz Zwicky. "On super-novae." Proceedings of the National Academy of Sciences 20.5 (1934): 254-259.
  16. Abbott, Benjamin P., et al. "Observation of gravitational waves from a binary black hole merger." Physical review letters 116.6 (2016): 061102.
  17. Abbott, B. P., et al. "Multi-messenger Observations of a Binary Neutron Star Merger." The Astrophysical Journal 848.2 (2017).
  18. Riess, Adam G. "The expansion of the Universe is faster than expected." Nature Reviews Physics 2.1 (2020): 10-12.
  19. Abdalla, Elcio, et al. "Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies." Journal of High Energy Astrophysics (2022).
  20. Carr, Bernard J., and Stephen W. Hawking. "Black holes in the early Universe." Monthly Notices of the Royal Astronomical Society 168.2 (1974): 399-415.
  21. Hawking, Stephen W. "Black hole explosions?." Nature 248.5443 (1974): 30-31.
  22. Hawking, Stephen W. "Particle creation by black holes." Euclidean quantum gravity. 1975. 167-188.
  23. Cai, Yi-Fu, et al. "Cosmological Standard Timers from Unstable Primordial Relics."arXiv:2112.10422 (2021).
  24. Ding, Qianhang. "Cosmological Standard Timers from Primordial Black Hole Binaries." arXiv:2206.03142 (2022).

Author:
Mr Qianhang Ding, PhD Candidate, Department of Physics, The Hong Kong University of Science and Technology
January 2023