使用宇宙标准计时器测量宇宙


自人类于地球诞生，我们一直尝试了解我们所在的宇宙。经过了数千载的观察和思考，我们已经发展了一套宇宙学标准模型，可让我们更好地描述宇宙热大爆炸以来的演化。然而，随著科技进步和精确测量技术的发展，更多结果显示观测和理论之间存在著矛盾，其中哈勃常数疑难，便是现代宇宙学中的一个迫在眉睫、亟待解决的问题。

解决问题，必先了解问题。为化解上述宇宙学危机，科学家提出了多种方法，包括修正基础物理学和观测上的系统偏差。另一边厢，我们也为测量宇宙提出了一个名为「宇宙标准计时器」的新方法。采用此方法来研究宇宙动力学系统的演化，可让我们了解宇宙在不同时期的状态。掌握更多宇宙演化的信息，将助我们更好地理解宇宙学模型。

宇宙的演化

现代宇宙学始自于将引力描述为时空几何广义相对论。1917年，阿尔伯特·爱因斯坦（Albert Einstein）以广义相对论为基础，建立了他的宇宙学模型[1]，并据此描述了一个静态的宇宙。然而在宇宙扰动之下，这个静态宇宙学模型是不稳定的。在二十世纪二十年代，亚历山大·弗里德曼（Alexander Friedmann）提出了广义相对论的宇宙学解[2, 3]，认为视乎物质密度和时空曲率，宇宙既可能是膨胀的，也可能是收缩的。与此同时，乔治·勒梅特（Georges Lemaître）独立提出了相对论化的宇宙学方程，并指出可能是一个原初原子的爆炸引致宇宙诞生[4]。

直到1929年，宇宙演化的问题才首次获得解答。埃德温·哈勃（Edwin Hubble）发现遥远星系的光谱发生红移 [5]，这意味著这些星系正在远离我们，而且远离的速度与它们和地球的距离成正比，这就是著名的哈勃定律（见图1）。


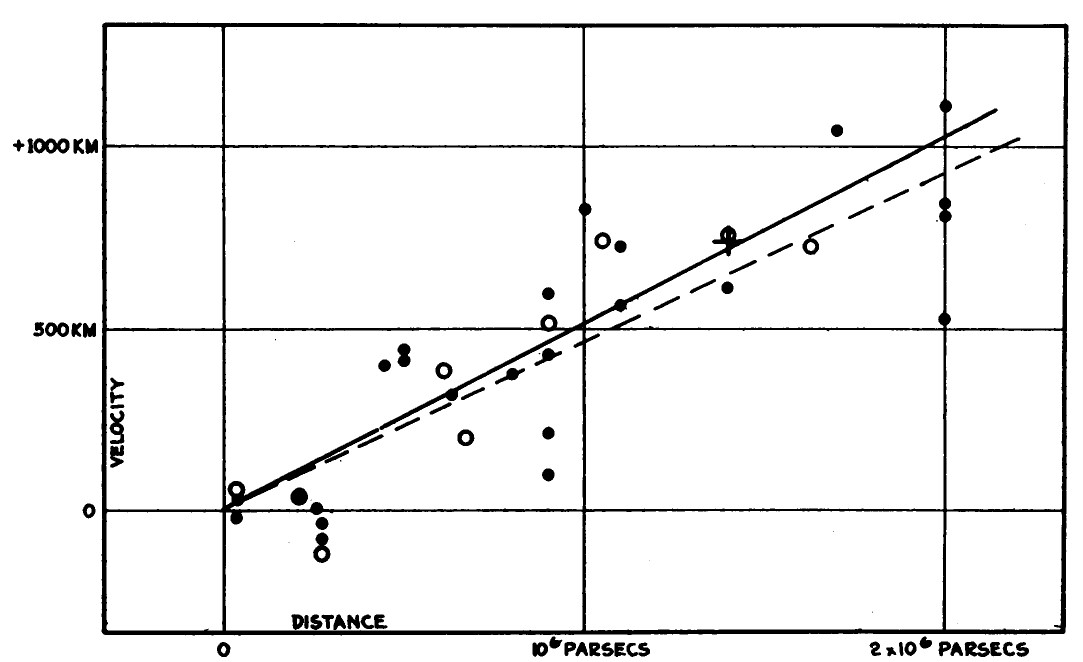
图1: 银河外星云的速度与距离关系[5]

所以，哈勃的观测证明了我们的宇宙正在膨胀。为了描述宇宙的膨胀速度，量化宇宙膨胀，我们把星系速度与距离关系的斜率定义为哈勃参数或称之为哈勃常数。

乔治·伽莫夫（ George Gamow ）通过研究相对论宇宙学理论和哈勃的观测所得，提出宇宙在最初始之时处于很热并且高密度的状态，但随著宇宙的膨胀，初始的等离子态慢慢的冷却并且形成了最初的元素[6, 7]。但是这一对宇宙的描述并没有被其他的物理学家接受。提出稳态宇宙学模型的物理学家弗雷德·霍伊尔（Fred Hoyle）在一个BBC的访谈中，戏称伽莫夫的理论为「大爆炸」。

之后的十几年，热大爆炸理论和稳态理论之间的争论旷日持久。直到1965年，射电天文学家阿诺·彭齐亚斯（Arno Penzias）和罗伯特·威尔逊（(Robert Wilson）发现在空中存著一个均匀的微波波段背景噪声，其后被证明是宇宙微波背景[8]（见图2）。


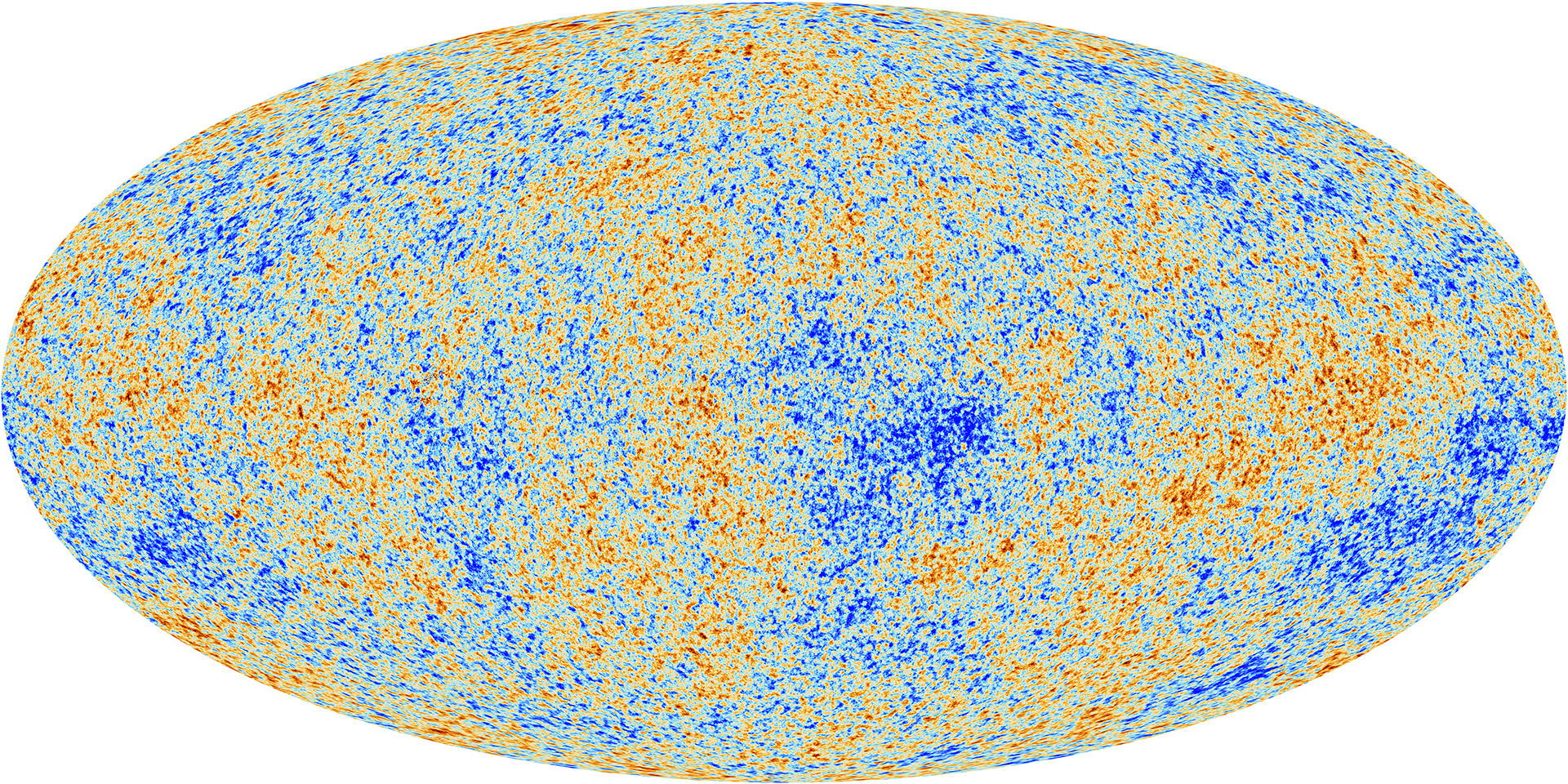
图2: Planck 卫星测量的宇宙微波背景[9]

由于宇宙微波背景可以在宇宙早期的初始高温高密度状态的冷却过程中自然形成，宇宙微波背景的存在证明了热大爆炸理论成立，热大爆炸模型亦因而变成了宇宙学标准模型的基础。

过去几十年，随著精确宇宙学的不断发展，一些重要的宇宙学现象亦陆续被发现，包括除了我们已知的宇宙外还存在著一个黑暗宇宙。1970年，薇拉·鲁宾（Vera Rubin），肯特·福特（Kent Ford）和肯·弗里曼（Ken Freeman）测量了银河系的旋转曲线，但测量结果与他们所预期的表现并不相符[10, 11]。根据观测结果，科学家提出了一个宇宙存在一种特殊物质的假说，这种物质只参与引力相互作用，并不发光，因此也被称为「暗物质」。1998年，科学家在研究地球附近Ia类超新星时发现，宇宙的膨胀正在加速[12]，故此应有一种特殊能量产生排斥力来加速宇宙的膨胀，而这种能量被称为「暗能量」。为了知道这些不同的成分在宇宙中的所占比例，2009年，普朗克卫星发射升空探测宇宙微波背景的各向异性，最终结果于2018年发表[13]。结果显示，目前我们已知的物质只占宇宙总能量的5%，暗物质占26.5%，暗能量占68.5%。

现在我们已经建立了宇宙学标准模型（或称Lambda冷暗物质模型，Lambda指暗能量）。根据这个模型，宇宙的演化取决于其不同的成分，其中物质（包括正常物质和暗物质）引起的吸引力会减低宇宙的膨胀速度，而暗能量所产生的排斥力则会加快宇宙的膨胀。宇宙的总能量密度决定了宇宙的膨胀速度，或者哈勃参数。如果我们知道物质和暗能量演化的动力学，或许我们就可以精确地测量哈勃参数，进而更好地了解宇宙的过去和未来。

测量宇宙

欲研究宇宙的演化，先须测量宇宙，而测量的第一步，就是量丈宇宙的距离。然而这项工作殊不简单，要懂得以由小见大，知微见著。方法之一是应用三角学，一个等腰三角形如果已知底长和顶角角度，求其腰长，那么以底长除以顶角角度就可得出其大约长度。在我们的太阳系中就存在著这么一个等腰三角形。如果我们看著天空中的一颗恒星，我们可以测量这颗恒星相对于我们的视角。而由于地球环绕太阳公转，这颗恒星的视角也在不断变化。经过半年的公转，地球已在太阳系中移动了两个天文单位，这有效地改变了这颗恒星相对于我们的视角（见图3）。


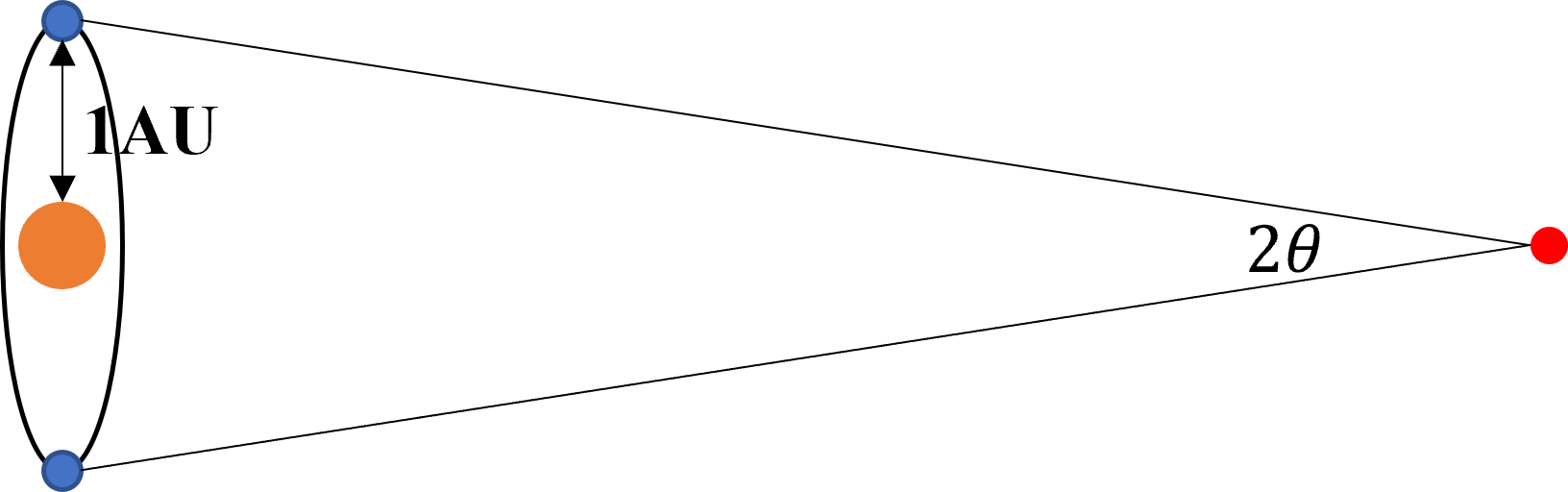
图3: 通过恒星的视差来测量距离

通过测量恒星视角的变化，我们可以求得恒星与地球的距离。如果说视角的变化是1弧秒，那么测量到的距离就是1秒差距，即等于3.26光年。秒差距这个单位也常用于描述宇宙学距离。这种基于恒星视角测量距离的方法被称之为视差法，它可以用来测量大致几千秒差距的距离。然而由于角度测量的精度限制，更远的距离就难以通过视差法测量。

不过，若要测量更长的宇宙学距离，那就不是一个纯粹的几何学问题了。因为我们的宇宙是处在一个膨胀而不是静止的状态。当接收到遥远的宇宙学信号时，这个信号已经在空间传播了一段很长的时间。换言之，这信号被发出时，当时宇宙和我们现在的宇宙并不一样。所以，测量宇宙学距离也牵涉及宇宙是如何演化的问题。因此在这样的测量中，被观测的量应包含宇宙在信号发出时的状态和在信号传播过程中的动力学演化。

在描述宇宙状态的时候，我们通常使用标度因子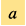，它是过去宇宙和现在宇宙的尺度比例。然而标度因子不能直接用来观测，我们需要使用其他的可观测量来描述宇宙的尺度。当我们考虑一个宇宙学信号，例如一个来自遥远恒星的光子，在它从信号源传播到地球的过程中，宇宙膨胀将会拉长光子的波长，这会导致观测光谱红移，而我们可以使用信号谱中观测到的宇宙学红移来得到宇宙的标度因子。就宇宙学距离测量而言，我们需要通过观测特定物体来构建测量方法。这个特定的观测物体应有一个标准属性用做距离校准。目前我们已经发展了多种测量宇宙学距离的方法，例如标准烛光、标准尺子，以及标准汽笛，这都是让我们理解宇宙尺度物理的工具。

假设我们有一些亮度相同的蜡烛，如果从我们本身的位置开始，把这些蜡烛放在不同的位置，那么蜡烛距离我们越远，烛光看来就越黯淡。这是由于烛光的绝对亮度是固定的，而烛光的视亮度是蜡烛与我们之间距离的平方反比。所以通过比较标准烛光的视亮度和绝对亮度，就可以测算出它与我们的距离，这种方法被称之为标准烛光法（见图4）。


图4: 通过标准烛光和标准尺子测量宇宙（图片来源: NASA）

在宇宙中，具有标准绝对亮度的可观测物体都可以作为标准烛光的候选者。1908年，亨丽爱塔·斯万·勒维特（Henrietta Swan Leavitt）发现在造父变星的亮度和脉动周期中存在很强烈的直接关联[14, 15]（见图5）。


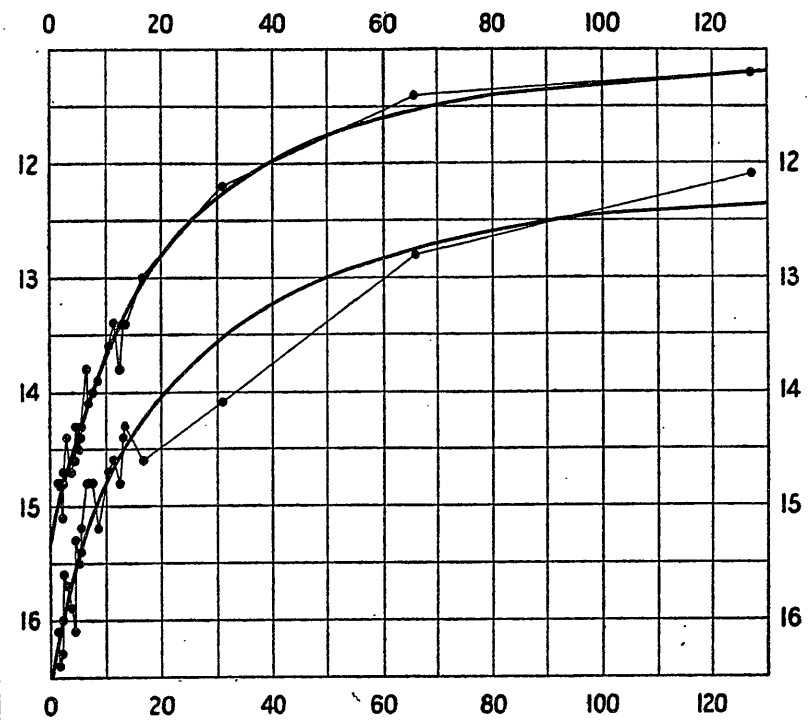
图5: 造父变星的亮度与脉动周期的关系[15]

二十世纪三十年代，沃尔特·巴德（Walter Baade）和弗里茨·兹威基（Zwicky Fritz）发现超新星[16]，超新星其后被证明具有固定峰值的亮度。通过比较这些标准烛光的视亮度和绝对亮度，我们可以得出它们的亮度距离，这是一个描述光子的能量密度从源头传播到我们所在位置过程中如何演化的一个物理量。通过其信号光谱，我们也可以获得它们的红移值，这为我们提供了宇宙在信号被发射时的尺度。通过亮度距离和红移的关系，宇宙从过去到现在的演化过程也被限制住了。有了标准烛光的帮助，我们就可以测量出高达几亿秒差距的宇宙距离。

对于更远距离的测量，我们需要动用其他的方法。假设我们有一些相同长度的尺子，如果从我们本身的位置开始，把这些尺子放在不同的地方，那么距离我们越远的尺子看起来就会越小。这是因为尺子的绝对长度是固定，而观测到的角间距是距离的反比。所以通过比较观测到的角间距和它们的绝对长度，就可得出尺子和我们的距离(见图4)。在宇宙中，一旦知道物体的标准尺度，该物体就可以选作为标准尺子。星系的分布中存在著这样的尺度，称为重子声学振荡尺度。在宇宙微波背景形成前，宇宙处于热等离子态。那时候，宇宙中的暗物质随机分布，对重子物质产生强大的吸引力。然而，热等离子体中的光子却对重子物质产生强大的排斥力，并且引起重子物质的振荡。宇宙不断膨胀，温度也随之慢慢下降，光子开始从重子物质的相互作用中退耦，形成宇宙微波背景。这时候，那把特殊的尺度留在了重子物质的分布中，其后留在了星系的分布中，那就是前文提到的重子声学振荡尺度。通过观测星系之间的角间距和它们的红移，我们能掌握横向共动距离和红移的关系，进而帮助我们限制宇宙的演化到达数十亿秒的差距。

当探测到第一个引力波事件后[17]，测量宇宙又有了一种名为标准汽笛法的新方法。被探测到的引力波由一个双黑洞合并发出，其振幅取决于双黑洞的红移质量和从黑洞到我们的亮度距离。通过引力波的相位，我们可以取得黑洞的红移质量，继而得出双黑洞的亮度距离（见图6）。


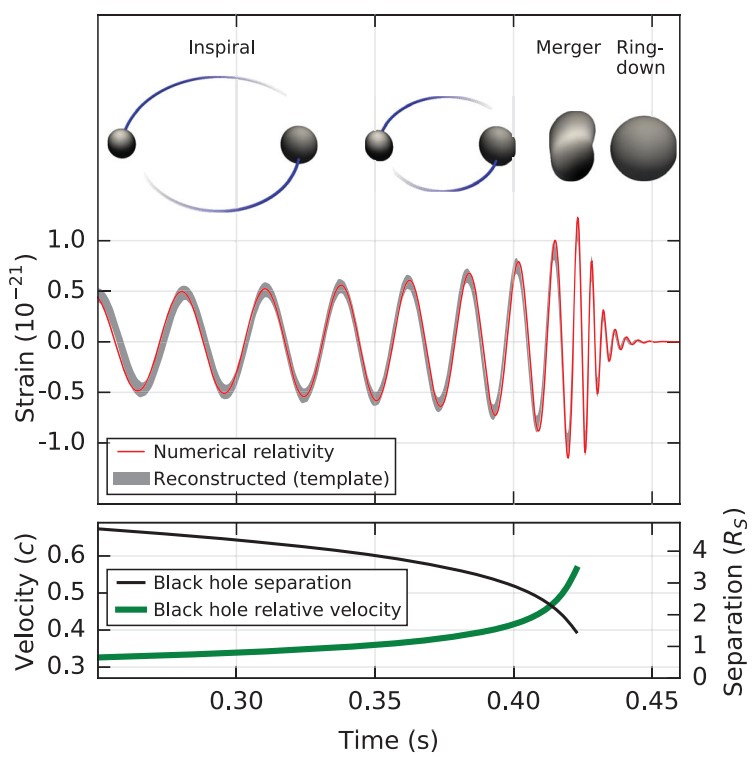
图6: 第一个观测到的引力波事件GW150914 [17]

但是，为了限制宇宙的演化，我们仍需获得引力波源的红移，但这并不能直接从引力波中提取。2017年，科学家观测一例双中子星合并事件[18]。合并过程不仅辐射出引力波，也辐射出电磁波，让我们既可以从引力波中提取亮度距离的信息，也可以从电磁波中提取宇宙红移的信息，而亮度距离和红移的关系又能帮助我们限制宇宙学模型。随著引力波探测器的发展更代升级，标准汽笛法可以测量的距离尺度高达数十亿秒差距。

除了上述方法，我们也可以通过宇宙微波背景进行一些关于早期宇宙的测量，例如根据Lambda冷暗物质模型拟合宇宙微波背景的功率谱（见图7），从而估算宇宙学参数 [13]。


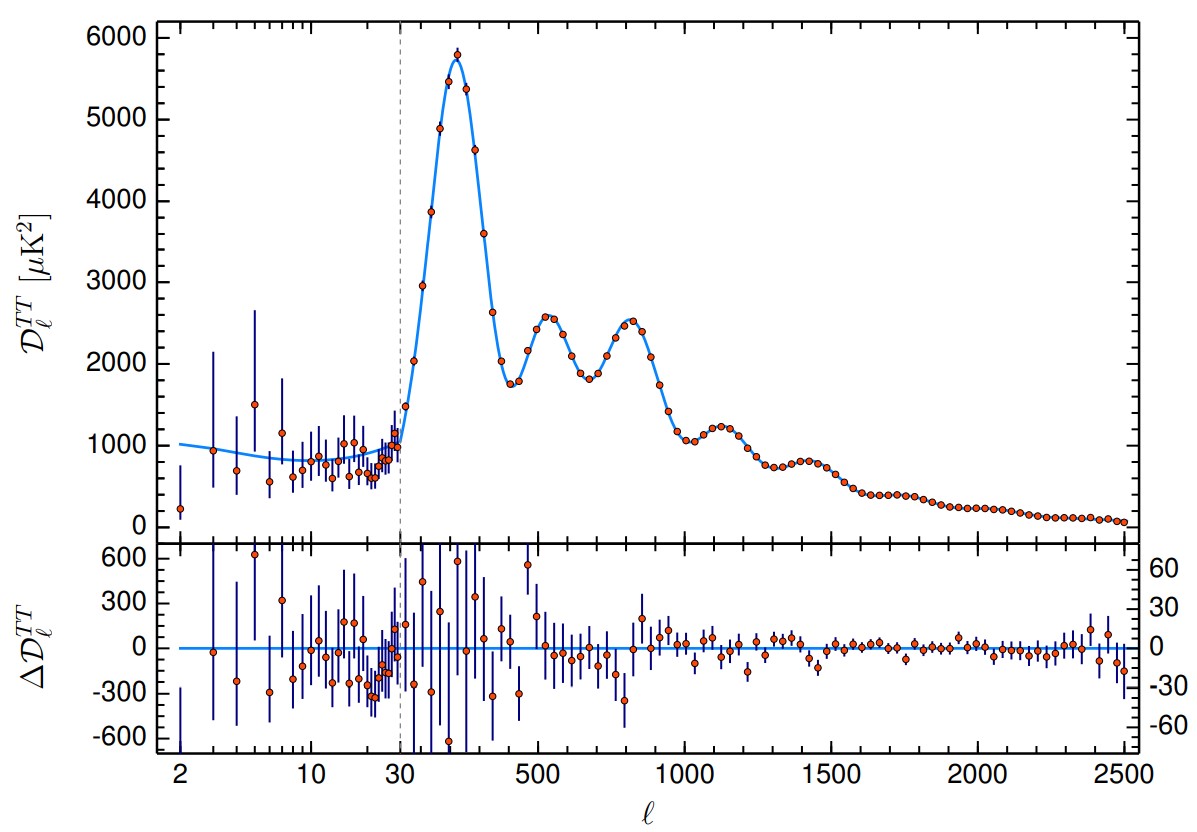
图7: Planck 2018宇宙微波背景辐射温度功率谱 [13]

宇宙学危机

在研究宇宙演化的过程中，哈勃参数的数值至关重要，参数的数值代表著宇宙的膨胀速度。当哈勃发现宇宙正在膨胀后，他先测量了哈勃参数，得出500km/s/Mpc这个约数（见图1中的斜率），这代表距离我们一百万秒差距的星系正在以500km/s的速度远离我们。随后的几十年观测技术不断提升，哈勃参数的测量值已经从500km/s/Mpc降到了大约70km/s/Mpc。测量哈勃参数标准烛光或者低红移标准尺子等多种方法，而且都可以用来测量晚期宇宙的膨胀速度。此外，也可以通过拟合宇宙微波背景的功率谱和高红移重子声学振荡取得哈勃参数，用来测量早期宇宙。不过近年来，科学家发现哈勃参数的测量并不一致[19]，晚期宇宙的测量得出的哈勃参数为73.0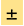1.0 km/s/Mpc，而早期宇宙的测量则为67.4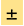0.5 km/s/Mpc（见图8）。


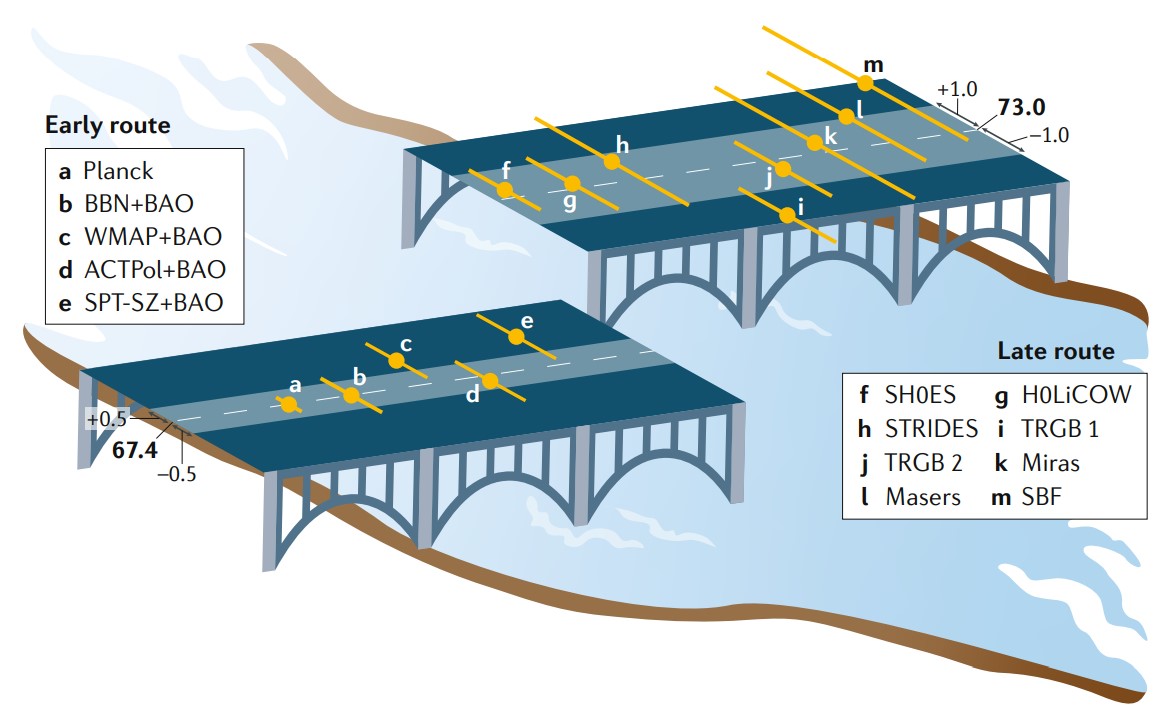
图8: 哈勃参数在早期宇宙和晚期宇宙的测量值[19]

虽然哈勃参数通过早期和晚期宇宙途径测出的结果两者之差相对于自身值来说不大，但是测量的精度相对于测量上的偏差则算高。统计学上来说，哈勃参数的测量差距达到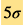 的置信度，意味著这种偏差是由测量误差导致的可能性大约是2.9×10−7。由于这种可能性太小，故应该是因为存在著某些机制而导致哈勃参数出现了这一偏差。这个问题成为现代宇宙学的危机，称为哈勃常数疑难。

除了哈勃常数疑难，现代宇宙学中也有其他问题有待解决[20]，例如不同物质密度测量不一致，不同的宇宙学极化测量不一致。这些问题促使我们研发更好的宇宙学模型，并探索隐藏在宇宙演化背后的基础物理。

宇宙标准计时器：一种测量宇宙的新方法

为了理解藏身在宇宙学危机背后的物理，我们得构建一种新的宇宙测量法，来追踪宇宙早期至今的演化。只有透过深入理解宇宙的演化历史，才能建立一个更好的宇宙学模型。

在上述关于测量方法的讨论中，宇宙的演化受距离和红移的关系所限制。红移为我们提供了宇宙在信号发出时的尺度，距离则提供了宇宙从信号发出至今的演化信息。虽然从了解尺度因子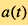的演化入手是更直接的研究宇宙演化的方法，但由于尺度因子不能被直接观测得到，科学家便以研究宇宙红移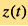的演化来作为替代。尺度因子和宇宙红移的关系为.

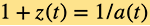宇宙中存在著许多动力学系统，各自按其内在机制而演化。经过一段长时间的演化，这些系统的状态已起了实质的变化。通过研究其演化的内在机制，我们可以获得系统从初始状态演化至后期状态的物理演化时间。由于这些动力学系统的演化是独立于宇宙演化的，因此它们的物理演化时间可视作为一个独立的宇宙时间测量。这些动力学系统在演化时，会释放一些宇宙学信号，例如电磁波和引力波。而在这些信号发出至传递到我们的过程中，宇宙膨胀将其波长伸拉，同时在信号谱中留下宇宙红移。所以，当我们观测到某个特定的动力学系统的宇宙信号时，便可以从信号中提取宇宙红移，并通过比较动力学系统的初始态和观测状态，得出它们的物理演化时间。据此，我们可以构建一个红移时间关系，这也告诉了我们宇宙红移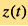是如何演化的。在上述的机制中，动力学系统就像是宇宙中的一个标准计时器一样工作，告诉我们宇宙在不同时刻的物理状态。

以上就是标准计时器的基本构思。为构建一个实用的标准计时器，研究宇宙从早期到晚期的演化，我们需要选择一个特定的动力学系统，而这个系统应该从宇宙早期一直存在至今。不过，常见的天体，例如恒星和天体物理黑洞，只存在于晚期宇宙。故此，构建标准计时器就得采用一种特殊的黑洞，就是原初黑洞。

恒星死亡后，引力坍缩形成黑洞，称为天体物理黑洞。由于恒星只存在于晚期宇宙，天体物理黑洞也只能存在于晚期宇宙。天体物理黑洞的质量一般大于太阳质量的三倍，所产生的引力足以凌驾基本粒子间的排斥作用力。但是原初黑洞不同，被斯蒂芬·霍金（Stephen Hawking）和伯纳德·卡尔（Bernard Carr）于1974年率先提出原初黑洞[21]，指它由原初扰动的引力坍缩所形成，故此是从早期宇宙一直存在至今的天体。由于在早期宇宙没有足够的排斥作用力，原初黑洞的质量可以是大于10-5克的任何值[21]。

选定原初黑洞来构建标准计时器后，原初黑洞发出的宇宙学信号便成为重要的分析元素。但是，黑洞会发出信号这点说来有点奇怪，因为在我们的观念中，黑洞是漆黑的而且有著可怕的吸引力，甚至连光都逃脱不了。要是这样的话，宇宙信号又是如何逃离黑洞传到地球呢?事实上，黑洞其实不是黑的。1974年，霍金发表研究，指即使是黑洞也能发出辐射和粒子[22, 23]，这就是著名的霍金辐射。换言之，黑洞也能发出信号，只是黑洞质量的平方反比，功率非常微弱。一般来说，天体物理黑洞的质量大于太阳质量的三倍，黑洞发出的霍金辐射非常微弱，以至于我们时至今天都没有观测得到。然而，原初黑洞改变了这个看法。由于原初黑洞的质量可以非常小，所发出的霍金辐射的功率强到足以被观测到。除了霍金辐射，黑洞产生的引力效应也可被视作一种重要的宇宙学信号，尤其是源自双黑洞系统的引力波。如果双黑洞的质量足够大，辐射出的引力波也是可以被观测到的。

我们研究的第一个动力学系统是小质量原初黑洞群[24]。这个动力学系统具有标准的初始状态，即原初黑洞的初始质量函数。由于原初黑洞形成于相同的原初扰动的引力坍缩，故每个原初黑洞群的初始质量函数都应该是一样的。随著原初黑洞发出霍金辐射，其质量慢慢降低。此外，相对于更重的原初黑洞，小质量原初黑洞的质量损失更大。这种质量损失会改变原初黑洞的质量函数，通过研究质量函数从初始到后期的演化，我们从中就可以提取它们的物理演化时间。霍金辐射从原初黑洞群传递到我们的过程中，宇宙膨胀将辐射的能量密度稀释并且伸拉其波长，导致观测到的霍金辐射振幅比较小，而出现红移。尽管霍金辐射谱的振幅比较小，但是原初黑洞群有著大量的原初黑洞，因此发出的霍金辐射依然可被观测得到。通过比较红移后的霍金辐射和标准霍金辐射谱提取出的宇宙学红移，我们就能知道在特定物理时刻的宇宙红移。在观测了大量的原初黑洞群之后，我们就可以获取红移和时间的关系并用来限制宇宙的演化（示例见图9）。


图9: 通过小质量原初黑洞群构建的标准计时器

我们研究的第二种动力学系统是原初黑洞双星系统[25]。在这样的动力学系统中，标准的初始状态是关于双星系统主轴和离心率的初始概率分布。随著原初黑洞在双星系统中的运动，它们的引力效应造成了时空的扰动，从而产生了引力波。发出的引力波从原初黑洞双星中带走了能量，这改变了双星系统的主轴和离心率。这样的一种机制也改变了它们关于主轴和离心率的概率分布。所以通过研究概率分布的演化，我们可以提取出从初始状态到后期状态的物理演化时间。在引力波从原初黑洞双星传递到我们的过程中，宇宙膨胀伸拉了引力波的波长，并且在观测到的引力波中留下了宇宙红移。在引力波中的红移也导致了观测到的概率分布的坐标移动。所以通过比较观测到的概率分布和初始的标准概率分布，我们就可以获得宇宙红移。而宇宙红移和物理演化时间的关系也因此被标定。在观测到大量的来自原初黑洞双星的引力波后，从早期宇宙到现在的不同物理时刻的宇宙红移都将被标定，这也进一步告诉我们宇宙红移和标度因子是如何演化的（示例见图10）。


图10: 通过原初黑洞双星构建的标准计时器

在上述的讨论中，我们主要在原初黑洞系统中构建标准计时器。事实上，宇宙中有许多动力学系统可作为标准计时器的候选者。如果一个宇宙动力学系统具备初始状态，并且有著确切的演化机制，那么动力学系统中的物理演化时间就可以视为宇宙时间的独立测量。与此同时，宇宙膨胀也将宇宙红移留在了可观测量中。通过研究此类宇宙动力学系统，就可以获得宇宙红移和物理时间的关系，就像在宇宙中工作的标准计时器一样。例如第一代恒星，如果我们知道它们的初始质量函数和恒星形成率，通过研究它们的数量演化，我们可以构建出一种新的晚期宇宙测量标准计时器。

有著标准烛光、标准尺子、标准汽笛和标准计时器这些测量技术的帮助，宇宙的奥秘将会被揭开，而人类作为一个整体也终将理解我们所生活的这个宇宙。

参考资料︰


  1. Einstein, Albert. "Cosmological considerations on the general theory of relativity." Sitzungsber.Preuss.Akad.Wiss.Berlin (Math.Phys.),(1917): 142-152.
  2. Friedmann, Alexander. "Über die krümmung des raumes." Zeitschrift für Physik 10.1 (1922): 377-386.
  3. Friedmann, Alexander. "Über die Möglichkeiteiner Welt mitkonstanternegativerKrümmung des Raumes." Zeitschrift für Physik 21.1 (1924): 326-332.
  4. Lemaître, Georges. "Un Univershomogène de masse constante et de rayon croissant rendantcompte de la vitesse radiale des nébuleuses extra-galactiques." Annales de la Société scientifique de Bruxelles. Vol. 47. 1927.
  5. Hubble, Edwin. "A relation between distance and radial velocity among extra-galactic nebulae." Proceedings of the national academy of sciences 15.3 (1929): 168-173. [6]. Gamow, George. "Expanding universe and the origin of elements." Physical review 70.7-8 (1946): 572.
  6. Alpher, Ralph A., Hans Bethe, and George Gamow. "The origin of chemical elements." Physical Review 73.7 (1948): 803.
  7. Penzias, Arno A., and Robert Woodrow Wilson. "A measurement of excess antenna temperature at 4080 Mc/s." The Astrophysical Journal 142 (1965): 419-421.
  8. Akrami, Yashar, et al. "Planck 2018 results-IV. Diffuse component separation." Astronomy & Astrophysics 641 (2020): A4.
  9. Freeman, Kenneth C. "On the disks of spiral and S0 galaxies." The Astrophysical Journal 160 (1970): 811.
  10. Rubin, Vera C., and W. Kent Ford Jr. "Rotation of the Andromeda nebula from a spectroscopic survey of emission regions." The Astrophysical Journal 159 (1970): 379.
  11. Riess, Adam G., et al. "Observational evidence from supernovae for an accelerating universe and a cosmological constant." The Astronomical Journal 116.3 (1998): 1009.
  12. Aghanim, Nabila, et al. "Planck 2018 results-VI. Cosmological parameters." Astronomy & Astrophysics 641 (2020): A6.
  13. Leavitt, Henrietta S. "1777 variables in the Magellanic Clouds." Annals of Harvard College Observatory 60 (1908): 87-108.
  14. Leavitt, Henrietta S., and Edward C. Pickering. "Periods of 25 Variable Stars in the Small Magellanic Cloud." Harvard College Observatory Circular 173 (1912): 1-3.
  15. Baade, Walter, and Fritz Zwicky. "On super-novae." Proceedings of the National Academy of Sciences 20.5 (1934): 254-259.
  16. Abbott, Benjamin P., et al. "Observation of gravitational waves from a binary black hole merger." Physical review letters 116.6 (2016): 061102.
  17. Abbott, B. P., et al. "Multi-messenger Observations of a Binary Neutron Star Merger." The Astrophysical Journal 848.2 (2017).
  18. Riess, Adam G. "The expansion of the Universe is faster than expected." Nature Reviews Physics 2.1 (2020): 10-12.
  19. Abdalla, Elcio, et al. "Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies." Journal of High Energy Astrophysics (2022).
  20. Carr, Bernard J., and Stephen W. Hawking. "Black holes in the early Universe." Monthly Notices of the Royal Astronomical Society 168.2 (1974): 399-415.
  21. Hawking, Stephen W. "Black hole explosions?." Nature 248.5443 (1974): 30-31.
  22. Hawking, Stephen W. "Particle creation by black holes." Euclidean quantum gravity. 1975. 167-188.
  23. Cai, Yi-Fu, et al. "Cosmological Standard Timers from Unstable Primordial Relics."arXiv:2112.10422 (2021).
  24. Ding, Qianhang. "Cosmological Standard Timers from Primordial Black Hole Binaries." arXiv:2206.03142 (2022).

作者︰
香港科技大学物理系博士候选人丁干航先生
2023年1月