怎樣穿鞋帶才是最佳方法?
這不算是個數學問題,所以讓我們換個問法:怎樣能用最少的鞋帶,以及怎樣能最穩妥地把鞋帶穿好?
相信你從來都不用擔心這些問題,但也許你的父母還記得以前剪下鞋帶來穿,然後確定鞋帶是否穿得穩妥的日子,在這種情況下就顯出這些問題的重要性了;現在我們之所以不用操心是因為製造商在銷售前就已經穿好鞋帶,而他們的成本和利潤全都取決於這些問題,他們或許也使用與本文相同的數學角度作出選擇。
關於穿鞋帶
從數學角度看,一隻鞋有兩行孔眼,每行各有n個孔眼,我們可以把A行和B行的孔眼以A1到An,及B1到Bn表示(見圖一)。在不失一般性的情況下,設A、B行之間的間隙為g單位,同一行上下孔眼之間的高度則為h單位。由一個孔眼到另一個孔眼之間的一段鞋帶被稱為一個線段;而一個綁法是指把鞋帶由An穿起,中間穿過每個孔眼一次,最後穿過Bn作結。透過簡單數算,我們知道一個完整綁法裡會有2n – 1個線段。
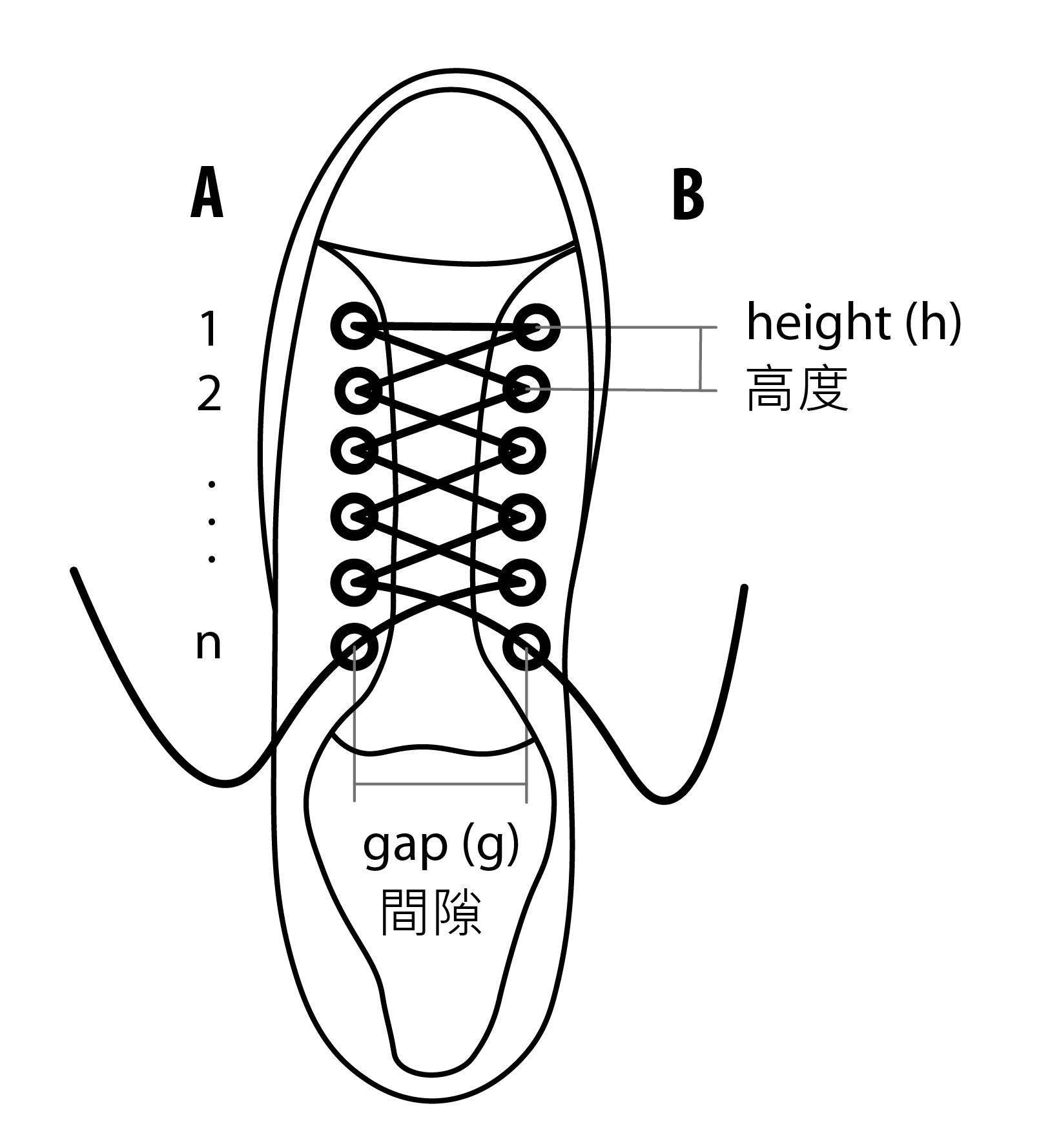
圖一:以由2n – 1個線段組成的綁法穿好的鞋
由於穿鞋帶的主要目的是把鞋的左右兩邊拉在一起,因此我們可以加一條規則,訂明鞋帶不能連續穿過三個或以上同一行的孔眼[1],換言之即是我們不能在同一行穿一條長直線。
「緊密」綁法還有多一個額外條件,就是鞋帶必須在A、B行之間交錯,不能包含垂直線段。圖二顯示三種最常見的緊密綁法,分別是交叉綁法(crisscross)、歐洲綁法(European)和鞋店綁法(shoe-store)[2]:
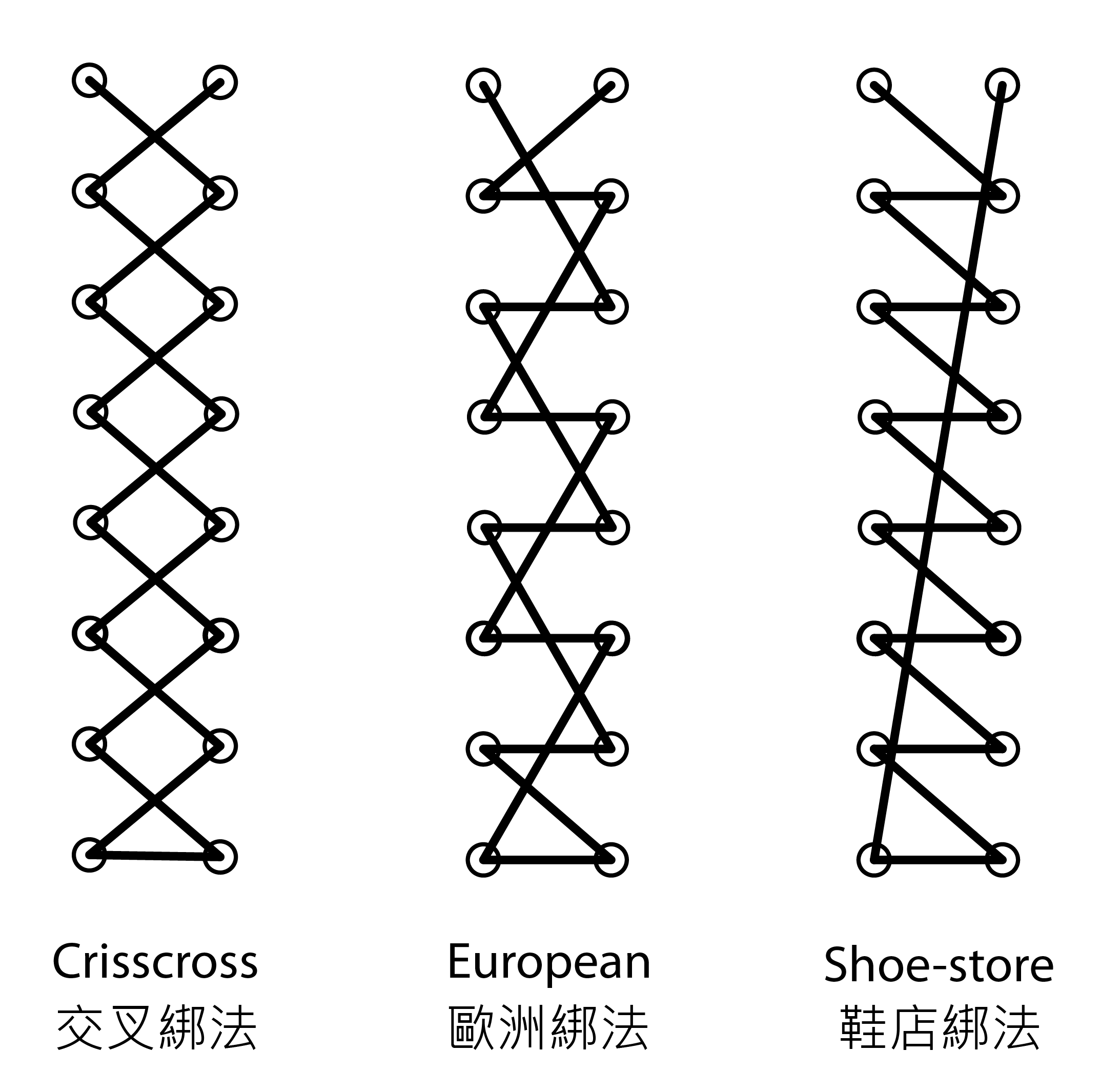
圖二:常見的緊密綁法:交叉綁法、歐洲綁法和鞋店綁法
另一方面,包含垂直線段的兩個常見綁法是加拿大五線譜綁法(Canadian straitlacing)和領結綁法(bowtie)(圖三)。(前者是傳統上加拿大軍隊使用的綁法,優點是在危急時用一刀就能把軍靴的鞋帶切開,容易把鞋脫出 [3]。)
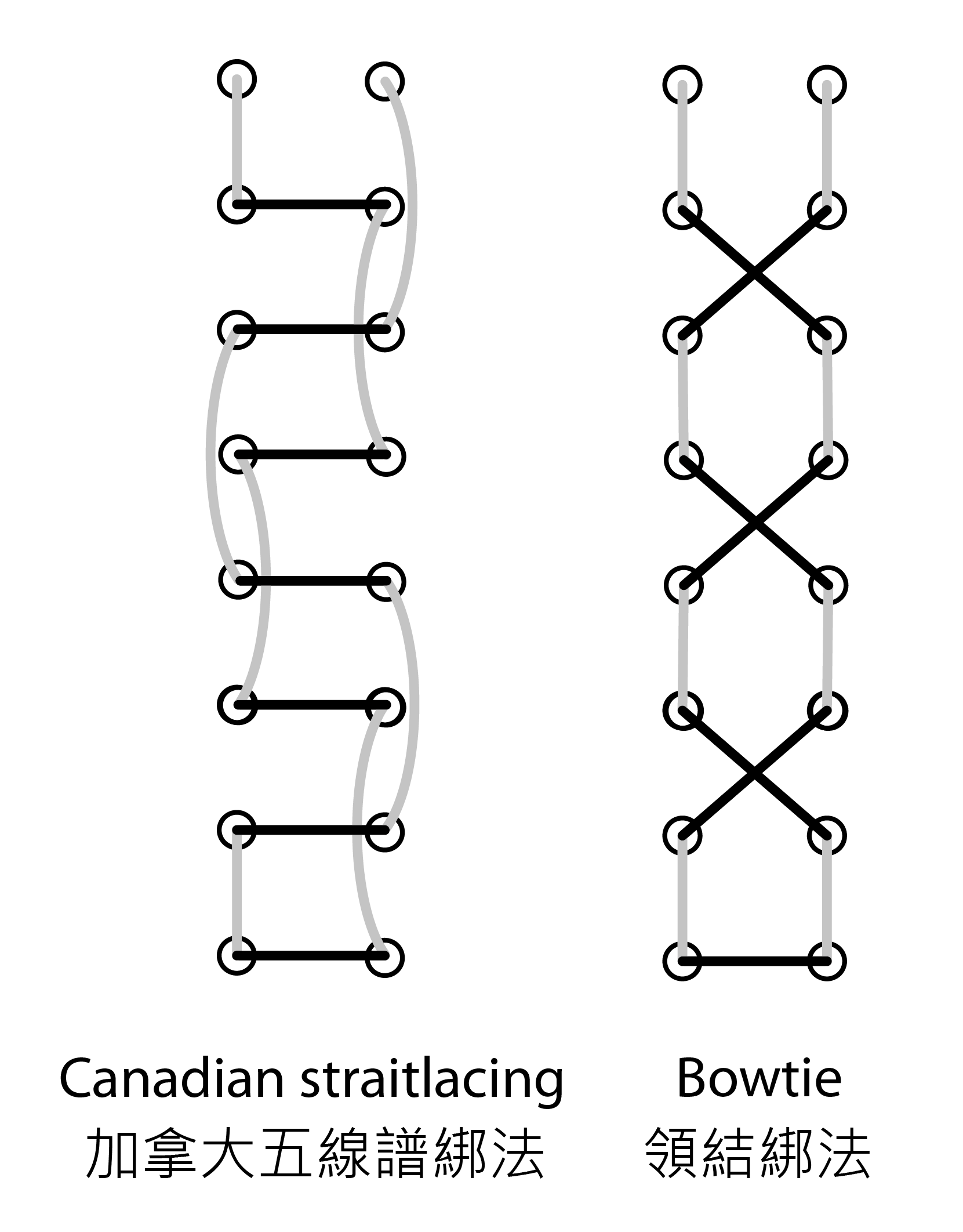
圖三:包含垂直線段的常見綁法:加拿大五線譜綁法和領結綁法。灰色線代表藏在底下的鞋帶。
最短的綁法
首先讓我們探討緊密綁法。假設鞋帶被拉緊,沒有因鬆弛而耗用多餘長度,我們就能用畢氏定理,以h、g和n表示各種綁法所需的鞋帶長度 [4],有興趣的讀者可以試試看著圖樣推導公式:
交叉綁法: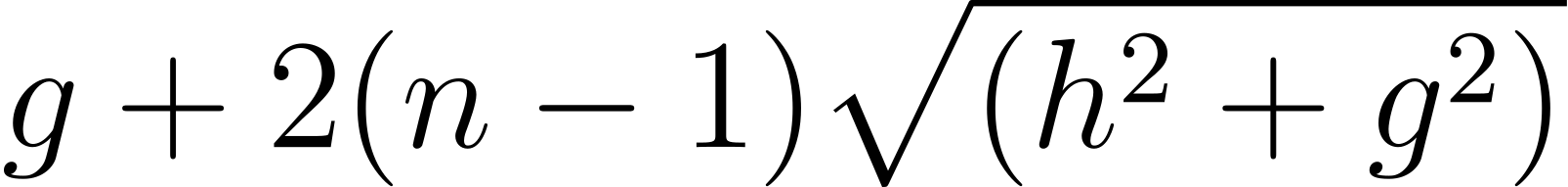
歐洲綁法: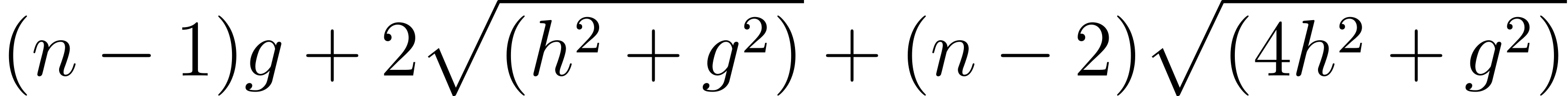
鞋店綁法: 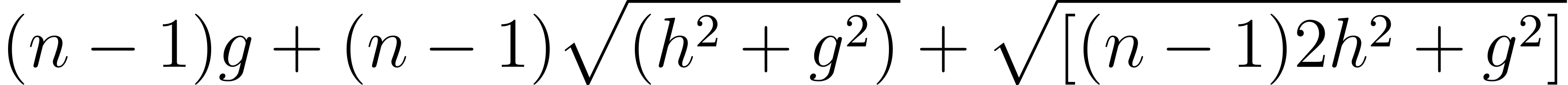
然而它們線段交錯的性質使我們不需進行計算就能比較三者長度,譬如鞋帶線段的一端位於A行的Ak孔眼,假設我們在B行設置一塊鏡把A行反射,鏡中反射的A行鏡像現在就可以被畫在圖表上,並被命名為新設的C行,而Ak的鏡像則被標示為Ck。透過繼續重覆這個步驟「解開」鞋帶[5],我們的鞋帶就不再是交錯在兩行之間,而變成逐行向橫發展的圖四,當中每個線段都反映其真實長度。
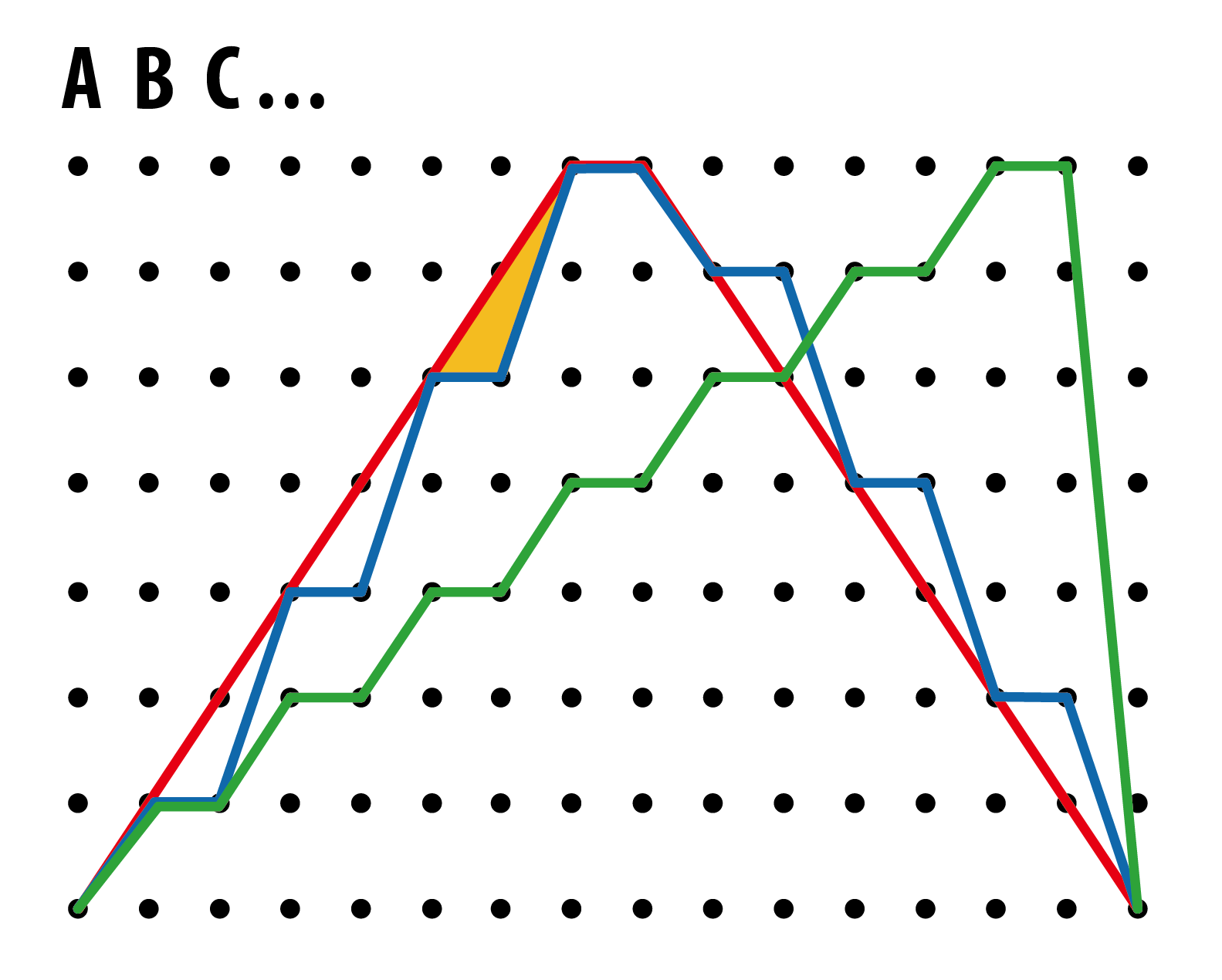
圖四:三種交錯綁法經「拆解」後的路徑圖:交叉綁法(紅色)、歐洲綁法(藍色)和鞋店綁法(綠色)[4]。橙色三角形能被用於比較交叉綁法和歐洲綁法的長度。
透過考慮圖四中的橙色三角形,我們知道以交叉綁法穿的鞋帶一定短於歐洲綁法,因為歐洲綁法的鞋帶反覆地在圖表裡構成三角形的兩條邊,而交叉綁法的鞋帶則成為餘下的第三條邊,因此根據三角不等式(三角形任何兩條邊的長度總和必定比餘下一條長),歐洲綁法比交叉綁法長。至於要比較歐洲綁法和鞋店綁法,我們可以暫時忽略水平線段(兩者同樣有n – 1個水平線段)和相同斜度的線段,把它們移除後會得到圖五(左)以深色線表示的路徑。
現在如果我們在兩個V字的尖端放一塊水平方向的鏡,以淺色表示的反射影像清楚顯示鞋店綁法的線段成了三角形的兩條邊,而歐洲綁法的線段則構成第三條邊(圖五(右))。所以再一次根據三角不等式,鞋店綁法比歐洲綁法長;而三者之中交叉綁法必為最短。事實上,交叉綁法亦已被證實是所有可行交錯綁法中最短的一款 [2]。
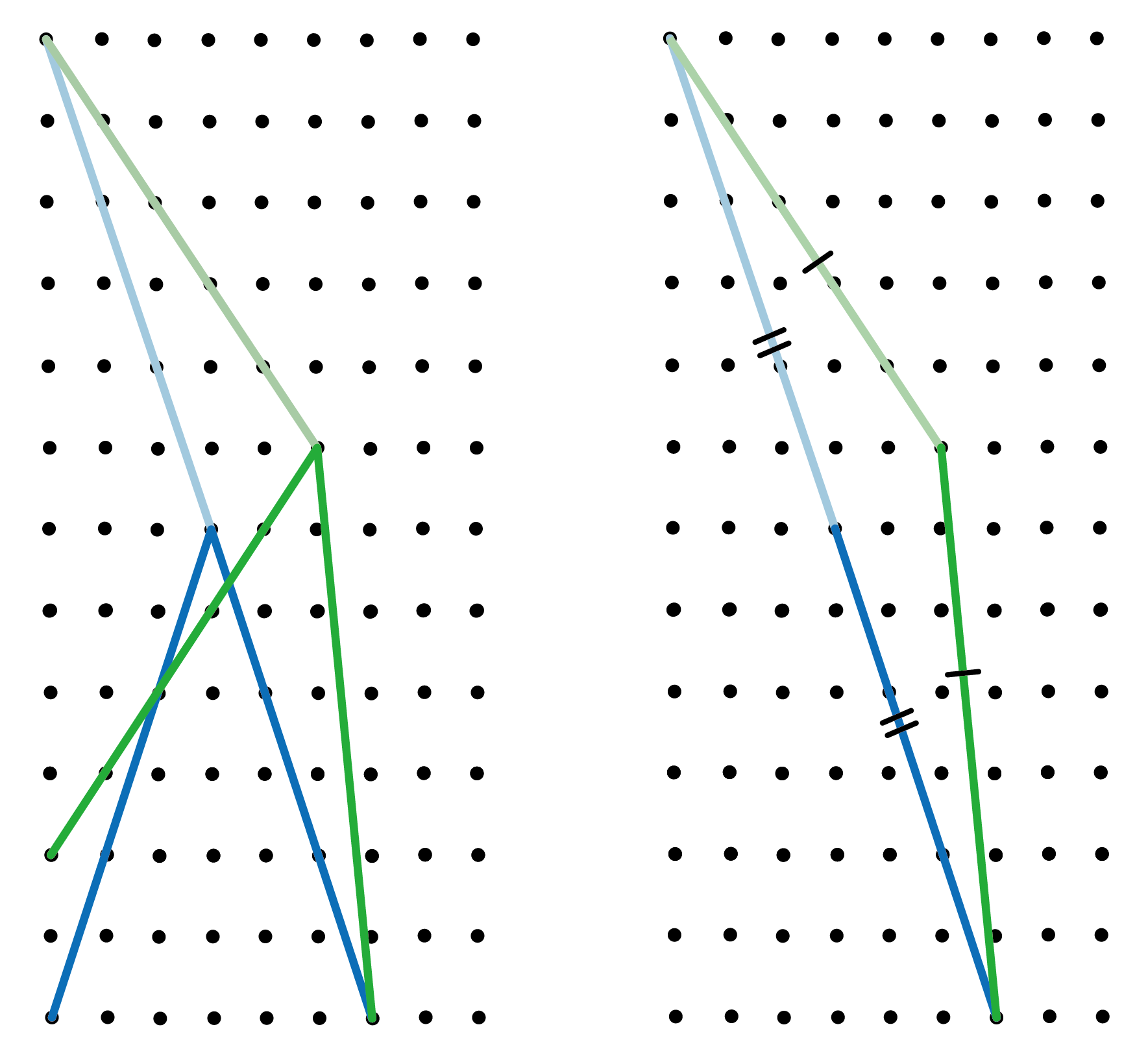
圖五:(左)減去共同線段後歐洲綁法(藍色)和鞋店綁法(綠色)經「拆解」後的路徑及其反射影像(以淺色表示)[3];(右)判斷兩者長度需考慮的三角形。
至於要找出所有綁法中最短的一款,記得穿鞋帶的目的是要把鞋的左右兩半拉在一起。打交叉是用最少鞋帶就能把鞋水平拉緊,而又能垂直地向下一行孔眼發展的方法。雖然包括加拿大五線譜綁法在內的一些綁法只用水平和垂直線段,但是這些方法都耗用極長的垂直線段,因此最短的綁法需要包含交叉。也有綁法包含由多個重疊交叉組合而成的複雜圖案,但最短的綁法明顯地只需在兩行孔眼之間打出簡單交叉,所以最短的綁法只能包含簡單交叉。然而根據三角不等式,兩條垂直線段長度之和總是短於任何交叉(見圖六),所以我們要儘可能增加垂直線段的數目,同時亦要減少簡單交叉。

圖六:簡單交叉(藍色)和兩條垂直線段(綠色)之間的長度比較。
在顧及不可連續綁出垂直線段的前提下,我們可以在交叉綁法中儘可能加入垂直線段代替部分交叉,而得出的綁法不就是領結嗎?因為只有領結綁法符合這些描述,所以它必定是最短的綁法 [6]
最穩妥的綁法
那麼,哪種才是最穩妥的綁法?當你索緊鞋帶時,孔眼和鞋帶的運作原理就像滑輪(pulley),因此問題可以改為如何打造最強的滑輪組。穿好鞋帶後,其張力為恆定的T;而我們關注的是水平張力Th,因為水平是把鞋的左右兩邊拉在一起的方向。在水平線段中,Th = T;在垂直線段中,Th = 0;在斜向線段中,Th是T的水平分量(horizontal component),數值可以藉簡單的三角函數計算。一個綁法中每個孔眼間Th的總和被稱為滑輪和(pulley sum),而最穩妥的綁法應擁有最大的滑輪和。
再進一步討論之前,讓我們設兩行孔眼之間的間隙g為1個單位。這能簡化之後的計算,因為現在同一行上下孔眼之間的高度h亦可以被想作{上下孔眼間高度}/{左右孔眼間隙}之比。
已有理論證明最穩妥的綁法為最常見的交叉綁法和鞋店綁法 [6]。為了決定在某一情況下哪種才是較穩妥的綁法,我們需考慮孔眼數目n和上下孔眼間的相對高度h。
在n > 2的情況下,設C(n, h)為交叉綁法的滑輪和,S(n, h)為鞋店綁法的滑輪和。每個孔眼數目n都有一個對應的hn > 0使C(n, hn) = S(n, hn),而:
- 當h < hn,交叉綁法最為穩妥;
- 當h = hn,兩種綁法同樣穩妥;
- 當h > hn,鞋店綁法最為穩妥。
換言之,當孔眼上下高度比較接近,最穩妥的會是交叉綁法;上下高度比較遠時,最穩妥的則會是鞋店綁法。
對於數值較小的n,hn的近似值可見於下表 [6]:
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| hn | 0.9029 | 0.7412 | 0.6450 | 0.5794 | 0.5309 | 0.4931 | 0.4625 | 0.4372 |
你可以自行量度鞋上高度間隙之比找出相對高度h,再透過比對孔眼數目n,在表上找出hn的相應值。筆者寫這篇文章時穿著以交叉綁法穿的鞋,鞋子有4對孔眼,而h值約為0.4,所以我在穿鞋帶時顯然做了正確的決定。當然,現在鞋店裡售賣的鞋都用上h值非常接近hn的設計,所以無論你選擇哪款綁法都會非常穩妥 [6]。
所以我們應該怎樣穿鞋帶呢?這視乎你想選擇使用更少鞋帶的綁法,還是採取更穩妥的方法。如果要在最短的長度和最大的穩妥程度之間取個平衡,交叉綁法似乎是個最佳選擇,所以在沒有數值在手的情況下你應該選擇這種綁法;雖然領結綁法也能給你可接受的穩妥程度,它至少不會使你的鞋子分開兩截。然而這些數值其實也近在手邊,只要你有尺子、網絡(或《科言》實體書)和追根究底的「八卦」天性就足夠;最後一樣尤其重要,有了它,你就幾乎能解決任何迎面而來的問題。
參考資料:
- Polster, B. (2002). What is the best way to lace your shoes? Nature, 420, 476. https://doi.org/10.1038/420476a
- Stewart, I. (1996). Arithmetic and old lace. Scientific American, 275(1), 94-97. https://www.jstor.org/stable/24993276
- Stewart, I. (2006). How to Cut a Cake and Other Mathematical Conundrums. Oxford University Press.
- Peterson, I. (2020, October 30). The Shoelace Problem. The Mathematical Tourist. http://mathtourist.blogspot.com/2020/10/the-shoelace-problem.html.
- Halton, J. H. (1992). The shoelace problem (No. 92-032). Department of Computer Science, UNC Chapel Hill.
- Polster, B. (2006). The Shoelace Book: A Mathematical Guide to the Best (and Worst) Ways to Lace Your Shoes. American Mathematical Society.
作者︰
香港科技大學《科言》學生編輯 胡適之
譯者:
香港科技大學《科言》總編輯 劉劭行
2024年6月

