怎样穿鞋带才是最佳方法?
这不算是个数学问题,所以让我们换个问法:怎样能用最少的鞋带,以及怎样能最稳妥地把鞋带穿好?
相信你从来都不用担心这些问题,但也许你的父母还记得以前剪下鞋带来穿,然后确定鞋带是否穿得稳妥的日子,在这种情况下就显出这些问题的重要性了;现在我们之所以不用操心是因为制造商在销售前就已经穿好鞋带,而他们的成本和利润全都取决于这些问题,他们或许也使用与本文相同的数学角度作出选择。
关于穿鞋带
从数学角度看,一只鞋有两行孔眼,每行各有n个孔眼,我们可以把A行和B行的孔眼以A1到An,及B1到Bn表示(见图一)。在不失一般性的情况下,设A、B行之间的间隙为g单位,同一行上下孔眼之间的高度则为h单位。由一个孔眼到另一个孔眼之间的一段鞋带被称为一个线段;而一个绑法是指把鞋带由An穿起,中间穿过每个孔眼一次,最后穿过Bn作结。透过简单数算,我们知道一个完整绑法里会有2n – 1个线段。
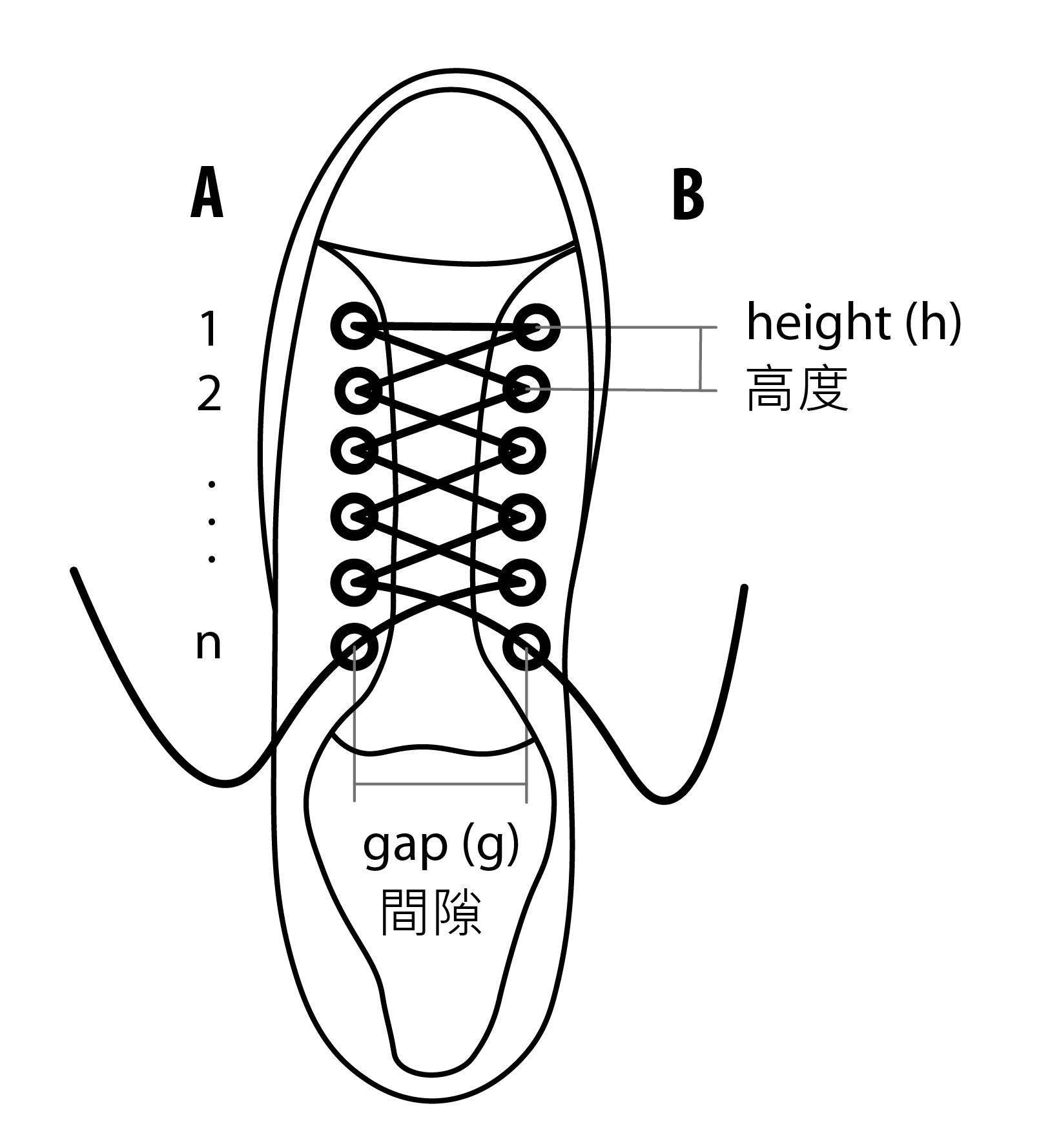
图一:以由2n – 1个线段组成的绑法穿好的鞋
由于穿鞋带的主要目的是把鞋的左右两边拉在一起,因此我们可以加一条规则,订明鞋带不能连续穿过三个或以上同一行的孔眼[1],换言之即是我们不能在同一行穿一条长直线。
「紧密」绑法还有多一个额外条件,就是鞋带必须在A、B行之间交错,不能包含垂直线段。图二显示三种最常见的紧密绑法,分别是交叉绑法(crisscross)、欧洲绑法(European)和鞋店绑法(shoe-store)[2]:
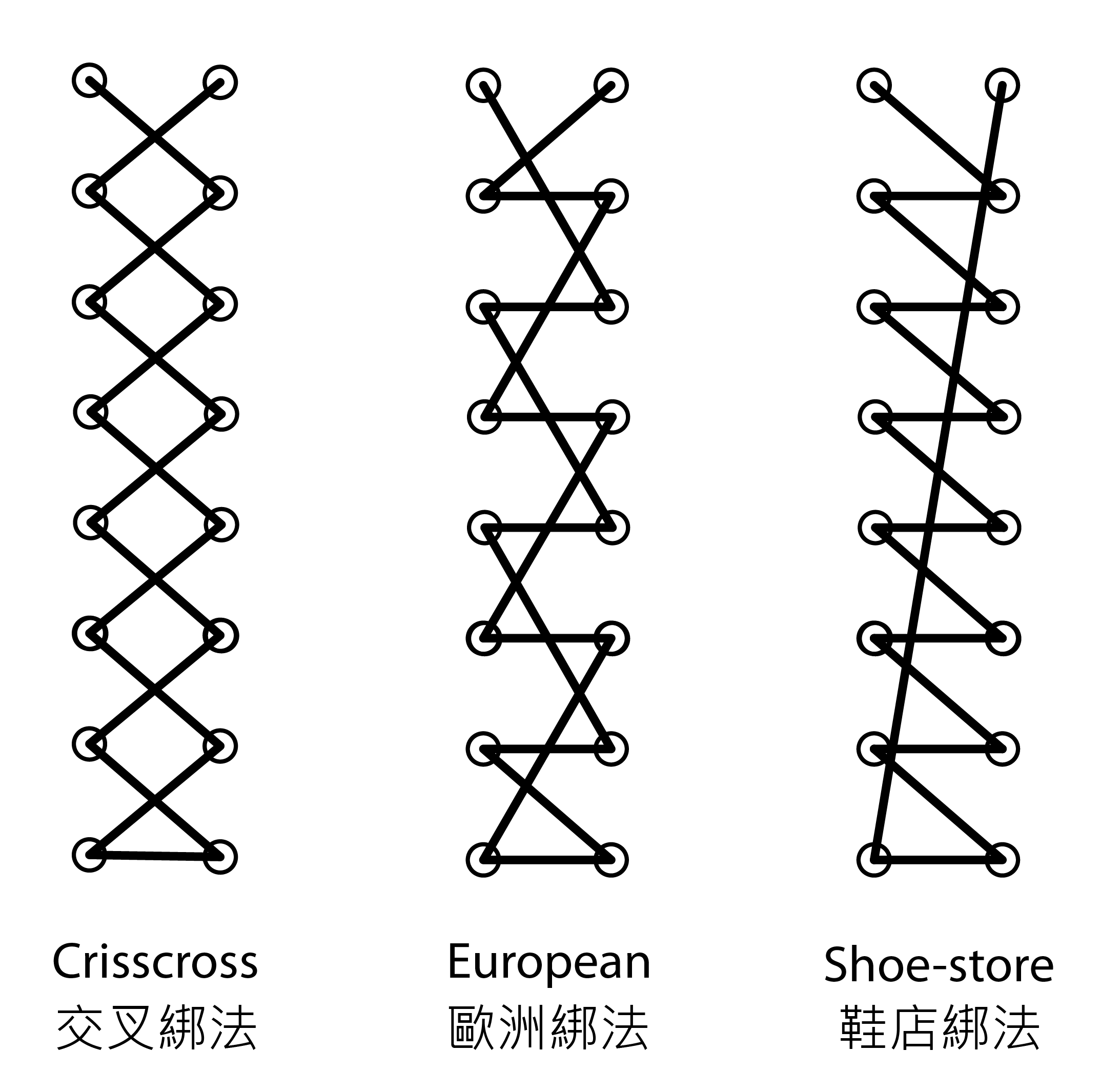
图二:常见的紧密绑法:交叉绑法、欧洲绑法和鞋店绑法
另一方面,包含垂直线段的两个常见绑法是加拿大五线谱绑法(Canadian straitlacing)和领结绑法(bowtie)(图三)。(前者是传统上加拿大军队使用的绑法,优点是在危急时用一刀就能把军靴的鞋带切开,容易把鞋脱出 [3]。)
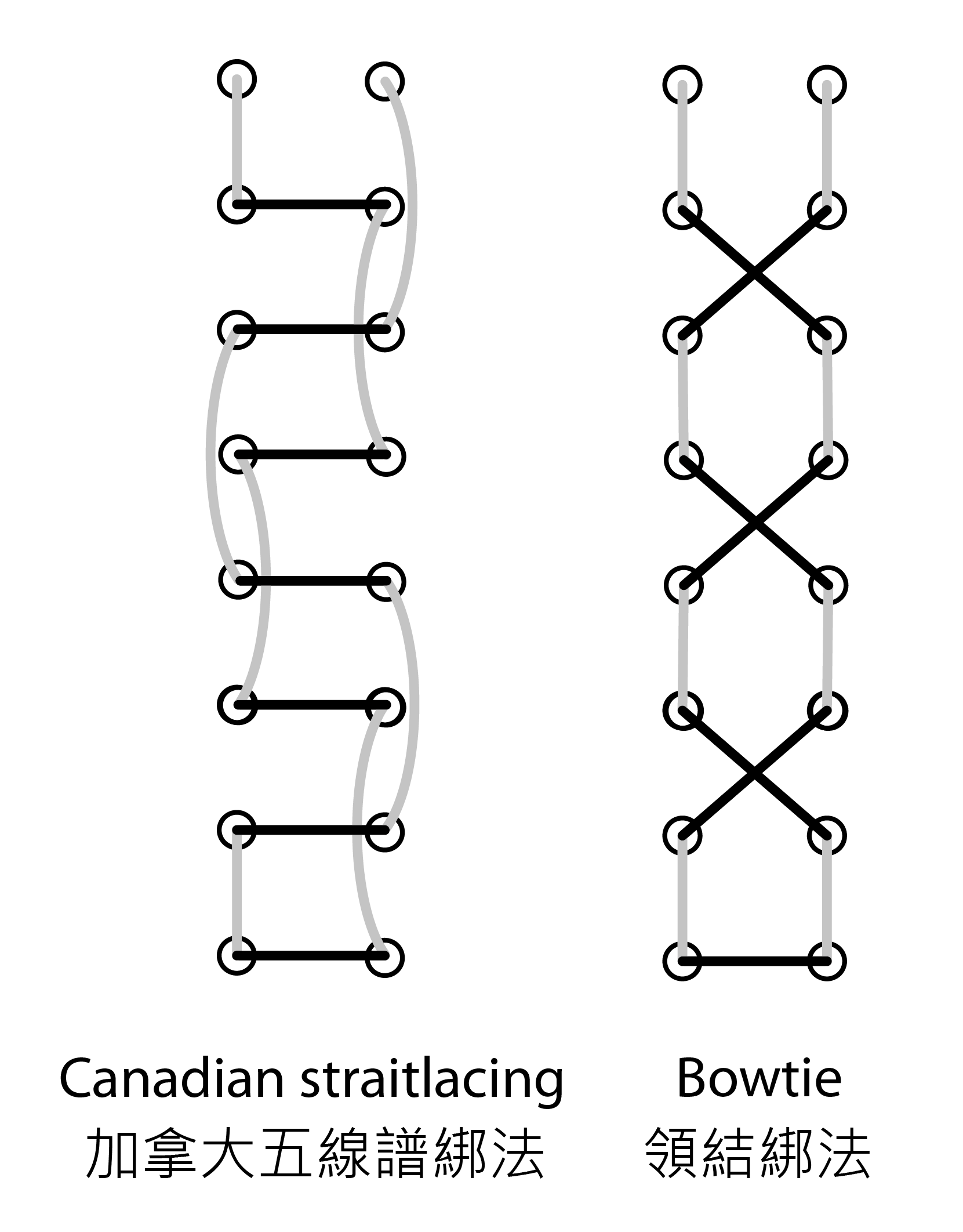
图三:包含垂直线段的常见绑法:加拿大五线谱绑法和领结绑法。灰色线代表藏在底下的鞋带。
最短的绑法
首先让我们探讨紧密绑法。假设鞋带被拉紧,没有因松弛而耗用多余长度,我们就能用毕氏定理,以h、g和n表示各种绑法所需的鞋带长度 [4],有兴趣的读者可以试试看著图样推导公式:
交叉绑法: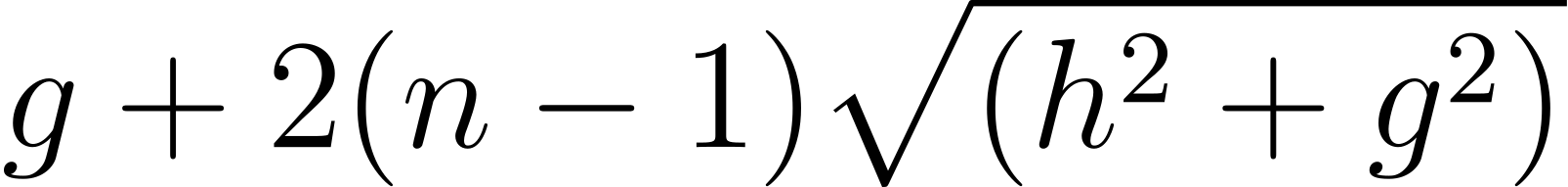
欧洲绑法: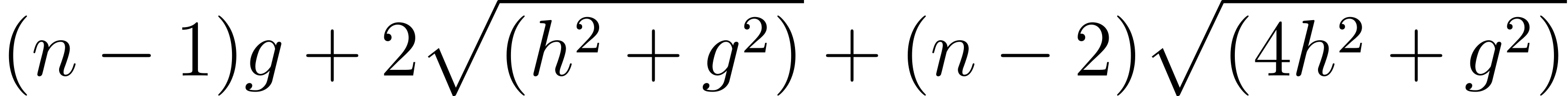
鞋店绑法: 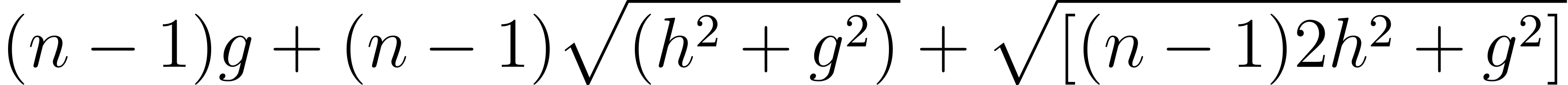
然而它们线段交错的性质使我们不需进行计算就能比较三者长度,譬如鞋带线段的一端位于A行的Ak孔眼,假设我们在B行设置一块镜把A行反射,镜中反射的A行镜像现在就可以被画在图表上,并被命名为新设的C行,而Ak的镜像则被标示为Ck。透过继续重复这个步骤「解开」鞋带[5],我们的鞋带就不再是交错在两行之间,而变成逐行向横发展的图四,当中每个线段都反映其真实长度。
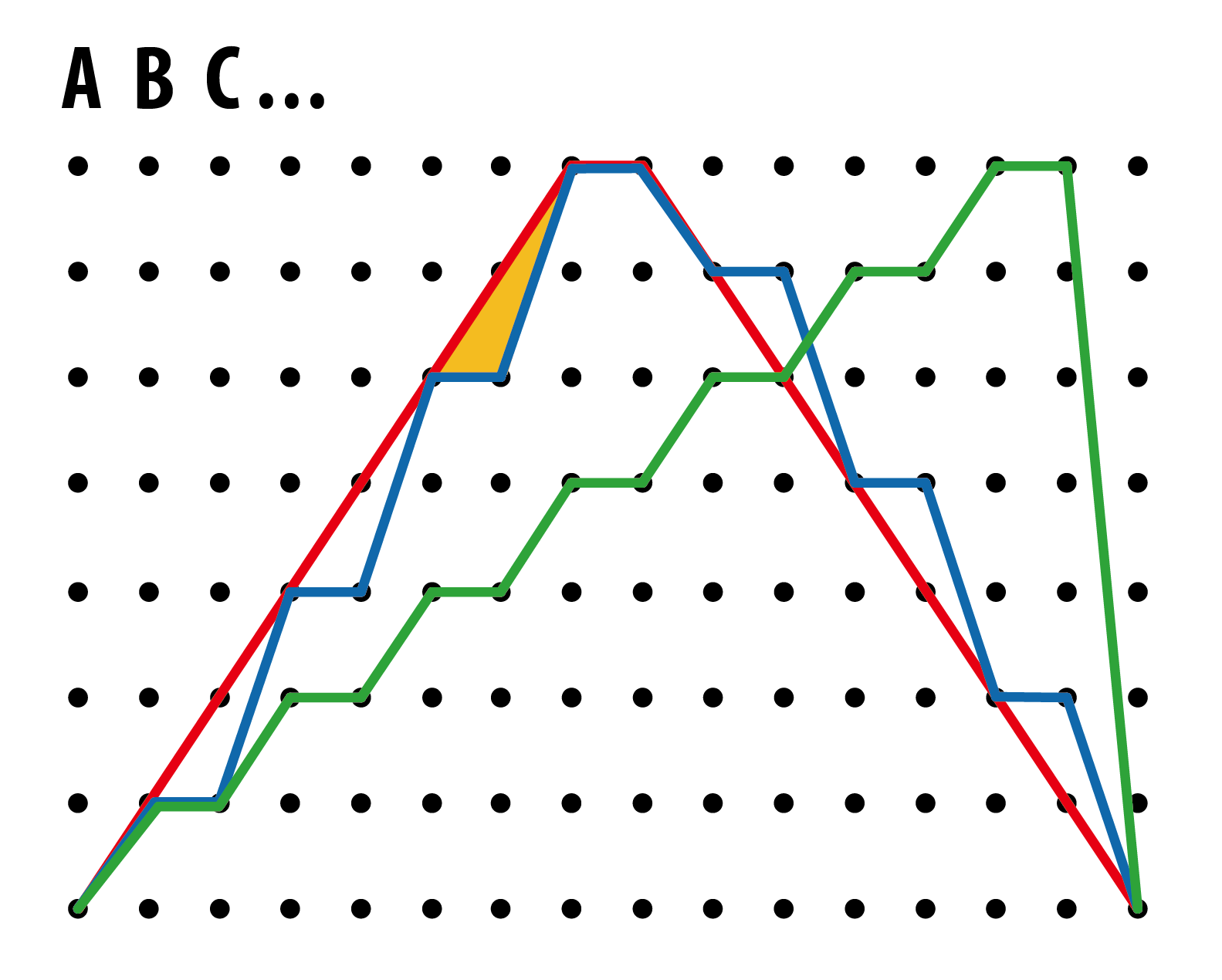
图四:三种交错绑法经「拆解」后的路径图:交叉绑法(红色)、欧洲绑法(蓝色)和鞋店绑法(绿色)[4]。橙色三角形能被用于比较交叉绑法和欧洲绑法的长度。
透过考虑图四中的橙色三角形,我们知道以交叉绑法穿的鞋带一定短于欧洲绑法,因为欧洲绑法的鞋带反复地在图表里构成三角形的两条边,而交叉绑法的鞋带则成为余下的第三条边,因此根据三角不等式(三角形任何两条边的长度总和必定比余下一条长),欧洲绑法比交叉绑法长。至于要比较欧洲绑法和鞋店绑法,我们可以暂时忽略水平线段(两者同样有n – 1个水平线段)和相同斜度的线段,把它们移除后会得到图五(左)以深色线表示的路径。
现在如果我们在两个V字的尖端放一块水平方向的镜,以浅色表示的反射影像清楚显示鞋店绑法的线段成了三角形的两条边,而欧洲绑法的线段则构成第三条边(图五(右))。所以再一次根据三角不等式,鞋店绑法比欧洲绑法长;而三者之中交叉绑法必为最短。事实上,交叉绑法亦已被证实是所有可行交错绑法中最短的一款 [2]。
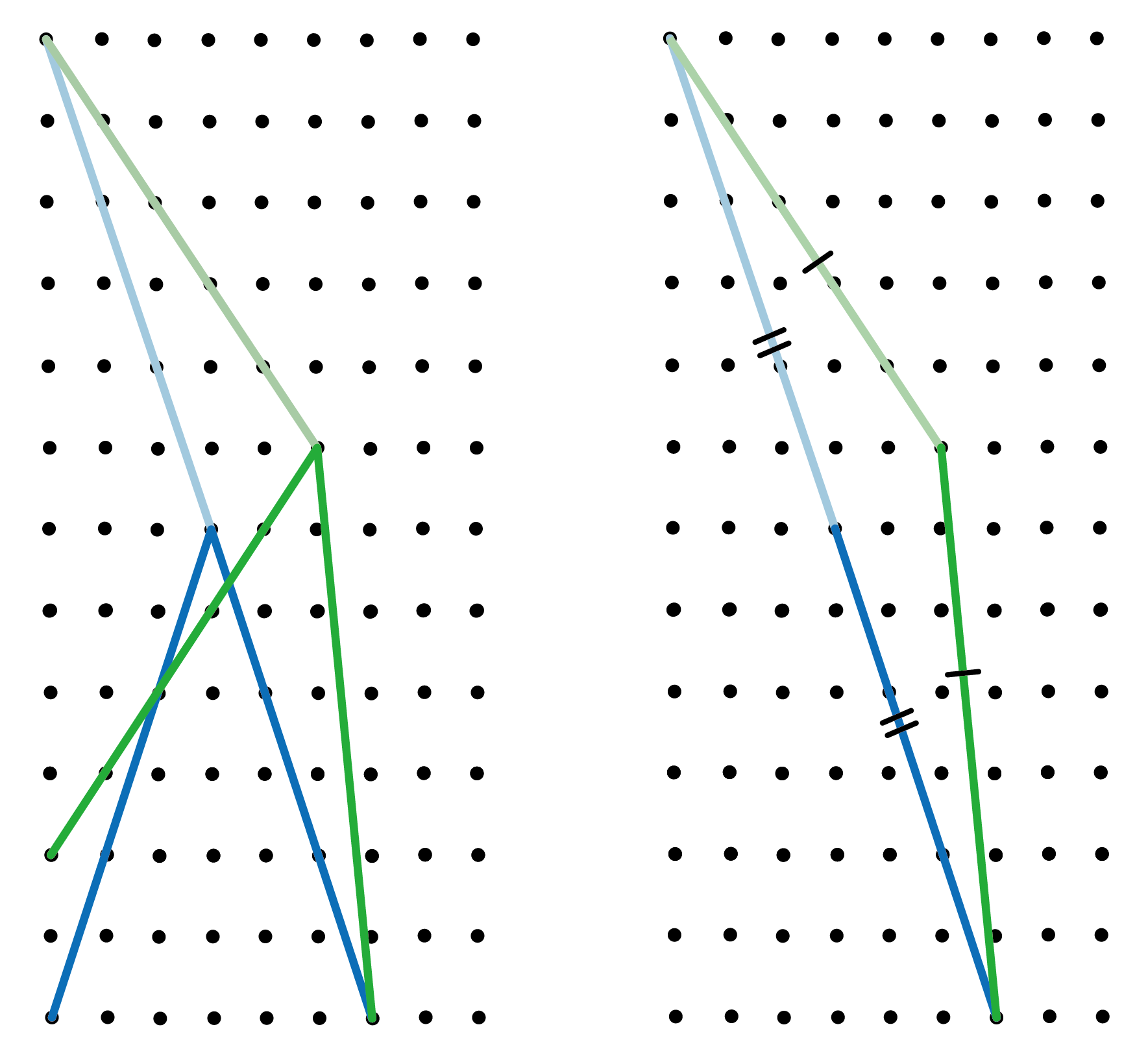
图五:(左)减去共同线段后欧洲绑法(蓝色)和鞋店绑法(绿色)经「拆解」后的路径及其反射影像(以浅色表示)[3];(右)判断两者长度需考虑的三角形。
至于要找出所有绑法中最短的一款,记得穿鞋带的目的是要把鞋的左右两半拉在一起。打交叉是用最少鞋带就能把鞋水平拉紧,而又能垂直地向下一行孔眼发展的方法。虽然包括加拿大五线谱绑法在内的一些绑法只用水平和垂直线段,但是这些方法都耗用极长的垂直线段,因此最短的绑法需要包含交叉。也有绑法包含由多个重叠交叉组合而成的复杂图案,但最短的绑法明显地只需在两行孔眼之间打出简单交叉,所以最短的绑法只能包含简单交叉。然而根据三角不等式,两条垂直线段长度之和总是短于任何交叉(见图六),所以我们要尽可能增加垂直线段的数目,同时亦要减少简单交叉。

图六:简单交叉(蓝色)和两条垂直线段(绿色)之间的长度比较。
在顾及不可连续绑出垂直线段的前提下,我们可以在交叉绑法中尽可能加入垂直线段代替部分交叉,而得出的绑法不就是领结吗?因为只有领结绑法符合这些描述,所以它必定是最短的绑法 [6]
最稳妥的绑法
那么,哪种才是最稳妥的绑法?当你索紧鞋带时,孔眼和鞋带的运作原理就像滑轮(pulley),因此问题可以改为如何打造最强的滑轮组。穿好鞋带后,其张力为恒定的T;而我们关注的是水平张力Th,因为水平是把鞋的左右两边拉在一起的方向。在水平线段中,Th = T;在垂直线段中,Th = 0;在斜向线段中,Th是T的水平分量(horizontal component),数值可以藉简单的三角函数计算。一个绑法中每个孔眼间Th的总和被称为滑轮和(pulley sum),而最稳妥的绑法应拥有最大的滑轮和。
再进一步讨论之前,让我们设两行孔眼之间的间隙g为1个单位。这能简化之后的计算,因为现在同一行上下孔眼之间的高度h亦可以被想作{上下孔眼间高度}/{左右孔眼间隙}之比。
已有理论证明最稳妥的绑法为最常见的交叉绑法和鞋店绑法 [6]。为了决定在某一情况下哪种才是较稳妥的绑法,我们需考虑孔眼数目n和上下孔眼间的相对高度h。
在n > 2的情况下,设C(n, h)为交叉绑法的滑轮和,S(n, h)为鞋店绑法的滑轮和。每个孔眼数目n都有一个对应的hn > 0使C(n, hn) = S(n, hn),而:
- 当h < hn,交叉绑法最为稳妥;
- 当h = hn,两种绑法同样稳妥;
- 当h > hn,鞋店绑法最为稳妥。
换言之,当孔眼上下高度比较接近,最稳妥的会是交叉绑法;上下高度比较远时,最稳妥的则会是鞋店绑法。
对于数值较小的n,hn的近似值可见于下表 [6]:
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| hn | 0.9029 | 0.7412 | 0.6450 | 0.5794 | 0.5309 | 0.4931 | 0.4625 | 0.4372 |
你可以自行量度鞋上高度间隙之比找出相对高度h,再透过比对孔眼数目n,在表上找出hn的相应值。笔者写这篇文章时穿著以交叉绑法穿的鞋,鞋子有4对孔眼,而h值约为0.4,所以我在穿鞋带时显然做了正确的决定。当然,现在鞋店里售卖的鞋都用上h值非常接近hn的设计,所以无论你选择哪款绑法都会非常稳妥 [6]。
所以我们应该怎样穿鞋带呢?这视乎你想选择使用更少鞋带的绑法,还是采取更稳妥的方法。如果要在最短的长度和最大的稳妥程度之间取个平衡,交叉绑法似乎是个最佳选择,所以在没有数值在手的情况下你应该选择这种绑法;虽然领结绑法也能给你可接受的稳妥程度,它至少不会使你的鞋子分开两截。然而这些数值其实也近在手边,只要你有尺子、网络(或《科言》实体书)和追根究底的「八卦」天性就足够;最后一样尤其重要,有了它,你就几乎能解决任何迎面而来的问题。
参考资料:
- Polster, B. (2002). What is the best way to lace your shoes? Nature, 420, 476. https://doi.org/10.1038/420476a
- Stewart, I. (1996). Arithmetic and old lace. Scientific American, 275(1), 94-97. https://www.jstor.org/stable/24993276
- Stewart, I. (2006). How to Cut a Cake and Other Mathematical Conundrums. Oxford University Press.
- Peterson, I. (2020, October 30). The Shoelace Problem. The Mathematical Tourist. http://mathtourist.blogspot.com/2020/10/the-shoelace-problem.html.
- Halton, J. H. (1992). The shoelace problem (No. 92-032). Department of Computer Science, UNC Chapel Hill.
- Polster, B. (2006). The Shoelace Book: A Mathematical Guide to the Best (and Worst) Ways to Lace Your Shoes. American Mathematical Society.
作者︰
香港科技大学《科言》学生编辑 胡适之
译者:
香港科技大学《科言》总编辑 刘劭行
2024年6月

