極小曲面是微分幾何學裏最重要的研究對象之一。極小曲面除了本身富有數學美之外,在諸多物理現象中亦會自然出現,例如相變(phase transition)[1] 以及蝴蝶翅 膀鱗片的生物光子納米結構[2](圖1)。極小曲面在材料科學、工程學,甚至藝術、建築領域均佔有席位。Frei Otto 亦在幾項建築作品的設計中運用了極小曲面,包括1972年德國慕尼黑奧林匹克運動場(圖2)。

圖1 - 蝴蝶翅膀鱗片中的螺旋二十四面體(gyroid)結構(資料來源:[2])

圖2 -位於慕尼克北部的慕尼黑奧林匹克公園正中心的奧林匹克運動場,乃1972年夏季奧運會的主要會場(資料來源: https://munich-info.info/olympic_stadium_munich/)
肥皂膜及普拉托的實驗 事實上,要窺探何謂極小曲面,並不需要有科學家或建築師的知識水平,因為這類曲面其實我們自小就見過,就是肥皂膜以及其類似的形態 - 肥皂泡。如果將一條金屬圈浸入皂液再取出,就會看到線的邊緣拉出一層薄肥皂膜。例如,用圓形線圈可以拉 出一隻平碟。如果用兩個平行同軸圓形線圈,就會拉出一個旋轉對稱肥皂膜,這種型狀叫作懸鏈曲面(catenoid)(圖3)。在十九世紀 ,比利時物理學家兼數學家約瑟夫.普拉托(Joseph Plateau)是首位利用不同形狀金屬線做實驗、大規模研究肥皂膜的學者。他從實驗的觀察結果總結出一套名為「普拉托定律」的法則,用以描述一切有可能形成的肥皂膜之形狀及特性(圖4)。

圖3 - 平碟形(左)及懸鏈曲面(右)肥皂膜(資料來源:http://soft-matter.seas.harvard.edu/index.php/Soap_films)

圖4 - 肥皂膜所呈現的普拉托定律 (資料來源:“The Geometry of Soap Films and Soap Bubbles”《肥皂膜及肥皂泡的幾何學》, F Almgren and J Taylor, Scientific American (1976))
肥皂膜所蘊含的數學 普拉托的實驗靈感源自Joseph-Louis Lagrange於1760年提出的一個數學問題——給定固定邊界後,是否總是存在面積達至最小的曲面?決定肥皂膜形狀的根本機制是建基於一條原則 - 盡可能達致最少物理能量(在理想情況下,大致就是曲面的面積)。這項聽來簡單的構念名為「最小作用量原理」(least action principle),可以用來在多種情況下衍生出許多物理定律,包括楊米理論(Yang-Mills theory)、愛因斯坦的廣義相對論。雖然普拉托的實驗為肥皂膜建立了一套完備的模型,但後來學者發現難以用嚴格的數學語言來證明該等肥皂膜曲面的存在。直至1930年,這項難題終於由Jesse Douglas及Tibor Radó各自分別解決,這是極重大的突破!這項成就之突出,使Douglas在1936年獲頒第一個有「諾貝爾數學獎」之稱的費爾茲獎章。約四十年後,Jean Taylor[3]發表《普拉托定律》的第一套數學證明,從而驗證了普拉托在一個多世紀前從肥皂膜實驗所得到的觀察結果。
Jean Taylor在證明其著名理論時所用的技巧,與Douglas及Radó在解決普拉托問題時所用的不同。他的構思是屬於數學裏的一個研究領域,名為「幾何測度論」(Geometric Measure Theory,GMT),在研究幾何變分問題(geometric variational problems)所產生的物體(如肥皂膜及肥皂泡)之一般形狀及精細結構方面,是極之有用的工具。
在一窺GMT所涉的內容之前,我們先仔細定義「曲面」為何物。在數學裏,曲面是個看起來像小型彈性膜的二維空間。在一個曲面裏,如果每個點都有明確的「切平面」(tangent plane)(換言之無任何利邊或角),這個曲面就可算是「平滑」。GMT的一項重要技巧是爆發過程(blow-up process)。簡單而言,如果想要瞭解曲面某個點周圍的精細局部結構,可以假想用顯微鏡放大該點周圍的區域。當不斷增加顯微鏡的放大率時,曲面的某個平滑點看起來就會越來越像平面。相反,如果將一個奇點(singular point)放大(例如肥皂膜的邊緣或頂點),就會看到一些與平面不同的極限幾何形狀。透過研究從這些爆發過程可以得到的極限形狀,我們可以推斷出奇點周圍的局部結構(圖5)。這項構思遠遠超過極小曲面的範疇,但對研究晶界運動(grain boundary motion)[4]及融冰介面[5]中出現的奇點至關重要。
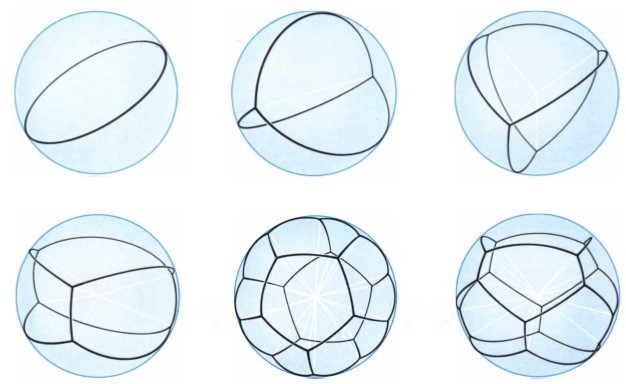
圖5 - 在爆發過程中可能出現的一些極限幾何形狀(資料來源:“The Geometry of Soap Films and Soap Bubbles”《肥皂膜及肥皂泡的幾何學》, F Almgren and J Taylor, Scientific American (1976))
有關極小曲面的一個自由邊界問題 普拉托的問題屬於數學家所謂「Dirichlet邊界值問題」裏的一般類型問題。為了令讀者更加更有親切感,我們會舉出一個日常生活的例子。如果我們將空氣吹入一杯牛奶內,會看到表面有一堆氣泡形成,其中一部分黏在杯邊(圖6)。肥皂泡的邊界可以在容器的內壁上自由移動(此處是玻璃),因此邊界不是完全被固定的。H A Schwarz在1872年觀察到,肥皂泡(或肥皂膜)會與容器內壁垂直接觸。這就是所謂的「自由邊界問題」。

圖6 - 黏在杯邊的氣泡(資料來源:https://www.masterfile.com/search/en/glass+of+milk+bubbles)
1816年,法國數學家Gergonne提出第一個有關極小曲面與自由邊界的幾何問題,但直到二十世紀三十年代,才由Richard Courant與他的學生對總體問題提出有系統的研究[6]。在任意形狀的容器裏,能否找出至少一個帶有自由邊界的極小曲面?這個問題雖然在過去幾十年中取得了重大進展,但直至最近才得到概括而肯定的解決[7]。我們借鑒F Almgren與他學生J Pitts[8]在三十年前提出的理論,名為「極小極大理論」,它的作用是在非常普通的情況下透過幾何測度論來構造極小曲面。Almgren與Pitts的極小極大理論最近再次掀起話題,因為學者出奇地發現到它與共形幾何(conformal geometry)[9]及紐結理論(knot theory)[10]中其他長期未被解決的問題有所關聯。更令人意想不到的是,極小極大理論會產生不止一個,而是無限個極小曲面 [11](通常均勻分佈在環繞空間(ambient space) [12] 內。
數學與物理學上的極小曲面 雖然極小曲面在我們熟悉的平面三維空間會更簡單、更直觀,但極小曲面的概念並不止於此。極小曲面亦存在於彎曲及更高維的空間。古典微分幾何學裏廣為人知的一點是,環繞空間的曲率會影響「直線」的性質(圖7)。我們可將極小曲面類比為「直線」的更高維版本;利用極小曲面這塊透鏡,我們就可以研究到周圍空間的幾何形狀。R Schoen與丘成桐運用極小曲面理論來證明廣義相對論 [13] 中的正質量猜想(positive mass conjecture)。 極小曲面在幾何流(geometric flow)中自然出現,令幾何拓撲學中有百年歷史的「龐加萊猜想」(Poincare Conjecture) 得到證明[14]。單位球(unit ball)的自由邊界極小曲面與形狀最佳化問題息息相關[15]。最近的研究顯示,黑洞的熵與AdS/CFT對偶(AdS/CFT correspondence)中出現的某些極小曲面的面積有關[16]。我們預計,極小曲面會在數學及物理學的諸多問題中擔當重要位置,因為只需看看周圍的環境,就會發覺到,極小曲面無處不在!
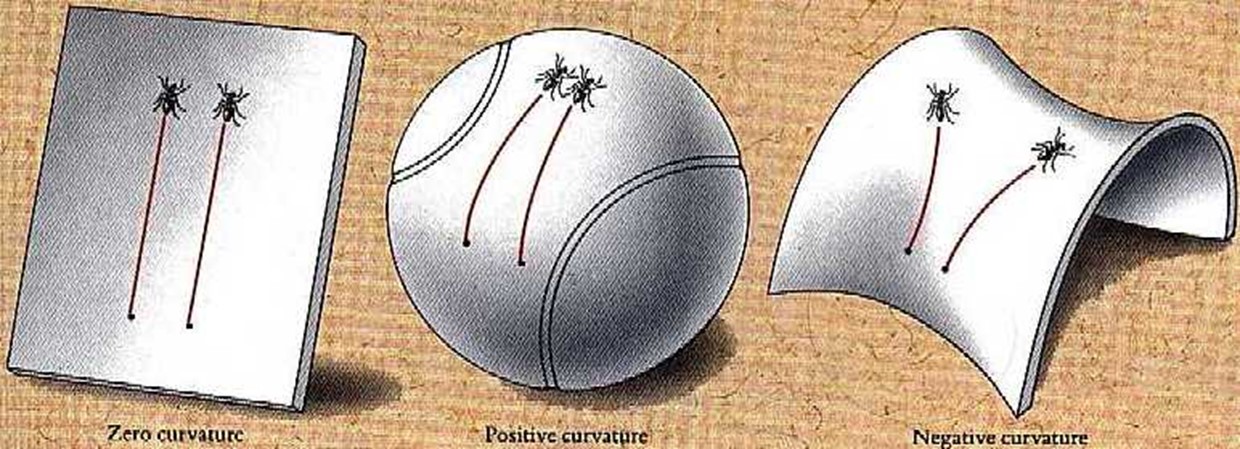
圖7 - 幾何形狀影響直線的特性。平面上的兩條平行線之間保持固定距離(左),而像網球的正彎曲空間裏,直線會有匯合的傾向(中);在像馬鞍的負彎曲空間裏則會散開(資料來源:http://gemma.ujf.cas.cz/~krejcirik/images/ants.jpg)
References
- O. Savin, “Phase Transitions, Minimal Surfaces and A Conjecture of De Giorgi”, Current Developments in Mathematics, 2010: 59-113 (2010)
- B. Winter et. al. “Coexistence of both gyroid chiralities in individual butterfly wing scales of Callophrys rubi” PNAS 112 (42), 12911-12916 (2015)
- J. Taylor, “The structure of singularities in soap-bubble-like and soap-film-like minimal surfaces”, Annals of Mathematics 103 (1976), 489-539
- K. Brakke, “The motion of a surface by its mean curvature”, Mathematical Notes, vol. 20. Princeton University Press, Princeton (1978)
- A. Figalli, X. Ros-Oton, J. Serra, “The singular set in the Stefan problem”, arXiv:2103.13379
- R. Courant, “Dirichlet principle, conformal mapping, and minimal surfaces”, Dover Publications (2005)
- M. M.-c. Li, X. Zhou, “Min-max theory for free boundary minimal hypersurfaces I: regularity theory”, Journal of Differential Geometry 118 (2021), no. 3, 487-553
- J. Pitts, “Existence and regularity of minimal surfaces on Riemannian manifolds”, Mathematical Notes, vol. 27, Princeton University Press, Princeton (1981)
- F.C. Marques, A. Neves, “Min-max theory and the Willmore Conjecture”, Annals of Mathematics 179 (2014), 683-782
- F.C. Marques, A. Neves, “Min-max theory and the energy of links”, Journal of the American Mathematical Society 29 (2016), 561-578
- A. Song, “Existence of infinitely many minimal hypersurfaces in closed manifolds”, arXiv: 1806.08816
- F.C. Marques, A. Neves, A. Song, “Equidistribution of minimal hypersurfaces for generic metrics”, Inventiones Mathematicae 216 (2019), 421-443
- R. Schoen, S.-T. Yau, “On the proof of the positive mass conjecture in general relativity”, Communications in Mathematical Physics 65 (1979), 45-76
- T. Colding, W. Minicozzi, “Width and finite extinction time of Ricci flow”, Geometry & Topology 12 (2008), 2537-2586
- A. Fraser, R. Schoen, “Sharp eigenvalue bounds and minimal surfaces in the ball”, Inventiones Mathematicae 203 (2016), 823-890
- S. Ryu, R. Takayanagi, “Aspects of Holographic Entanglement Entropy”, Journal of High Energy Physics 2006 (8): 045
作者︰
香港中文大學數學系副教授李文俊教授
2021年11月

