Minimal surfaces are amongst the most important objects studied in differential geometry. Apart from its intrinsic mathematical beauty, they appear naturally in a wide range of physical phenomena, for example, in phase transitions [1] and in the biophotonic nanostructures in butterfly wing scales [2] (Fig 1). Minimal surfaces also make their presence in material science, engineering, and even in art and architecture. Frei OTTO used minimal surfaces in several of his architectural designs including the 1972 Summer Olympic Games Stadium in Munich, Germany (Fig 2).

Fig 1 - Gyroid structures in butterfly wing scales (source: [2])

Fig 2 – The Olympiastadion situated at the heart of the Olympiapark München in northern Munich, the stadium was built as the main venue for the 1972 Summer Olympics (source: https://munich-info.info/olympic_stadium_munich/)
Soap films and Plateau’s experiments In fact, we do not need to be a scientist or an architect to understand what a minimal surface is. We all have early acquaintance with such surfaces in the form of soap films as well as their related cousin, soap bubbles. If you dip a piece of metal wire into soap solutions and take it out, you will see a thin layer of soap films bounded by the wire. For example, a flat disk will be formed for a round circular wire. If you take two parallel coaxial circles instead, then you will obtain a rotationally symmetric piece of soap film known as the catenoid (Fig 3). In the 19th century, the Belgian physicist and mathematician Joseph PLATEAU was the first to conduct extensive studies of soap films through experiments with different shapes of metal wire. Through his experimental observations, he formulated a set of laws – known as Plateau’s laws – that describe the shape and configuration of all possible soap films (Fig 4).

Fig 3 – Soap films showing the shape of a flat disk (left) and a catenoid (right) (source: http://soft-matter.seas.harvard.edu/index.php/Soap_films)

Fig 4 – Soap films demonstrating Plateau’s laws (source: "The Geometry of Soap Films and Soap Bubbles", F Almgren and J Taylor, Scientific American (1976))
The mathematics of soap films Plateau’s experiments were inspired by a mathematical question raised by Joseph-Louis LAGRANGE in 1760 – does an area-minimising surface always exist with a given boundary configuration? The underlying mechanism determining the shape of soap films is based on one principle – to achieve the least possible physical energy (which is roughly the area of the surface in the idealised situation). This simple idea, called the least action principle, can be used to derive many physical laws in a wide range of situations from Yang-Mills theory to Einstein’s theory of General Relativity. Although Plateau’s experiments have provided a zoo of models for soap films, it turns out to be a very difficult problem to establish the existence of such soap-film surfaces using rigorous mathematical language. It was not until 1930 that this problem was solved independently by Jesse DOUGLAS and Tibor RADÓ. It was a major breakthrough! This work is so important that Douglas was awarded the first Fields Medal, often known as the "Nobel Prize in Mathematics", in 1936 –. About 40 years later, Jean TAYLOR published [3] the first mathematical proof of Plateau’s laws, hence confirming Plateau’s observations in his soap film experiments more than a century ago.
The techniques used in the proof of Jean Taylor’s celebrated theorem are different from those of Douglas and Radó to solve Plateau’s problem. The ideas belong to a subject of mathematics called "Geometric Measure Theory" (GMT), which is a powerful tool in studying the general shapes and fine structures of objects (like soap films and soap bubbles) arising in geometric variational problems.
To get a glimpse of what GMT is about, let us, firstly, have a more elaborated discussion of what a "surface" is. In mathematics, a surface is a two-dimensional space which looks like a piece of elastic membrane at small scales. A surface is said to be "smooth" if every point has a well-defined "tangent plane" (which means it does not have any sharp edges or corners). An important technique in GMT is the blow-up process. Roughly speaking, if you want to understand the fine local structure around a point on the surface, you can take an imaginary microscope to zoom into the region around that point. When you increase the magnifying power of the microscope further and further, the surface would look more and more similar to a flat plane at a smooth point. In contrast, if you are zooming into a singular point (for example, the edges or vertices on a soap-film), then you are going to see some limit geometric shape which is different from a plane. By studying what limit shapes one can obtain through these blow-up processes, we can then infer the local structures around the singularities (Fig 5). This idea goes way beyond minimal surfaces but are crucial in the study of singularities arising in grain-boundary motion [4] and the interface of melting ice [5].
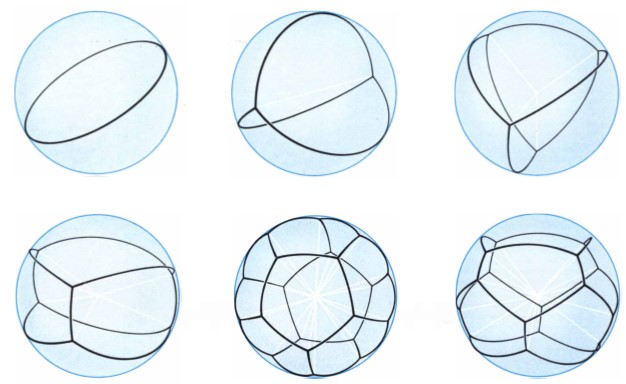
Fig 5 – Some possible limit geometric shape that may arise in a blow-up process (source: "The Geometry of Soap Films and Soap Bubbles", F Almgren and J Taylor, Scientific American (1976))
A free boundary problem for minimal surfaces Plateau’s problem belongs to a general type of problems that mathematicians referred to as Dirichlet boundary value problems. Perhaps a more familiar situation that we see in our daily lives is the following. If we blow air into a glass of milk, we will see bubble clusters forming on the surface and part of them will be adhered to the side of the glass (Fig 6). Instead of fixing the boundary configuration, here the boundary of the soap bubbles is allowed to move freely on the wall of the container (in this case, the glass). It was observed by H A SCHWARZ in 1872 that the soap bubbles (or soap films) will meet the container wall perpendicularly. This is known as the free boundary problem.

Fig 6 – Bubbles adhering to the side wall of the glass (source: https://www.masterfile.com/search/en/glass+of+milk+bubbles)
The first geometric problem leading to minimal surfaces with free boundary was posed by the French mathematician Gergonne in 1816, but the general problem was not systematically studied until 1930s by Richard COURANT and his students [6]. Can one find at least one minimal surface with free boundary inside a container of arbitrary shape? While important progress has been made throughout the last few decades, this question has just very recently been solved affirmatively in the full generality [7]. We draw on a 30-year-old theory by F Almgren and his student J Pitts [8] called min-max theory that has been devised to construct minimal surfaces using geometric measure theory under very general circumstances. The min-max theory of Almgren and Pitts has recently been revived due to its surprising connection to other longstanding open problems in conformal geometry [9] and knot theory [10]. An even more fascinating fact is that the min-max theory does not just produce one, but infinitely many minimal surfaces [11] which are typically uniformly distributed inside the ambient space [12].
Minimal surfaces in mathematics and physics Although it is simpler and more intuitive, the concept of minimal surfaces is not restricted to our familiar flat three-dimensional space (To: Martin: we do not quite understand how it would look like for a three-dimensional space which is flat). Minimal surfaces also exist in curved and higher dimensional spaces. It is a well-known fact from classical differential geometry that the curvature of the ambient space affects the behaviour of "straight lines" (Fig 7). Minimal surfaces, which can be regarded as a higher dimensional analogue of "straight lines", offer a lens through which we can study the geometry of the surrounding space. R SCHOEN and S T YAU use minimal surface theory to prove positive mass conjecture in General Relativity [13]. Minimal surfaces appear naturally in geometric flows which answers the century-old Poincare Conjecture in geometric topology [14]. Free boundary minimal surfaces in the unit ball are closely related to shape optimisation problems [15]. Recent research has suggested that the entropy of a black hole is related to the area of certain minimal surfaces arising in the AdS/CFT correspondence [16]. We expect to see minimal surfaces playing a major role in a broad spectrum of problems in mathematics and physics. Just look around us, minimal surfaces are everywhere!
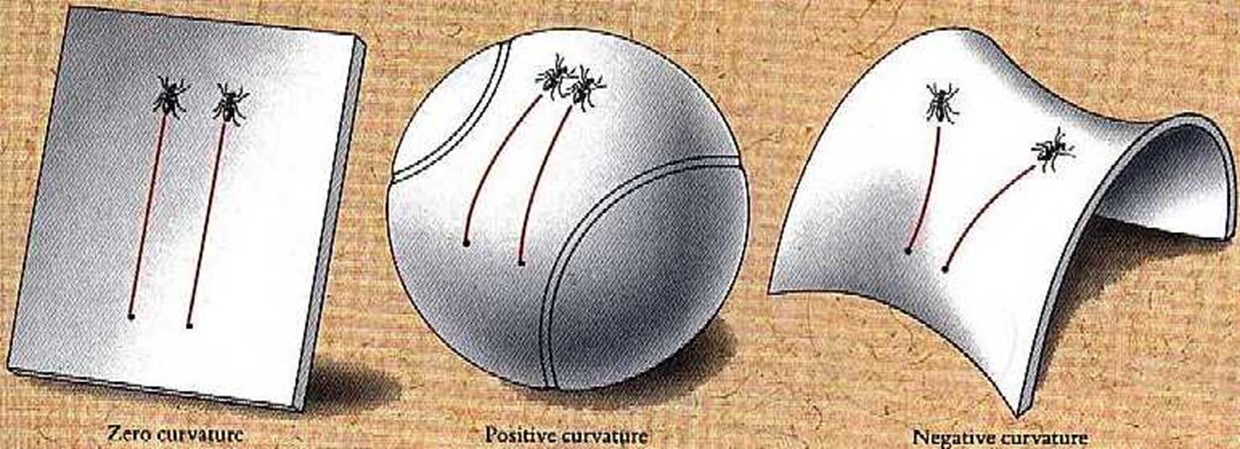
Fig 7 – Geometry affects the behaviour of straight lines. Two parallel lines on a flat plane remain a fixed distance from each other (left), while straight lines tend to converge to each other in a positively curved space like a tennis ball (middle) and diverge in a negatively curved space like a saddle (source: http://gemma.ujf.cas.cz/~krejcirik/images/ants.jpg)
References
- O. Savin, "Phase Transitions, Minimal Surfaces and A Conjecture of De Giorgi", Current Developments in Mathematics, 2010: 59-113 (2010)
- B. Winter et. al. "Coexistence of both gyroid chiralities in individual butterfly wing scales of Callophrys rubi" PNAS 112 (42), 12911-12916 (2015)
- J. Taylor, "The structure of singularities in soap-bubble-like and soap-film-like minimal surfaces", Annals of Mathematics 103 (1976), 489-539
- K. Brakke, "The motion of a surface by its mean curvature", Mathematical Notes, vol. 20. Princeton University Press, Princeton (1978)
- A. Figalli, X. Ros-Oton, J. Serra, "The singular set in the Stefan problem", arXiv:2103.13379
- R. Courant, "Dirichlet principle, conformal mapping, and minimal surfaces", Dover Publications (2005)
- M. M.-c. Li, X. Zhou, "Min-max theory for free boundary minimal hypersurfaces I: regularity theory", Journal of Differential Geometry 118 (2021), no. 3, 487-553
- J. Pitts, "Existence and regularity of minimal surfaces on Riemannian manifolds", Mathematical Notes, vol. 27, Princeton University Press, Princeton (1981)
- F.C. Marques, A. Neves, "Min-max theory and the Willmore Conjecture", Annals of Mathematics 179 (2014), 683-782
- F.C. Marques, A. Neves, "Min-max theory and the energy of links", Journal of the American Mathematical Society 29 (2016), 561-578
- A. Song, "Existence of infinitely many minimal hypersurfaces in closed manifolds", arXiv: 1806.08816
- F.C. Marques, A. Neves, A. Song, "Equidistribution of minimal hypersurfaces for generic metrics", Inventiones Mathematicae 216 (2019), 421-443
- R. Schoen, S.-T. Yau, "On the proof of the positive mass conjecture in general relativity", Communications in Mathematical Physics 65 (1979), 45-76
- T. Colding, W. Minicozzi, "Width and finite extinction time of Ricci flow", Geometry & Topology 12 (2008), 2537-2586
- A. Fraser, R. Schoen, "Sharp eigenvalue bounds and minimal surfaces in the ball", Inventiones Mathematicae 203 (2016), 823-890
- S. Ryu, R. Takayanagi, "Aspects of Holographic Entanglement Entropy", Journal of High Energy Physics 2006 (8): 045
Author:
Prof Martin LI, Associate Professor, Department of Mathematics, The Chinese University of Hong Kong
November 2021

