何謂逆問題?
對於科技界的許多問題,我們可以採集各種觀測數據,進而推斷出系統中的有用資訊,例如某些可以產生結果(或觀測數據)的物理參數。我們稱這種問題為「逆問題」,因為它是由結果推算出原因;而「正問題」則相反,是由原因推算出結果。逆問題能揭示出我們無法直接觀察到的參數,在系統識別、光學、雷達、聲納學、訊號處理、醫學造影、地球物理學、海洋學、天文學、遙距感應、非破壞測試等多個範疇均已獲廣泛應用。為更具體講解逆問題,在下文我們將開始慢慢揭開一個特定逆問題的神秘面紗:X 光計算機斷層成像。
X光攝影的由來
我們的旅程始於 1895 年,當時德國物理學家威廉.倫琴(Wilhelm Rontgen)正在用克鲁克斯管(Crookes tube)做實驗。他發現,某些由克魯克斯管發出的非可見光線,能穿透阻隔可見光線的黑色卡紙。他用「X」來命名這種射線,表示它是未知的射線類型。當他用感光板為妻子的手掌造影後,他很快就意識到能將射線用在醫療上。這張正是史上第一張人類身體部位的X光片。倫琴藉由這項發現獲頒首屆諾貝爾物理學獎。
時至今日,X光攝影(又名投影X光攝影或常規X光攝影)已普遍用於篩查肺炎、骨折、癌症、血管疾病;而在我們對抗新型冠狀病毒病的努力中,亦有派上用場。其原理是,當X光穿過病人身體時,X光會因在體內散射及被吸收而衰減。因此,我們可以從透射的X光在底片螢光幕探測器上的讀數推斷出與體內有關的有用資訊。粗略的看,我們可以將投影X光片當作是X光照射之下半透明的三維身體所投射出來的二維陰影。
从X光攝影到X光計算機斷層成像
雖然X光投影攝影很受歡迎,但它有一項重大缺陷,就是缺乏深度分辨率。具體而言,上下層組織的叠影有時會「隱藏」重要細節,並限制醫學診斷時的對比度。為解決這個問題, 醫學界採用了人體薄切片二維圖像斷層掃描,即是X 光計算機斷層成像 (X-ray computed tomography,CT)。CT的基本原理是以計算機來合併處理源由不同角度的多張X光投影片,從而產生身體斷層圖像,令診斷人員無需動手術切割即可看到身體內部。與X光投影攝影不同,CT所生成的圖象是利用數學方法處理測量數據而獲得的。1979年,物理學家Allan M CORMACK及電氣工程師Godfrey N HOUNSFIELD憑藉開發出CT而獲得諾貝爾生理學或醫學獎。
CT背後的數學變換
在一般的操作裏,CT掃描器會在每兩次X光照相之間,將病人環繞由頭至腳的軸心輕微旋轉,從而得出一連串不同角度的二維投影。投影片的每條水平線會為身體在該角度的二維軸向橫切面繪製一條一維投影。當集合所有水平線之後,每張投影片裏位於相同高度的每一條線就會包含與軸向橫切面相關的資訊,這正好與二维雷登變換(2D Radon transform)一致。更準確而言,變換時會將一個定義在平面上的函數(f)變成一個個定義在該平面上的直線所组成的空間上的函數(Rf)(函數 Rf 在一條特定直線上的值等於f在該直線上的線積分)。如使用數學語言來表達,則設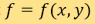 為平面
為平面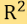 上定義的一個函數;將平面裏的定向直線構成的空間以兩個數字
上定義的一個函數;將平面裏的定向直線構成的空間以兩個數字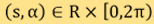 參數化, 當中
參數化, 當中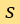 是線由來源點起計的距離,
是線由來源點起計的距離,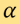 則是該線的法向量(normal vector)與X軸形成的角度。則雷登變換被定義為
則是該線的法向量(normal vector)與X軸形成的角度。則雷登變換被定義為

在CT裏,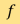 代表病人身體軸向橫切面的射線衰減係數,而CT掃描器的工作是當角度為
代表病人身體軸向橫切面的射線衰減係數,而CT掃描器的工作是當角度為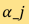 時,為一組離散的光路徑(用
時,為一組離散的光路徑(用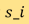 做標記)採集其雷登變換(以
做標記)採集其雷登變換(以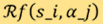 來表示)的數據。 雷登變換是1917年由數學家約翰.雷登提出,他另外亦提供了逆變換的方程式。我們廣泛使用的卷積反投影 (convolution back-projection, CBP) 算法,其基礎正是由這項逆變換所構成。該逆方程﹕
來表示)的數據。 雷登變換是1917年由數學家約翰.雷登提出,他另外亦提供了逆變換的方程式。我們廣泛使用的卷積反投影 (convolution back-projection, CBP) 算法,其基礎正是由這項逆變換所構成。該逆方程﹕
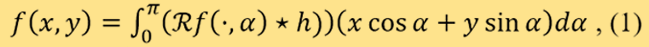
其中,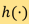 是傅利葉變換(Fourier transform)
是傅利葉變換(Fourier transform)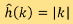 的一維函數,「
的一維函數,「 」則代表兩個一維函數的卷積,其方程式為
」則代表兩個一維函數的卷積,其方程式為
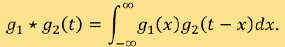
值得一提的是,雷登變換可以推廣到更高維的歐幾里得(Euclidean)空間,甚至黎曼流形(Riemannian manifold)。雷登變換的性質在數學的分支積分幾何裏已得到廣泛研究[5]。
數學難題——CT重建
借助逆方程式(1),CT重建似乎不難。但是,和我們期望的不同, 直接應用這條方程式通常會產生質素較差的圖像,原因是測量時必定會有噪訊。更嚴重的是,噪訊還可能會被逆變換(即函數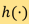 的卷積)放大。這是逆問題的典型特性,他們是「不適定的」(ill-posed problem)。更精確而言,根據數學家Jacques HADAMARD的定義,適定問題(well-posed problem)須符合三大條件﹕
的卷積)放大。這是逆問題的典型特性,他們是「不適定的」(ill-posed problem)。更精確而言,根據數學家Jacques HADAMARD的定義,適定問題(well-posed problem)須符合三大條件﹕
- 問題必須有解
- 解法只有一個。
- 即使數據有微小變化,解法仍然必須穩定。
相反,如果問題違反上述一項或多項條件,該問題就算是不適定問題。起初,數學家認為違反這些條件的問題並無實際意義或物理上的意義,而且無必要嘗試解這些問題。然而,後來我們得知,數學上不適定的逆問題在整個科學及工程界俯拾皆是。幸而,不適定問題可以利用極為強力的方法來解決——「正則化」(regularisation)。用正則化來解題似乎是萬試萬靈。最重要的例子之一,是由俄羅斯數學家兼地球物理學家Andrey Nikolayevich Tikhonov首次提出的吉洪諾夫正則化。正則化是逆問題界已獲廣泛研究的領域 [3]。
回到剛才的CT重建問題,由於它未能滿足第三項條件,因此屬於不適定類別。Ramachandranv與Lakshminarayan提供了一個巧妙的解決方法——用一項稱為Ram-Lak濾子(filter)的新函數代替卷積函數。該濾子的作用是模仿函數h在低頻部分的表現,同時又抑制其高頻部分的影響。這樣,逆變換時不穩定或對噪訊不敏感的部分會被正則化,而經過修正的重建方程式就能產生更佳的圖像。這類重建方法稱為「濾波反投影」(filtered back-projection),被用在過去四十年幾乎所有商用CT掃描器之中[6]。
更好的算法能造就更精良的CT掃描器?
因於醫療上要求更短的掃描時間及更少X光輻射量,CT系統正在迅速變化;曾經通用的濾波反投影算法正逐漸被新的重建方法取代。以二維的情況為例,我們可以先將二維域離散成N個像素,然後利用能在每個像素上取得常數值的函數來趨近衰減函數f。這樣,我們就可以用 中的向量
中的向量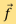 來表示
來表示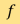 。每次測量
。每次測量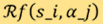 均會得出
均會得出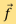 的線性函數。經過共
的線性函數。經過共 次測量後,我們得到一個有個未知數的線性方程組
次測量後,我們得到一個有個未知數的線性方程組 ,例如,
,例如,
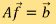
其中 是測量矩陣,
是測量矩陣,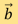 則對應測量數據。在一般情況下,我們會得出
則對應測量數據。在一般情況下,我們會得出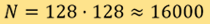 ,此為對應解象度為
,此為對應解象度為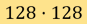 的圖象,而
的圖象,而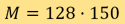 則是對應有128個等距角時,在每個角採集150條射線路徑的圖象。這個系統巨大得無法直接逆轉。在某些無法逐片重建圖像的更複雜掃描幾何形狀中,系統的尺寸甚至更大。由於涉及大量運算成本,因此可以解釋為何反投影算法仍然在商用CT系統中佔主導。另一方面,這類大型系統在數值線性代數領域亦引起了不少研究人員的興趣,研究界亦已開發多項選代技術(iterative technique),務求製造出令人滿意的解算器。其中一項是Kaczmarz方法,是由波蘭數學家Stefan KACZMARZ首先發現。這類依靠解算線性方程組的方法,名為代數重建技術。值得一提的是,由Hounsfield開發的第一部商用CT掃描器,所運用的正是代數重建技術。與反投影式的方法相比,迭代算法在減少某些偽影(artefact)及處理噪訊方面較有優勢。此外,在部分測量或不完整測量的情況(無法應用逆方程式),以及在希望減少X光量而不影響畫質的情況,迭代算法更有明顯優勢[4]。如要在重建中使用部分測量,以及在不增加X光量的情況下得到超解象度,則是新的難題,因為我們手上的方程式量未足以應付未知數。重建的問題則更加不適定,然而並非毫無對策。我們一般認為,一種圖像類別中的自由度數量(例如人肺)是遠小於圖像中的總象素數量。利用這種每個問題特有的稀疏性(sparsity),就可以將不適定性從本質上正則化。在這方面,稀疏性及壓縮感知的理論[2]可以提供所急需的理論基礎。諸如迭代的稀疏近似最小方差算法(Sparse Asymptotic Minimum Variance)的重建算法可以在無需要更高輻射量的情況下提供超解象度成像,並已引起不少研究員的興趣。[1].
則是對應有128個等距角時,在每個角採集150條射線路徑的圖象。這個系統巨大得無法直接逆轉。在某些無法逐片重建圖像的更複雜掃描幾何形狀中,系統的尺寸甚至更大。由於涉及大量運算成本,因此可以解釋為何反投影算法仍然在商用CT系統中佔主導。另一方面,這類大型系統在數值線性代數領域亦引起了不少研究人員的興趣,研究界亦已開發多項選代技術(iterative technique),務求製造出令人滿意的解算器。其中一項是Kaczmarz方法,是由波蘭數學家Stefan KACZMARZ首先發現。這類依靠解算線性方程組的方法,名為代數重建技術。值得一提的是,由Hounsfield開發的第一部商用CT掃描器,所運用的正是代數重建技術。與反投影式的方法相比,迭代算法在減少某些偽影(artefact)及處理噪訊方面較有優勢。此外,在部分測量或不完整測量的情況(無法應用逆方程式),以及在希望減少X光量而不影響畫質的情況,迭代算法更有明顯優勢[4]。如要在重建中使用部分測量,以及在不增加X光量的情況下得到超解象度,則是新的難題,因為我們手上的方程式量未足以應付未知數。重建的問題則更加不適定,然而並非毫無對策。我們一般認為,一種圖像類別中的自由度數量(例如人肺)是遠小於圖像中的總象素數量。利用這種每個問題特有的稀疏性(sparsity),就可以將不適定性從本質上正則化。在這方面,稀疏性及壓縮感知的理論[2]可以提供所急需的理論基礎。諸如迭代的稀疏近似最小方差算法(Sparse Asymptotic Minimum Variance)的重建算法可以在無需要更高輻射量的情況下提供超解象度成像,並已引起不少研究員的興趣。[1].
總結
CT是逆問題裏最成功的例子之一。運用數學模型後,現實世界中大多數逆問題都可以算是某種將無法直接觀察到的物理參數映射到測量值的數學變換。解決逆問題本質上其實就是找出逆變換。隨著在解決逆問題的路上已取得根本進展,以及有效率的數值方法得到發展,我們預計這些新元素最終能帶來重建算法上的突破,幫助我們以更善意、更健康的方式窺探內部,同時能兼顧圖像的質素。
參考資料
- H. Abeida; Q. Zhang; J. Li and N. Merabtine, Iterative Sparse Asymptotic Minimum Variance Based Approaches for Array Processing, IEEE Transactions on Signal Processing. IEEE. 61 (4): 933-944, (2013).
- D. L. Donoho, Compressed sensing, IEEE Transactions on Information Theory, vol. 52, no. 4, 1289-1306, (2006). doi: 10.1109/TIT.2006.871582.
- H. W. Engl, M. Hanke and A. Neubauer, Regularization of Inverse Problems, Springer, Netherlands, (2000). ISBN 978-0-7923-4157-4.
- C. L. Epstein, Introduction to the Mathematics of Medical Imaging, Societyfor Industrial and Applied Mathematics, 2nd Edition, (2007). ISBN: 978-0-89871-642-9.
- S. Helgason, Integral Geometry and Radon Transforms, Springer, (2011). ISBN 9781441960542.
- J. L. Prince and J. M. Links, Medical Imaging Signals and Systems, Pearson. 2nd edition, (2014). ISBN-13: 978-0132145183.
作者︰
香港科技大學數學系副教授張海教授
2021年9月