何谓逆问题?
对于科技界的许多问题,我们可以采集各种观测数据,进而推断出系统中的有用资讯,例如某些可以产生结果(或观测数据)的物理参数。我们称这种问题为「逆问题」,因为它是由结果推算出原因;而「正问题」则相反,是由原因推算出结果。逆问题能揭示出我们无法直接观察到的参数,在系统识别、光学、雷达、声纳学、讯号处理、医学造影、地球物理学、海洋学、天文学、遥距感应、非破坏测试等多个范畴均已获广泛应用。为更具体讲解逆问题,在下文我们将开始慢慢揭开一个特定逆问题的神秘面纱:X 光计算机断层成像。
X光摄影的由来
我们的旅程始于 1895 年,当时德国物理学家威廉.伦琴(Wilhelm Rontgen)正在用克鲁克斯管(Crookes tube)做实验。他发现,某些由克鲁克斯管发出的非可见光线,能穿透阻隔可见光线的黑色卡纸。他用「X」来命名这种射线,表示它是未知的射线类型。当他用感光板为妻子的手掌造影后,他很快就意识到能将射线用在医疗上。这张正是史上第一张人类身体部位的X光片。伦琴藉由这项发现获颁首届诺贝尔物理学奖。
时至今日,X光摄影(又名投影X光摄影或常规X光摄影)已普遍用于筛查肺炎、骨折、癌症、血管疾病;而在我们对抗新型冠状病毒病的努力中,亦有派上用场。其原理是,当X光穿过病人身体时,X光会因在体内散射及被吸收而衰减。因此,我们可以从透射的X光在底片萤光幕探测器上的读数推断出与体内有关的有用资讯。粗略的看,我们可以将投影X光片当作是X光照射之下半透明的三维身体所投射出来的二维阴影。
从X光摄影到X光计算机断层成像
虽然X光投影摄影很受欢迎,但它有一项重大缺陷,就是缺乏深度分辨率。具体而言,上下层组织的叠影有时会「隐藏」重要细节,并限制医学诊断时的对比度。为解决这个问题, 医学界采用了人体薄切片二维图像断层扫描,即是X 光计算机断层成像 (X-ray computed tomography,CT)。 CT的基本原理是以计算机来合并处理源由不同角度的多张X光投影片,从而产生身体断层图像,令诊断人员无需动手术切割即可看到身体内部。与X光投影摄影不同,CT所生成的图象是利用数学方法处理测量数据而获得的。 1979年,物理学家Allan M CORMACK及电气工程师Godfrey N HOUNSFIELD凭借开发出CT而获得诺贝尔生理学或医学奖。
CT背后的数学变换
在一般的操作里,CT扫描器会在每两次X光照相之间,将病人环绕由头至脚的轴心轻微旋转,从而得出一连串不同角度的二维投影。投影片的每条水平线会为身体在该角度的二维轴向横切面绘制一条一维投影。当集合所有水平线之后,每张投影片里位于相同高度的每一条线就会包含与轴向横切面相关的资讯,这正好与二维雷登变换(2D Radon transform)一致。更准确而言,变换时会将一个定义在平面上的函数(f)变成一个个定义在该平面上的直线所组成的空间上的函数(Rf)(函数 Rf 在一条特定直线上的值等于f在该直线上的线积分)。如使用数学语言来表达,则设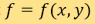 为平面
为平面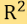 上定义的一个函数;将平面里的定向直线构成的空间以两个数字
上定义的一个函数;将平面里的定向直线构成的空间以两个数字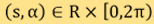 参数化, 当中
参数化, 当中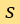 是线由来源点起计的距离,
是线由来源点起计的距离,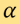 则是该线的法向量(normal vector)与X轴形成的角度。则雷登变换被定义为
则是该线的法向量(normal vector)与X轴形成的角度。则雷登变换被定义为

在CT里,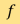 代表病人身体轴向横切面的射线衰减系数,而CT扫描器的工作是当角度为
代表病人身体轴向横切面的射线衰减系数,而CT扫描器的工作是当角度为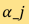 时,为一组离散的光路径(用
时,为一组离散的光路径(用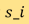 做标记)采集其雷登变换(以
做标记)采集其雷登变换(以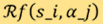 来表示)的数据。雷登变换是1917年由数学家约翰.雷登提出,他另外亦提供了逆变换的方程式。我们广泛使用的卷积反投影 (convolution back-projection, CBP) 算法,其基础正是由这项逆变换所构成。该逆方程﹕
来表示)的数据。雷登变换是1917年由数学家约翰.雷登提出,他另外亦提供了逆变换的方程式。我们广泛使用的卷积反投影 (convolution back-projection, CBP) 算法,其基础正是由这项逆变换所构成。该逆方程﹕
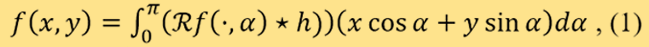
其中,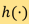 是傅利叶变换(Fourier transform)
是傅利叶变换(Fourier transform)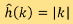 的一维函数,「
的一维函数,「 」则代表两个一维函数的卷积,其方程式为
」则代表两个一维函数的卷积,其方程式为
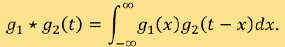
值得一提的是,雷登变换可以推广到更高维的欧几里得(Euclidean)空间,甚至黎曼流形(Riemannian manifold)。雷登变换的性质在数学的分支积分几何里已得到广泛研究[5]。
数学难题——CT重建
借助逆方程式(1),CT重建似乎不难。但是,和我们期望的不同, 直接应用这条方程式通常会产生质素较差的图像,原因是测量时必定会有噪讯。更严重的是,噪讯还可能会被逆变换(即函数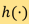 的卷积)放大。这是逆问题的典型特性,他们是「不适定的」(ill-posed problem)。更精确而言,根据数学家Jacques HADAMARD的定义,适定问题(well-posed problem)须符合三大条件﹕
的卷积)放大。这是逆问题的典型特性,他们是「不适定的」(ill-posed problem)。更精确而言,根据数学家Jacques HADAMARD的定义,适定问题(well-posed problem)须符合三大条件﹕
- 问题必须有解
- 解法只有一个。
- 即使数据有微小变化,解法仍然必须稳定。
相反,如果问题违反上述一项或多项条件,该问题就算是不适定问题。起初,数学家认为违反这些条件的问题并无实际意义或物理上的意义,而且无必要尝试解这些问题。然而,后来我们得知,数学上不适定的逆问题在整个科学及工程界俯拾皆是。幸而,不适定问题可以利用极为强力的方法来解决——「正则化」(regularisation)。用正则化来解题似乎是万试万灵。最重要的例子之一,是由俄罗斯数学家兼地球物理学家Andrey Nikolayevich Tikhonov首次提出的吉洪诺夫正则化。正则化是逆问题界已获广泛研究的领域 [3]。
回到刚才的CT重建问题,由于它未能满足第三项条件,因此属于不适定类别。 Ramachandranv与Lakshminarayan提供了一个巧妙的解决方法——用一项称为Ram-Lak滤子(filter)的新函数代替卷积函数。该滤子的作用是模仿函数h在低频部分的表现,同时又抑制其高频部分的影响。这样,逆变换时不稳定或对噪讯不敏感的部分会被正则化,而经过修正的重建方程式就能产生更佳的图像。这类重建方法称为「滤波反投影」(filtered back-projection),被用在过去四十年几乎所有商用CT扫描器之中[6]。
更好的算法能造就更精良的CT扫描器?
因于医疗上要求更短的扫描时间及更少X光辐射量,CT系统正在迅速变化;曾经通用的滤波反投影算法正逐渐被新的重建方法取代。以二维的情况为例,我们可以先将二维域离散成N个像素,然后利用能在每个像素上取得常数值的函数来趋近衰减函数f。这样,我们就可以用 中的向量
中的向量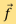 来表示
来表示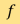 。每次测量
。每次测量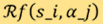 均会得出
均会得出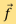 的线性函数。经过共
的线性函数。经过共 次测量后,我们得到一个有个未知数的线性方程组
次测量后,我们得到一个有个未知数的线性方程组 ,例如,
,例如,
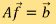
其中 是测量矩阵,
是测量矩阵,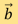 则对应测量数据。在一般情况下,我们会得出
则对应测量数据。在一般情况下,我们会得出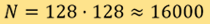 ,此为对应解象度为
,此为对应解象度为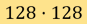 的图象,而
的图象,而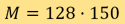 则是对应有128个等距角时,在每个角采集150条射线路径的图象。这个系统巨大得无法直接逆转。在某些无法逐片重建图像的更复杂扫描几何形状中,系统的尺寸甚至更大。由于涉及大量运算成本,因此可以解释为何反投影算法仍然在商用CT系统中占主导。另一方面,这类大型系统在数值线性代数领域亦引起了不少研究人员的兴趣,研究界亦已开发多项选代技术(iterative technique),务求制造出令人满意的解算器。其中一项是Kaczmarz方法,是由波兰数学家Stefan KACZMARZ首先发现。这类依靠解算线性方程组的方法,名为代数重建技术。值得一提的是,由Hounsfield开发的第一部商用CT扫描器,所运用的正是代数重建技术。与反投影式的方法相比,迭代算法在减少某些伪影(artefact)及处理噪讯方面较有优势。此外,在部分测量或不完整测量的情况(无法应用逆方程式),以及在希望减少X光量而不影响画质的情况,迭代算法更有明显优势[4]。如要在重建中使用部分测量,以及在不增加X光量的情况下得到超解象度,则是新的难题,因为我们手上的方程式量未足以应付未知数。重建的问题则更加不适定,然而并非毫无对策。我们一般认为,一种图像类别中的自由度数量(例如人肺)是远小于图像中的总象素数量。利用这种每个问题特有的稀疏性(sparsity),就可以将不适定性从本质上正则化。在这方面,稀疏性及压缩感知的理论[2]可以提供所急需的理论基础。诸如迭代的稀疏近似最小方差算法(Sparse Asymptotic Minimum Variance)的重建算法可以在无需要更高辐射量的情况下提供超解象度成像,并已引起不少研究员的兴趣。 [1].
则是对应有128个等距角时,在每个角采集150条射线路径的图象。这个系统巨大得无法直接逆转。在某些无法逐片重建图像的更复杂扫描几何形状中,系统的尺寸甚至更大。由于涉及大量运算成本,因此可以解释为何反投影算法仍然在商用CT系统中占主导。另一方面,这类大型系统在数值线性代数领域亦引起了不少研究人员的兴趣,研究界亦已开发多项选代技术(iterative technique),务求制造出令人满意的解算器。其中一项是Kaczmarz方法,是由波兰数学家Stefan KACZMARZ首先发现。这类依靠解算线性方程组的方法,名为代数重建技术。值得一提的是,由Hounsfield开发的第一部商用CT扫描器,所运用的正是代数重建技术。与反投影式的方法相比,迭代算法在减少某些伪影(artefact)及处理噪讯方面较有优势。此外,在部分测量或不完整测量的情况(无法应用逆方程式),以及在希望减少X光量而不影响画质的情况,迭代算法更有明显优势[4]。如要在重建中使用部分测量,以及在不增加X光量的情况下得到超解象度,则是新的难题,因为我们手上的方程式量未足以应付未知数。重建的问题则更加不适定,然而并非毫无对策。我们一般认为,一种图像类别中的自由度数量(例如人肺)是远小于图像中的总象素数量。利用这种每个问题特有的稀疏性(sparsity),就可以将不适定性从本质上正则化。在这方面,稀疏性及压缩感知的理论[2]可以提供所急需的理论基础。诸如迭代的稀疏近似最小方差算法(Sparse Asymptotic Minimum Variance)的重建算法可以在无需要更高辐射量的情况下提供超解象度成像,并已引起不少研究员的兴趣。 [1].
总结
CT是逆问题里最成功的例子之一。运用数学模型后,现实世界中大多数逆问题都可以算是某种将无法直接观察到的物理参数映射到测量值的数学变换。解决逆问题本质上其实就是找出逆变换。随着在解决逆问题的路上已取得根本进展,以及有效率的数值方法得到发展,我们预计这些新元素最终能带来重建算法上的突破,帮助我们以更善意、更健康的方式窥探内部,同时能兼顾图像的质素。
参考资料
- H. Abeida; Q. Zhang; J. Li and N. Merabtine, Iterative Sparse Asymptotic Minimum Variance Based Approaches for Array Processing, IEEE Transactions on Signal Processing. IEEE. 61 (4): 933-944, (2013).
- D. L. Donoho, Compressed sensing, IEEE Transactions on Information Theory, vol. 52, no. 4, 1289-1306, (2006). doi: 10.1109/TIT.2006.871582.
- H. W. Engl, M. Hanke and A. Neubauer, Regularization of Inverse Problems, Springer, Netherlands, (2000). ISBN 978-0-7923-4157-4.
- C. L. Epstein, Introduction to the Mathematics of Medical Imaging, Societyfor Industrial and Applied Mathematics, 2nd Edition, (2007). ISBN: 978-0-89871-642-9.
- S. Helgason, Integral Geometry and Radon Transforms, Springer, (2011). ISBN 9781441960542.
- J. L. Prince and J. M. Links, Medical Imaging Signals and Systems, Pearson. 2nd edition, (2014). ISBN-13: 978-0132145183.
作者︰
香港科技大学数学系副教授张海教授
2021年9月