(1) 引言
如果你撥動一條小提琴的琴弦,琴弦振動的同時,亦驅使它附近的空氣粒子振動,形成聲波在空氣中傳播,這就是為什麼你可以聽到琴音。不過,這樂音不會持久。在發出聲波的同時,琴弦會損失它振動的能量。所以,琴弦的振動會衰減,琴音亦然。
有趣的是,受擾動的黑洞都有類似的現象。當兩個黑洞相撞後,它們會合併成一個更大但被扭曲了的黑洞,同時產生重力波。這個被扭曲了的黑洞就是受擾動的黑洞的一個例子。重力波其實就是新形成的黑洞周圍時空的振盪。跟小提琴琴弦相似的是,這些時空的振盪不會持久,因為黑洞是一種具有事件視界的天體。事件視界像是黑洞的一個只可以單向行車的高速公路。任何物件,一旦進入了事件視界,就無法離開。所以在黑洞附近傳播的重力波,要不就是耗散到黑洞的事件視界,要不就是傳播到離黑洞很遠的地方,遠至我們都可以探測到。無論如何,在黑洞附近的重力波總是在散失它的能量,黑洞的振盪亦然。當這些振盪減到很弱時,被扭曲了的黑洞就會變成一個很安靜的靜態黑洞。由於黑洞振盪的衰減過程類似於樂器(例如一個響鈴)發出的樂音的衰減,黑洞振盪的衰減亦都叫做「鈴盪」。就像一條琴弦都有不同的振盪模態(基音和泛音),黑洞振盪都有不同的振盪模態。這些振盪模態命名為黑洞的準簡正模(quasinormal modes),相關的振動頻率則稱為準簡正模頻率(quasinormal-mode frequency)。
黑洞鈴盪不單純是理論物理的一個研究課題,這是一個實在的天文物理現象,打從我們由先進激光干涉儀重力波觀測站(the Advanced Laser Interferometer Gravitational-Wave Observatory, aLIGO)第一次直接量度到重力波時,我們就已經觀察到黑洞鈴盪。首次直接探測到的重力波訊號(GW150914)的末段,就清楚顯出一個由相重力波波源所形成的新黑洞所發出的鈴盪訊號。自此,天體物理學家就廣泛地研究重力波訊號中的鈴盪訊號。
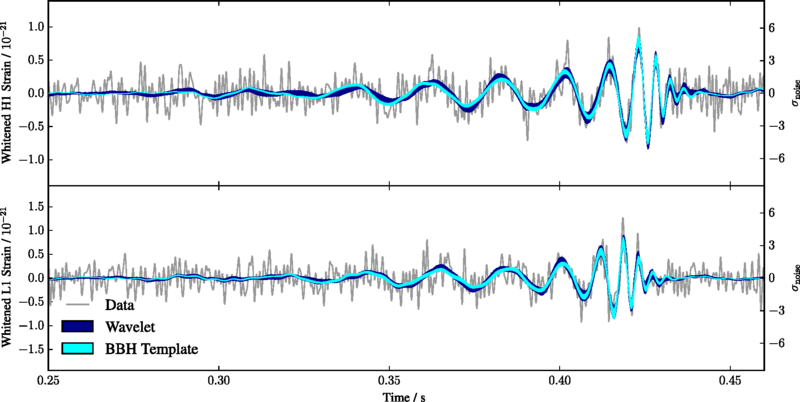
圖1: 先進激光干涉儀重力波觀測站第一次直接量度到重力波時的重力波訊號。在訊號的末段,我們可見一個黑洞振動的衰減。圖片取自[1]。
(2) 為什麼要關心黑洞鈴盪?
但為什麼天體物理學家很熱衷於研究黑洞鈴盪?筆者認為有兩大理由。
首先,鈴盪訊號是一個獨特而有效的探究工具,讓我們去研究基礎物理中未能解答的問題,例如愛因斯坦的廣義相對論在強重力的時空中—例如事件視界附近—是否還是正確的?相對論是一個斐然的理論,把重力作用演繹為時空的幾何效應,它亦代表了我們對時空的最佳解讀。但是,廣義相對論亦有些地方不能提供令人滿意的解釋,例如重力的量子本質。這些都反映廣義相對論有其局限,需要增補。但從何著手?為了揭示廣義相對論需要修補的地方,科學家進行了大量實驗,務求檢驗廣義相對論。不過可能令到某些物理學家失望的是,廣義相對論暫時都通過了所有的測試!但是,大部份這些測試都只涉及較弱的重力場,因為此前的測試,大都是在地球上或者是太陽系或星系內進行的。廣義相對論通過了這些全部的測試,反映廣義相對論要是失效的話,它只可以在重力非常強的時空—例如事件視界周圍—崩潰。要是廣義相對論真的不能正確描述強重力時空和黑洞振盪的動態的話,那我們將會觀察到跟廣義相對論預測不同的黑洞振盪模式。換言之,分析鈴盪訊號是測試廣義相對論在強重力時空中表現的理想工具。
第二,在研究黑洞振動的同時,我們會發展出多種數學工具。這些數學工具,都可以推動不同範疇的科研。為了正確了解鈴盪訊號,我們必須預先理解黑洞振動的模式。數學上,黑洞振盪由一組偏微分方程(partial differential equations)所描述。所謂偏微分方程,其實是偏導數(partial derivatives)所需要滿足的數學關係。而偏導數描述的是一個量怎樣隨住幾個不同的有關變量而改變[2,3]。研究黑洞擾動時,這些偏微分方程刻畫了黑洞的振幅怎樣隨住時間和位置而改變。除了黑洞物理外,偏微分方程在其他科研範疇都有廣泛應用。與日常生活有關的例子包括股票市場、天氣預報、電話通訊、光纖網絡和生物物理。通常偏微分方程都是很難解的,而描述黑洞振動的方程亦無例外。要克服這些數學挑戰,包括筆者在內的黑洞物理學家,致力發展新穎的數學技巧去解開這些複雜的方程式。這些數學技巧,亦可以用於解開出現於其他研究範疇的偏微分方程。
(3) 我們可以學到什麼?
正如一位專業小提琴演奏家聽到一個琴音,就可以立即辨別出琴音的音調、琴弦的粗幼和琴馬的狀態;一位鑽研黑洞的物理學家亦可透過仔細分析鈴盪訊號中,就可以推敲出黑洞的各樣特性。如圖一所示,一個鈴盪訊號是衰減的振盪。物理學上,一個衰減的振動可以用兩個數字去描述:頻率—振動的快慢和衰減期—振動消減的率。根據廣義相對論,黑洞的質量和轉動速率就完全決定了所有振動模式的頻率和衰減期。一個質量較大的黑洞振動頻率較慢;一個轉動得更快的黑洞,我們通常可以觀察到的振動模態就會更持久。故此,透過量度鈴盪訊號中的振動頻率和衰減期,我們可以計算出黑洞的質量和轉動速率。除此之外,我們更可以透過比對量度的和廣義相對論預測的振動頻率和衰減期,去檢視廣義相對論是否正確描述了黑洞事件視界附近的動力學。綜合所有迄今已觀察到的鈴盪訊號,物理學家尚未觀察到黑洞違反廣義相對論的跡象。可能令人失望亦可能令人心安,廣義相對論又再通過了一次測試。不過我們毋須過度失望,亦不能安於現況,因為這些結果歸根究底還是受到探測器的敏感度所限。換言之,我們僅是在觀察儀器的敏感度所容許的範圍內沒有觀察到廣義相對論失效的跡象。而先進激光干涉儀重力波觀測站和處女座重力波團隊探測器剛剛已再重新啟動,它將會以前所未有的敏感度去偵測重力波訊號。我們會否觀察到廣義相對論失效的跡象呢?且讓我們拭目以待。
(4) 我們如向從中學習?
但要正確和充分明白這些測試廣義相對論的結果,我們必先了解黑洞要是違反廣義相對論的話,會發出怎樣的鈴盪訊號。否則,即使我們真的偵測到廣義相對論失效的跡象,我們都可能會誤當這些跡象是另一個正常黑洞的鈴盪訊號,只是質量和轉動速率有所不同。為此,我們要廣泛地研究種種廣義相對論失效時黑洞鈴盪的訊號。
如上所述,要研究黑洞振動,我們要解開一組冗長的偏微分方程。要考慮到黑洞的自轉的話,方程式就更長了。但另一方面,由於已觀察到的黑洞中,有些自轉得很快,我們不可以忽略黑洞自轉。考慮到自轉後,這些偏微分方程確切有多繁複?如果你想把當中最短的一條方程打印到A4紙上,你需要56頁!而你不單要解開一條,你起碼要同時解開至少六條更長的方程式。對於廣義相對論所描述的黑洞,我們尚且可以根據它們獨有的幾何性質來利用一些高明的數學技巧以簡化這些冗長的方程式至一條。但是對於違反廣義相對論的自轉黑洞,我們不能重施故技,因為這些黑洞沒有相同的幾何性質。故此,我們現有的大部分方法,都只夠我們用來研究轉動得很慢的黑洞在不遵守廣義相對論時的振盪情形。在沒有了解到自轉黑洞在違反廣義相對論時的鈴盪,我們無法利用已經探測了的鈴盪訊號去透切地測試廣義相對論。
為了解決這個問題,筆者在伊利諾大學厄巴納-香檳分校跟尼古拉斯.苑尼斯教授和柏迪.華格里博士合作,正在發展一套方法在不需化解方程的情況下,直接解出這些冗長的偏微分方程。由於在不同情況下振動的黑洞,相關的偏微分方程都有類似的數學結講,要是我們可以直接解出這些偏微分方程而毋須化解的話,我們就可以直接把我們的方法,用在研究轉動黑洞在不同情況下的振盪,包括廣義相對論失效或者黑洞附近存在暗物質時的情形。
這套方法的關鍵在於我們把代表黑洞振幅的量預先表達成譜函數(spectral function)的綫性組合。譜函數是一類非常獨特的函數,因為它們可以用來很準確地擬近其他函數。而所謂的綫性組合,就是把譜函數,適當乘上一個合適的權重(稱為譜系數,spectral coefficient),再進行加減。這是一個很有用的性質,因為不是每一種函數都是基礎函數,例如對數函數、指數函數,和滿足各樣微分方程的函數。這些數學函數的性質並不顯而易見。另一邊廂,物理學家都熟識譜函數,用它們時也很方便。利用譜函數來擬近其他函數通常都可以幫助物理計算。舉例,如果我們想擬近圖二中藍線所代表的函數(涉及到指數函數),我們只需要6個譜函數就辦到,而且準確的程度是擬近出來的函數(紅線)和原本的函數在圖2中根本看不出任何分別。
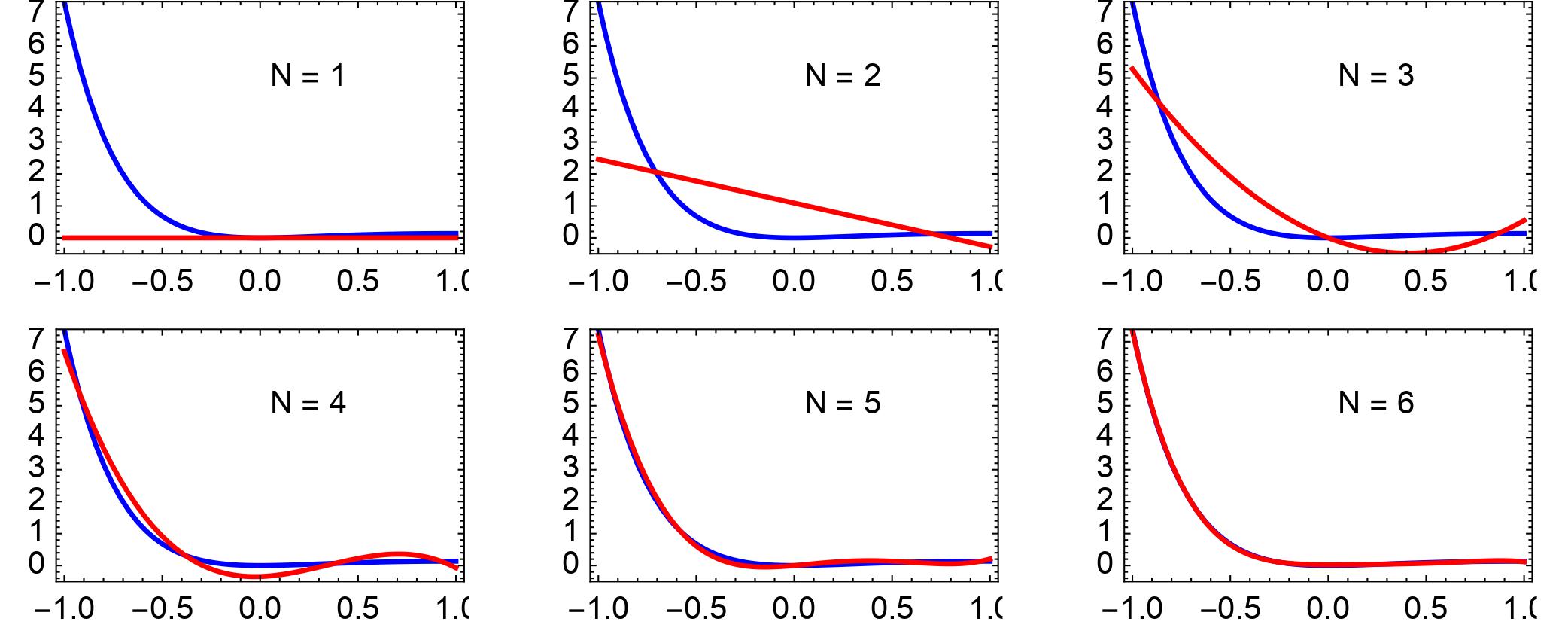
圖2: 譜函數一個有趣的性質是它們可以用來擬近其他函數。例如如有我的想擬近圖中藍色線所代表的函數,我們只需要用6個譜函數就可以很準確地擬近,致使我們的擬近和原本的函數視覺上幾乎沒有分別。圖片取自[4]。
譜函數的這特性在求解偏微分方程時就大派用場。如果我們先把滿足方程的未知函數寫成譜函數的綫性組合,那原先的偏微分方程就會變成譜系數的代數方程。一般而言,代數方程都比微分方程易解得多。作為發展這方法的第一步,我們先把這方法運用在不自轉但又遵守廣義相對論的黑洞,看看我們可否用這方法計算出這簡單黑洞已知的振動頻率[5]。結果就如圖三所示,運用譜方法我們可以極準確地算出這黑洞的振動頻率。圖3中的藍點是我們用譜方法計算出的頻率,而黑色交叉就是已知的頻率。只要我們用足夠多的譜函數,我們就可以準確計算到黑洞的準簡正模頻率。
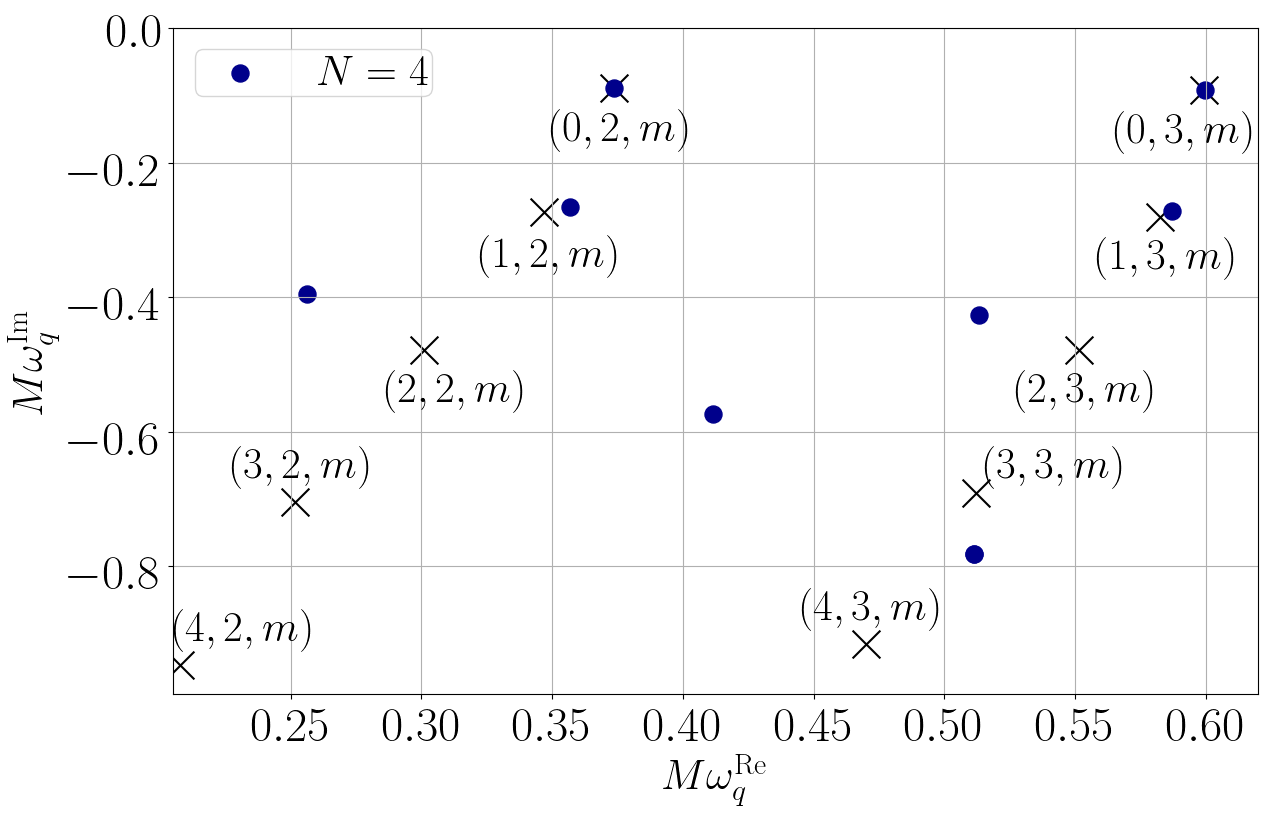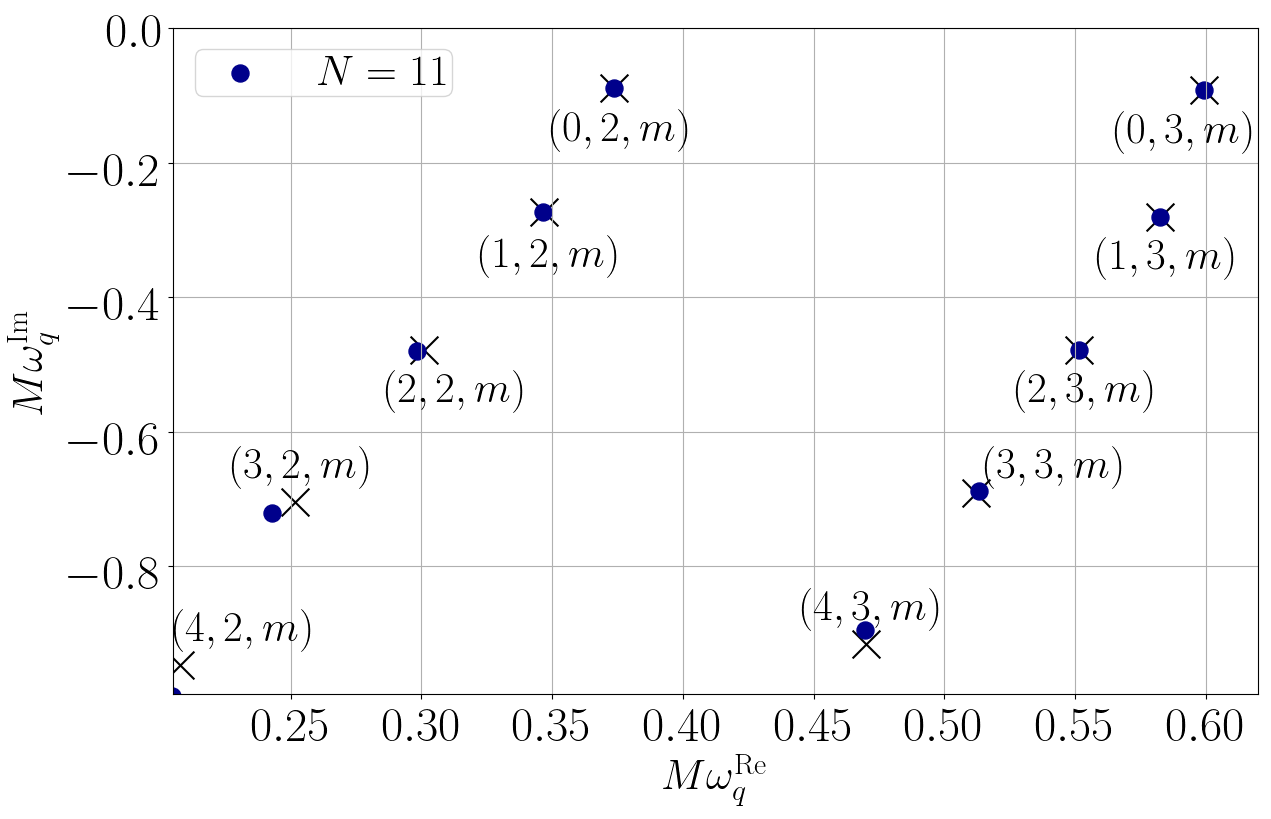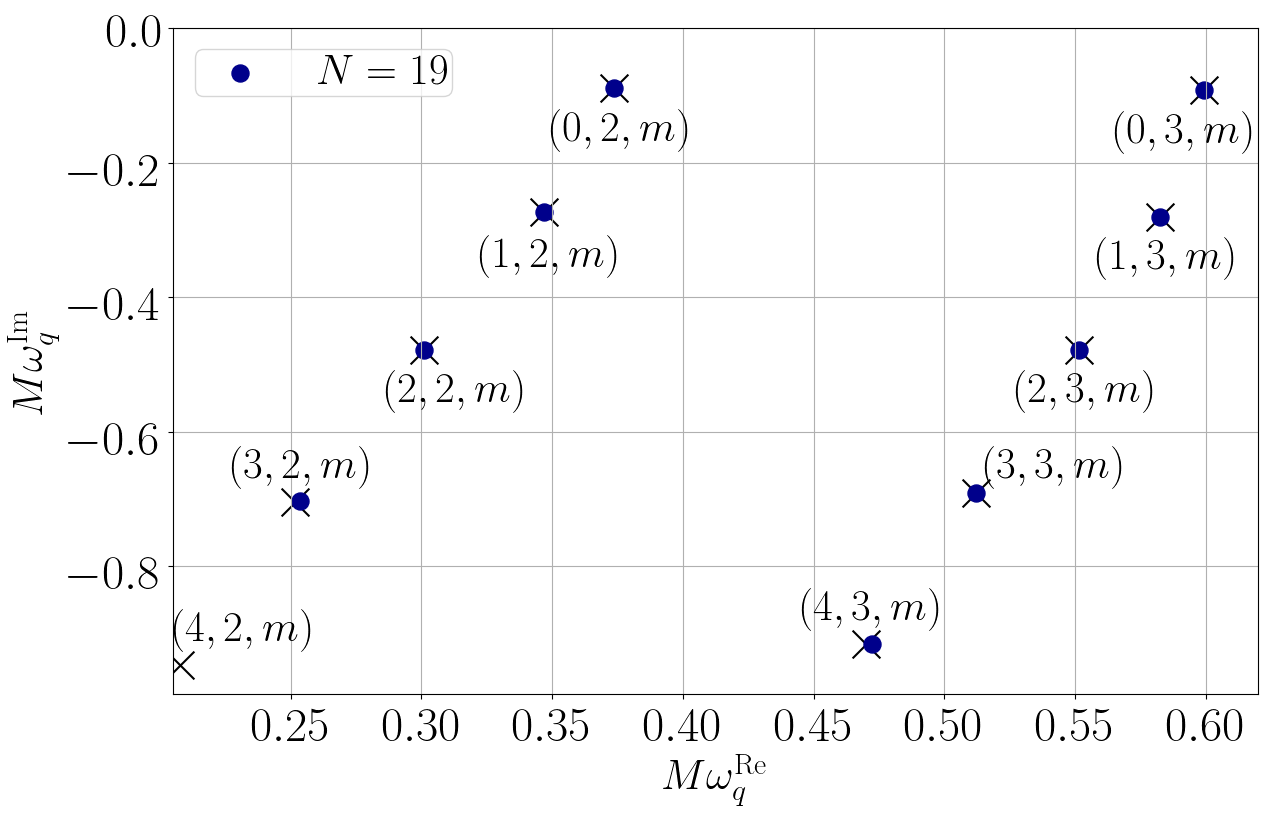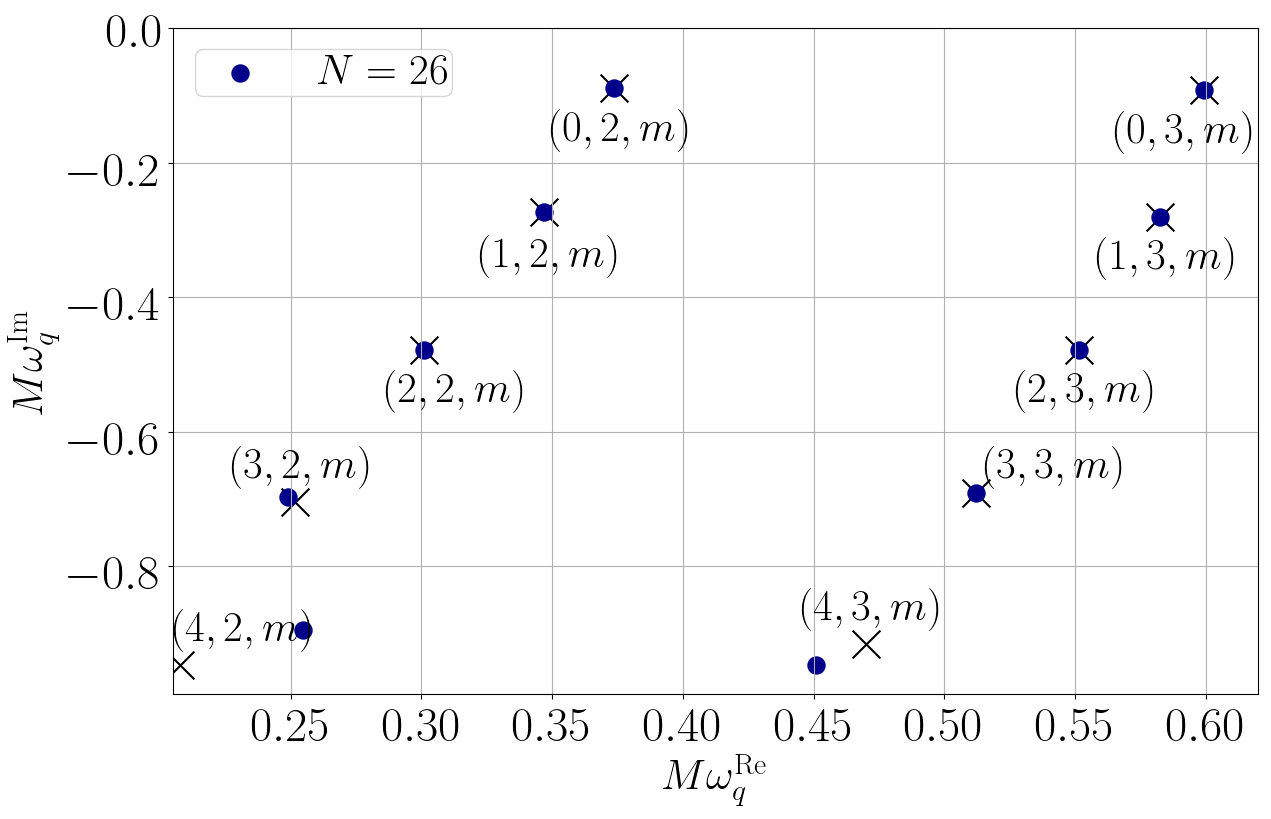
圖3: 我們用我們的方法計算不自轉但又遵守廣義相對論的黑洞的振動頻率(藍點)。當我們用上愈來愈多的譜函數(數目由N表示),我們的結果就跟已知的頻率(黑色交叉)愈趨吻合。圖片修改自[5]。
我們現正致力繼續發展這方法,令它可以用到廣義相對論中的轉動黑洞上。如果我們亦可以準備地算出這類黑洞的振動頻率,我們就可以確認我們的方法準確無誤,而且可以運用到其他用現有方法無法研究的黑洞上。在往年由香港桂冠論壇主辦的智者.智講青年科學家焦點小組(天文學)上,我已經展示過這方法在轉動黑洞上的初步結果[6]。我們現正準備相關的論文,交代這個運用譜方法的詳細步驟。
(5) 展望
計算出黑洞的準簡正模頻率只是第一步。得出不同黑洞的準簡正模譜後,我們須用這個譜來對比我們觀察到黑洞鈴盪訊號,從而推敲廣義相對論需要修正的方向和程度。這些計算和觀察都能令我們更好的去聆聽和了解黑洞振盪發出的樂音,從而去了解我們身處的宇宙。
延伸閱讀
- 基普.索恩教授著《黑洞和時空扭曲》的第十章
- Pedro G. Ferreira教授著 《完美的理論:一整個世紀的天才與廣義相對論之戰》
- 丘成桐教授和史蒂夫.納迪斯教授著《丘成桐談空間的內在形狀--幾何、弦論和宇宙中隱藏起來的維度》第五章
鳴謝
筆者在此感謝程國平先生、盧樂知先生和尼古拉斯.苑尼斯教授對本文初稿的意見。
參考資料︰
- Properties of the Binary Black Hole Merger GW150914, B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), Phys. Rev. Lett. 116, 241102, https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.116.241102
- 丘成桐教授和史蒂夫.納迪斯教授著《丘成桐談空間的內在形狀--幾何、弦論和宇宙中隱藏起來的維度》第五章有關於偏微分方程更詳細的科普導引
- 讀者要是中學時有學過微積分,可能會記得導數的概念。這導數叫做常導數(ordinary derivative),因為只涉及一個量怎樣隨另一個量改變。偏導數涉及的是一個量隨幾個量改變,故此偏導數可以視為常導數的延伸。
- A new approach and code for spinning black holes in modified gravity, by Pedro G. S. Fernandes, David J. Mulryne, https://arxiv.org/abs/2212.07293
- Spectral Method for the Gravitational Perturbations of Black Holes: Schwarzschild Background Case, Adrian Ka-Wai Chung, Pratik Wagle, Nicolas Yunes, accepted for publication by Physical Review D, https://arxiv.org/abs/2302.11624
- https://www.youtube.com/watch?v=MDeALFtz-Uc&list=PLkIh51n7eBb2Y5f559D4wTsY2L4GPH2hc&index=2&ab_channel=HongKongLaureateForum
作者︰
鍾嘉唯先生
伊利諾大學厄巴納-香檳分校物理系博士後研究員
伊利諾高等宇宙研究所成員
2023年10月

