(1) Introduction

If you pluck a violin string, the string vibrates, driving the air particles around the string to oscillate too, setting up sound waves that propagate in the air. That is why you will hear a note. However, the note will not last long. Through generating sound, the string loses its vibrational energy in the air. The vibrations of the violin string decay. So does the note.

Interestingly, a similar phenomenon occurs in perturbed black holes. As two black holes collide, they will merge into one larger and distorted black hole and generate enormous gravitational waves. The distorted black hole is an example of perturbed black hole. These gravitational waves are the oscillations of space-time near the new black hole. Similar to the vibrations of a violin string, the oscillations of black holes do not last long, because black holes are a unique type of celestial object that possesses an event horizon, a single direction highway which once entered, there is no way out. The energy of the gravitational waves propagating around a black hole will likewise dissipate either down to the black-hole horizon by absorption or propagating far away until the waves are far enough for us to detect. Either way, the energy of gravitational waves localised around a black hole is dissipating, and so are the oscillations of the black hole. When the oscillations die down, the distorted black hole becomes a quiet and stationary black hole. The process of a perturbed black hole settling down into a stationary one is called the ringdown phase of a black hole because the process resembles the ringing of musical instruments, such as a bell. Just as a violin string can vibrate in different modes (such as the fundamental mode and overtones), there are also different modes (patterns) of black-hole oscillations. These modes are called the quasinormal modes of black hole, and the oscillation frequencies are called the quasinormal-mode frequencies.

The black-hole ringdown phase is not just of interest to theoretical physics research. It is an actual astrophysical phenomenon which we have detected since the first direct detection of gravitational waves by the Advanced Laser Interferometer Gravitational-Wave Observatory (aLIGO) detectors. The late stage of the first detected gravitational-wave signal, GW150914, clearly shows a ringdown signal emitted by the remnant of a black hole formed by the corresponding black-hole coalescence (see Fig 1). Since then, astrophysicists have been studying the ringdown signal contained in the detected gravitational-wave signals extensively.

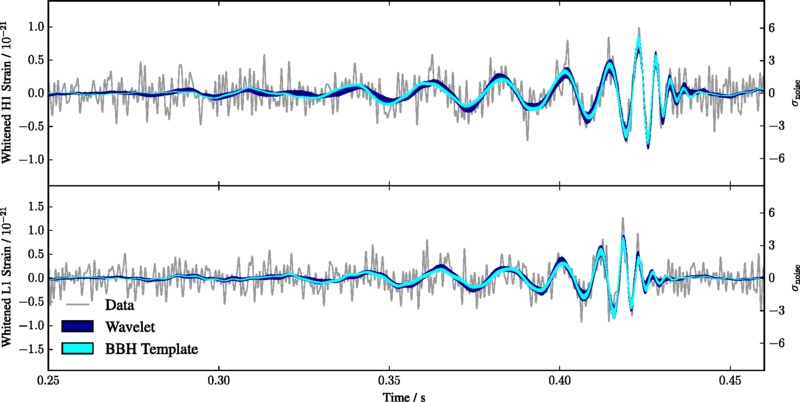
Fig 1: The measured strain of the first gravitational-wave signal detected by the Advanced LIGO detectors. In the late-time phase (on the right of the figure), we see the decaying oscillations of the remnant of a black hole. Figure sourced from [1].

(2) Why should we care about the ringdown phase of black hole?

But why are astrophysicists so keen on analysing and studying the black-hole ringdown phase? In my opinion, the motivations are at least twofold.

Firstly, black-hole ringdown phase is a unique and potent probe for us to answer open questions in fundamental physics. For example, does Einstein's general relativity remain correct in a space-time where gravity is very strong, such as near the event horizon? General relativity is an elegant theory which attributes gravity as a geometric effect of space-time. It also represents our best understanding of the nature of space-time. However, there are some aspects in which general relativity fails to provide a satisfactory explanation, such as the quantum nature of gravity. This shows that general relativity has its shortcomings and requires modifications. But what should be modified? To reveal the limitations of general relativity, scientists have carried out numerous experiments to test the validity of general relativity. Perhaps to the disappointment of some physicists, general relativity has withstood all those tests! However, most of these tests involved relatively weak gravitational field strength because they were carried out on Earth or across the solar system or galaxies. The fact that general relativity passes those tests suggests that if general relativity breaks down, it would only do so in the region where gravity is strong, such as near the black-hole horizon. If general relativity is indeed inaccurate in describing the strong-gravity dynamics of space-time, which governs black-hole oscillations, we will observe dynamics that will be different from the prediction by general relativity. Thus, analysing the ringdown signal is ideal to study the strong-gravity dynamics because the signals are the signatures of the oscillations of the strong-gravity space-time around an astrophysical black hole.

Secondly, through our quest of understanding black-hole oscillations, we will develop rich mathematical tools that can advance research in other scientific fields. To correctly understand the ringdown signals, we must know the oscillatory patterns of black holes well. Mathematically, black-hole oscillations are governed by a set of partial differential equations. In essence, partial differential equations are relations that the partial derivatives involved in the problem have to satisfy. Partial derivatives measure how a variable changes instantaneously as several related variables change [2, 3]. In the context of black-hole ringdown phase, the relevant partial differential equations concern how the oscillation amplitude changes with time and the spatial position around the black hole. Apart from black-hole physics, partial differential equations cropped up in many other fields of science, just to name those closely related to our daily life, for example, stock market, weather forecast, telecommunication, optical fibre, and computational biophysics. In general, partial differential equations are extremely difficult to solve, and those governing black-hole oscillations are no exceptions. To overcome the mathematical challenges, black hole physicists, including me, devote themselves to developing new mathematical techniques to solve complicated partial differential equations. The techniques may also be applied to solve equations arising in other different fields mentioned above.

(3) What can we learn?

Just like an accomplished violinist can name the note upon hearing it, the thickness of the string (is it E, A, C, or G string?), and the status of the violin bridge, a physicist specialised in studying black hole can deduce detailed properties of the black hole by carefully analysing the ringdown signals, such as a ringdown signal consists of decaying oscillations shown in Fig 1. Physically speaking, decaying oscillations can be characterised by two numbers, the frequency, which measures how quickly the oscillations are, and the lifetime, which measures how quickly the oscillations are damped. According to general relativity, the mass and the rotation rate of the black hole completely determine the frequency and lifetime of all oscillatory patterns. For a more massive black hole, the oscillation frequency is smaller; for a more rapidly rotating black hole, the quasinormal mode which we usually detect will last longer. Thus, by quantifying the frequency and the lifetime of the detected quasinormal modes, we can estimate the mass and the rotation rate of the remnant black hole formed. Further to that, we can test if general relativity remains correct in describing the strong-gravity dynamics near the event horizon by measuring the deviation of the frequency and lifetime from the values predicted by general relativity. Thus far, by combining all the ringdown signals measured by the aLIGO and Virgo detectors, physicists have not found any significant deviation of general relativity. Disappointingly or reassuringly, general relativity once again passes this test. But don't be disappointed or reassured for long, these results are essentially limited by the current sensitivity of the detectors. In other words, we find no departure from general relativity that is significantly beyond the measurement uncertainty. The aLIGO and Virgo detectors have started a new observing run, during which the detectors will measure gravitational waves with unprecedented sensitivity. Will we observe the violation of general relativity? Let's hold our breath and stay tuned.

(4) How can we take this forward?

But to be able to correctly and thoroughly interpret these results of testing general relativity through analysing the ringdown signals, we must understand what ringdown signatures will emerge if the black hole does not respect general relativity. Otherwise, even if these violation signatures emerge, we may wrongly attribute them as the signal emitted by an ordinary black hole of different mass and spin. To this end, we need to extensively study the oscillatory patterns of black holes which do not obey general relativity.

As mentioned above, to study black-hole oscillations, we need to solve a set of lengthy partial differential equations. If we take the rotation of black holes into account, which we cannot ignore because astrophysical black holes are rotating rather quickly, the equations are even longer. Exactly how long are they? If you want to print just the shortest partial differential equation on A4-sized paper, it would be at least 56 pages! You need to solve not just one, but at least six of these equations, and many of them are significantly longer. For black holes in general relativity, we can still simplify these lengthy partial differential equations into just one partial differential equation through clever mathematical techniques devised based on the unique geometric properties of black holes in general relativity. But these mathematical techniques do not work for rotating black holes beyond general relativity because these black holes do not possess such geometric properties. Thus, most of the existing mathematical tools are only adequate for studying slowly rotating black holes beyond general relativity. Without knowing the quasinormal modes of rotating black holes beyond general relativity, one cannot consistently and thoroughly test general relativity with the detected ringdown signals.

To remedy this difficulty, in collaboration with Prof Nicolas Yunes and Dr Pratik Wagle at the University of Illinois Urbana-Champaign (UIUC), I am developing a method to tackle these lengthy partial differential equations head-on, without attempting to simplify them at all. Tackling the partial differential equations directly allows us to study the oscillation frequency of rotating black holes under different circumstances, including the violation of general relativity or with dark matter included, because the partial differential equations governing the oscillations of different black holes have the same mathematical structures. Therefore, unlike existing approaches, we can straightforwardly apply our method to compute the quasinormal-mode frequencies of various black holes.

The essence of the method is to express the variables representing black-hole oscillations as a linear combination of spectral functions. Spectral functions are a special type of function that can well approximate other functions as a linear combination, that is, adding or subtracting the spectral functions with suitable weighting constants that we call spectral coefficients. This is a useful property because some functions, such as logarithmic functions, exponential functions, or the solutions of some differential equations, are not elementary. Their mathematical properties are not manifest at first glance. On the other hand, spectral functions are usually easier to manipulate and physicists are familiar with them. Approximating a function by spectral functions often facilitates physics calculations. Just to give you an example, if we would like to well approximate the function, which involves an exponential function, represented by the blue curves in Fig 2, we only need to add up 6 spectral functions to approximate the function extremely well, to the extent that the spectral approximation and the original function almost show no visual differences.

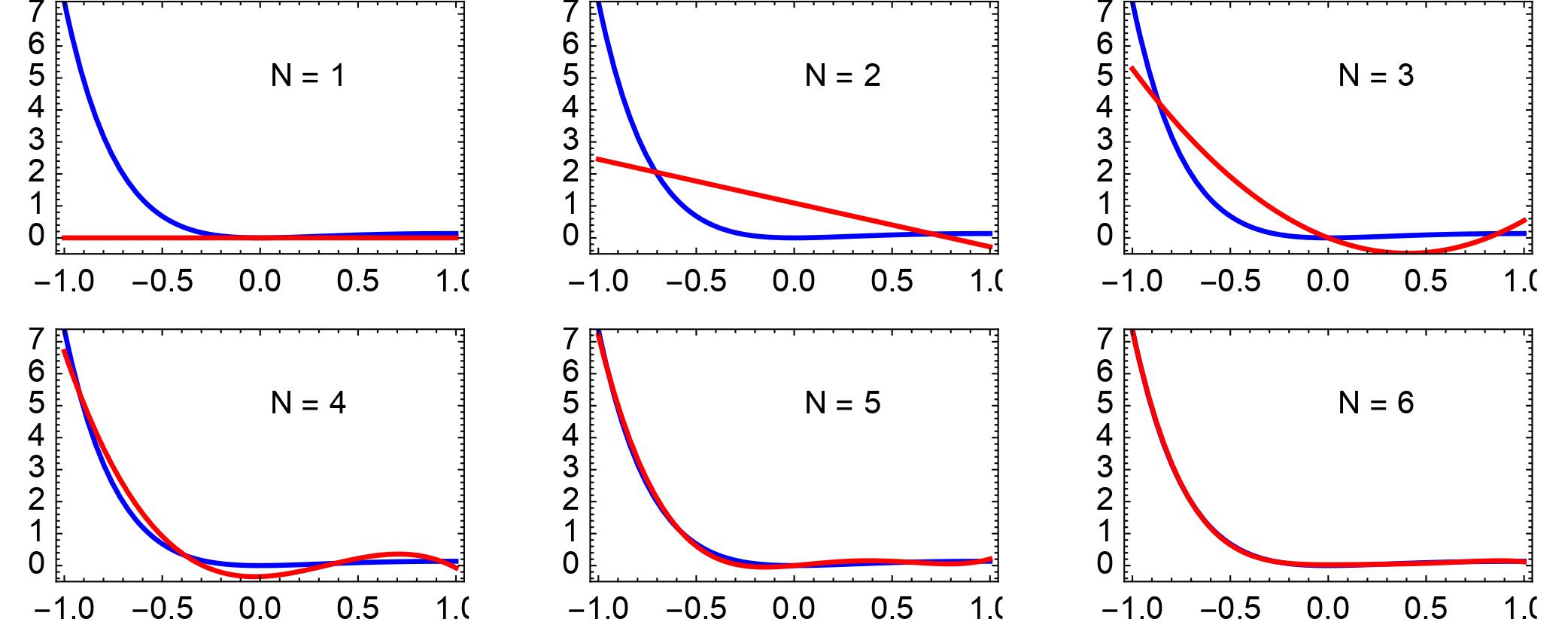
Fig 2: An interesting property of spectral functions is their ability to approximate other functions. For example, if one would like to approximate the function represented by the blue curves in the figure, 6 spectral functions are sufficient to well approximate the functions to the extent that the approximation and original function show almost no visible difference. Figure sourced from [4].

When solving partial differential equations, this ability is an extremely powerful property because if we express the unknown solution as a linear combination of the spectral functions, we can break down the differential equations into algebraic equations governing the spectral coefficients. In general, algebraic equations are much easier to solve than differential equations. As a first step, we applied this spectral method to the partial differential equations concerning the oscillation of non-rotating black holes in general relativity to see if we can recover the known oscillation frequencies. Turns out that the spectral method allows us to compute the frequencies extremely accurately [5], as shown in Fig 3. The blue dots represent the mode frequencies computed using our spectral method, and the black crosses are the known values. If we include sufficient number of spectral functions, we can accurately compute the quasinormal-mode frequencies.

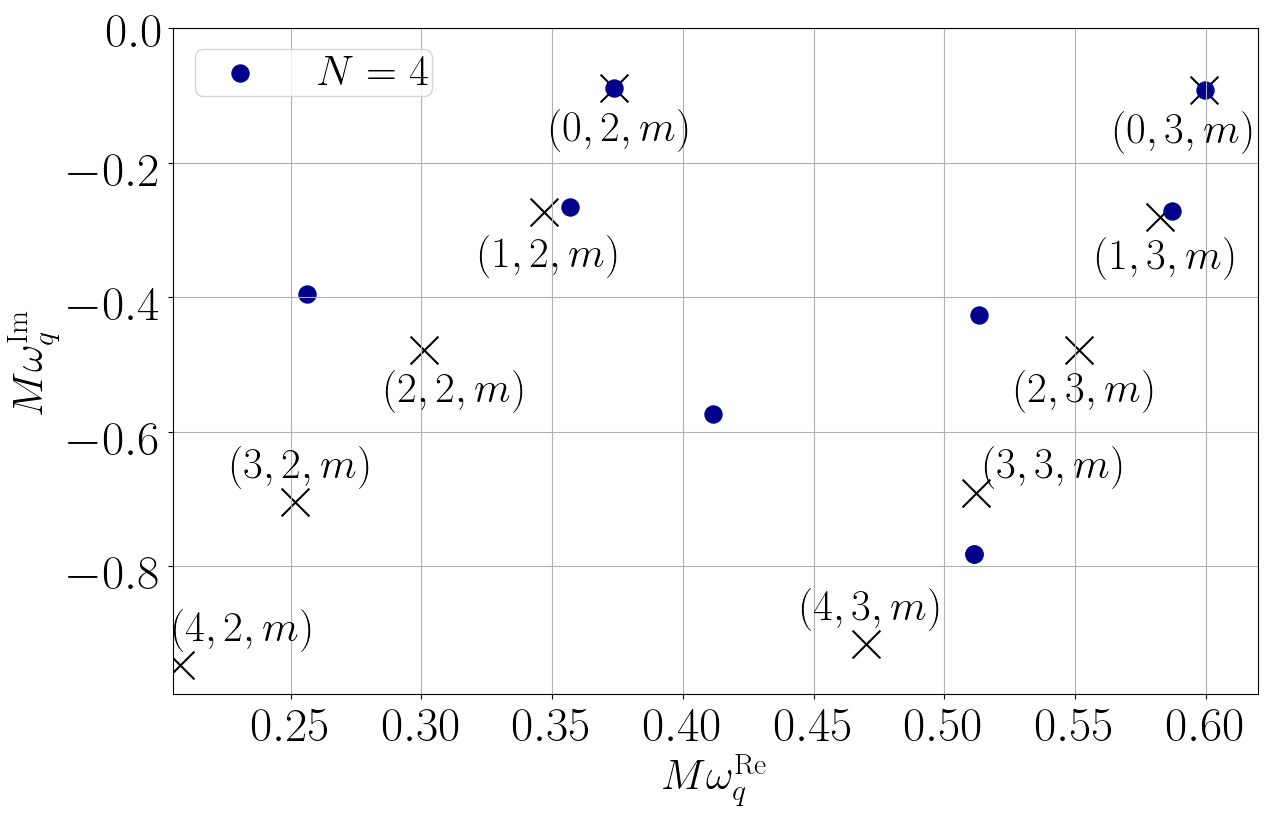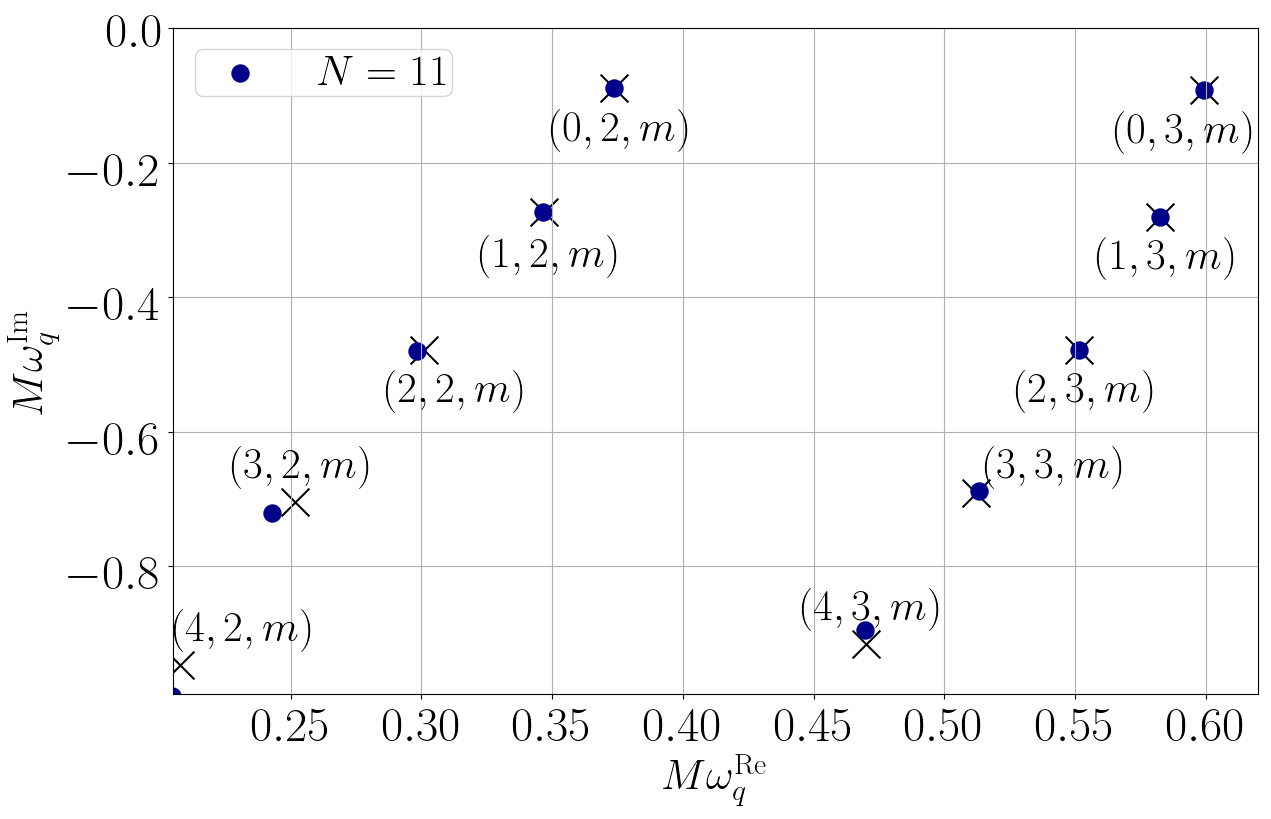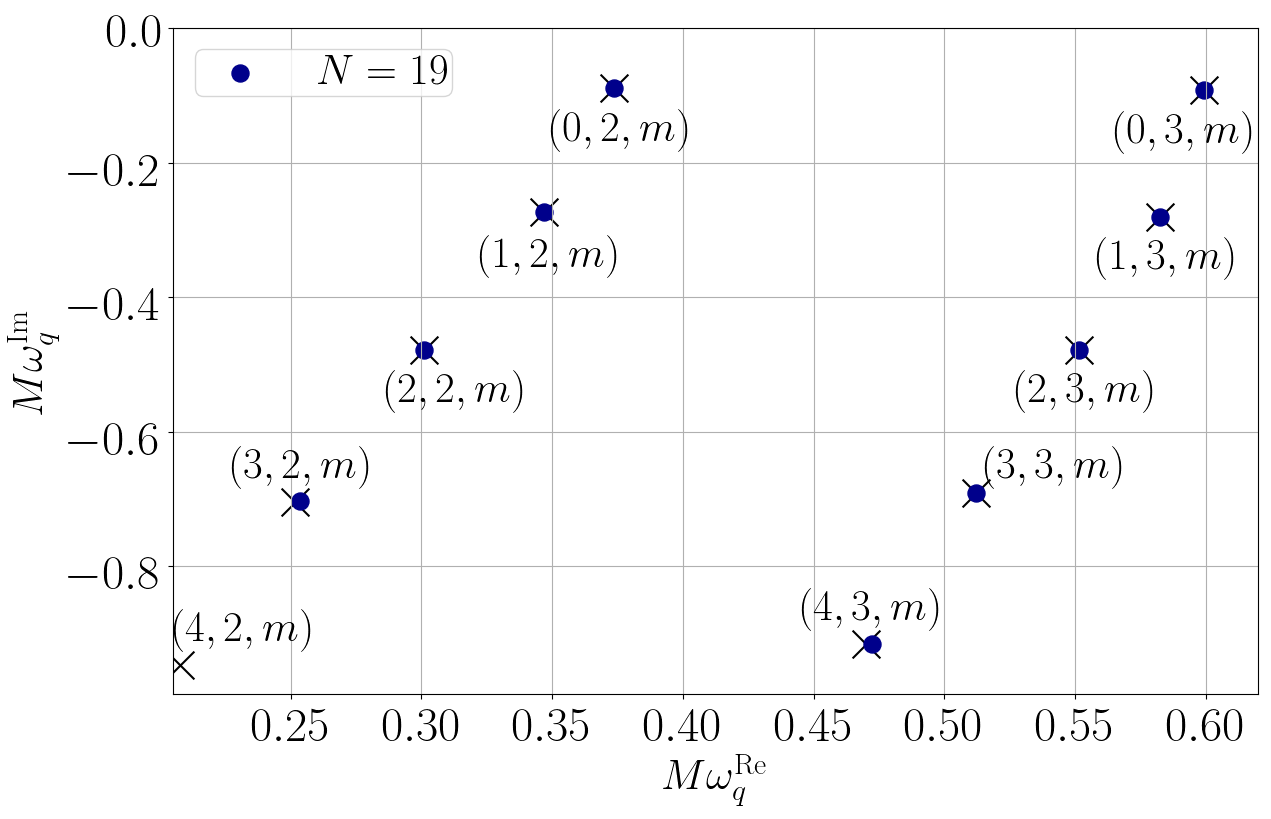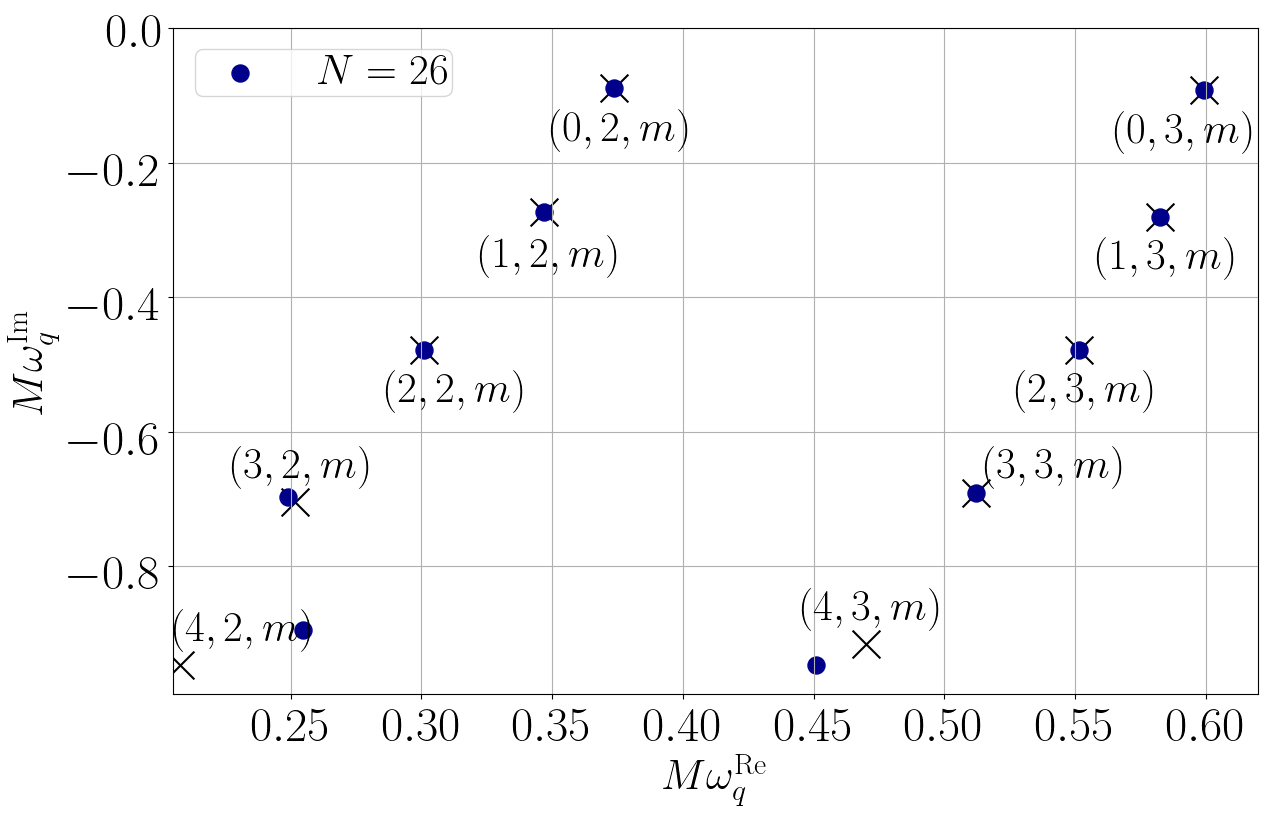
Fig 3: the quasinormal-mode frequencies of a non-rotating black hole in general relativity computed using the spectral method that we develop (blue dots). As the number of spectral functions (N) increases, our results are increasingly consistent with the known values (black crosses). Figure modified from [5].

Now, we are focusing on further developing the method to compute the quasinormal-mode frequencies of the rotating black holes in general relativity. If we can recover the known frequencies accurately, we have validated the spectral method and we are ready to further apply the method to compute the quasinormal-mode frequencies of other black holes which have not been explored or cannot be explored using existing approaches. I have presented some preliminary results in the Focus Group for Young Scientists at the event "Masterminds, Masterclasses 2.0" organised by the Council of the Hong Kong Laureate Forum [6]. More details of the method and results will be covered in a paper which we are currently preparing.

(5) Outlook

Computing the quasinormal-mode frequencies are only the very first step. After obtaining the quasinormal-mode spectra of black holes under different physical conditions, we need to compare the spectra against observation to check the aspects and the extent to which general relativity may need to be amended. All these studies and observation better prepare us to listen and decipher the music produced by perturbed black holes and understand the Universe better through understanding this music.

Further reading

• Chapter 10 of Black hole and space-time wrap, by Prof Kip Throne
• The Perfect Theory: A Century of Geniuses and the Battle over General Relativity, by Prof Pedro G. Ferreira
• Chapter 5 of The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions, by Prof Shing Tung Yau and Prof Steve Nadis

Acknowledgement

The author would like to thank Kirby Ching, Lezhi Lo, and Prof Nicolas Yunes for their feedback on the draft of this article.

References:

1. Properties of the Binary Black Hole Merger GW150914, B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), Phys. Rev. Lett. 116, 241102, https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.116.241102
2. See, e.g. Chapter five of "The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions" by Prof Shing Tung Yau, for a more detailed popular-science introduction about partial differential equations.
3. For the reader who learnt calculus in secondary school, you may recall the concept of derivative, which measures the instantaneous change of a variable with respect to another one. This is called the ordinary derivative because only one independent variable is considered. Partial derivatives consider changes with respect to several independent variables. Hence, partial derivative is a conceptual extension of ordinary derivative.
4. A new approach and code for spinning black holes in modified gravity, by Pedro G. S. Fernandes, David J. Mulryne, https://arxiv.org/abs/2212.07293
5. Spectral Method for the Gravitational Perturbations of Black Holes: Schwarzschild Background Case, Adrian Ka-Wai Chung, Pratik Wagle, Nicolas Yunes, accepted for publication by Physical Review D, https://arxiv.org/abs/2302.11624
6. https://www.youtube.com/watch?v=MDeALFtz-Uc&list=PLkIh51n7eBb2Y5f559D4wTsY2L4GPH2hc&index=2&ab_channel=HongKongLaureateForum

Author:
Mr Adrian Ka-Wai Chung
Postdoc research associate, Department of Physics, University of Illinois Urbana-Champaign
Member, Illinois Center for Advanced Studies of the Universe

October 2023