上年網上遊戲Wordle的風潮席捲全球，大家的社交媒體好一陣子都被綠色、黃色和灰色的方格佔據。你可能見過朋友誇耀自己只猜了三次就已解開當天謎題，也有時會沮喪地抱怨當天只能以「X/6」飲恨作結，未能揭開當天謎底。當我們思考應用甚麼單字開始遊戲時，我們也許會很隨性地把一個五個字母長的任意單字填進空格，但其實這其實是一個科學問題。我們不難意識到有些單字比別的好，對我們稍後的猜測更為有利，譬如選擇「FUZZY」遠比「RAISE」不智，因為前者包括的字母遠比後者冷門。那麼，哪個單字才是能幫我們贏出遊戲的最佳選擇呢？
甚麼是Wordle？
我們假設讀者知道Wordle的運作方式，但如果你不知道的話，以下是懶人包。
Wordle的數據庫包含2,315個由開發者挑選，五個字母長作為答案的單字，也有大概13,000個被系統視為存在的有效單字（裡面除了2,315個作為答案的單字外，還包括許多不常用的單字）[1]。每天程式都會從數據庫抽取一個單字作為當天遊戲的答案。如果你猜的單字包含答案裡有的字母，而該字母位於正確的位置上，該方格將會變為綠色；如字母正確，但位置錯誤，該方格將變為黃色；如答案並沒有包含該字母，方格則會變為灰色。
有用？無用？
解答以上問題前，我們必先量化「有用」這個指標。「有用」的猜測能給我們更多資訊，但我們怎樣量化資訊呢？資訊理論之父Claude Shannon早已在1940年代替我們解決這個問題。
Shannon用以下公式定義資訊：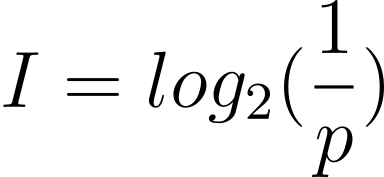
，p為事情發生的概率。你可能會問：為甚麼會是對數函數（logarithm function）呢？回想一下高中時我們學過的對數定律：
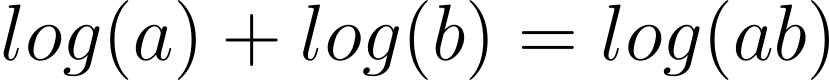，如果有兩件獨立事件，兩者發生的概率分別為p1 和p2，那麼他們兩者都發生的概率會是p1p2，或是
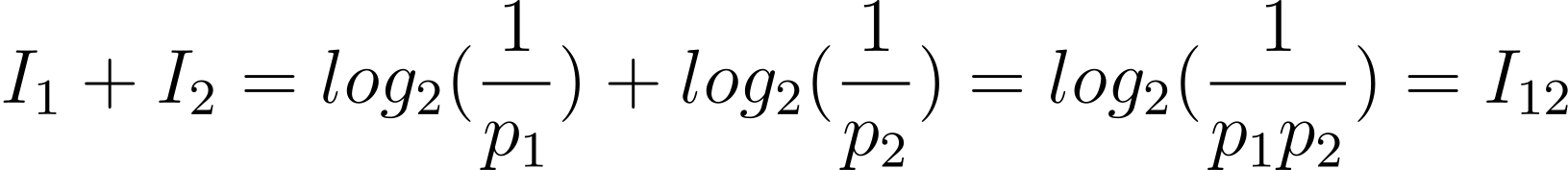
事件發生概率的相乘結構就此保存於公式給出的資訊量裡面。資訊的單位為位元（bit）；在Wordle裡意味著一個單字能把搜尋範圍縮小一半的次數。
「FUZZY」不太可能使我們一撃即中。假如它變出五個灰色方格的話，這些方格給予我們甚麼資訊？
取以上兩個我們用作第一次猜測的單字（「FUZZY」和「RAISE」）作為例子，「F」在英文單字裡出現的概率約為2.2%（表一）[2]，因此它沒有出現的概率為97.8%或0.978。我們可以找出單字中各個字母沒有出現的概率，然後計算出「FUZZY」的總資訊量為0.093位元（註一）：
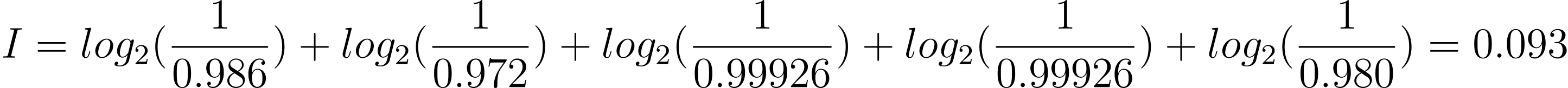
那如果「RAISE」給出五個灰色方格呢？資訊量為：
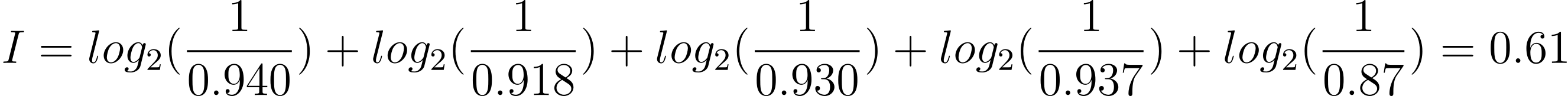
| 字母 | 出現頻率 | 字母 | 出現頻率 |
|---|---|---|---|
| F | 2.2% | R | 6.0% |
| U | 2.8% | A | 8.2% |
| Z | 0.074% | I | 7.0% |
| Y | 2.0% | S | 6.3% |
| E | 13% |
表一：英語裡一些字母的出現頻率（註二）[2]
越不可能發生的事件，一旦發生的話能提供的資訊量就越高。譬如說，一個單字裡可能沒有Z，但並不太可能沒有E，因此欠缺E將能大大縮小我們的搜索範圍。換言之，E變成灰色方格給予我們的資訊比Z變成灰色方格多，因此在同樣取得五個灰色方格的情況下，猜「RAISE」的資訊量比猜「FUZZY」的多。
Shannon熵和單字提供的資訊
以上計算告訴我們猜一個單字時不幸得到五個灰色方格的資訊量，可是我們亦有機會得到不同顏色組合的方格，譬如「灰黃灰灰灰」或是「綠黃灰灰綠」。透過利用全部2,315個答案作分析，對於每個輸入的單字，我們都可以精確計算出得到每個可能顏色組合的概率，以及其相應的資訊量。
考慮所有可能情境後，我們可以計算出一個單字在不同顏色組合下給予我們資訊量的加權平均值。這個平均值名為Shannon熵（Shannon entropy），但與物理學的熵（entropy）並沒有直接關係。有了這指標後，我們就能將所有單字以在第一回合裡可提供的資訊量排序。很多人已經透過這方法分析過Wordle，包括著名的數學YouTube頻道主持Grant Sanderson（3Blue1Brown）。
第一回合應該猜甚麼？
第一回合能提供最多資訊的單字是「SOARE」（5.89位元），一個過時的用字，意思是年幼的鷹 [3]。
有更好的選擇嗎？我們可以考慮接下來的幾回合，畢竟Wordle是個多回合的遊戲，下回合的選擇也很關鍵，因此其中一個有用的思考角度是考慮第一回合選擇的單字如何影響下一回合。假設我們第二回合有能力作出最合適的選擇，在考慮兩回合選擇給出的平均資訊量後，就能計算出第一回合的最佳選擇為「SLANE」，意指愛爾蘭一種園藝用的鏟，首兩回合平均能提供10.04位元的資訊 [3]。
有些讀者可能想以最少的回合勝出Wordle。研究人員在考慮不同第一回合選擇在首兩回合的表現後，篩選了最佳的250個第一回合選擇，然後再用這些選擇各自執行全部2,315場遊戲，以找出每個選擇在遊戲中的實際表現。研究人員發現「SALET」的表現最佳，平均只需3.412回合就能夠勝出遊戲，而「SALET」是一款中世紀的頭盔 [4]。
但實話實說，頭幾名的表現確實不相伯仲。如果你不想以太艱澀的字眼開始遊戲，「CRATE」會是一個好選擇，它在首兩回合能提供10.01位元的資訊，平均以3.434回合就能贏出遊戲，不會比以上提及的艱深字眼相差太遠 [3]。最後，我們並不是建議你背誦所有可能的答案，然後像電腦般分析每一步，但一個明智的選擇也許能幫你以一局美好的遊戲，開展一個美好的早晨。
Footnotes:
- 編按：第二個Z其實也能提供額外資訊；如果猜的單字跟答案均有兩個相同的字母，例如「FUZZY」和「WHIZZ」，兩個Z的方格都會變為黃色或綠色以表示答案包含兩個Z。
- 編按：數值受文本來源（例如一般文件、字典等）影響。表一列出了字母在各類型英文文件中出現的頻率 [2]，但其實更準確估算概率的方法，是找出並採用每個字母出現於《紐約時報》答案列表單字中每一字元的頻率。這裡為了簡單說明概念而採用了一般英語裡的數值，但較準確的估算已經由YouTube頻道主持Grant Sanderson（3Blue1Brown）實驗過 [3]。
參考資料：
- Glaiel, T. (2021, December 30). The mathematically optimal first guess in Wordle. Medium. https://medium.com/@tglaiel/the-mathematically-optimal-first-guess-in-wordle-cbcb03c19b0a
- Lewand, R. E. (2000). Cryptological Mathematics. MAA Press.
- Sanderson, G. (2022). [3Blue1Brown Wordle video source files] [Source code]. GitHub. https://github.com/3b1b/videos/tree/master/_2022/wordle
- Selby, A. (2022, January 19). The best strategies for wordle.. https://sonorouschocolate.com/notes/index.php?title=The_best_strategies_for_Wordle
作者︰蔡蒨珩 香港科技大學《科言》學生編輯
設計︰付一乙 香港科技大學《科言》學生設計師
2023年12月