上年网上游戏Wordle的风潮席卷全球，大家的社交媒体好一阵子都被绿色、黄色和灰色的方格占据。你可能见过朋友夸耀自己只猜了三次就已解开当天谜题，也有时会沮丧地抱怨当天只能以「X/6」饮恨作结，未能揭开当天谜底。当我们思考应用甚么单字开始游戏时，我们也许会很随性地把一个五个字母长的任意单字填进空格，但其实这其实是一个科学问题。我们不难意识到有些单字比别的好，对我们稍后的猜测更为有利，譬如选择「FUZZY」远比「RAISE」不智，因为前者包括的字母远比后者冷门。那么，哪个单字才是能帮我们赢出游戏的最佳选择呢？
甚么是Wordle？
我们假设读者知道Wordle的运作方式，但如果你不知道的话，以下是懒人包。
Wordle的数据库包含2,315个由开发者挑选，五个字母长作为答案的单字，也有大概13,000个被系统视为存在的有效单字（里面除了2,315个作为答案的单字外，还包括许多不常用的单字）[1]。每天程式都会从数据库抽取一个单字作为当天游戏的答案。如果你猜的单字包含答案里有的字母，而该字母位于正确的位置上，该方格将会变为绿色；如字母正确，但位置错误，该方格将变为黄色；如答案并没有包含该字母，方格则会变为灰色。
有用？无用？
解答以上问题前，我们必先量化「有用」这个指标。「有用」的猜测能给我们更多资讯，但我们怎样量化资讯呢？资讯理论之父Claude Shannon早已在1940年代替我们解决这个问题。
Shannon用以下公式定义资讯：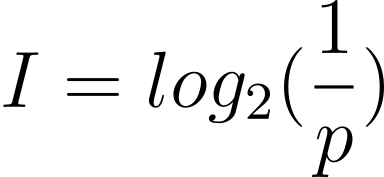
，p为事情发生的概率。你可能会问：为甚么会是对数函数（logarithm function）呢？回想一下高中时我们学过的对数定律：
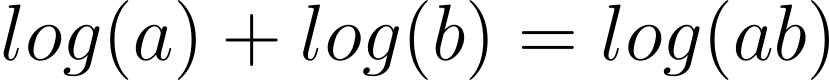，如果有两件独立事件，两者发生的概率分别为p1 和p2，那么他们两者都发生的概率会是p1p2，或是
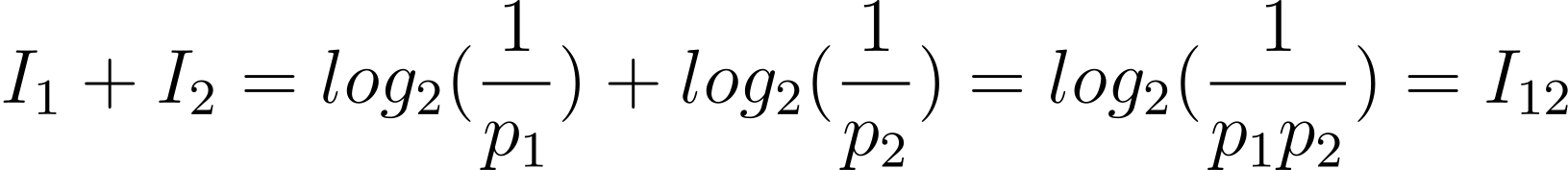
事件发生概率的相乘结构就此保存于公式给出的资讯量里面。资讯的单位为位元（bit）；在Wordle里意味著一个单字能把搜寻范围缩小一半的次数。
「FUZZY」不太可能使我们一撃即中。假如它变出五个灰色方格的话，这些方格给予我们甚么资讯？
取以上两个我们用作第一次猜测的单字（「FUZZY」和「RAISE」）作为例子，「F」在英文单字里出现的概率约为2.2%（表一）[2]，因此它没有出现的概率为97.8%或0.978。我们可以找出单字中各个字母没有出现的概率，然后计算出「FUZZY」的总资讯量为0.093位元（注一）：
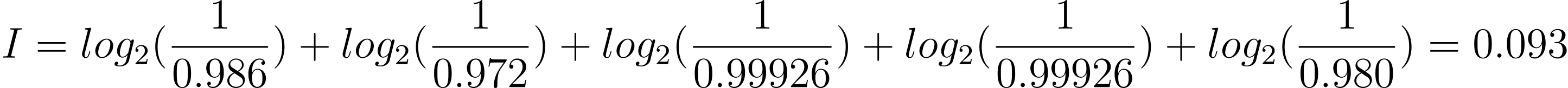
那如果「RAISE」给出五个灰色方格呢？资讯量为：
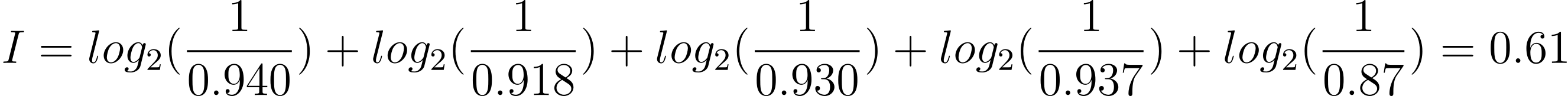
| 字母 | 出现频率 | 字母 | 出现频率 |
|---|---|---|---|
| F | 2.2% | R | 6.0% |
| U | 2.8% | A | 8.2% |
| Z | 0.074% | I | 7.0% |
| Y | 2.0% | S | 6.3% |
| E | 13% |
表一：英语里一些字母的出现频率（注二）[2]
越不可能发生的事件，一旦发生的话能提供的资讯量就越高。譬如说，一个单字里可能没有Z，但并不太可能没有E，因此欠缺E将能大大缩小我们的搜索范围。换言之，E变成灰色方格给予我们的资讯比Z变成灰色方格多，因此在同样取得五个灰色方格的情况下，猜「RAISE」的资讯量比猜「FUZZY」的多。
Shannon熵和单字提供的资讯
以上计算告诉我们猜一个单字时不幸得到五个灰色方格的资讯量，可是我们亦有机会得到不同颜色组合的方格，譬如「灰黄灰灰灰」或是「绿黄灰灰绿」。透过利用全部2,315个答案作分析，对于每个输入的单字，我们都可以精确计算出得到每个可能颜色组合的概率，以及其相应的资讯量。
考虑所有可能情境后，我们可以计算出一个单字在不同颜色组合下给予我们资讯量的加权平均值。这个平均值名为Shannon熵（Shannon entropy），但与物理学的熵（entropy）并没有直接关系。有了这指标后，我们就能将所有单字以在第一回合里可提供的资讯量排序。很多人已经透过这方法分析过Wordle，包括著名的数学YouTube频道主持Grant Sanderson（3Blue1Brown）。
第一回合应该猜甚么？
第一回合能提供最多资讯的单字是「SOARE」（5.89位元），一个过时的用字，意思是年幼的鹰 [3]。
有更好的选择吗？我们可以考虑接下来的几回合，毕竟Wordle是个多回合的游戏，下回合的选择也很关键，因此其中一个有用的思考角度是考虑第一回合选择的单字如何影响下一回合。假设我们第二回合有能力作出最合适的选择，在考虑两回合选择给出的平均资讯量后，就能计算出第一回合的最佳选择为「SLANE」，意指爱尔兰一种园艺用的铲，首两回合平均能提供10.04位元的资讯 [3]。
有些读者可能想以最少的回合胜出Wordle。研究人员在考虑不同第一回合选择在首两回合的表现后，筛选了最佳的250个第一回合选择，然后再用这些选择各自执行全部2,315场游戏，以找出每个选择在游戏中的实际表现。研究人员发现「SALET」的表现最佳，平均只需3.412回合就能够胜出游戏，而「SALET」是一款中世纪的头盔 [4]。
但实话实说，头几名的表现确实不相伯仲。如果你不想以太艰涩的字眼开始游戏，「CRATE」会是一个好选择，它在首两回合能提供10.01位元的资讯，平均以3.434回合就能赢出游戏，不会比以上提及的艰深字眼相差太远 [3]。最后，我们并不是建议你背诵所有可能的答案，然后像电脑般分析每一步，但一个明智的选择也许能帮你以一局美好的游戏，开展一个美好的早晨。
Footnotes:
- 编按：第二个Z其实也能提供额外资讯；如果猜的单字跟答案均有两个相同的字母，例如「FUZZY」和「WHIZZ」，两个Z的方格都会变为黄色或绿色以表示答案包含两个Z。
- 编按：数值受文本来源（例如一般文件、字典等）影响。表一列出了字母在各类型英文文件中出现的频率 [2]，但其实更准确估算概率的方法，是找出并采用每个字母出现于《纽约时报》答案列表单字中每一字元的频率。这里为了简单说明概念而采用了一般英语里的数值，但较准确的估算已经由YouTube频道主持Grant Sanderson（3Blue1Brown）实验过 [3]。
参考资料：
- Glaiel, T. (2021, December 30). The mathematically optimal first guess in Wordle. Medium. https://medium.com/@tglaiel/the-mathematically-optimal-first-guess-in-wordle-cbcb03c19b0a
- Lewand, R. E. (2000). Cryptological Mathematics. MAA Press.
- Sanderson, G. (2022). [3Blue1Brown Wordle video source files] [Source code]. GitHub. https://github.com/3b1b/videos/tree/master/_2022/wordle
- Selby, A. (2022, January 19). The best strategies for wordle.. https://sonorouschocolate.com/notes/index.php?title=The_best_strategies_for_Wordle
作者︰蔡蒨珩 香港科技大学《科言》学生编辑
设计︰付一乙 香港科技大学《科言》学生设计师
2023年12月