用以對新航線所需燃料作出髙效預算的飛機燃料聚類估算模型


摘要：燃料消耗佔飛機的整體營運成本比例達 25%，是航空公司至為重大的決策因素之一。因此，對燃料消耗作出審慎的估算，是航空公司在未來一個財政年度裏確保順利營運的關鍵工作。當航空公司需要估算新航段的總燃料消耗量，而又未能掌握所需數據時，就會出現困難。這便需要有一個強大的參數模型，即使在缺乏相關數據的情況下，也可以借助該模型所描繪的新航線特徵，來作出相關推演工作。為解決這個問題，我們提出一個涉及兩個步驟的方法，來得出一個可用以準確地估算所需飛機燃料的模型。這個構建出來的方法既涉及無監督學習，也涉及一個迴歸模型。對於無監督學習步驟，採用「基於分層密度之噪聲應用空間聚類法」(HDBSCAN)，來對經過主成分分析 (PCA) 方法歸約出的數據進行聚類處理。這個步驟可以在過濾數據中的噪聲後，根據各個航段的主要成分所顯示的基本特徵，自動分類不同的航段。然後，使用多元線性迴歸法 (MLR) 推演出每個聚類的公式。主要成分分析基礎聚類模型被證明優勝於對單一飛機類型採用一通用的模型。對於每個聚類內的現有航線，使用這種方法得出的燃料估算之均方根誤差小於 5%。更重要的是，這個建議使用的方法可用以準確地估算新航線所需的總燃料，總誤差小於 2%，因此能夠解決航空公司燃料估算研究的其中一個現有局限性。

1. 簡介

航空大數據分析在近年以來已經成為一個新興的研究領域 [1]。由於數據的收集和儲存方面有所進步，數據驅動模型或機器學習技術已廣泛地應用於不同的行業，而航空業也不例外 [2]。採用這些技術，能幫助從任何特定的數據集中發現有意義的模式和知識 [3]。先前使用這些技術在航空領域進行的研究之結果，已在航空交通管理 [2]、飛機意外調查 [4]、飛行運作異常 [5]、航空公司飛機性能 [6] 等不同方面得到體現。

由於燃料成本佔航空公司總營運開支的 17-25%，航空公司的一個飛機性能關注點就是燃料消耗量 [7]。正因為燃料預算決定了航空公司在未來一年的盈利能力，因此，具有可靠而且準確的燃料估算模型，對於航空公司來說十分重要。燃料預算取決於耗用的燃料數量及預期的燃料價格。我們明白，燃料價格的波動是決定燃料預算的一個關鍵因素 [8, 9]。但是，燃料價格的預測不在這項研究的範圍之中，而且我們假設各家航空公司都有適當的策略和政策來應對燃料價格的波動問題。在這項研究中，我們聚焦於估算在制定燃料預算時考慮的燃料數量，我們在下文將其稱為燃料消耗估算。為儘量降低由於燃料計劃欠妥造成的損失，有必要實現高度準確的總燃料預測。航空公司花費在燃料上的開支高達數以十億計美元，因此，即使是 1% 的準確度偏差也會涉及大筆的款項。例如某家本地旗艦航空公司在 2021 年錄得總燃料成本 94 億港元（約 12 億美元）[10]；這金額的 1% 已是大約 1,200 萬美元。經與航空公司夥伴討論之後，我們瞭解到，可以假設平均需要的燃料等同於前一年的使用量，從而依靠統計分析，來估算現有航線的總燃料量。對於一些航段接著航段的情況，有可能需要作出輕微的調整，而這種調整通常是根據專家的意見和過往經驗決定的。由於假設個別航班的燃料預測的過高估算及過低估算將會在總計層面上互相抵銷，因此以上做法通常會忽略每次飛行的燃料消耗差異。圖 1 說明這個假設的有效性，當中顯示了在不同航段飛行的特定飛機機型的燃料消耗量的逐年變化。x 軸顯示飛行航段（即始發地與目的地），而 y 軸則顯示標準化的燃料消耗量（請注意，為保密原因，未能顯示實際的燃料消耗數值）。值得注意的是，使用不同的飛機機型時，燃料消耗的分佈可能會有所不同。雖然趨勢看來一致，但由於缺乏數據，在考慮新的航段時，這種統計方法不會奏效，如圖 1 右側所示。


圖 1：不同航段的燃料消耗分佈（2014 年至 2017 年）

在相關文獻裏，存在多種燃料消耗的估計模型，當中包括較簡單的模型以至複雜得多的模型。不同類型的模型針對不同的目的，包括從一次飛行的詳細計算，以至每日到每年營運的較低層次計算。下文載有關於這些模型的概述，以及説明為何它們不適合用來處理正待處理的特定問題。

有些研究聚焦於用盡可能多的細節來表現飛行操作。例如 Lyu 及 Liem [11] 透過就整個飛行任務的輪廓整合出逐個分段的航程公式，開發出一個詳細的飛行任務分析程序。為進行更為逼真的計算，根據實際飛行的數據，對任務輪廓進行參數化。Sun 等人 [12] 開發了一種建基於飛行運動公式的飛行模擬，來估算飛機在飛行期間的燃料流量。此外，Kim 等人 [13] 近期開發了一種數據增強型飛行模擬，當中具有引伸自實際操作數據的一些限制，用以密切地模擬實際運作。Lee 及 Chatterji [14] 則基於飛行運動公式，開發了一個較為複雜的飛行模擬模塊，可以實現更高的準確度，而且起飛重量誤差小於 1%。但是，這些方法都需要掌握到飛行中涉及的複雜和詳細的資料。另外，由於各家航空公司每年都有數百甚至數千次的航班，這些方法的計算成本太高，因此不適合用於進行燃料策劃的工作。

另一方面，一些研究人員則推演出一些較簡單的經驗性模型，這些模型的計算成本要低得多，但卻會犧牲結果的準確性。這種方法更常用以預測總燃料消耗量，而對於每次飛行的燃料預測之準確性則並不重要。O'Kelly [15] 根據經驗，就飛機的大小及飛行距離，推演出一個線性迴歸結果。Yanto 及 Liem [16] 則通過結合低逼真度的Bréguet航程公式和高逼真度的飛行模擬結果，推演出一個多種逼真度的燃料消耗估算方法。此方法特別有利於預測勻速航段並不是主要部分的短途飛行的燃料消耗。在該方法下，為便利進行簡單的總燃料消耗計算，針對每種飛機機型，推演出一個線性迴歸模型，淨載重量及飛行航程都是其輸入因素。Kang 及 Hansen [6] 也開發出聚類專屬的集成學習法，來估算燃料消耗量。他們執行了一個建基於穩定性的 K 均值算法，來對美國的飛行航班進行聚類處理，而結果顯示，飛行航班的燃料表現乃取決於飛行方向。至於為航空公司開發的燃料預測模型，一些研究人員對二氧化碳排放量估算 [17]、燃油裝卸量 [18]、載運成本 [6, 19]、爬升及進場航段的燃料預測 [20] 等進行了研究。但是，據我們所知，現時尚沒有任何研究是聚焦於航空公司燃料預算目的之燃料預測模型建構的。雖然有一些模型可用以預測總燃料消耗量，但正如上文所指，它們都不是專門為航空公司的燃料預算目的而推演出來的。首先，航空公司未必有用於建構這些模型的完全相同的數據集，也就限制了這些主要基於數據的模型的應用。其次，正如上文所指，航空公司燃料預算的準確性乃取決於對燃料消耗量的估算及對燃料價格的預測，而前者就是本文的重點。由於涉及多重因素及不確定性，例如航空運輸需求、航線變更、飛機性能、大氣條件、新航段的引入等，預測未來一年的總燃料消耗量並不容易。舉例而言，若某一月份裏的乘客數量出人意表地增加，將會導致燃料消耗飆升 [21]。雖然以上大多數因素均已經在統計性方法中加以考慮，但正如前文所指，對引入新航段時的總燃料消耗量作出預測，仍然是航空公司面對的一項公開挑戰。因此，航空公司需要有穩健而靈活的燃料消耗估算模型，從而確保能夠審慎地編制全面考慮到各種經營性變化（包括引入新的航段）的燃料預算。本文的其中一項主要貢獻，正是關於如何建構這樣的模型能力。

本文介紹一種新的燃料消耗估算方法，該方法也適用於涉及新航段的燃料預測。有關研究採用了我們的航空公司夥伴分享的實際營運數據。本文提出的方法使用一個借助主成分分析法 (PCA) 的譜理論，透過去除冗餘資料，來降低可用數據的維度。這個降維方法有助於避免過度擬合，並且能夠得出更為穩妥的結果。之後，通過採用無監督聚類算法，對各個主成分作出航班聚類。在確定各個航段的聚類之後，為每個聚類推演出一個線性迴歸模型。當有新的航段出現時，我們設計一種方法，根據航線的特徵，將新航段投入到其中一個聚類。之後，便可以用為所選擇的聚類推演出的線性迴歸函數，來估算該個新聚類的燃料消耗量。對於該方法能否預測新航段的燃料消耗量，將根據其預測準確性和涉及的計算複雜程度，來加以評估。特別是該模型需要滿足航空公司的要求 — 在此情況下，我們參考了我們的航空公司夥伴的要求，亦即要做到總誤差小於 3%。

本文劃分為以下章節。第 2 節描述這次提出的方法，包括當中採用的數據和研究方法。第 3 節介紹該方法得出的結果，並附上其驗證證據，同時還探討將這個方法用於新航段時的表現。第 4 節對這方法和其結果作出總結。

2. 研究方法

我們提出一種系統性的方法，來幫助航空公司估算總燃料消耗量，用於針對現有的和新的航段，制定燃料預算之目的。我們提出的方法包含兩個步驟，步驟 1 是採用「基於分層密度之噪聲應用空間聚類」(HDBSCAN) 算法的無監督學習，步驟 2 是一線性迴歸模型。這個雙重步驟法如圖 2 所示。在步驟 1（以藍色箭頭表示）當中，我們執行 HDBSCAN 算法，根據該算法計算出的密度資料，自動對數據進行分組。圖 2 顯示的聚類數目（三個）只是作為示意，其中每一種顔色的點表示一個獨特的聚類。通過執行 HDBSCAN 算法得出的聚類數目取決於正待處理的具體問題。在我們將數據放入 HDBSCAN 之前，我們使用主成分分析法 (PCA) 減低問題的維度，只保留在認定輸出結果的過程中佔有主導作用的輸入成分。在對數據進行聚類處理後，我們展開步驟 2。在步驟 2（以紅色箭頭表示）當中，我們為每個聚類推演出一個線性迴歸函數，以燃料消耗量作為輸出項目。


圖 2：開發出的用以估算燃料消耗量的雙重步驟法。請注意，此處顯示的三個聚類只是作為示意（該三個聚類以三種不同顏色表示，顔色乃隨意選定）；不同聚類數目的情況均適用這個方法。

在預測特定航段的總燃料消耗量時，我們遵循相同的步驟，首先確定有關航段（不論是現有的還是新的航段）所屬的聚類，然後使用相應的線性迴歸模型來預測燃料消耗量。

2.1. 航空公司所紀錄的飛行營運數據

我們採用了我們的航空公司夥伴提供的營運數據來撰寫本文。有關數據在飛機於地面時（即起飛前和著陸後）進行記錄，儲存於飛行後期信息系統 (PFIS) 之中。因此，這些數據不像以 1 Hz 頻率進行紀錄的快速存取記錄器 (QAR) 數據那樣詳細。表 1 載列了在模型推演過程中考慮的各種輸入因素；這些因素是根據我們與航空公司夥伴旗下從事燃料消耗表現評估和估算工作的工程師互相討論確定的。表現系數特徵 (Perf) 乃指飛機燃料表現相對於最佳狀態的偏差：若是負值的話，表示表現較差，而正值則表示表現較好。

表 1：我們的研究中使用的 PFIS 記錄數據列表



在模型的推演過程中同時使用飛行時間和地面距離資料也許看似多餘。但是，這兩種資料其實是相輔相成的。地面距離資料決定了基本航程資料，而飛行時間則考慮了速度、爬升率和下降率、高度分配、空中交通擁堵期間的等待和盤旋情況等。換言之，飛行時間隱含了飛行期間各種操作變化的資料，因為儘管不同航班可以有相同的始發地及目的地，但沒有飛行路徑是完全一樣的。關於飛行日期特徵，我們只採用月份資料。月份變量 (m) 被轉化為一正弦函數，表示為 ，以捕捉季節性影響。在本研究中，我們使用了採用波音 777-300ER 飛機飛行的 11 個進入或離開香港的始發地與目的地組合或航段，以及採用空中巴士 330-300 飛機飛行的 9 個航段的相關數據。所有具代表性的航段都是根據 2014 至 2017 年期間的航班總數，我們的航空公司夥伴就每種機型營運的頂級航段。在選定具代表性的航段時，短途航班（少於 6 小時）和長途航班（多於 6 小時）[22] 都已考慮在内。採用波音 777-300ER 飛機飛行的航段包括飛往或飛離紐約 (JFK)、多倫多 (YYZ)、洛杉磯 (LAX)、三藩市 (SFO)、溫哥華 (YVR)、倫敦 (LHR)、巴黎 (CDG)、南非豪登省 (JNB)、悉尼 (SYD)、新加坡 (SIN) 和台北 (TPE) 的航班。採用空中巴士 330-300 飛機飛行的航段包括飛往或者飛離墨爾本 (MEL)、珀斯 (PER)、新加坡 (SIN)、吉隆坡 (KUL)、日本關西 (KIX)、上海 (PVG)、馬尼拉 (MNL)、台北 (TPE) 和高雄 (KHH) 的航班。所有這些航段在本文其餘部分都稱為現有航段。

我們也為每一飛機機型選擇了一些「新航段」，來評估我們建構的解決方案在實現預期目標方面的有效性。採用波音 777-300ER 飛行的新航段包括飛往芝加哥 (ORD)、法蘭克福 (FRA)、墨爾本 (MEL) 和曼谷 (BKK) 的航班。採用空中巴士 A330-300 飛行的新航段包括飛往悉尼 (SYD)、檳城 (PEN)、仁川 (ICN) 和曼谷 (BKK) 的航班。請注意，這些其實是由我們的航空公司夥伴營運的現有航段，以確保確有數據可供驗證。但是，這些數據被嚴格用來驗證所建構方法的有效性，並且在訓練過程中被當作「不能看到」。驗證過程將在第 3.3 節裏加以描述。使用這些「新航段」來驗證我們的模型，將會凸顯我們的模型在沒有過往數據之情況下預測總燃料消耗量的有效性。

2.2. 譜分解

主成分分析 (PCA) 是使用至為廣泛的多變量統計性方法，在多個科學領域都有應用 [23]。使用主成分分析法之目的，是從有關數據中提取關鍵的資料，並只保留最為重要的資料，從而減小數據集的規模。有關的主成分 (PC) 乃由多個正交基函數建構而成，這些函數基本上是相關原始基礎的線性組合。使用者可以根據所需的準確度水平和可用的計算預算，來決定代表有關數據集的主成分數目。 當各項數據都處於相似範圍內時，主成分分析法的效用會更好，而這可以通過將數據的平均值居中為零，並將各項數據除以標準偏差來實現。首先，我們對含有 n 個樣本和 m 個特徵的數據 X 進行奇異值分解 (SVD) 分析，將其分解為一個所需的新維度 Nd ，如下面所示：

X = LDRT,

(1)

當中 L∈Rn × Nd包含左奇異向量，R∈R Nd×m包含右奇異向量，而D是由奇異值構成的對角矩陣。請注意，D2是由XTX及XX T的（非零）特徵值構成的對角矩陣。之後，我們就可以找到主成分 (P) 的投影如下：

P = LD = XR.

(2)

關於主成分分析的詳細解釋，可見 [23]。

2.3. 聚類算法

Campello 等人 [24] 提出 HDBSCAN 作為基於密度的噪聲應用空間聚類的擴展。這兩種方法都是使用基於密度的聚類技術得出的。HDBSCAN 透過引入分層聚類方法，可提高聚類結果的表現。在 HDBSCAN 裏，我們無須先行界定聚類的數目，因為該算法會根據密度，自動為每個聚類界定閾值。關於 HDBSCAN 的詳細解釋，可見 [25]。Python 語言編程使用者也可經 https://hdbscan.readthedocs.io/ 訪問所需的程序庫（於 2022 年 10 月 16 日進行訪問）。HDBSCAN 已經成功地應用於軌跡聚類 [26, 27]、運動識別 [28]、文本識別 [29]、氣象預測 [30] 等一些現實問題上。

2.4. 迴歸分析

多變量線性迴歸模型是一個用以表示輸入變量X∈Rn×m及輸出變量Y ∈ ℝn之間關係的一個線性公式 [31]。讓我們將Y及X表示為：


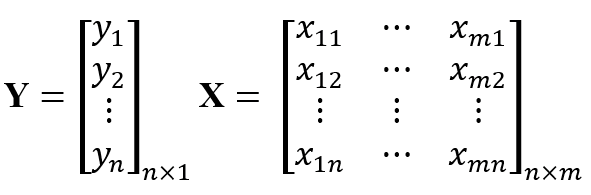
當中n及 m已先行界定；通常 n > m。之後，該個多變量線性迴歸模型可以表示為：

Y = B + XC + ∆,

(4)

當中B ∈ ℝn 含有有關的偏置項，C ∈ ℝm含有該線性公式的系數，而∆ ∈ ℝn 與殘差項目相對應。只需要求解出將 ∆最小化的最小平方，就可以求解出 B及C。這個函數將會用於本文裏的迴歸模型。

3. 結果及討論

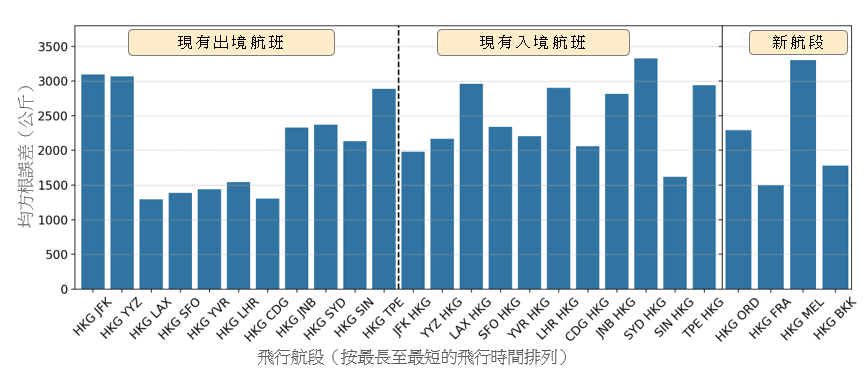
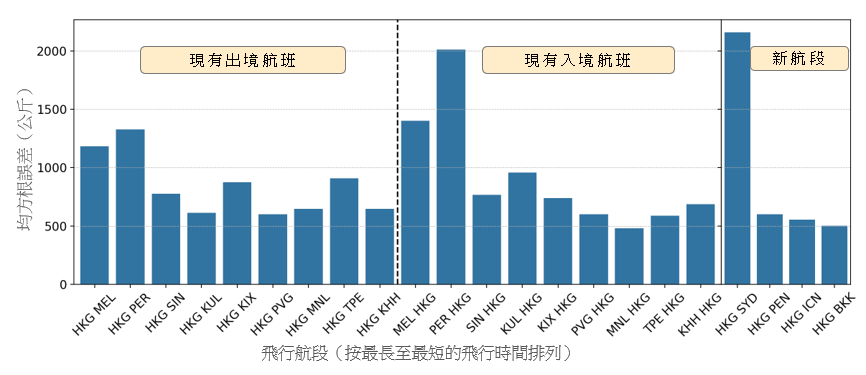
在本節裏，我們會介紹這個構建出的參數化燃料消耗量模型的結果，並將其與現有的一些方法進行比較。為進行比較，我們根據我們之前的工作成果，為每一飛機機型推演出一項線性迴歸 [16]。我們在下文將此模型稱為通用模型。我們把可用數據分為一個訓練集及一個測試集。我們隨機地從每一航段抽出 2014 至 2016 年的 800 個航班樣本作為訓練集，而測試集則包括 2017 年的航班。樣本的數目乃根據每一航段可供採用的最少航班數目而決定。 這個採樣方法有助確保數據在所有航段之間分佈得更加平均，以避免特定航段出現過度擬合的情況。圖 3 顯示就第 2.1 節所列出的現有航段和新航段的測試集得出的通用模型預測表現。x 軸顯示按最長至最短飛行時間排列的航段（包括出境和入境航班），而 y 軸則顯示以公斤為單位的均方根誤差 (RMSE)。通用模型顯示波音 777-300ER 的 RMSE 最高為 3,300 公斤，而空中巴士 330-300 的 RMSE 則最高為 2,000 公斤。在新的航段裏也觀察到類似的誤差範圍。


(a) 波音 777-300ER


(b) 空中巴士 330-300

圖 3：通用模型在測試集得出的預測表現，按現有的出境、入境航班以及新航段分別列出。有關航段乃按最長至最短的飛行時間排列。

根據圖 3 所顯示，這項研究中考慮的兩種飛機機型都沒有觀察到有甚麽趨勢。這表明每個航段都有獨特的燃料消耗表現。因此，有可能需要採用一個針對逐個航段模型，為每一航段推演出一個線性迴歸，以捕捉每一航段的獨特性。可是由於缺乏航段的數據和適當的迴歸模型，這種針對逐一航段的模型不能用來預測新的航段的總燃料消耗量。當這個情況出現時，我們可以選擇另一「相似」的航段作為參照並借用其迴歸函數，但是，這種做法過於主觀。在本文中，我們致力設計一種更系統化的方法，來為新的航段獲取合適的迴歸函數，以消除上述的主觀性。這個稱為主成分分析基礎聚類模型，以及這個我們構建的模型的表現，會在第 3.1 節裏加以解釋。為了進行更全面的比較和模型評估，我們亦利用相同的數據集推斷和演示另一個建基於聚類的線性迴歸模型，即簡單聚類模型。

這個簡單聚類過程完全以國際航空運輸協會 (IATA) 建議的距離 / 飛行時間為基礎 [22]。換言之，這個簡單聚類過程並非遵循任何系統性的方法。表 2 是對這項研究中考慮到的四個迴歸模型的總結。

表 2：用以預測燃料消耗的不同迴歸模型以及各自應用於新航段上的情況之總結



從敏感性分析角度瞭解我們構建的模型，所得出的更深入詳情，將在第 3.2 節作出介紹。要記得，本文提出的方法的其中一個關鍵功能和貢獻，是在沒有數據的情況下對新航段的總燃料消耗量作出預測。我們將在第 3.3 節裏演示以上功能。

3.1. 主成分分析基礎聚類模型

我們所構建出的主成分分析基礎聚類模型，代表著一種更為系統性、更加穩妥的方法，由於它能夠系統性地識別和量化飛行航段的基本特徵，並能夠將這些資料用於模型的推演過程之中，因此這個方法適合用於預測新航段的總燃料消耗量。在本節裏，我們就兩種飛機機型展示我們的方法（如第 2 節所解釋）。波音 777-300ER 飛行航班的聚類結果（步驟 1）見於圖 4a。我們使用「統一流形逼近及投影」(UMAP) 技術來說明二維空間中的數據（https://umap-learn.readthedocs.io/（在 2022 年10 月16日取覽））。當中的兩個軸表示執行投影算法時，數據點在流形中的位置。x 軸是第一個流形軸，y 軸是第二個流形軸。由於在我們的分析中未有使用流形投影的確切值，為簡單起見，未在標繪圖中顯示各個代碼。左圖顯示原始數據，每種顏色代表著一個不同的航段。那些數據是分散的，為每個航段構建了一些小聚類。換言之，該標繪圖並未揭示相似的特徵在不同聚類之間存在著什麽模式。一經我們對那些數據執行主成分分析，就會出現三個截然不同的聚類，就如中間那個圖所顯示那樣（各個數據點仍然按照其所屬航段編以適當顏色）。HDBSCAN 亦自動將這些聚類標示為三個不同的聚類，正如右圖的不同顏色所顯示。可以看到，主成分分析 (PCA) 和 HDBSCAN 將長途航段分成兩批。我們將這兩個長途聚類分為飛往澳洲的長途洲際航班（橙色）（下文稱為 LH-AU B773ER）和飛往美國及歐洲的長途洲際航班（綠色）（下文稱為 LH-US-EU B773ER）。短途航段則歸為一組並名為短途（藍色），下文稱為 SH B773ER。為更好地說明這個聚類方法的結果，這些以顏色顯示的航班在圖 4b 的世界地圖上顯示；新的航段（紅色）亦有在圖中顯示，以便説明。簡單聚類法只會將航班分類為短途和長途航班，而採用我們提出的方法得出的聚類與使用簡單聚類法得出的聚類並不相同。


(a)


(b)

圖 4：對波音 777-300ER 飛機實施建議中方法的視覺化表示。(a) 左圖顯示在實施主成分分析 (PCA) 之前的數據。中圖顯示經過 PCA 程序之後聚類成三組的數據。右圖顯示 HDBSCAN 聚類的結果。(b) 在世界地圖上顯示的航段聚類，包括新的航段。

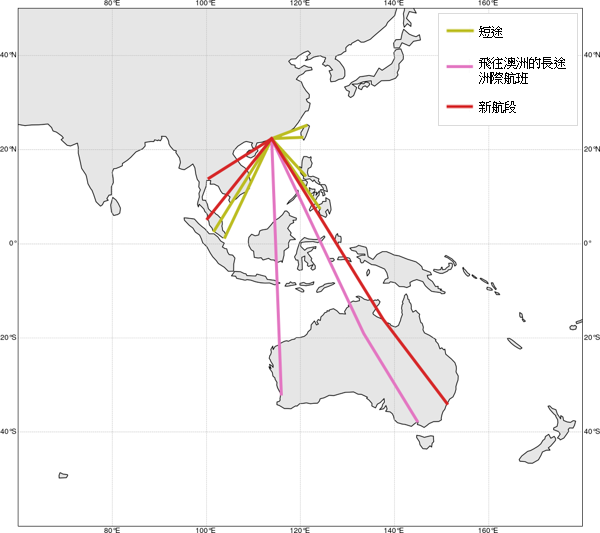
圖 5a 顯示對於空中巴士 330-300 飛行航班的類似聚類結果。有關航段現在分為兩個聚類，就是飛往澳洲的長途洲際航班（粉紅色）(LH-AU A333) 以及短途航班（橄欖色）(SH A333)。與前文一樣，圖 5b 在世界地圖上顯示各個預計飛行航段及其聚類標識。

以上提出的兩個結果顯示，飛往澳洲的洲際航班具備獨有的特點，因為不論採用哪種飛機機型，這些航班都自動與其他航班分開。這表明除了飛行航程外，始發地或目的地的地理位置也會影響到飛行特性以及燃料消耗表現。要記得，澳洲具有與北半球國家相反的季節性特徵。第 3.3 節所介紹的主成分分析基礎聚類結果與簡單聚類結果之間的比較，將會揭示有必要找出與距離相關的特徵之外的飛行特徵。


(a)


(b)

圖 5： 對空中巴士 A330-300 飛機實施建議中方法的視覺化表示。(a) 左圖顯示在實施主成分分析 (PCA) 之前的數據。中圖顯示經過 PCA 程序之後聚類成三組的數據。右圖顯示 HDBSCAN 聚類的結果。(b) 在世界地圖上顯示的航段聚類，包括新的航段。

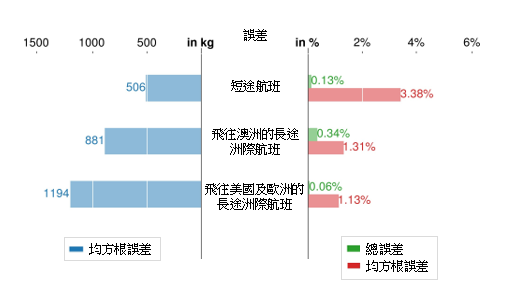
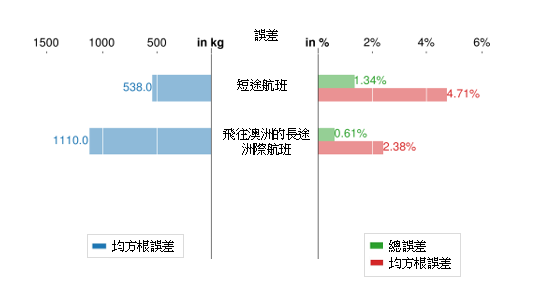
在步驟 2裏，我們要為每個採用 HDBSCAN 定義的聚類推演出其線性迴歸，這些模型在下文中稱為主成分分析基礎聚類模型。我們之前備用的測試集現在用來驗證這些模型；其結果在圖 6 中顯示。該圖以均方根誤差 (RMSE)（以公斤及百分率表示）和總誤差（以百分率表示）的形式，來顯示當中的誤差。所有的 RMSE 值都低於 1,500 公斤及 5%。在以公斤和百分率表示的 RMSE 值當中，都觀察到不同的趨勢。短途航班的以公斤表示的 RMSE 值較小，但以百分率表示的 RMSE 值則比較大。後者是因為據以計算該百分率的燃料消耗參照基準量較低；由於短途航班消耗較少燃料，因此雖然標稱誤差較低，但百分率仍是較高。所有總誤差均低於 1.5%，符合第 1 節所指的航空公司的要求（即低於 3%）。


(a) 波音 777-300ER

(b) 空中巴士 330-300

圖 6：對主成分分析基礎聚類模型進行驗證的結果。左圖顯示以公斤計算的誤差 (RMSE)，右圖則顯示以百分率計算的誤差（總誤差及 RMSE）。

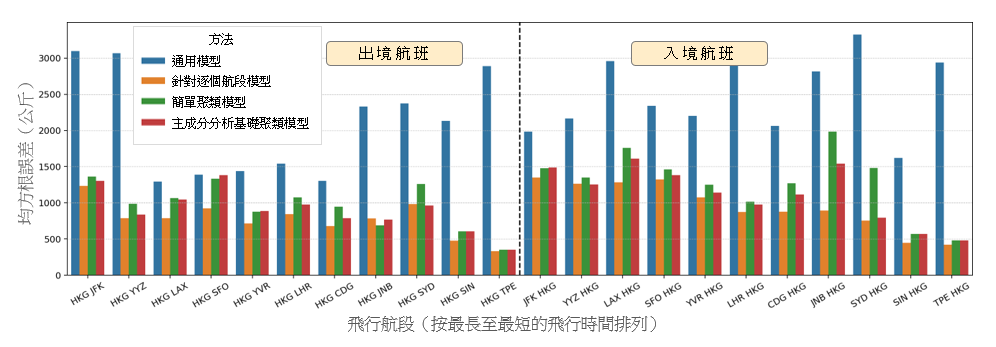
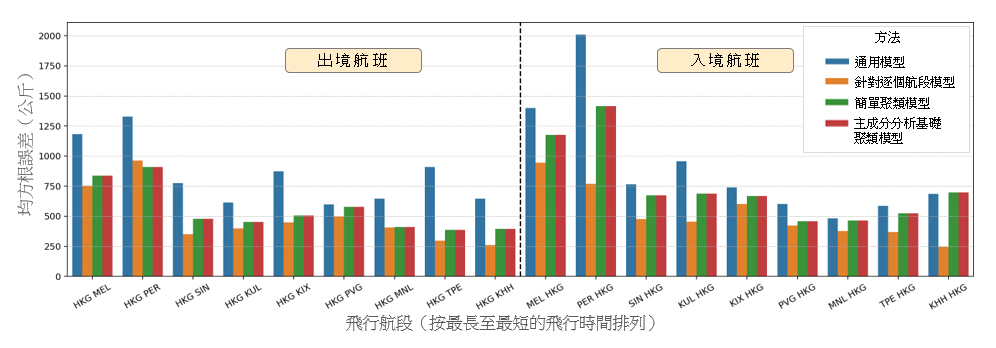
為評估及比較這個新的主成分分析基礎聚類模型與表 2 列出的其他模型（即通用模型、針對逐個航段模型和簡單聚類模型）的表現，我們使用同一個訓練集來訓練所有模型，並計算該個測試集的 RMSE。圖 7 顯示以上四種方法用於該測試集時的表現，x 軸所示的是每個航段（按飛行時間由最長至最短排列），y 軸則顯示相應的 RMSE（以公斤計）。結果證明，對於兩種飛機機型來説，這個新的主成分分析基礎聚類模型的表現都優於通用模型。主成分分析基礎聚類模型在波音 777-300ER 的長途航班上的表現也稍佳於簡單聚類模型。此外，我們的主成分分析基礎聚類模型還有一個額外好處，就是可以用來系統性地預測新航段的總燃料消耗量。第 3.3 節將就此作出演示。這些結果凸顯出，為每一個飛機機型推演一個通用的燃料消耗估算模型的方法，並不足以代表（基於飛行航程和地理位置的）不同的飛行特徵。此外，若為每個航段推演不同的模型的話，則屬於矯枉過正，因為事情會變得更為複雜，卻不會顯著提高估算的準確性。聚類基礎迴歸模型是使用通用模型和針對逐個航段模型這兩者之間的一種折衷做法。與簡單聚類模型相比，使用我們這個主成分分析基礎聚類模型的優點 — 特別是在用於預測新航段的總燃料消耗量方面的優點 — 將於第 3.3 節裏詳述。


(a)


(b)

圖 7：在 (a) 波音 777-300ER 及 (b) 空中巴士 330-300 飛機機型上，四種不同的線性迴歸模型用於每個航段的測試集上的表現

我們還進行了敏感性分析，找出每個聚類之中的主導性輸入因素。有關結果顯示了每一聚類的獨特性，並將在第 3.2 節有所介紹。該項敏感性分析研究的結果，為預測燃料消耗量時需要的重要特徵提出重要的見解。

3.2. 敏感性分析

一般而言，敏感性分析是用來研究每項輸入特徵對於輸出所起的作用 [32]。對於參數性迴歸模型來説，迴歸系數提供了可代表該模型的敏感性的資料。在圖 8 之中，y軸上的是線性迴歸系數，x軸上的是聚類標識符；就每一個輸入因素標繪出一幅圖。在每幅圖中，各條灰色長條表示正待研究的輸入因素的迴歸系數（例如左上圖裏的飛行時間），而主成分分析基礎聚類模型的系數乃以圖 4 和圖 5 當中用來識別各聚類的相同顏色作為識別。

除了 MACLAW 和月份特徵外，每個聚類裏的針對逐個航段的系數都很相似。這顯示這些特徵與其他特徵相比，較不具備代表燃料消耗量的能力。聚類的各個系數證明與各航段的系數的平均值具有相似的大小和方向。但是，我們注意到，（當比較航段的系數和聚類的系數時）某些特徵有不同的大小和方向。要注意，在這情況下，更高的系數不一定意味著對於輸出有更顯著的作用，因為結果仍取決於該特徵的單位和數值。例如，在y = ax 裏，若a = 1000 而x 是以克計算的話，計出的結果並不比 a = 1 而 x 是以公斤計算時大，因為得出的結果並無不同。因此，有需要作進一步分析，以瞭解每個特徵對燃料消耗量所起的作用。

為研究聚類模型裏每一特徵對燃料消耗量所起的作用，我們計算有關的作用平均值，以一百分比率作為該平均值的單位：


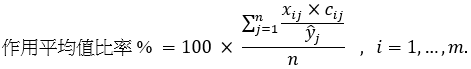
該作用平均值量化了一個迴歸項目xij×cij（與一特定特徵相對應）所需的燃料佔有關航程所需燃料總量的平均比例。該作用平均值與聚類模型系數一起在表 3 裏顯示。粗體數字表示相關特徵對於燃料消耗量的作用程度大於 50%，表示該輸入特徵具有重要性。作用程度小於 10% 的特徵則被認為較不重要。


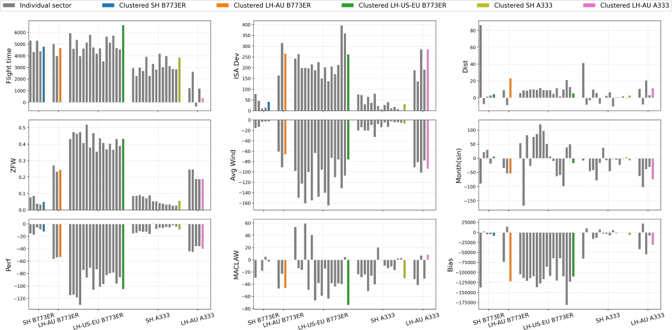
圖 8：在不同的聚類下，兩種不同飛機機型（波音 777-300ER 及空中巴士 330-300）的線性迴歸系數之比較

表 3：為波音 777-300ER 及空中巴士 330-300 推演出的聚類基礎線性迴歸模型之系數。對於燃料總量的作用平均值亦以百分比率形式顯示。

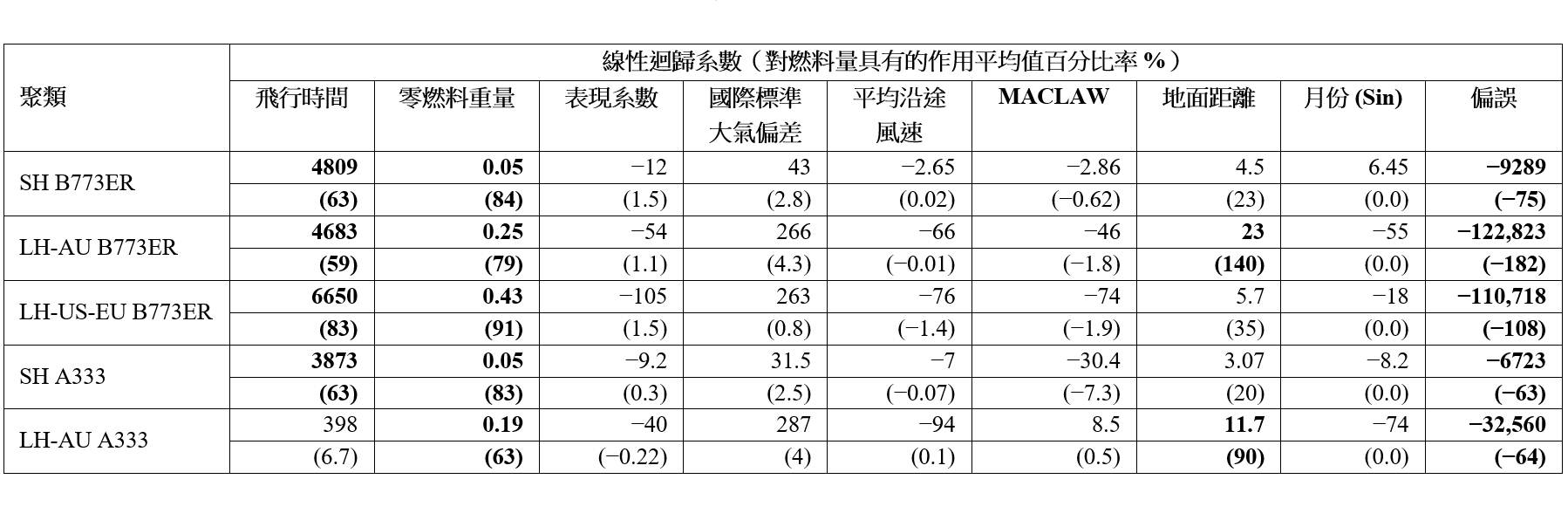
如下文所述，各個具主導性的輸入特徵可以揭示關於各種飛行航段特徵的深刻理解。我們注意到，波音 777-300ER 的燃料消耗主要取決於飛行時間，其次是距離，但長途澳洲航班除外。這項觀察結果也與採用空中巴士 330-300 飛行的長途澳洲航班一致，這表示飛往澳洲的航班往往具有相對更為類似的速度輪廓和一致的飛行路線，而飛行時間有較低主導性的影響正是反映此點。另一項有趣的發現是，不論採用以上哪一個飛機機型飛行的短途航班，零燃料重量都較為可觀。要注意，零燃料重量與決定燃料消耗量的起飛重量有高度的相關性。由於短途航班的巡航範圍較短，但爬升階段佔比更高，以上高度相關性不無道理。爬升過程所消耗的燃料高度取決於飛機的重量，並且對短途航班情況下的總燃料消耗量有可觀的影響作用 [11]。有關結果與我們直覺地認為飛行時間、零燃料重量和距離是最重要的特徵這點脗合。各個重要特徵在不同的聚類之間有不同的系數，這點進一步凸顯出對所有航段使用同一組模型系數的通用模型實在不足以用來代表不同的飛行航段特徵。

3.3. 對於新航段的預測

新航段的定義是沒有任何歷史數據的始發地與目的地組合。為了進行航線規劃和初步分析工作，大部分的航空公司都使用一飛行規劃系統 (FPS)，來取得合理的飛機資料（例如飛機和性能因素）、航線資料（例如飛行時間和距離）以及氣象資料（例如風速等）。但是，所得出的預測並不很準確，因為大部分的操作性變化都沒有被顧及到。故此，航空公司不能單單倚賴 FPS 的預測來估算新航段的燃料消耗。

在這次研究裏，除了用以訓練有關模型的航段外，我們還借用一些現有航段來模擬新的航段，詳如第 2 節所述。通過此舉，我們可以根據可用的燃料消耗資料適當地驗證有關模型。驗證有關模型的方法，是依循均方根偏差 (RMSE) 和總誤差在第 3.1 節中的定義和用法，評估均方根偏差 (RMSE) 和總誤差。此外，我們也將採用主成分分析基礎聚類模型獲得的結果，與採用通用模型和簡單聚類模型得出的結果進行了比較。

以我們的主成分分析基礎聚類模型預測燃料消耗量時，第一個步驟是為有關的新航段界定適當的聚類。在妥善地界定每個聚類內的航段特徵之後（例如飛往南半球的長途航班、飛往北半球的長途航班、短途航班等），便能夠合理地以人工方式編配有關聚類。例如，由於香港至墨爾本 (HKG-MEL) 與香港至悉尼 (HKG-SYD) 相似，因此可以歸類為長途澳洲聚類。一經界定聚類，我們就可以簡單地使用以飛行規劃系統 (FPS) 生成的新航段的相關輸入，來運用相應的迴歸模型。圖 9 顯示對前述兩種飛機機型運用三種不同的模型（即通用模型、簡單聚類模型和主成分分析基礎聚類模型）之結果比較。結果顯示，與通用模型相比，使用聚類模型具有明顯的優勢。這就表示通用模型並不足以代表飛機營運中涉及的航段變化。在此項研究中，與空中巴士 330-300 相比（空中巴士只有長途和短途聚類），波音 777-300ER 的航班具有更為多樣化的航段（基於主成分分析 (PCA)，波音 777-300ER 的航班得出三個聚類）。要記得，簡單聚類模型只是根據飛行航程（短途或長途）來決定，而並不區分始發地 / 目的地的地理方向。因此，主成分分析基礎模型和簡單聚類模型就空中巴士 330-300 的航班得出相同的預測結果和有相同的準確性也就不足為奇。對「新的」香港至墨爾本 (HKG-MEL) 航段採用主成分分析基礎聚類模型預測其燃料消耗量時，可以清楚地觀察到誤差指標有所減少，這個主成分分析基礎聚類模型的優越性可見一斑。上述誤差指標的減少，是因為主成分分析基礎聚類程序可以自動識別出不同的長途航班（美國和歐洲至澳洲）之間的不同特徵。在這項研究中，由於數據所限，在證明我們構建的方法的優點時存在限制。當在訓練過程和聚類過程之中考慮更多的航段（而且各航段有更多的特徵差別）時，採用系統性和自動的主成分分析基礎聚類方法的好處將會更為明顯。

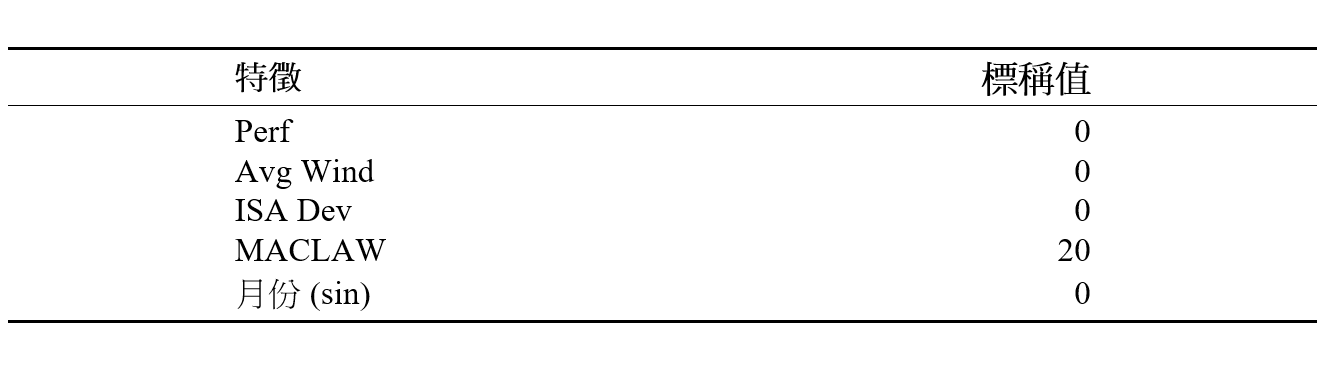
人們或會懷疑，當可以獲得的數據（可變因素的數目）並不如航空公司可以提供的那麽多時，我們提出的方法是否適用。生成的飛行規劃系統 (FPS) 輸入項目往往屬於機密，並僅給予航空公司使用。因此，我們還推演出只由三個輸入項目（即飛行時間、零燃料重量和飛行距構成的簡化版模型。在敏感性分析裏，這三個輸入項目是最主要的特徵，如表 3 所示。要記得，飛行時間和飛行距離特徵是互補的；由於飛行軌跡具有三維性質，飛行時間和飛行距離這兩者之間的關係不能簡單地用速率來描述。由於飛機的速度、高度、空中交通擁擠和中斷情況各有不同，兩個航班可以飛行相同的距離，但所需的飛行時間卻會有分別。為進行比較，我們將具有較少特徵的模型稱為簡化版通用模型和簡化版主成分分 析基礎聚類模型。這些簡化版模型採用表 3 中列出的相同迴歸系數，但只考慮偏誤項目和從航班資料獲得的三個輸入項目，而其餘的輸入項目則設置為表 4 所列出的標稱值。

請注意，對波音 777-300ER 和空中巴士 330-300 這兩種機型均採用這些標稱值。這是為模擬可以採用參數性模型、但使用者無法取得詳細的航班資料輸入項目的情況。之後，我們採用簡化版通用模型和主成分分析基礎聚類模型的表現，來分析原有的通用模型和主成分分析基礎聚類模型；得出結果如圖 10 所示。


(a)

(b)

圖 9：在 (a) 波音 777-300ER 及 (b) 空中巴士 330-300 飛機機型上，分別採用通用模型、簡單聚類模型及主成分分析基礎聚類模型來預測新航段的燃料消耗的模型表現比較。上圖顯示按公斤計的均方根誤差 (RMSE) 值；中圖顯示按百分率計的均方根誤差 (RMSE) 值；下圖則顯示按百分率計的總誤差。


(a)

(b)

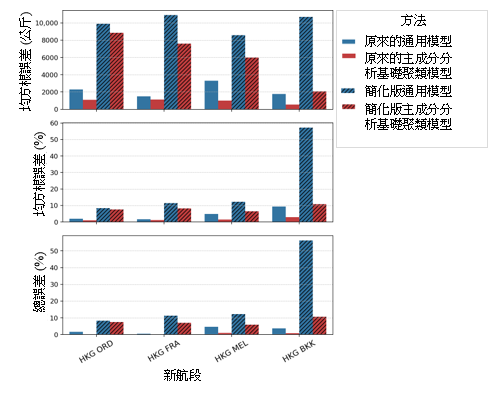
圖 10：在 (a) 波音 777-300ER 及 (b)空中巴士 330-300 飛機機型上，分別採用原來的通用模型、原來的主成分分析基礎聚類模型、簡化版通用模型、簡化版主成分分析基礎聚類模型來預測新航段的燃料消耗的模型表現比較。上圖顯示按公斤計的均方根誤差 (RMSE) 值；中圖顯示按百分率計的均方根誤差 (RMSE) 值；下圖則顯示按百分率計的總誤差。

表 4：對波音 777-300ER 和空中巴士 330-300 採用簡化版通用模型和簡化版主成分分析基礎聚類模型時，被「排除在外」的輸入因素的標稱值

結果顯示，簡化版的主成分分析基礎聚類模型仍具有可以接受的準確度。雖然所有簡化版通用模型都顯示出比相應的簡化版主成分分析基礎模型有較高的誤差，但圖 10a 顯示，當這兩種模型運用於香港至曼谷 (HKG-BKK) 航段時，兩者之間的準確性差異明顯更大。進一步調查發覺，實際平均表現因數 (-16%) 與假定標稱值（如表 4 所示的 0%）之間的偏差是導致有上述更大誤差的部分原因。通用模型的 Perf 系數是 -84，但主成分分析基礎聚類模型的 Perf 系數卻是 -12（如表 3 所示）。故此，通用模型和簡化版通用模型之間的預測差異 (-84 × Perf ) 比主成分分析基礎聚類模型和其簡化版之間的預測差異 (-12 × Perf ) 更為巨大。圖 11 說明了為簡化版模型選擇適當的標稱值的重要性。當中顯示，當標稱的 Perf 值更為接近實際平均值時，均方根誤差 (RMSE) 便會降低。請注意，由於其他航段的平均 Perf 值（範圍在 -5% 和 5% 之間）較接近假定的標稱值，其他航段並沒有觀察到大幅度的差異。


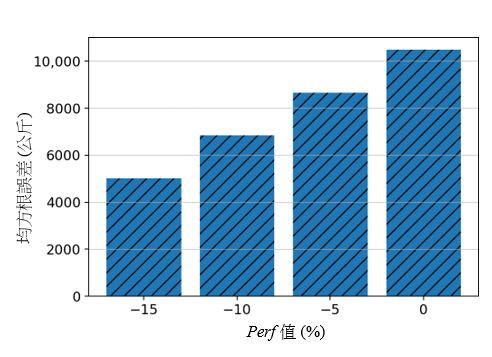
圖 11：在不同 Perf 標稱值情況下，對香港至曼谷 (HKG-BKK) 航段運用簡化版通用模型時的均方根誤差 (RMSE) 值。這顯示當標稱 Perf 值更為接近實際平均值 (-16) 時，準確度將會提高。

以上結果顯示，即使欠缺某些真實的特徵值，但我們建構的主成分分析基礎聚類模型很一致地具有優於通用模型的表現。此外，這個簡化版的主成分分析基礎聚類模型更容易地為其他使用者所採用，因為只需要有基本的航班資料作為輸入項目即可。

4. 結論

我們展示了一種用以估算燃料消耗量的新方法。由於我們採用的資料和數據乃航空公司可以具體取得的數據，因此該方法對於航空公司的預算編制應很有用。我們的其中一個主要目標是構建一種方法，來系統地預測除現有航段外的新航段總燃料消耗量，從而設法解決現有模型的局限性。我們具體上構建了一個主成分分析基礎聚類模型，並對波音 777-300ER 及空中巴士 330-300 這兩種飛機機型運用了這個構建的方法。結果顯示，由於不同的飛機機型有不同的燃料表現特性，故此有必要為每種飛機機型推演出專屬的燃料模型；這些結果符合我們之前的觀察 [16]。

此外，我們的研究顯示，對每種飛機機型採用一個通用的線性迴歸模型（這種做法在其他燃料模型中普遍採用）是不足夠的。這是由於在不同航段裏的燃料表現並不相同。換言之，燃料消耗量不單單取決於飛機航程，還取決於任務概況和航班涉及的地點。由於不同類型航班有不同的主要階段，故此短途和長途航班具有不同的燃料消耗特性。在短途航班的燃料消耗量當中，爬升階段佔主要部分。相反，在長途航班的燃料消耗量當中，巡航階段佔主要部分 [11]。因此，在推演模型時需要考慮到這項差異，而我們在推演主成分分析基礎聚類模型時己經考慮到這點。此外，若使用聚類基礎迴歸模型，便無需推演逐一航段的燃料消耗模型，省卻當中涉及的麻煩。

我們並不採用以人手方式將各個航段劃為短途或者長途航班，而是使用 HDBSCAN 作為無監督聚類方法，建構出一個主成分分析基礎聚類方法。使用主成分分析法，有助揭示原本在單單考慮原始的輸入因素時不同航段裏一些並不明顯的特徵。以波音777-300ER 飛行的航段被聚類為三個組別，分別是短途航班、長途澳洲航班以及長途美國及歐洲航班。與此同時，以空中巴士 330-300 飛行的航段則聚類為兩個組別，分別是短途航班和長途澳洲航班。通過對每一聚類作出清晰的特徵描述，便可以在缺乏數據的情況下，輕易地將新的航段投入到其中一個聚類。在這項研究中，由於我們的航空公司夥伴分享的數據較為有限，因此我們只考慮了少數幾個航段。當涉及更多航段時，聚類程序有可能會更加複雜，並且如果有關的聚類基礎線性迴歸的準確度不能符合要求，則可能需要進行分層的聚類。

我們已展示了採用主成分分析基礎聚類模型來估算現有航段和新航段的燃料消耗量之好處。這個模型在計算效率、有效性和直觀性之間作出平衡取捨。由於這個模型具有參數化的性質，其他人即使無法取得用於構建模型的原始數據集，也無礙使用該模型，因此這個模型具備更為廣泛的適用性。這次建構的主成分分析基礎聚類模型的準確性，乃通過評估均方根誤差 (RMSE) 和總誤差來加以驗證。結果所有的 RMSE 值均低於 5%，所有的總誤差均低於 2%，當中均已包括新航段的燃料消耗量預測。這樣的預測能力符合我們的航空公司夥伴的要求，亦即總誤差要小於 3%。我們還證明了簡化版主成分分析基礎聚類模型（只考慮了三個關鍵的輸入項目而對其他因素發配標稱值）儘管未有包含一些資料，但仍然提供充分的準確性。當使用者無法取得除飛行時間、零燃料重量和飛行距離以外的飛行資料時，這不失為一個實用、有助益的方法。

我們這個新的燃料估算方法結果令人鼓舞。由於我們這個解決方案具有以數據為基礎的性質，同一方法可以在對應不同飛機機型、燃料種類、航段、航空公司等的不同數據集上運用。得出的模型可用以進行比較，從而進一步豐富我們的燃料消耗量估算研究，以及有助更深入瞭解飛機燃料表現。

各作者負責部分： 概念化：J.Y. 及 R.P.L.；數據治理：J.Y.；方法學：J.Y.；驗證：J.Y.；撰寫 — 準備初稿：J.Y.；撰寫 — 審閲及編輯：R.P.L.；監督：R.P.L.。所有作者均已閱讀並同意採用此手稿的出版版本。

資金：此項研究並無得到外界資助。

數據可用性聲明：不適用

鳴謝：此項研究中使用的數據，乃由國泰航空公司根據該公司與香港科技大學機械及航空航天工程學系訂立的數據合作協議提供，作者謹此向國泰航空公司致以衷心謝意！作者亦由衷感謝 Steve Yip 先生在此項研究中參與討論並提供寳貴建議。

利益衝突：作者聲明並無利益衝突情況。

縮略語：
本文使用以下縮略語：

HDBSCAN 基於分層密度之噪聲應用空間聚類法
PCA 主成分分析
PFIS 飛行後期信息系統
QAR 快速存取記錄器
RMSE 均方根誤差
UMAP 統一流形逼近及投影技術

參考資料：


  1. Akerkar, R. Analytics on Big Aviation Data: Turning Data into Insights. Int. J. Comput. Sci. Appl. 2014, 11, 116–127.
  2. Li, M.Z.; Ryerson, M.S. Reviewing the DATAS of aviation research data: Diversity, availability, tractability, applicability, and sources. J. Air Transp. Manag. 2019, 75, 111–130. [CrossRef]
  3. Burmester, G.; Ma, H.; Steinmetz, D.; Hartmannn, S. Big Data and Data Analytics in Aviation. In Advances in Aeronautical Informatics; Durak, U., Becker, J., Hartmann, S., Voros, N., Eds.; Springer: Cham, Switzerland, 2018. [CrossRef]
  4. Christopher, A.B.A.; Vivekanandam, V.S.; Anderson, A.B.A.; Markkandeyan, S.; Sivakumar, V. Large-scale data analysis on aviation accident database using different data mining techniques. Aeronaut. J. 2016, 120, 1849–1866. [CrossRef]
  5. Li, L.; Das, S.; Hansman, R.J.; Palacios, R.; Srivastava, A.N. Analysis of flight data using clustering techniques for detecting abnormal operations. J. Aerosp. Inf. Syst. 2015, 12, 587–298. [CrossRef]
  6. Kang, L.; Hansen, M. Improving airline fuel efficiency via fuel burn prediction and uncertainty estimation. Transp. Research Part C 2018, 97, 128–146. [CrossRef]
  7. EUROCONTROL. Fuel Tankering in European Skies: Economic Benefits and Environmental Impact. Aviation Intelligence Unit—Think Paper, June 2019. Available online: https://www.eurocontrol.int/publication/fuel-tankering-european-skies-economic-benefits-and-environmental-impact/ (accessed on 16 October 2022).
  8. Kang, W.; Perez de Gracia, F.; Ratti, R.A. Economic uncertainty, oil prices, hedging and U.S. stock returns of the airline industry. N. Am. J. Econ. Financ. 2021, 57, 101388. [CrossRef]
  9. Horobet, A.; Zlatea, M.L.E.; Belascu, L.; Dumitrescu, D.G. Oil price volatility and airlines' stock returns: evidence from the global aviation industry. J. Bus. Econ. Manag. 2022, 23, 284–304. [CrossRef]
  10. Cathay Pacific Airways Limited. Annual Report 2021; Cathay Pacific Airways Limited: Hong Kong, China, 2021.
  11. Lyu, Y.; Liem, R.P. Flight performance analysis with data-driven mission parameterization: Mapping flight operational data to aircraft performance analysis. Transp. Eng. 2020, 2, 100035. [CrossRef]
  12. Sun, J.; Hoekstra, J.M.; Ellerbroek, J. OpenAP: An Open-Source Aircraft Performance Model for Air Transportation Studies and Simulations. Aerospace 2020, 7, 104 . [CrossRef]
  13. 13. Kim, D.; Seth, A.; Liem, R.P. Data-enhanced dynamic flight simulations for flight performance analysis. Aerosp. Sci. Technol. 2022, 121, 107357. [CrossRef]
  14. Lee, H.T.; Chatterji, G.B. Closed-form takeoff weight estimation model for air transportation simulation. In Proceedings of the 10th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Fort Worth, TX, USA, 13–15 September 2010.
  15. 15. O'Kelly, M.E. Fuel burn and environmental implications of airline hub networks. Transp. Res. Part D 2012, 17, 555–567. [CrossRef]
  16. 16. Yanto, J.; Liem, R.P. Aircraft fuel burn performance study: A data-enhanced modeling approach. Transp. Res. Part D Transp. Environ. 2018, 65, 574–595. [CrossRef]
  17. Seymour, K.; Held, M.; Georges, G.; Boulouchos, K. Fuel Estimation in Air Transportation: Modeling global fuel consumption for commercial aviation. Transp. Res. Part D Transp. Environ. 2020, 88, 102528. [CrossRef]
  18. I˙lker Guven Yilmaz.; Kartal, E.; Özen, Z.; Gulsecen, S. Prediction of Fuel Tankering in AviationIndustry with Machine Learning Algorithms. J. Aeronaut. Space Technol. 2021, 14, 19–34.
  19. Ryerson, M.S.; Hansen, M.; Hao, L.; Seelhorst, M. Landing on empty: Estimating the benefits from reducing fuel uplift in US Civil Aviation. Environ. Res. Lett. 2015, 10, 094002. [CrossRef]
  20. Chati, Y.S.; Balakrishnan, H. Data-Driven Modeling of Aircraft Engine Fuel Burn in Climb Out and Approach. Transp. Res. Rec. 2018, 2672, 29, 1–11. [CrossRef]
  21. Litingtung, S.; Consultants, S.M. White Paper: The Fuel Budgeting Complexities. Available online: https://www.aircraftit.com/articles/white-paper-the-fuel-budgeting-complexities/ (accessed on 3 October 2022).
  22. IATA. Air Transport and Travel Industry IATA Edifact and Xml Codeset Version 20.2. Available online: https://cdn.document360.io/4b1f93b7-f7b8-4ebb-81be-c17af837a94f/Images/Documentation/Code%20set%20Directory%2020.2.pdf (accessed on 16 October 2022).
  23. Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [CrossRef]
  24. Campello, R.J.G.B.; Moulavi, D.; Sander, J. Density-Based Clustering Based on Hierarchical Density Estimates. In Proceedings of the 17th Pacific-Asia Conference, PAKDD 2013, Gold Coast, Australia, 14–17 April 2013; Pei, J., Tseng, V.S., Cao, L., Motoda, H., Xu, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 160–172.
  25. McInnes, L.; Healy, J. Accelerated Hierarchical Density Based Clustering. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 33–42. [CrossRef]
  26. Maulydiana, S.F. Probabilistic Approach in Flight Trajectory Modeling for Fast and Efficient Noise Contour Generation. Master's Thesis, The Hong Kong University of Science and Technology, Hong Kong, China, 2019. [CrossRef]
  27. Wang, L.; Chen, P.; Chen, L.; Mou, J. Ship AIS Trajectory Clustering: An HDBSCAN-Based Approach. J. Mar. Sci. Eng. 2021, 9, 566. [CrossRef]
  28. Liu, P.; Yao, H.; Dai, H.; Fu, W. The Detection and Following of Human Legs Based on Feature Optimized HDBSCAN for Mobile Robot. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; Volume 2216, p. 012009. [CrossRef]
  29. Asyaky, M.S.; Mandala, R. Improving the Performance of HDBSCAN on Short Text Clustering by Using Word Embedding and UMAP. In Proceedings of the 2021 8th International Conference on Advanced Informatics: Concepts, Theory and Applications (ICAICTA), Bandung, Indonesia, 29–30 September 2021; pp. 1–6. [CrossRef]
  30. Liu, J.; Sun, S.; Chen, C. Big data Analysis of Regional Meteorological Observation Based : On Hierarchical Density Clustering Algorithm HDBSCAN. In Proceedings of the 2021 2nd International Seminar on Artificial Intelligence, Networking and Information Technology (AINIT), Shanghai, China, 15–17 October 2021; pp. 111–116. [CrossRef]
  31. Alexopoulos, E.C. Introduction to multivariate regression analysis. Hippokratia 2010, 14, 23. [PubMed]
  32. Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer ; John Wiley & Sons, Ltd.: West Sussex, UK, 2008

作者：
香港科技大學機械及航空航天工程系助理教授Rhea Liem教授
香港科技大學機械及航空航天工程系博士生Jefry YANTO先生

學術編輯： Xavier Olive

收文日期：2022 年 8 月 25 日
接受日期：2022 年 10 月 17 日
出版日期：2022 年 10 月 20 日

出版人說明：MDPI 對於出版地圖的司法管轄權主張和所屬機構關係保持中立。


版權所有：© 2022。作者保留版權。被許可人瑞士巴塞爾 MDPI。本文章乃根據共享創意特許條款 (CC BY) (https://creativecommons.org/licenses/by/4.0/) 分發的開放取覽文章。

關鍵字：飛機燃料模型；主成分分析；基於分層密度之噪聲應用空間聚類法；多元線性迴歸法

2023年6月