用以对新航线所需燃料作出髙效预算的飞机燃料聚类估算模型


摘要：燃料消耗占飞机的整体营运成本比例达 25%，是航空公司至为重大的决策因素之一。因此，对燃料消耗作出审慎的估算，是航空公司在未来一个财政年度里确保顺利营运的关键工作。当航空公司需要估算新航段的总燃料消耗量，而又未能掌握所需数据时，就会出现困难。这便需要有一个强大的参数模型，即使在缺乏相关数据的情况下，也可以借助该模型所描绘的新航线特征，来作出相关推演工作。为解决这个问题，我们提出一个涉及两个步骤的方法，来得出一个可用以准确地估算所需飞机燃料的模型。这个构建出来的方法既涉及无监督学习，也涉及一个回归模型。对于无监督学习步骤，采用「基于分层密度之噪声应用空间聚类法」(HDBSCAN)，来对经过主成分分析 (PCA) 方法归约出的数据进行聚类处理。这个步骤可以在过滤数据中的噪声后，根据各个航段的主要成分所显示的基本特征，自动分类不同的航段。然后，使用多元线性回归法 (MLR) 推演出每个聚类的公式。主要成分分析基础聚类模型被证明优胜于对单一飞机类型采用一通用的模型。对于每个聚类内的现有航线，使用这种方法得出的燃料估算之均方根误差小于 5%。更重要的是，这个建议使用的方法可用以准确地估算新航线所需的总燃料，总误差小于 2%，因此能够解决航空公司燃料估算研究的其中一个现有局限性。

关键字：飞机燃料模型；主成分分析；基于分层密度之噪声应用空间聚类法；多元线性回归法

1. 简介

航空大数据分析在近年以来已经成为一个新兴的研究领域 [1]。由于数据的收集和储存方面有所进步，数据驱动模型或机器学习技术已广泛地应用于不同的行业，而航空业也不例外 [2]。采用这些技术，能帮助从任何特定的数据集中发现有意义的模式和知识 [3]。先前使用这些技术在航空领域进行的研究之结果，已在航空交通管理 [2]、飞机意外调查 [4]、飞行运作异常 [5]、航空公司飞机性能 [6] 等不同方面得到体现。

由于燃料成本占航空公司总营运开支的 17-25%，航空公司的一个飞机性能关注点就是燃料消耗量 [7]。正因为燃料预算决定了航空公司在未来一年的盈利能力，因此，具有可靠而且准确的燃料估算模型，对于航空公司来说十分重要。燃料预算取决于耗用的燃料数量及预期的燃料价格。我们明白，燃料价格的波动是决定燃料预算的一个关键因素 [8, 9]。但是，燃料价格的预测不在这项研究的范围之中，而且我们假设各家航空公司都有适当的策略和政策来应对燃料价格的波动问题。在这项研究中，我们聚焦于估算在制定燃料预算时考虑的燃料数量，我们在下文将其称为燃料消耗估算。为尽量降低由于燃料计划欠妥造成的损失，有必要实现高度准确的总燃料预测。航空公司花费在燃料上的开支高达数以十亿计美元，因此，即使是 1% 的准确度偏差也会涉及大笔的款项。例如某家本地旗舰航空公司在 2021 年录得总燃料成本 94 亿港元（约 12 亿美元）[10]；这金额的 1% 已是大约 1,200 万美元。经与航空公司伙伴讨论之后，我们了解到，可以假设平均需要的燃料等同于前一年的使用量，从而依靠统计分析，来估算现有航线的总燃料量。对于一些航段接著航段的情况，有可能需要作出轻微的调整，而这种调整通常是根据专家的意见和过往经验决定的。由于假设个别航班的燃料预测的过高估算及过低估算将会在总计层面上互相抵销，因此以上做法通常会忽略每次飞行的燃料消耗差异。图 1 说明这个假设的有效性，当中显示了在不同航段飞行的特定飞机机型的燃料消耗量的逐年变化。x 轴显示飞行航段（即始发地与目的地），而 y 轴则显示标准化的燃料消耗量（请注意，为保密原因，未能显示实际的燃料消耗数值）。值得注意的是，使用不同的飞机机型时，燃料消耗的分布可能会有所不同。虽然趋势看来一致，但由于缺乏数据，在考虑新的航段时，这种统计方法不会奏效，如图 1 右侧所示。


图 1：不同航段的燃料消耗分布（2014 年至 2017 年）

在相关文献里，存在多种燃料消耗的估计模型，当中包括较简单的模型以至复杂得多的模型。不同类型的模型针对不同的目的，包括从一次飞行的详细计算，以至每日到每年营运的较低层次计算。下文载有关于这些模型的概述，以及说明为何它们不适合用来处理正待处理的特定问题。

有些研究聚焦于用尽可能多的细节来表现飞行操作。例如 Lyu 及 Liem [11] 透过就整个飞行任务的轮廓整合出逐个分段的航程公式，开发出一个详细的飞行任务分析程序。为进行更为逼真的计算，根据实际飞行的数据，对任务轮廓进行参数化。Sun 等人 [12] 开发了一种建基于飞行运动公式的飞行模拟，来估算飞机在飞行期间的燃料流量。此外，Kim 等人 [13] 近期开发了一种数据增强型飞行模拟，当中具有引伸自实际操作数据的一些限制，用以密切地模拟实际运作。Lee 及 Chatterji [14] 则基于飞行运动公式，开发了一个较为复杂的飞行模拟模块，可以实现更高的准确度，而且起飞重量误差小于 1%。但是，这些方法都需要掌握到飞行中涉及的复杂和详细的资料。另外，由于各家航空公司每年都有数百甚至数千次的航班，这些方法的计算成本太高，因此不适合用于进行燃料策划的工作。

另一方面，一些研究人员则推演出一些较简单的经验性模型，这些模型的计算成本要低得多，但却会牺牲结果的准确性。这种方法更常用以预测总燃料消耗量，而对于每次飞行的燃料预测之准确性则并不重要。O'Kelly [15] 根据经验，就飞机的大小及飞行距离，推演出一个线性回归结果。Yanto 及 Liem [16] 则通过结合低逼真度的Bréguet航程公式和高逼真度的飞行模拟结果，推演出一个多种逼真度的燃料消耗估算方法。此方法特别有利于预测匀速航段并不是主要部分的短途飞行的燃料消耗。在该方法下，为便利进行简单的总燃料消耗计算，针对每种飞机机型，推演出一个线性回归模型，净载重量及飞行航程都是其输入因素。Kang 及 Hansen [6] 也开发出聚类专属的集成学习法，来估算燃料消耗量。他们执行了一个建基于稳定性的 K 均值算法，来对美国的飞行航班进行聚类处理，而结果显示，飞行航班的燃料表现乃取决于飞行方向。至于为航空公司开发的燃料预测模型，一些研究人员对二氧化碳排放量估算 [17]、燃油装卸量 [18]、载运成本 [6, 19]、爬升及进场航段的燃料预测 [20] 等进行了研究。但是，据我们所知，现时尚没有任何研究是聚焦于航空公司燃料预算目的之燃料预测模型建构的。虽然有一些模型可用以预测总燃料消耗量，但正如上文所指，它们都不是专门为航空公司的燃料预算目的而推演出来的。首先，航空公司未必有用于建构这些模型的完全相同的数据集，也就限制了这些主要基于数据的模型的应用。其次，正如上文所指，航空公司燃料预算的准确性乃取决于对燃料消耗量的估算及对燃料价格的预测，而前者就是本文的重点。由于涉及多重因素及不确定性，例如航空运输需求、航线变更、飞机性能、大气条件、新航段的引入等，预测未来一年的总燃料消耗量并不容易。举例而言，若某一月份里的乘客数量出人意表地增加，将会导致燃料消耗飙升 [21]。虽然以上大多数因素均已经在统计性方法中加以考虑，但正如前文所指，对引入新航段时的总燃料消耗量作出预测，仍然是航空公司面对的一项公开挑战。因此，航空公司需要有稳健而灵活的燃料消耗估算模型，从而确保能够审慎地编制全面考虑到各种经营性变化（包括引入新的航段）的燃料预算。本文的其中一项主要贡献，正是关于如何建构这样的模型能力。

本文介绍一种新的燃料消耗估算方法，该方法也适用于涉及新航段的燃料预测。有关研究采用了我们的航空公司伙伴分享的实际营运数据。本文提出的方法使用一个借助主成分分析法 (PCA) 的谱理论，透过去除冗余资料，来降低可用数据的维度。这个降维方法有助于避免过度拟合，并且能够得出更为稳妥的结果。之后，通过采用无监督聚类算法，对各个主成分作出航班聚类。在确定各个航段的聚类之后，为每个聚类推演出一个线性回归模型。当有新的航段出现时，我们设计一种方法，根据航线的特征，将新航段投入到其中一个聚类。之后，便可以用为所选择的聚类推演出的线性回归函数，来估算该个新聚类的燃料消耗量。对于该方法能否预测新航段的燃料消耗量，将根据其预测准确性和涉及的计算复杂程度，来加以评估。特别是该模型需要满足航空公司的要求 — 在此情况下，我们参考了我们的航空公司伙伴的要求，亦即要做到总误差小于 3%。

本文划分为以下章节。第 2 节描述这次提出的方法，包括当中采用的数据和研究方法。第 3 节介绍该方法得出的结果，并附上其验证证据，同时还探讨将这个方法用于新航段时的表现。第 4 节对这方法和其结果作出总结。

2. 研究方法

我们提出一种系统性的方法，来帮助航空公司估算总燃料消耗量，用于针对现有的和新的航段，制定燃料预算之目的。我们提出的方法包含两个步骤，步骤 1 是采用「基于分层密度之噪声应用空间聚类」(HDBSCAN) 算法的无监督学习，步骤 2 是一线性回归模型。这个双重步骤法如图 2 所示。在步骤 1（以蓝色箭头表示）当中，我们执行 HDBSCAN 算法，根据该算法计算出的密度资料，自动对数据进行分组。图 2 显示的聚类数目（三个）只是作为示意，其中每一种颜色的点表示一个独特的聚类。通过执行 HDBSCAN 算法得出的聚类数目取决于正待处理的具体问题。在我们将数据放入 HDBSCAN 之前，我们使用主成分分析法 (PCA) 减低问题的维度，只保留在认定输出结果的过程中占有主导作用的输入成分。在对数据进行聚类处理后，我们展开步骤 2。在步骤 2（以红色箭头表示）当中，我们为每个聚类推演出一个线性回归函数，以燃料消耗量作为输出项目。


图 2：开发出的用以估算燃料消耗量的双重步骤法。请注意，此处显示的三个聚类只是作为示意（该三个聚类以三种不同颜色表示，颜色乃随意选定）；不同聚类数目的情况均适用这个方法。

在预测特定航段的总燃料消耗量时，我们遵循相同的步骤，首先确定有关航段（不论是现有的还是新的航段）所属的聚类，然后使用相应的线性回归模型来预测燃料消耗量。

2.1. 航空公司所纪录的飞行营运数据

我们采用了我们的航空公司伙伴提供的营运数据来撰写本文。有关数据在飞机于地面时（即起飞前和著陆后）进行记录，储存于飞行后期信息系统 (PFIS) 之中。因此，这些数据不像以 1 Hz 频率进行纪录的快速存取记录器 (QAR) 数据那样详细。表 1 载列了在模型推演过程中考虑的各种输入因素；这些因素是根据我们与航空公司伙伴旗下从事燃料消耗表现评估和估算工作的工程师互相讨论确定的。表现系数特征 (Perf) 乃指飞机燃料表现相对于最佳状态的偏差：若是负值的话，表示表现较差，而正值则表示表现较好。

表 1：我们的研究中使用的 PFIS 记录数据列表



在模型的推演过程中同时使用飞行时间和地面距离资料也许看似多余。但是，这两种资料其实是相辅相成的。地面距离资料决定了基本航程资料，而飞行时间则考虑了速度、爬升率和下降率、高度分配、空中交通拥堵期间的等待和盘旋情况等。换言之，飞行时间隐含了飞行期间各种操作变化的资料，因为尽管不同航班可以有相同的始发地及目的地，但没有飞行路径是完全一样的。关于飞行日期特征，我们只采用月份资料。月份变量 (m) 被转化为一正弦函数，表示为 ，以捕捉季节性影响。在本研究中，我们使用了采用波音 777-300ER 飞机飞行的 11 个进入或离开香港的始发地与目的地组合或航段，以及采用空中巴士 330-300 飞机飞行的 9 个航段的相关数据。所有具代表性的航段都是根据 2014 至 2017 年期间的航班总数，我们的航空公司伙伴就每种机型营运的顶级航段。在选定具代表性的航段时，短途航班（少于 6 小时）和长途航班（多于 6 小时）[22] 都已考虑在内。采用波音 777-300ER 飞机飞行的航段包括飞往或飞离纽约 (JFK)、多伦多 (YYZ)、洛杉矶 (LAX)、三藩市 (SFO)、温哥华 (YVR)、伦敦 (LHR)、巴黎 (CDG)、南非豪登省 (JNB)、悉尼 (SYD)、新加坡 (SIN) 和台北 (TPE) 的航班。采用空中巴士 330-300 飞机飞行的航段包括飞往或者飞离墨尔本 (MEL)、珀斯 (PER)、新加坡 (SIN)、吉隆坡 (KUL)、日本关西 (KIX)、上海 (PVG)、马尼拉 (MNL)、台北 (TPE) 和高雄 (KHH) 的航班。所有这些航段在本文其余部分都称为现有航段。

我们也为每一飞机机型选择了一些「新航段」，来评估我们建构的解决方案在实现预期目标方面的有效性。采用波音 777-300ER 飞行的新航段包括飞往芝加哥 (ORD)、法兰克福 (FRA)、墨尔本 (MEL) 和曼谷 (BKK) 的航班。采用空中巴士 A330-300 飞行的新航段包括飞往悉尼 (SYD)、槟城 (PEN)、仁川 (ICN) 和曼谷 (BKK) 的航班。请注意，这些其实是由我们的航空公司伙伴营运的现有航段，以确保确有数据可供验证。但是，这些数据被严格用来验证所建构方法的有效性，并且在训练过程中被当作「不能看到」。验证过程将在第 3.3 节里加以描述。使用这些「新航段」来验证我们的模型，将会凸显我们的模型在没有过往数据之情况下预测总燃料消耗量的有效性。

2.2. 谱分解

主成分分析 (PCA) 是使用至为广泛的多变量统计性方法，在多个科学领域都有应用 [23]。使用主成分分析法之目的，是从有关数据中提取关键的资料，并只保留最为重要的资料，从而减小数据集的规模。有关的主成分 (PC) 乃由多个正交基函数建构而成，这些函数基本上是相关原始基础的线性组合。使用者可以根据所需的准确度水平和可用的计算预算，来决定代表有关数据集的主成分数目。 当各项数据都处于相似范围内时，主成分分析法的效用会更好，而这可以通过将数据的平均值居中为零，并将各项数据除以标准偏差来实现。首先，我们对含有 n 个样本和 m 个特征的数据 X 进行奇异值分解 (SVD) 分析，将其分解为一个所需的新维度 Nd ，如下面所示：

X = LDRT,

(1)

当中 L∈Rn × Nd包含左奇异向量，R∈R Nd×m包含右奇异向量，而D是由奇异值构成的对角矩阵。请注意，D2是由XTX及XX T的（非零）特征值构成的对角矩阵。之后，我们就可以找到主成分 (P) 的投影如下：

P = LD = XR.

(2)

关于主成分分析的详细解释，可见 [23]。

2.3. 聚类算法

Campello 等人 [24] 提出 HDBSCAN 作为基于密度的噪声应用空间聚类的扩展。这两种方法都是使用基于密度的聚类技术得出的。HDBSCAN 透过引入分层聚类方法，可提高聚类结果的表现。在 HDBSCAN 里，我们无须先行界定聚类的数目，因为该算法会根据密度，自动为每个聚类界定阈值。关于 HDBSCAN 的详细解释，可见 [25]。Python 语言编程使用者也可经 https://hdbscan.readthedocs.io/ 访问所需的程序库（于 2022 年 10 月 16 日进行访问）。HDBSCAN 已经成功地应用于轨迹聚类 [26, 27]、运动识别 [28]、文本识别 [29]、气象预测 [30] 等一些现实问题上。

2.4. 回归分析

多变量线性回归模型是一个用以表示输入变量X∈Rn×m及输出变量Y ∈ ℝn之间关系的一个线性公式 [31]。让我们将Y及X表示为：


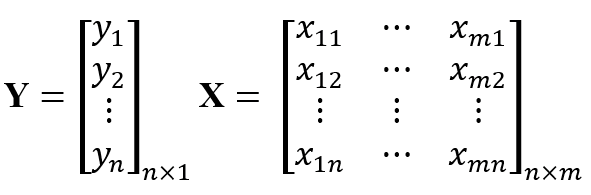
当中n及 m已先行界定；通常 n > m。之后，该个多变量线性回归模型可以表示为：

Y = B + XC + ∆,

(4)

当中B ∈ ℝn 含有有关的偏置项，C ∈ ℝm含有该线性公式的系数，而∆ ∈ ℝn 与残差项目相对应。只需要求解出将 ∆最小化的最小平方，就可以求解出 B及C。这个函数将会用于本文里的回归模型。

3. 结果及讨论

在本节里，我们会介绍这个构建出的参数化燃料消耗量模型的结果，并将其与现有的一些方法进行比较。为进行比较，我们根据我们之前的工作成果，为每一飞机机型推演出一项线性回归 [16]。我们在下文将此模型称为通用模型。我们把可用数据分为一个训练集及一个测试集。我们随机地从每一航段抽出 2014 至 2016 年的 800 个航班样本作为训练集，而测试集则包括 2017 年的航班。样本的数目乃根据每一航段可供采用的最少航班数目而决定。 这个采样方法有助确保数据在所有航段之间分布得更加平均，以避免特定航段出现过度拟合的情况。图 3 显示就第 2.1 节所列出的现有航段和新航段的测试集得出的通用模型预测表现。x 轴显示按最长至最短飞行时间排列的航段（包括出境和入境航班），而 y 轴则显示以公斤为单位的均方根误差 (RMSE)。通用模型显示波音 777-300ER 的 RMSE 最高为 3,300 公斤，而空中巴士 330-300 的 RMSE 则最高为 2,000 公斤。在新的航段里也观察到类似的误差范围。


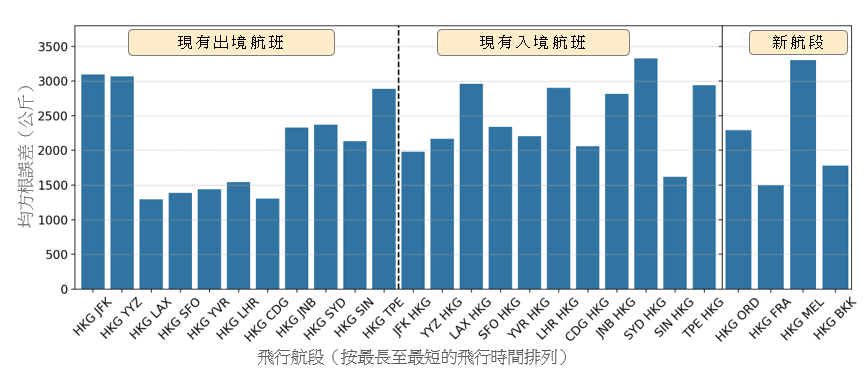
(a) 波音 777-300ER


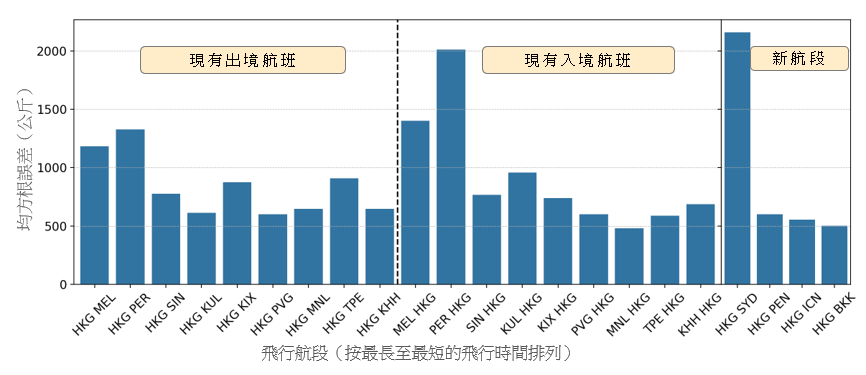
(b) 空中巴士 330-300

图 3：通用模型在测试集得出的预测表现，按现有的出境、入境航班以及新航段分别列出。有关航段乃按最长至最短的飞行时间排列。

根据图 3 所显示，这项研究中考虑的两种飞机机型都没有观察到有甚么趋势。这表明每个航段都有独特的燃料消耗表现。因此，有可能需要采用一个针对逐个航段模型，为每一航段推演出一个线性回归，以捕捉每一航段的独特性。可是由于缺乏航段的数据和适当的回归模型，这种针对逐一航段的模型不能用来预测新的航段的总燃料消耗量。当这个情况出现时，我们可以选择另一「相似」的航段作为参照并借用其回归函数，但是，这种做法过于主观。在本文中，我们致力设计一种更系统化的方法，来为新的航段获取合适的回归函数，以消除上述的主观性。这个称为主成分分析基础聚类模型，以及这个我们构建的模型的表现，会在第 3.1 节里加以解释。为了进行更全面的比较和模型评估，我们亦利用相同的数据集推断和演示另一个建基于聚类的线性回归模型，即简单聚类模型。

这个简单聚类过程完全以国际航空运输协会 (IATA) 建议的距离 / 飞行时间为基础 [22]。换言之，这个简单聚类过程并非遵循任何系统性的方法。表 2 是对这项研究中考虑到的四个回归模型的总结。

表 2：用以预测燃料消耗的不同回归模型以及各自应用于新航段上的情况之总结



从敏感性分析角度了解我们构建的模型，所得出的更深入详情，将在第 3.2 节作出介绍。要记得，本文提出的方法的其中一个关键功能和贡献，是在没有数据的情况下对新航段的总燃料消耗量作出预测。我们将在第 3.3 节里演示以上功能。

3.1. 主成分分析基础聚类模型

我们所构建出的主成分分析基础聚类模型，代表著一种更为系统性、更加稳妥的方法，由于它能够系统性地识别和量化飞行航段的基本特征，并能够将这些资料用于模型的推演过程之中，因此这个方法适合用于预测新航段的总燃料消耗量。在本节里，我们就两种飞机机型展示我们的方法（如第 2 节所解释）。波音 777-300ER 飞行航班的聚类结果（步骤 1）见于图 4a。我们使用「统一流形逼近及投影」(UMAP) 技术来说明二维空间中的数据（https://umap-learn.readthedocs.io/（在 2022 年10 月16日取览））。当中的两个轴表示执行投影算法时，数据点在流形中的位置。x 轴是第一个流形轴，y 轴是第二个流形轴。由于在我们的分析中未有使用流形投影的确切值，为简单起见，未在标绘图中显示各个代码。左图显示原始数据，每种颜色代表著一个不同的航段。那些数据是分散的，为每个航段构建了一些小聚类。换言之，该标绘图并未揭示相似的特征在不同聚类之间存在著什么模式。一经我们对那些数据执行主成分分析，就会出现三个截然不同的聚类，就如中间那个图所显示那样（各个数据点仍然按照其所属航段编以适当颜色）。HDBSCAN 亦自动将这些聚类标示为三个不同的聚类，正如右图的不同颜色所显示。可以看到，主成分分析 (PCA) 和 HDBSCAN 将长途航段分成两批。我们将这两个长途聚类分为飞往澳洲的长途洲际航班（橙色）（下文称为 LH-AU B773ER）和飞往美国及欧洲的长途洲际航班（绿色）（下文称为 LH-US-EU B773ER）。短途航段则归为一组并名为短途（蓝色），下文称为 SH B773ER。为更好地说明这个聚类方法的结果，这些以颜色显示的航班在图 4b 的世界地图上显示；新的航段（红色）亦有在图中显示，以便说明。简单聚类法只会将航班分类为短途和长途航班，而采用我们提出的方法得出的聚类与使用简单聚类法得出的聚类并不相同。


(a)


(b)

图 4：对波音 777-300ER 飞机实施建议中方法的视觉化表示。(a) 左图显示在实施主成分分析 (PCA) 之前的数据。中图显示经过 PCA 程序之后聚类成三组的数据。右图显示 HDBSCAN 聚类的结果。(b) 在世界地图上显示的航段聚类，包括新的航段。

图 5a 显示对于空中巴士 330-300 飞行航班的类似聚类结果。有关航段现在分为两个聚类，就是飞往澳洲的长途洲际航班（粉红色）(LH-AU A333) 以及短途航班（橄榄色）(SH A333)。与前文一样，图 5b 在世界地图上显示各个预计飞行航段及其聚类标识。

以上提出的两个结果显示，飞往澳洲的洲际航班具备独有的特点，因为不论采用哪种飞机机型，这些航班都自动与其他航班分开。这表明除了飞行航程外，始发地或目的地的地理位置也会影响到飞行特性以及燃料消耗表现。要记得，澳洲具有与北半球国家相反的季节性特征。第 3.3 节所介绍的主成分分析基础聚类结果与简单聚类结果之间的比较，将会揭示有必要找出与距离相关的特征之外的飞行特征。


(a)


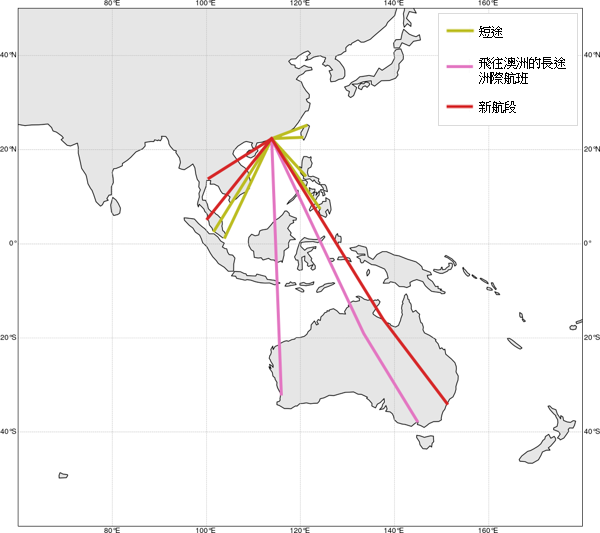
(b)

图 5： 对空中巴士 A330-300 飞机实施建议中方法的视觉化表示。(a) 左图显示在实施主成分分析 (PCA) 之前的数据。中图显示经过 PCA 程序之后聚类成三组的数据。右图显示 HDBSCAN 聚类的结果。(b) 在世界地图上显示的航段聚类，包括新的航段。

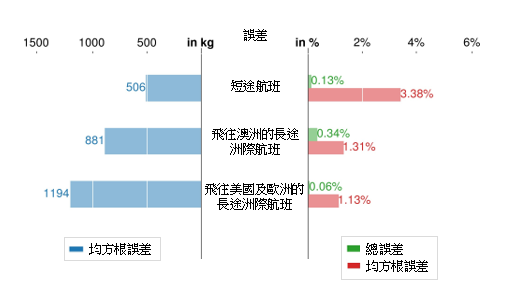
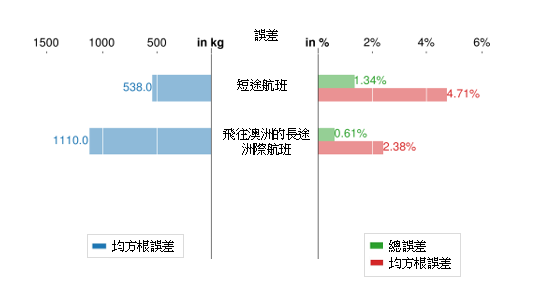
在步骤 2里，我们要为每个采用 HDBSCAN 定义的聚类推演出其线性回归，这些模型在下文中称为主成分分析基础聚类模型。我们之前备用的测试集现在用来验证这些模型；其结果在图 6 中显示。该图以均方根误差 (RMSE)（以公斤及百分率表示）和总误差（以百分率表示）的形式，来显示当中的误差。所有的 RMSE 值都低于 1,500 公斤及 5%。在以公斤和百分率表示的 RMSE 值当中，都观察到不同的趋势。短途航班的以公斤表示的 RMSE 值较小，但以百分率表示的 RMSE 值则比较大。后者是因为据以计算该百分率的燃料消耗参照基准量较低；由于短途航班消耗较少燃料，因此虽然标称误差较低，但百分率仍是较高。所有总误差均低于 1.5%，符合第 1 节所指的航空公司的要求（即低于 3%）。


(a) 波音 777-300ER

(b) 空中巴士 330-300

图 6：对主成分分析基础聚类模型进行验证的结果。左图显示以公斤计算的误差 (RMSE)，右图则显示以百分率计算的误差（总误差及 RMSE）。

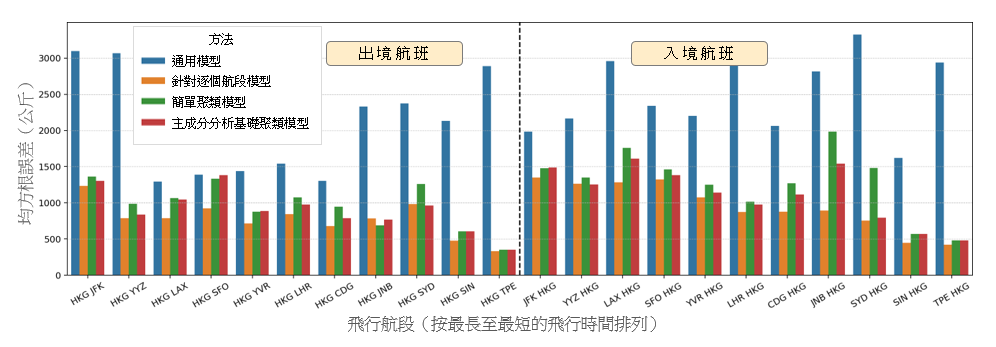
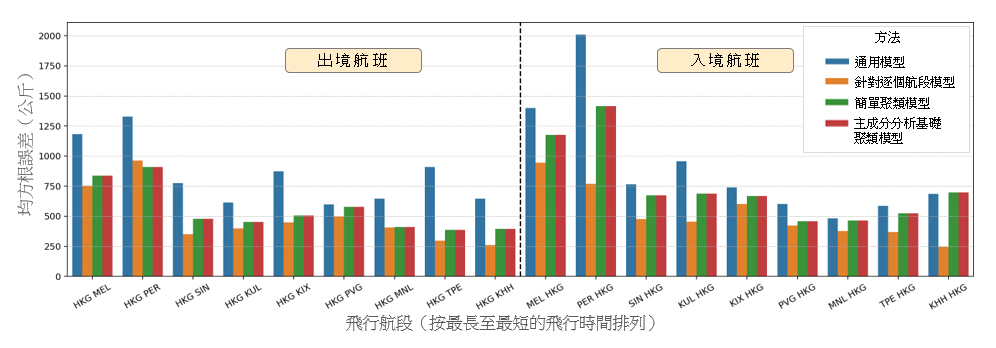
为评估及比较这个新的主成分分析基础聚类模型与表 2 列出的其他模型（即通用模型、针对逐个航段模型和简单聚类模型）的表现，我们使用同一个训练集来训练所有模型，并计算该个测试集的 RMSE。图 7 显示以上四种方法用于该测试集时的表现，x 轴所示的是每个航段（按飞行时间由最长至最短排列），y 轴则显示相应的 RMSE（以公斤计）。结果证明，对于两种飞机机型来说，这个新的主成分分析基础聚类模型的表现都优于通用模型。主成分分析基础聚类模型在波音 777-300ER 的长途航班上的表现也稍佳于简单聚类模型。此外，我们的主成分分析基础聚类模型还有一个额外好处，就是可以用来系统性地预测新航段的总燃料消耗量。第 3.3 节将就此作出演示。这些结果凸显出，为每一个飞机机型推演一个通用的燃料消耗估算模型的方法，并不足以代表（基于飞行航程和地理位置的）不同的飞行特征。此外，若为每个航段推演不同的模型的话，则属于矫枉过正，因为事情会变得更为复杂，却不会显著提高估算的准确性。聚类基础回归模型是使用通用模型和针对逐个航段模型这两者之间的一种折衷做法。与简单聚类模型相比，使用我们这个主成分分析基础聚类模型的优点 — 特别是在用于预测新航段的总燃料消耗量方面的优点 — 将于第 3.3 节里详述。


(a)


(b)

图 7：在 (a) 波音 777-300ER 及 (b) 空中巴士 330-300 飞机机型上，四种不同的线性回归模型用于每个航段的测试集上的表现

我们还进行了敏感性分析，找出每个聚类之中的主导性输入因素。有关结果显示了每一聚类的独特性，并将在第 3.2 节有所介绍。该项敏感性分析研究的结果，为预测燃料消耗量时需要的重要特征提出重要的见解。

3.2. 敏感性分析

一般而言，敏感性分析是用来研究每项输入特征对于输出所起的作用 [32]。对于参数性回归模型来说，回归系数提供了可代表该模型的敏感性的资料。在图 8 之中，y轴上的是线性回归系数，x轴上的是聚类标识符；就每一个输入因素标绘出一幅图。在每幅图中，各条灰色长条表示正待研究的输入因素的回归系数（例如左上图里的飞行时间），而主成分分析基础聚类模型的系数乃以图 4 和图 5 当中用来识别各聚类的相同颜色作为识别。

除了 MACLAW 和月份特征外，每个聚类里的针对逐个航段的系数都很相似。这显示这些特征与其他特征相比，较不具备代表燃料消耗量的能力。聚类的各个系数证明与各航段的系数的平均值具有相似的大小和方向。但是，我们注意到，（当比较航段的系数和聚类的系数时）某些特征有不同的大小和方向。要注意，在这情况下，更高的系数不一定意味著对于输出有更显著的作用，因为结果仍取决于该特征的单位和数值。例如，在y = ax 里，若a = 1000 而x 是以克计算的话，计出的结果并不比 a = 1 而 x 是以公斤计算时大，因为得出的结果并无不同。因此，有需要作进一步分析，以了解每个特征对燃料消耗量所起的作用。

为研究聚类模型里每一特征对燃料消耗量所起的作用，我们计算有关的作用平均值，以一百分比率作为该平均值的单位：


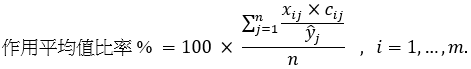
该作用平均值量化了一个回归项目xij×cij（与一特定特征相对应）所需的燃料占有关航程所需燃料总量的平均比例。该作用平均值与聚类模型系数一起在表 3 里显示。粗体数字表示相关特征对于燃料消耗量的作用程度大于 50%，表示该输入特征具有重要性。作用程度小于 10% 的特征则被认为较不重要。


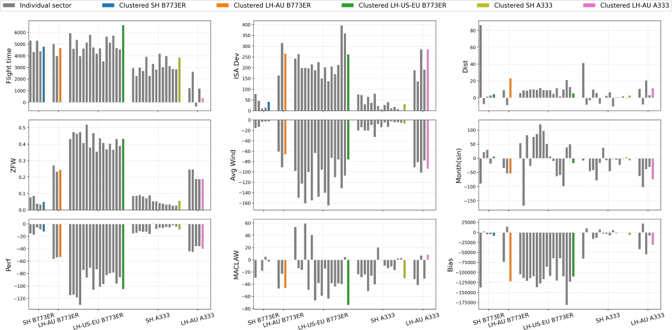
图 8：在不同的聚类下，两种不同飞机机型（波音 777-300ER 及空中巴士 330-300）的线性回归系数之比较

表 3：为波音 777-300ER 及空中巴士 330-300 推演出的聚类基础线性回归模型之系数。对于燃料总量的作用平均值亦以百分比率形式显示。

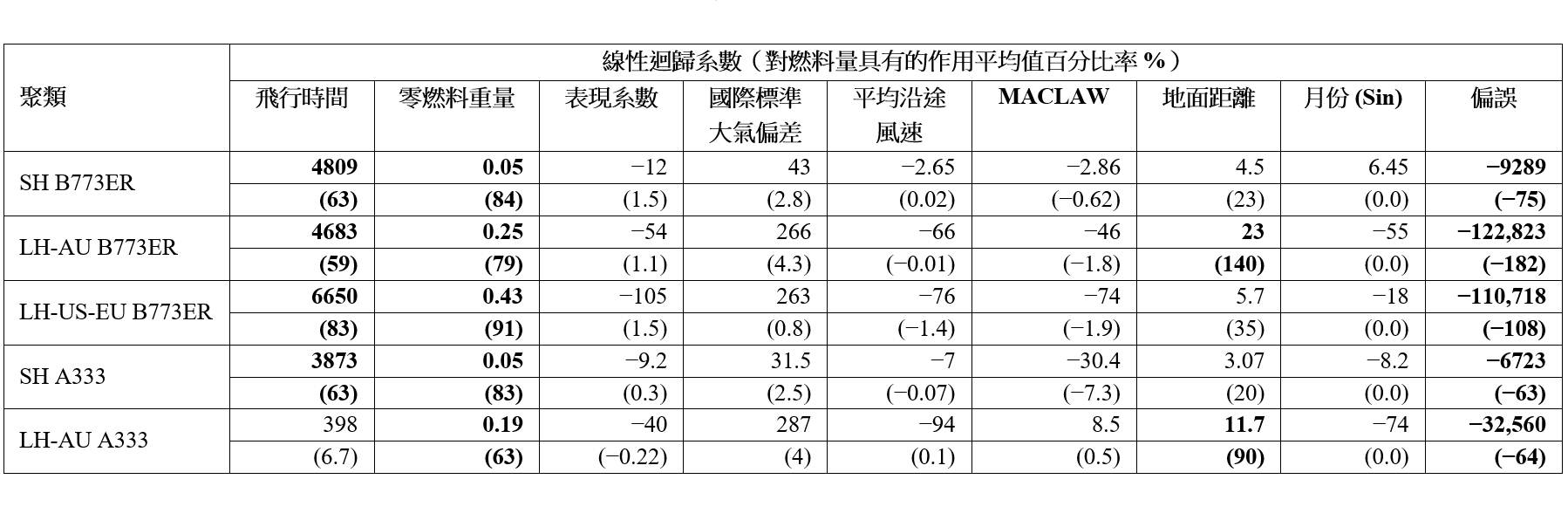
如下文所述，各个具主导性的输入特征可以揭示关于各种飞行航段特征的深刻理解。我们注意到，波音 777-300ER 的燃料消耗主要取决于飞行时间，其次是距离，但长途澳洲航班除外。这项观察结果也与采用空中巴士 330-300 飞行的长途澳洲航班一致，这表示飞往澳洲的航班往往具有相对更为类似的速度轮廓和一致的飞行路线，而飞行时间有较低主导性的影响正是反映此点。另一项有趣的发现是，不论采用以上哪一个飞机机型飞行的短途航班，零燃料重量都较为可观。要注意，零燃料重量与决定燃料消耗量的起飞重量有高度的相关性。由于短途航班的巡航范围较短，但爬升阶段占比更高，以上高度相关性不无道理。爬升过程所消耗的燃料高度取决于飞机的重量，并且对短途航班情况下的总燃料消耗量有可观的影响作用 [11]。有关结果与我们直觉地认为飞行时间、零燃料重量和距离是最重要的特征这点脗合。各个重要特征在不同的聚类之间有不同的系数，这点进一步凸显出对所有航段使用同一组模型系数的通用模型实在不足以用来代表不同的飞行航段特征。

3.3. 对于新航段的预测

新航段的定义是没有任何历史数据的始发地与目的地组合。为了进行航线规划和初步分析工作，大部分的航空公司都使用一飞行规划系统 (FPS)，来取得合理的飞机资料（例如飞机和性能因素）、航线资料（例如飞行时间和距离）以及气象资料（例如风速等）。但是，所得出的预测并不很准确，因为大部分的操作性变化都没有被顾及到。故此，航空公司不能单单倚赖 FPS 的预测来估算新航段的燃料消耗。

在这次研究里，除了用以训练有关模型的航段外，我们还借用一些现有航段来模拟新的航段，详如第 2 节所述。通过此举，我们可以根据可用的燃料消耗资料适当地验证有关模型。验证有关模型的方法，是依循均方根偏差 (RMSE) 和总误差在第 3.1 节中的定义和用法，评估均方根偏差 (RMSE) 和总误差。此外，我们也将采用主成分分析基础聚类模型获得的结果，与采用通用模型和简单聚类模型得出的结果进行了比较。

以我们的主成分分析基础聚类模型预测燃料消耗量时，第一个步骤是为有关的新航段界定适当的聚类。在妥善地界定每个聚类内的航段特征之后（例如飞往南半球的长途航班、飞往北半球的长途航班、短途航班等），便能够合理地以人工方式编配有关聚类。例如，由于香港至墨尔本 (HKG-MEL) 与香港至悉尼 (HKG-SYD) 相似，因此可以归类为长途澳洲聚类。一经界定聚类，我们就可以简单地使用以飞行规划系统 (FPS) 生成的新航段的相关输入，来运用相应的回归模型。图 9 显示对前述两种飞机机型运用三种不同的模型（即通用模型、简单聚类模型和主成分分析基础聚类模型）之结果比较。结果显示，与通用模型相比，使用聚类模型具有明显的优势。这就表示通用模型并不足以代表飞机营运中涉及的航段变化。在此项研究中，与空中巴士 330-300 相比（空中巴士只有长途和短途聚类），波音 777-300ER 的航班具有更为多样化的航段（基于主成分分析 (PCA)，波音 777-300ER 的航班得出三个聚类）。要记得，简单聚类模型只是根据飞行航程（短途或长途）来决定，而并不区分始发地 / 目的地的地理方向。因此，主成分分析基础模型和简单聚类模型就空中巴士 330-300 的航班得出相同的预测结果和有相同的准确性也就不足为奇。对「新的」香港至墨尔本 (HKG-MEL) 航段采用主成分分析基础聚类模型预测其燃料消耗量时，可以清楚地观察到误差指标有所减少，这个主成分分析基础聚类模型的优越性可见一斑。上述误差指标的减少，是因为主成分分析基础聚类程序可以自动识别出不同的长途航班（美国和欧洲至澳洲）之间的不同特征。在这项研究中，由于数据所限，在证明我们构建的方法的优点时存在限制。当在训练过程和聚类过程之中考虑更多的航段（而且各航段有更多的特征差别）时，采用系统性和自动的主成分分析基础聚类方法的好处将会更为明显。

人们或会怀疑，当可以获得的数据（可变因素的数目）并不如航空公司可以提供的那么多时，我们提出的方法是否适用。生成的飞行规划系统 (FPS) 输入项目往往属于机密，并仅给予航空公司使用。因此，我们还推演出只由三个输入项目（即飞行时间、零燃料重量和飞行距构成的简化版模型。在敏感性分析里，这三个输入项目是最主要的特征，如表 3 所示。要记得，飞行时间和飞行距离特征是互补的；由于飞行轨迹具有三维性质，飞行时间和飞行距离这两者之间的关系不能简单地用速率来描述。由于飞机的速度、高度、空中交通拥挤和中断情况各有不同，两个航班可以飞行相同的距离，但所需的飞行时间却会有分别。为进行比较，我们将具有较少特征的模型称为简化版通用模型和简化版主成分分 析基础聚类模型。这些简化版模型采用表 3 中列出的相同回归系数，但只考虑偏误项目和从航班资料获得的三个输入项目，而其余的输入项目则设置为表 4 所列出的标称值。

请注意，对波音 777-300ER 和空中巴士 330-300 这两种机型均采用这些标称值。这是为模拟可以采用参数性模型、但使用者无法取得详细的航班资料输入项目的情况。之后，我们采用简化版通用模型和主成分分析基础聚类模型的表现，来分析原有的通用模型和主成分分析基础聚类模型；得出结果如图 10 所示。


(a)

(b)

图 9：在 (a) 波音 777-300ER 及 (b) 空中巴士 330-300 飞机机型上，分别采用通用模型、简单聚类模型及主成分分析基础聚类模型来预测新航段的燃料消耗的模型表现比较。上图显示按公斤计的均方根误差 (RMSE) 值；中图显示按百分率计的均方根误差 (RMSE) 值；下图则显示按百分率计的总误差。


(a)

(b)

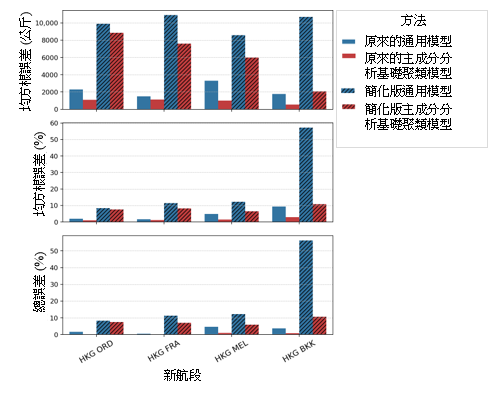
图 10：在 (a) 波音 777-300ER 及 (b)空中巴士 330-300 飞机机型上，分别采用原来的通用模型、原来的主成分分析基础聚类模型、简化版通用模型、简化版主成分分析基础聚类模型来预测新航段的燃料消耗的模型表现比较。上图显示按公斤计的均方根误差 (RMSE) 值；中图显示按百分率计的均方根误差 (RMSE) 值；下图则显示按百分率计的总误差。

表 4：对波音 777-300ER 和空中巴士 330-300 采用简化版通用模型和简化版主成分分析基础聚类模型时，被「排除在外」的输入因素的标称值

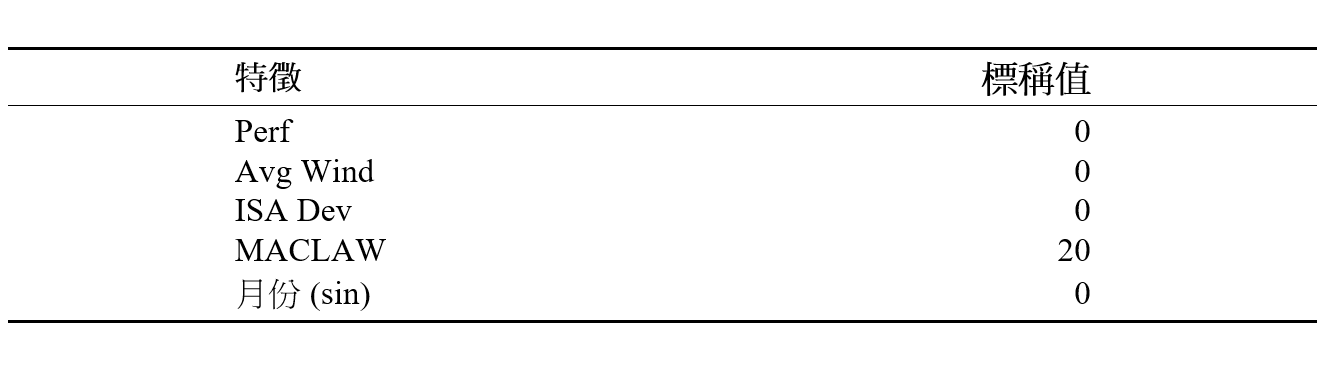
结果显示，简化版的主成分分析基础聚类模型仍具有可以接受的准确度。虽然所有简化版通用模型都显示出比相应的简化版主成分分析基础模型有较高的误差，但图 10a 显示，当这两种模型运用于香港至曼谷 (HKG-BKK) 航段时，两者之间的准确性差异明显更大。进一步调查发觉，实际平均表现因数 (-16%) 与假定标称值（如表 4 所示的 0%）之间的偏差是导致有上述更大误差的部分原因。通用模型的 Perf 系数是 -84，但主成分分析基础聚类模型的 Perf 系数却是 -12（如表 3 所示）。故此，通用模型和简化版通用模型之间的预测差异 (-84 × Perf ) 比主成分分析基础聚类模型和其简化版之间的预测差异 (-12 × Perf ) 更为巨大。图 11 说明了为简化版模型选择适当的标称值的重要性。当中显示，当标称的 Perf 值更为接近实际平均值时，均方根误差 (RMSE) 便会降低。请注意，由于其他航段的平均 Perf 值（范围在 -5% 和 5% 之间）较接近假定的标称值，其他航段并没有观察到大幅度的差异。


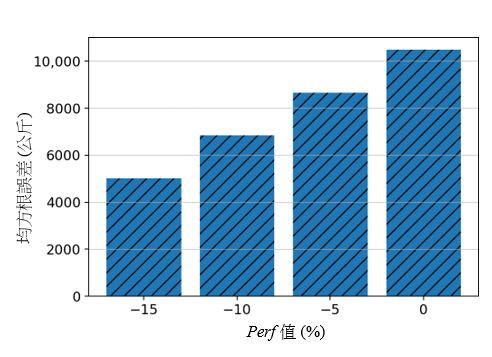
图 11：在不同 Perf 标称值情况下，对香港至曼谷 (HKG-BKK) 航段运用简化版通用模型时的均方根误差 (RMSE) 值。这显示当标称 Perf 值更为接近实际平均值 (-16) 时，准确度将会提高。

以上结果显示，即使欠缺某些真实的特征值，但我们建构的主成分分析基础聚类模型很一致地具有优于通用模型的表现。此外，这个简化版的主成分分析基础聚类模型更容易地为其他使用者所采用，因为只需要有基本的航班资料作为输入项目即可。

4. 结论

我们展示了一种用以估算燃料消耗量的新方法。由于我们采用的资料和数据乃航空公司可以具体取得的数据，因此该方法对于航空公司的预算编制应很有用。我们的其中一个主要目标是构建一种方法，来系统地预测除现有航段外的新航段总燃料消耗量，从而设法解决现有模型的局限性。我们具体上构建了一个主成分分析基础聚类模型，并对波音 777-300ER 及空中巴士 330-300 这两种飞机机型运用了这个构建的方法。结果显示，由于不同的飞机机型有不同的燃料表现特性，故此有必要为每种飞机机型推演出专属的燃料模型；这些结果符合我们之前的观察 [16]。

此外，我们的研究显示，对每种飞机机型采用一个通用的线性回归模型（这种做法在其他燃料模型中普遍采用）是不足够的。这是由于在不同航段里的燃料表现并不相同。换言之，燃料消耗量不单单取决于飞机航程，还取决于任务概况和航班涉及的地点。由于不同类型航班有不同的主要阶段，故此短途和长途航班具有不同的燃料消耗特性。在短途航班的燃料消耗量当中，爬升阶段占主要部分。相反，在长途航班的燃料消耗量当中，巡航阶段占主要部分 [11]。因此，在推演模型时需要考虑到这项差异，而我们在推演主成分分析基础聚类模型时己经考虑到这点。此外，若使用聚类基础回归模型，便无需推演逐一航段的燃料消耗模型，省却当中涉及的麻烦。

我们并不采用以人手方式将各个航段划为短途或者长途航班，而是使用 HDBSCAN 作为无监督聚类方法，建构出一个主成分分析基础聚类方法。使用主成分分析法，有助揭示原本在单单考虑原始的输入因素时不同航段里一些并不明显的特征。以波音777-300ER 飞行的航段被聚类为三个组别，分别是短途航班、长途澳洲航班以及长途美国及欧洲航班。与此同时，以空中巴士 330-300 飞行的航段则聚类为两个组别，分别是短途航班和长途澳洲航班。通过对每一聚类作出清晰的特征描述，便可以在缺乏数据的情况下，轻易地将新的航段投入到其中一个聚类。在这项研究中，由于我们的航空公司伙伴分享的数据较为有限，因此我们只考虑了少数几个航段。当涉及更多航段时，聚类程序有可能会更加复杂，并且如果有关的聚类基础线性回归的准确度不能符合要求，则可能需要进行分层的聚类。

我们已展示了采用主成分分析基础聚类模型来估算现有航段和新航段的燃料消耗量之好处。这个模型在计算效率、有效性和直观性之间作出平衡取舍。由于这个模型具有参数化的性质，其他人即使无法取得用于构建模型的原始数据集，也无碍使用该模型，因此这个模型具备更为广泛的适用性。这次建构的主成分分析基础聚类模型的准确性，乃通过评估均方根误差 (RMSE) 和总误差来加以验证。结果所有的 RMSE 值均低于 5%，所有的总误差均低于 2%，当中均已包括新航段的燃料消耗量预测。这样的预测能力符合我们的航空公司伙伴的要求，亦即总误差要小于 3%。我们还证明了简化版主成分分析基础聚类模型（只考虑了三个关键的输入项目而对其他因素发配标称值）尽管未有包含一些资料，但仍然提供充分的准确性。当使用者无法取得除飞行时间、零燃料重量和飞行距离以外的飞行资料时，这不失为一个实用、有助益的方法。

我们这个新的燃料估算方法结果令人鼓舞。由于我们这个解决方案具有以数据为基础的性质，同一方法可以在对应不同飞机机型、燃料种类、航段、航空公司等的不同数据集上运用。得出的模型可用以进行比较，从而进一步丰富我们的燃料消耗量估算研究，以及有助更深入了解飞机燃料表现。

各作者负责部分： 概念化：J.Y. 及 R.P.L.；数据治理：J.Y.；方法学：J.Y.；验证：J.Y.；撰写 — 准备初稿：J.Y.；撰写 — 审阅及编辑：R.P.L.；监督：R.P.L.。所有作者均已阅读并同意采用此手稿的出版版本。

资金：此项研究并无得到外界资助。

数据可用性声明：不适用

鸣谢：此项研究中使用的数据，乃由国泰航空公司根据该公司与香港科技大学机械及航空航天工程学系订立的数据合作协议提供，作者谨此向国泰航空公司致以衷心谢意！作者亦由衷感谢 Steve Yip 先生在此项研究中参与讨论并提供寳贵建议。

利益冲突：作者声明并无利益冲突情况。

缩略语：
本文使用以下缩略语：

HDBSCAN 基于分层密度之噪声应用空间聚类法
PCA 主成分分析
PFIS 飞行后期信息系统
QAR 快速存取记录器
RMSE 均方根误差
UMAP 统一流形逼近及投影技术

参考资料：


  1. Akerkar, R. Analytics on Big Aviation Data: Turning Data into Insights. Int. J. Comput. Sci. Appl. 2014, 11, 116–127.
  2. Li, M.Z.; Ryerson, M.S. Reviewing the DATAS of aviation research data: Diversity, availability, tractability, applicability, and sources. J. Air Transp. Manag. 2019, 75, 111–130. [CrossRef]
  3. Burmester, G.; Ma, H.; Steinmetz, D.; Hartmannn, S. Big Data and Data Analytics in Aviation. In Advances in Aeronautical Informatics; Durak, U., Becker, J., Hartmann, S., Voros, N., Eds.; Springer: Cham, Switzerland, 2018. [CrossRef]
  4. Christopher, A.B.A.; Vivekanandam, V.S.; Anderson, A.B.A.; Markkandeyan, S.; Sivakumar, V. Large-scale data analysis on aviation accident database using different data mining techniques. Aeronaut. J. 2016, 120, 1849–1866. [CrossRef]
  5. Li, L.; Das, S.; Hansman, R.J.; Palacios, R.; Srivastava, A.N. Analysis of flight data using clustering techniques for detecting abnormal operations. J. Aerosp. Inf. Syst. 2015, 12, 587–298. [CrossRef]
  6. Kang, L.; Hansen, M. Improving airline fuel efficiency via fuel burn prediction and uncertainty estimation. Transp. Research Part C 2018, 97, 128–146. [CrossRef]
  7. EUROCONTROL. Fuel Tankering in European Skies: Economic Benefits and Environmental Impact. Aviation Intelligence Unit—Think Paper, June 2019. Available online: https://www.eurocontrol.int/publication/fuel-tankering-european-skies-economic-benefits-and-environmental-impact/ (accessed on 16 October 2022).
  8. Kang, W.; Perez de Gracia, F.; Ratti, R.A. Economic uncertainty, oil prices, hedging and U.S. stock returns of the airline industry. N. Am. J. Econ. Financ. 2021, 57, 101388. [CrossRef]
  9. Horobet, A.; Zlatea, M.L.E.; Belascu, L.; Dumitrescu, D.G. Oil price volatility and airlines' stock returns: evidence from the global aviation industry. J. Bus. Econ. Manag. 2022, 23, 284–304. [CrossRef]
  10. Cathay Pacific Airways Limited. Annual Report 2021; Cathay Pacific Airways Limited: Hong Kong, China, 2021.
  11. Lyu, Y.; Liem, R.P. Flight performance analysis with data-driven mission parameterization: Mapping flight operational data to aircraft performance analysis. Transp. Eng. 2020, 2, 100035. [CrossRef]
  12. Sun, J.; Hoekstra, J.M.; Ellerbroek, J. OpenAP: An Open-Source Aircraft Performance Model for Air Transportation Studies and Simulations. Aerospace 2020, 7, 104 . [CrossRef]
  13. 13. Kim, D.; Seth, A.; Liem, R.P. Data-enhanced dynamic flight simulations for flight performance analysis. Aerosp. Sci. Technol. 2022, 121, 107357. [CrossRef]
  14. Lee, H.T.; Chatterji, G.B. Closed-form takeoff weight estimation model for air transportation simulation. In Proceedings of the 10th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Fort Worth, TX, USA, 13–15 September 2010.
  15. 15. O'Kelly, M.E. Fuel burn and environmental implications of airline hub networks. Transp. Res. Part D 2012, 17, 555–567. [CrossRef]
  16. 16. Yanto, J.; Liem, R.P. Aircraft fuel burn performance study: A data-enhanced modeling approach. Transp. Res. Part D Transp. Environ. 2018, 65, 574–595. [CrossRef]
  17. Seymour, K.; Held, M.; Georges, G.; Boulouchos, K. Fuel Estimation in Air Transportation: Modeling global fuel consumption for commercial aviation. Transp. Res. Part D Transp. Environ. 2020, 88, 102528. [CrossRef]
  18. I˙lker Guven Yilmaz.; Kartal, E.; Özen, Z.; Gulsecen, S. Prediction of Fuel Tankering in AviationIndustry with Machine Learning Algorithms. J. Aeronaut. Space Technol. 2021, 14, 19–34.
  19. Ryerson, M.S.; Hansen, M.; Hao, L.; Seelhorst, M. Landing on empty: Estimating the benefits from reducing fuel uplift in US Civil Aviation. Environ. Res. Lett. 2015, 10, 094002. [CrossRef]
  20. Chati, Y.S.; Balakrishnan, H. Data-Driven Modeling of Aircraft Engine Fuel Burn in Climb Out and Approach. Transp. Res. Rec. 2018, 2672, 29, 1–11. [CrossRef]
  21. Litingtung, S.; Consultants, S.M. White Paper: The Fuel Budgeting Complexities. Available online: https://www.aircraftit.com/articles/white-paper-the-fuel-budgeting-complexities/ (accessed on 3 October 2022).
  22. IATA. Air Transport and Travel Industry IATA Edifact and Xml Codeset Version 20.2. Available online: https://cdn.document360.io/4b1f93b7-f7b8-4ebb-81be-c17af837a94f/Images/Documentation/Code%20set%20Directory%2020.2.pdf (accessed on 16 October 2022).
  23. Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [CrossRef]
  24. Campello, R.J.G.B.; Moulavi, D.; Sander, J. Density-Based Clustering Based on Hierarchical Density Estimates. In Proceedings of the 17th Pacific-Asia Conference, PAKDD 2013, Gold Coast, Australia, 14–17 April 2013; Pei, J., Tseng, V.S., Cao, L., Motoda, H., Xu, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 160–172.
  25. McInnes, L.; Healy, J. Accelerated Hierarchical Density Based Clustering. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 33–42. [CrossRef]
  26. Maulydiana, S.F. Probabilistic Approach in Flight Trajectory Modeling for Fast and Efficient Noise Contour Generation. Master's Thesis, The Hong Kong University of Science and Technology, Hong Kong, China, 2019. [CrossRef]
  27. Wang, L.; Chen, P.; Chen, L.; Mou, J. Ship AIS Trajectory Clustering: An HDBSCAN-Based Approach. J. Mar. Sci. Eng. 2021, 9, 566. [CrossRef]
  28. Liu, P.; Yao, H.; Dai, H.; Fu, W. The Detection and Following of Human Legs Based on Feature Optimized HDBSCAN for Mobile Robot. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; Volume 2216, p. 012009. [CrossRef]
  29. Asyaky, M.S.; Mandala, R. Improving the Performance of HDBSCAN on Short Text Clustering by Using Word Embedding and UMAP. In Proceedings of the 2021 8th International Conference on Advanced Informatics: Concepts, Theory and Applications (ICAICTA), Bandung, Indonesia, 29–30 September 2021; pp. 1–6. [CrossRef]
  30. Liu, J.; Sun, S.; Chen, C. Big data Analysis of Regional Meteorological Observation Based : On Hierarchical Density Clustering Algorithm HDBSCAN. In Proceedings of the 2021 2nd International Seminar on Artificial Intelligence, Networking and Information Technology (AINIT), Shanghai, China, 15–17 October 2021; pp. 111–116. [CrossRef]
  31. Alexopoulos, E.C. Introduction to multivariate regression analysis. Hippokratia 2010, 14, 23. [PubMed]
  32. Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer ; John Wiley & Sons, Ltd.: West Sussex, UK, 2008

作者：
香港科技大学机械及航空航天工程系助理教授Rhea Liem教授
香港科技大学机械及航空航天工程系博士生Jefry YANTO先生

学术编辑： Xavier Olive

收文日期：2022 年 8 月 25 日
接受日期：2022 年 10 月 17 日
出版日期：2022 年 10 月 20 日

出版人说明：MDPI 对于出版地图的司法管辖权主张和所属机构关系保持中立。


版权所有：© 2022。作者保留版权。被许可人瑞士巴塞尔 MDPI。本文章乃根据共享创意特许条款 (CC BY) (https://creativecommons.org/licenses/by/4.0/) 分发的开放取览文章。

關鍵字：飛機燃料模型；主成分分析；基於分層密度之噪聲應用空間聚類法；多元線性迴歸法

2023年6月