一枚硬币连续掷出五次正面，同一条路线的列车在同一天发生了两宗意外，或是随机播放清单连续给你三首由相同歌手演唱的歌曲。这似乎并不是巧合，但真正的随机也许未如我们想像中的那样。
统计上独立的事件：硬币并没有记性！
让我们先从硬币说起。掷一枚公平的硬币（fair coin）时，很多人会预期正面和反面朝上的结果会交替出现，连续掷出正面大概会使我们目瞪口呆。在没有细想之下，你可能也会估计正面和反面出现的次数会各占一半，所以如果正面出现的比例多于一半时，反面应该就将会出现得更频密来补偿之前不均的结果 — 当然，这个想法是错误的，因为硬币并不会记得先前的结果！如果你有一枚公平的硬币，它连续掷出了99次正面朝上的结果，你不能说下次会有较大机会掷出反面，因为它毕竟是一枚公平的硬币 [1]。由于每次抛掷对下次结果都没有影响，我们称这些为统计上独立的事件。
如果我们掷两次硬币，每次正面或反面朝上的机会均等，以下是四个可能的结果：正正、正反、反正和反反。每个结果发生的机会都相同（1/4），但以任何次序出现一正一反的机率为2/4而不是1/4。掷三次的话会有八种可能：正正正、正正反、正反正、正反反、反正正、反反正、反正反和反反反，每种可能的机率均为1/8。一连掷十次的话，正反正反正反正反正反、正正反正反反反反正反和反反反反反反反反反反三者的机率都一样，均为1/210或1/1024，可是会令你留下深刻印象的肯定是最后一个组合而不是其他 [2]。我们太著迷于从随机产生的结果中找规律，并会就此轻率地下结论 [3]。
现实上的洗牌演算法：Fisher–Yates洗牌法与天真法
让我们先介绍Fisher–Yates洗牌法 [2]，它根据另一组随机数字把序列随机地打乱。假设现在有一组由数字1至10组成的序列。首先从1至10选一个随机号码叫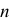 
，然后移除上述序列中第 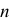个数字放到一组新序列里。之后对序列中余下的数字重复以上步骤，从1至9、1至8中选 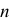，如此类推，直至序列中的所有数字都被移除（见图一）。
|
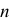原来序列 | 新序列 |
|---|---|---|
| 3 | 1 2 |
3 |
| 8 | 1 2 4 5 6 7 8 |
3 9 |
| 5 | 1 2 4 5 |
3 9 6 |
| 2 | 1 |
3 9 6 2 |
| 3 | 1 4 |
3 9 6 2 5 |
| 5 | 1 4 7 8 |
3 9 6 2 5 10 |
| 2 | 1 4 7 8 | 3 9 6 2 5 10 4 |
| 1 | 3 9 6 2 5 10 4 1 | |
| 2 | 7 |
3 9 6 2 5 10 4 1 8 |
| 1 | 3 9 6 2 5 10 4 1 8 7 |
图一 Fisher–Yates洗牌法的一例
如果 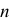的选择是随机的，那新序列也会是完全随机的。让我们来看看为甚么这个关系会成立。我们可以以一副卡牌作比喻来理解这个演算法：每次随机移除一张卡牌，并把移除的卡牌叠起来组成一副新的卡组。
把这个演算法与其他洗牌方法作比较可以突显为甚么Fisher–Yates法是真正随机。有一个「天真（naïve）」的方法是每次在卡组中取出一张卡牌，然后与另一张随机选择的卡牌交换位置，再对卡组中的每张卡重复以上步骤 [4]。换言之，如果我们用天真法洗一副有三张卡的卡组（卡牌上标记了#1、#2和#3），第一步我们会把卡组中的第一张卡与第一（不变）、第二或第三张卡的其中一张交换位置。然后到第二张卡，我们又使它与三张卡的其中一张对换位置；重复以上过程直至卡组中的每一张卡都洗过一遍。
每一步我们都随机从三张卡里面选择一张，因此三回合一共可以带来3 x 3 x 3 = 33 = 27 个排列（permutations）结果。思路清晰的你大概已经意识到我们只有3 x 2 x 1 = 6种方式来排列三张卡牌：123, 132, 213, 231, 312和321。如果你把从天真法每一步产生的可能排列逐一列出，你会发现132, 213和231出现了五次，而123, 312和321只出现四次，结果显然是偏倚的。凭直觉也能得知因为27并不能被6整除（基本上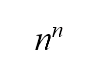 
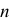或 > 2都不能被 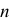! 整除），所以某些排列一定会比其他出现得更多（如果每个排列出现的机会均等，排列结果的数目应是6的倍数）。由于机会不均等，因此天真法并不随机。
这与我们平时洗扑克牌的方式相似：简单来说就是将卡组中的一叠卡牌与另一叠互换位置；可是这些方法都不会产生随机的结果，因为洗过的卡牌都继续在系统里流转。
跟Fisher–Yates法对比一下，由于每个回合都有一张卡被移除（并调到新的卡组中），所以被考虑的卡牌会越来越少，而在我们一副三张卡的例子里，三回合只会带来3 x 2 x 1 = 6个排列结果。计算这种排列结果数目的方法与计算三张卡牌有多少个排列可能性的方法一样：两者都用到阶乘函数 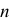! = 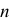x ( 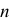– 1) … x 3 x 2 x 1；在我们的例子中是3! = 3 x 2 x 1，亦等同3P3。两者背后的计算思路基本上相同，相同之处在于列出所有可能排列的方式。因此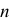， 本身的随机性在洗牌中被得以保留；这也是为甚么只要能确保 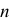是随机选出的，就能保证Fisher–Yates法能提供一个完全随机的序列。
创造不太随机但感觉随机的播放清单
现在回到我们在图一的随机序列：3-9-6-2-5-10-4-1-8-7。它是我们共有十首歌的随机播放清单：曲目一、四、七、十是Adele（艺人甲）的歌，曲目二、五、八是BTS防弹少年团（艺人乙）的歌，而曲目三、六、九是Celine Dion（艺人丙）的歌。播放清单看来是这样的：
Celine Dion ➜ Celine Dion ➜ Celine Dion ➜ BTS防弹少年团 ➜ BTS防弹少年团 ➜ Adele ➜ Adele ➜ Adele ➜ BTS防弹少年团 ➜ Adele
这样的播放清单看起来一点儿也不随机！这是因为我们不经意地聚焦在连续三首Celine Dion和Adele的歌这个不寻常的规律里。假如你是2012至2014年的Spotify用家，你也许已经急不及待去投诉 [5] 这个不给你听K-pop的该死随机播放清单（假设你在2014年前已经在听K-pop）。那年Spotify实在收到太多投诉，使他们放弃原来使用的Fisher–Yates演算法而引入新的演算法（对！他们原本是用Fisher–Yates法来产生随机播放清单 [6]）。现在选择随机播放时，演算法会确保由同一歌手演唱或属于同一种类的歌曲大致平均地分布在播放清单中 [7]。
正是Spotify工程师把播放清单弄得不再随机，来令你相信它变得更加随机。
参考资料：
- Lieberman, D. A. (2012). Human Learning and Memory. Cambridge, UK: Cambridge University Press. doi:10.1017/CBO9781139046978
作者︰香港科技大学《科言》学生编辑胡适之
设计︰香港科技大学《科言》学生设计师林晓薏
翻译︰香港科技大学《科言》总编辑刘劭行
2022年9月