A coin comes up heads five times in a row. Two accidents happen on the same train line in one day. Or a shuffled playlist plays you the same artist three times running. Sometimes it seems like something other than coincidence is at work, but true randomness may not always feel that way to us.
Statistically Independent Events: The Coin Doesn't Remember!
Let's start with the coins. Many people expect a fair coin to alternate between heads and tails and will be surprised if the coin keeps coming up heads. When you first thought about it, you might have expected heads to come up half the time and tails half the time, so if heads have come up over half the time the coin should start landing on tails more often to compensate. This isn't true, of course, because the coin can't remember this! If you have a fair coin which has just landed on heads 99 times in a row, you can't say that it's more likely to land on tails next time because it's a fair coin [1]. Since each toss has no effect on the next, we say that they are statistically independent events.
If we toss a coin twice, and each toss has an equal chance of heads (H) or tails (T), there are four possible outcomes: HH, HT, TH, TT. Each outcome has the same chance (1/4) of happening, but the chances of one head and one tail in either order are 2/4 instead of 1/4. Three times, and we have eight possible outcomes: HHH, HHT, HTH, HTT, THH, TTH, THT, and TTT, each with 1/8 probability. In a series of ten tosses, the results HTHTHTHTHT and HHTHTTTTHT and TTTTTTTTTT all have the same chance of occurring – one in 210, or 1/1024 – but you'll probably remember the last one and not the others [2]. We read too much into patterns in a random sample, and we're willing to jump to conclusions based on those patterns [3].
Shuffling in Real World: Fisher–Yates Shuffle vs. Naïve Method
Take the Fisher–Yates shuffle [2], which shuffles a sequence randomly based on the input of other random numbers. Let's say there is an existing sequence of the numbers 1 to 10. First pick a random number from 1 to 10, called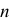 
, and remove the 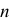th number in the existing sequence to begin a new sequence. For the next numbers, repeat this with any 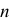from 1 to 9, from 1 to 8, and so on, until there are no numbers left in the existing sequence (see Figure 1).
|
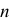Existing sequence | New sequence |
|---|---|---|
| 3 | 1 2 |
3 |
| 8 | 1 2 4 5 6 7 8 |
3 9 |
| 5 | 1 2 4 5 |
3 9 6 |
| 2 | 1 |
3 9 6 2 |
| 3 | 1 4 |
3 9 6 2 5 |
| 5 | 1 4 7 8 |
3 9 6 2 5 10 |
| 2 | 1 4 7 8 | 3 9 6 2 5 10 4 |
| 1 | 3 9 6 2 5 10 4 1 | |
| 2 | 7 |
3 9 6 2 5 10 4 1 8 |
| 1 | 3 9 6 2 5 10 4 1 8 7 |
Figure 1 An example of Fisher–Yates shuffle.
This sequence is totally random if the choices of 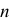are also random, and in a moment, we'll look at why this is true. We can think about the algorithm in terms of a deck of cards, removing random cards one at a time and stacking up the discarded cards in order to form a new deck.
Comparing this with other ways to shuffle cards makes it obvious why Fisher–Yates is truly random. A "naïve" method is to take each card in sequence one at a time and swap it with another randomly chosen card, repeating for every card in the deck [4]. In other words, if we shuffle three cards (marked #1, #2, and #3) using our naïve method, we first swap the first card in the sequence with either the first (unchanged), second or third card. Then we shuffle the second card with either one of the three cards, and repeat the process until we go through every position in the sequence.
The random choice at every stage is between three cards, so shuffling three times gives 3 x 3 x 3 = 33 = 27 permutations. But as you may know, there are only 3 x 2 x 1 = 6 possible ways to mix up the order of those three cards: 123, 132, 213, 231, 312, 321. If you list all possible permutations resulting from the naïve method, you will find that the combinations 132, 213 and 231 come up five times, while 123, 312 and 321 come up only four times. Obviously, the result is biased. If you think intuitively, since 27 is not divisible by 6 (and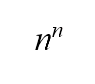 
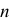or > 2 is not divisible by 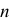! in general), some of the possible permutations must happen more often than others (if all of them are equally likely to occur, the number of shuffles will be a multiple of 6). The chances are not equal, so the naïve method is not random.
This is similar to the usual way to shuffle cards: In simple terms, we take an entire bunch of cards and swap it with another bunch of cards in the sequence. But these methods do not result in a random outcome, because the shuffled cards continue to circulate within the system.
Contrast this with Fisher–Yates. Since a card is removed from consideration after each shuffle (and gets put into a new deck), the pool to be shuffled at each stage gets smaller, and for our three-card deck there will be 3 x 2 x 1 = 6 permutations after three shuffles. Note that these permutations are calculated the same way as the possible ways of mixing up three cards: they both use the factorial function 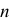! = 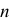x (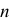 - 1) … x 3 x 2 x 1, or 3! = 3 x 2 x 1 in this case which is equivalent to 3P3. They are essentially the same algorithm in the sense that they are counted the exact same way. So the randomness behind the original selections of 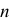is preserved throughout the permutations, and this is why we can guarantee Fisher–Yates is a fully random sequence provided n is chosen randomly.
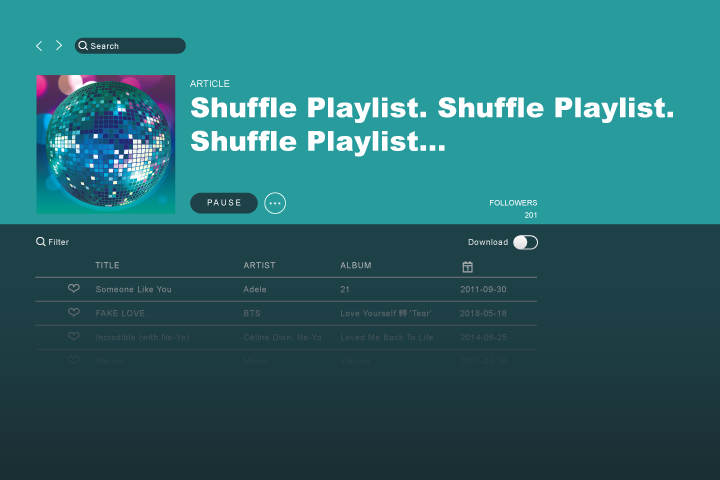
Creating a Less Random Playlist That Feels More "Random"
Now let's return to our random sequence 3-9-6-2-5-10-4-1-8-7 in Figure 1. We can call it a shuffled playlist of ten songs and say that songs 1, 4, 7, and 10 are by Adele (artist A), songs 2, 5, and 8 are by BTS (artist B), and songs 3, 6, and 9 are by Celine Dion (artist C). It looks like this:
Celine Dion ➜ Celine Dion ➜ Celine Dion ➜ BTS➜ BTS ➜ Adele ➜ Adele ➜ Adele ➜ BTS ➜ Adele
Which doesn't look random at all! That's because we focus on the unusual patterns of three Celine Dion and three Adele songs in a row. If you were like Spotify users between 2012 and 2014, you'd have rushed to complain [5] about all the times the shuffle algorithm played non-K-pop music over and over (assuming you also listened to K-pop before 2014). There were so many complaints, in fact, that Spotify retired the Fisher–Yates algorithm – yes, they originally used Fisher–Yates to shuffle playlists [6] – and introduced a new shuffling algorithm. Now, when you shuffle a playlist, different songs by the same artist and in the same genre are distributed roughly evenly across the list [7].
The Spotify engineers made the shuffle less random to convince you that it became more random.
References：
- Lieberman, D. A. (2012). Human Learning and Memory. Cambridge, UK: Cambridge University Press. doi:10.1017/CBO9781139046978
Author: Peace Foo, Student Editor, Science Focus, The Hong Kong University of Science and Technology
Design: Charley Lam, Graphic Designer, Science Focus, The Hong Kong University of Science and Technology
Translation: Daniel Lau, Managing Editor, Science Focus, The Hong Kong University of Science and Technology
September 2022