在中華國際數學建模挑戰賽（IM2C）委員會和參賽學校的協助下，我們在 7月份通訊中分享2020年度中華區賽事的其中一個賽題和得獎論文，今次我們會繼續分享賽事的另一個賽題 – 網絡新聞可信度測評。
曾經有人說過︰「真相還在穿鞋的時候，謊言可走遍半個世界。」這情形再沒有比網絡媒體時代來得更真實了。謬誤信息可以迅速觸及成千上萬乃至數百萬的讀者，全球對網絡新聞可信度的關注日益增長。網絡新聞可信度測評已成為關乎信息生態系統健康的緊迫挑戰，每一位身居其中的數碼時代公民都受到影響。IM2C將此作為基礎，為中華區中學生設立賽題。
北京市十一學校團隊以此問題的建模方案論文榮獲2020年度IM2C中華區特等獎，本文由作者從獲獎報告縮寫而成。
如果您是中學生或於中學任教並有興趣參與這項挑戰，請留意 IM2C網站 的最新資訊。
學生︰漆琪，胡琪珺，劉宇萌，宋逸東
摘要
隨著網絡時代的到來，網絡新聞的可信度衡量顯得尤為重要。本文基於邏輯謬誤數量、引用數量、非客觀人稱和標點數量，和語法錯誤數量四個指標，採用分類的方式，以109篇新聞數據為訓練集，40篇新聞數據為測試集，建立靜態模型和動態模型。最終靜態模型平均殘差為0.7625，動態模型平均殘差為0.7875。
基本假設
- 用於衡量網絡新聞可信度的每一項指標都獨立存在，不會互相影響。
- 網絡新聞的可信度不會受到文章語言的影響。
符號約定
表1：符號約定
| 實際意義 | 符號 | 單位 |
| 單位語法錯誤數量 | x | / |
| 單位邏輯謬誤數量 | y | / |
| 單位非客觀人稱和標點數量 | z | / |
| 單位引用數量 | w | / |
| 描述語法錯誤數量指標的函數 | Gr | / |
| 描述邏輯謬誤指標的函數 | Lo | / |
| 描述非客觀人稱和標點數量指標的函數 | Pp | / |
| 描述引用數量指標的函數 | Ci | / |
| 單位語法錯誤數量函數的權重 | A | / |
| 單位邏輯謬誤標誌詞函數的權重 | B | / |
| 單位非客觀人稱和標點數量之和函數的權重 | C | / |
| 單位引用數量函數的權重 | D | / |
| 模型坐標系中代表每一個新聞的點的位置向量 | V | / |
| 擬合集（用於擬合指標函數的新聞的集合） | F | / |
| 測評集（用於測評可信度的新聞的集合） | M | / |
| 權重集（用於調整坐標軸中指標函數權重的新聞的集合） | W | / |
| 專家對新聞的可信度的評分 | SE | / |
| 坐標系中被測點距已知點的距離 | d | / |
| 模型測評的新聞可信度評分 | S | / |
| 殘差（預測分和專家評分之差） | r | / |
| 平均殘差 | r | / |
模型建立
A. 建立指標框架及測量
1. 反映新聞可信度的潛在特徵
首先，本文根據新聞可信度理論，設立衡量新聞可信度的維度[1]，並確定反映這些維度的。五個維度分別是學術性、準確性、客觀性、權威性、時效性。但考慮到參考文獻中的新聞來源時間都比較久遠，但我們考量的新聞發生時間較近，而且評分都是在新聞發佈後兩周之內即時產生的，所以排除時效性。
依照餘下的四個維度，我們提出了十三個潛在指標。通過繪製文章評分與指標的關係圖，進行相關性分析，我們確定了單位語法錯誤數量、單位邏輯謬誤數量、單位非客觀人稱和標點數量以及單位引用證據數量四項檢測指標，分別衡量新聞的學術性、準確性、客觀性、權威性四個維度，這就是衡量新聞可信度的指標框架。
2. 指標的測量
由於最終要檢驗的數據是指定的40篇新聞，本文利用climatefeedback.com以及healthfeedback.com[2, 3]中未在原40篇中出現的總計109篇新聞來建立模型。對於模型框架中149條新聞的四個指標，本文分別用了以下方法進行測量：
- 將新聞正文粘貼入Grammarly網站[4] 用其較為準確的功能檢測語法錯誤檢以及總字數[5]，從而測量單位語法錯誤數量（x）。
- 訂立邏輯謬誤標誌詞庫，並檢測每篇新聞中這些詞的數量，取其與新聞總字數的比值，得到單位邏輯謬誤數量（y）。
- 檢測每篇新聞中非客觀人稱和標點數量之和，取其與新聞總字數的比值得到單位非客觀人稱和標點數量（z）。
- 訂立引用標誌詞庫，檢測每篇新聞中的數量，取其與總字數的比值得到單位引用數量（w）。
B. 靜態模型
1. 擬合函數
利用以上對於各個評判新聞可信度的指標的檢測方法對149篇新聞進行檢測後，本文通過控制變量測量各個指標分別如何影響新聞的可信度，即將其餘3個指標取值分別控制在較小的區間內並繪製散點圖（如圖1~4所示）確定第4個指標與新聞可信度評分的函數關係。我們利用Logger Pro軟件擬合出最貼切兩個變量關係，即相關性（Correlation）較大、最小二乘法（RMSE）較小的函數型，得到結果如下：
a. 描述語法錯誤數量指標的函數:
Gr(x) = -1.0019 × ln(23.910x)
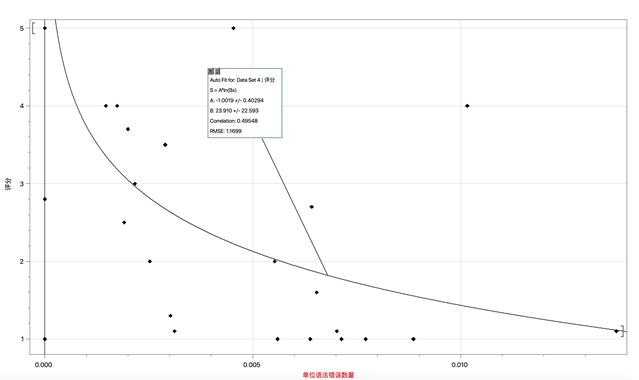
圖1：Gr的擬合
b. 描述邏輯謬誤指標的函數:
Lo(y) = -202.81y + 4.3979
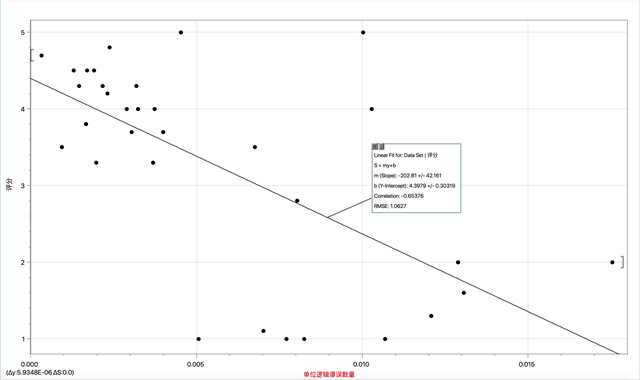
圖2：Lo的擬合
c. 描述非客觀人稱標點數量指標的函數:
Pp(z) = -0.34024 × ln(0.091420z)
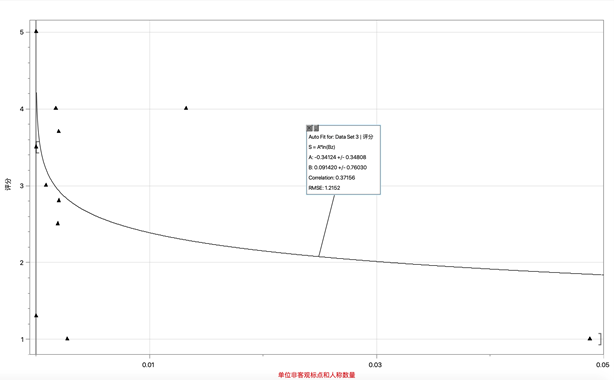
圖3：Pp的擬合
d. 描述引用數量指標的函數:
Ci(w) = 166.29w + 1.9086
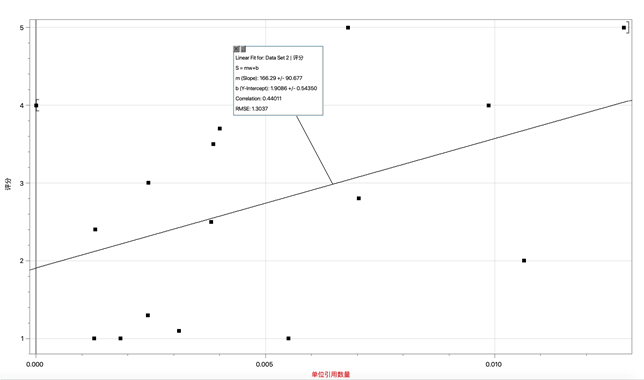
圖4：Ci的擬合
2. 建立四維坐標系、調整權重並得出可信度
在確定每個指標分別與網絡新聞可信度的函數關係後，以(0,0,0,0)為原點，四個指標分別為x,
y, z,
w軸，建立一個四維坐標系。在149篇文章中選取補充的109篇，其四個指標的分別經函數映射到Gr(xi),Lo(yi),Pp(zi),Ci(wi),
其值域均為[1,5]。這使每篇文章化為四維坐標系的一個點。設四個維度的單位向量分別為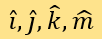
，則用序號i標記每一個被測新聞在該坐標系中對應的點，並表示它們的坐標向量和位置向量：
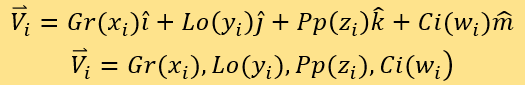
比對被測點和已知點的距離來測定分數。該坐標系的四個軸分別為A*Gr(x)、B*Lo(y)、C*Pp(z)和D*Ci(w)。定義SEi為第i個被測點的專家評分。接著，定義測評集M=擬合集F。將測評集M中的已知評分新聞所對應的點都置入坐標系。用序號j標記測評集M中新聞對應已知點，它們的坐標向量為：
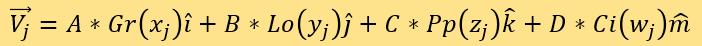
需注意，此時權重A, B, C, D還未確定。並定義SEj為j所標記的M中新聞對應已知點的專家評分。對於每一個i（被測點）和所有的j（M中的已知點），計算距離：
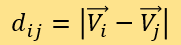
取最小的n個Dij，並將它們的標記j進一步標記為j*，通過以下公式計算出被測新聞的測評可信度Si：
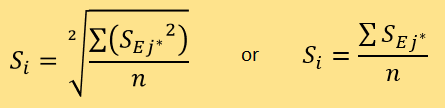
後邊靈敏性分析將分析平方平均數和算數平均數的優劣。
然後，利用以下公式計算被標記為i的新聞的測定可信度與其真實專家評分的殘差ri
和特定權重下的總體殘差
，由於本文無需對其求導：
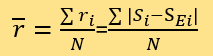
其中，N為被測數據總數。定義權重集W為所有未在擬合集F中的已知評分的新聞，並將它們當作被測新聞進行上述操作。利用python程序，找到一組使最小的權重值（A,
B, C,
D）確定為測評所使用的最優權重。最後，利用程序求出需要被測的新聞（本文為檢驗模型，使用指定的40篇伴有SEi的新聞）的Si以及（在非檢驗性的測評中沒有SEi和）。
C. 動態模型
動態模型在靜態模型的基礎上添加了學習機制，使被測點（用i標記）能在對其的測評完成後成為測評點（用j標記）。具體操作為當權重確定後，每一個Si被計算出時，將i所標記的點對應的新聞置入測評集M，再進行下一篇被測新聞可信度的測評，最後求出Si以及。
模型求解
A. 靜態模型
採取算數平均數計算Si，根據python程序的計算，得到的最佳權重為{A=0.4,
B=0.9, C=0.01,
D=0.6}。預測結果的殘差包括15個ri=0.0，2個ri=0.5，16個ri=1.0，1個ri=1.5及6個ri=2.0。計算可得：
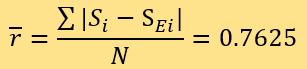
採取平方平均數的方法計算Si，最佳權重為{A=2.7, B=3.3, C=0.01,
D=0.01}。預測結果的殘差包括15個ri=0.0，2個ri=0.5，16個ri=1.0，1個ri=1.5以及6個ri=2.0。計算可得：
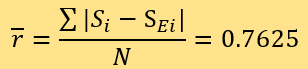
所以，用兩種方法測評的新聞可信度與專家評分的平均殘差均為0.7625。
B. 動態模型
通過程序計算，模型最佳權重為{A=1.5, B=0.6, C=4.8,
D=2.4}。預測結果的殘差包括16個ri=0.0，3個ri=0.5，13個ri=1.0，7個ri=2.0以及1個ri=3.0，計算可得：
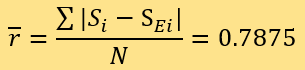
模型分析
A. 結果分析
本文在建立模型前，先用Mathematica提供的隨機森林算法對40篇新聞進行了測評，平均殘差為1.45。對比靜態模型的平均殘差0.7625以及動態模型的平均殘差0.7875可以得知，本文原創模型的靜態、動態兩個版本都能得到平均殘差大約只有隨機森林一半的測評結果，做出較好的預測。在這兩個版本之中，靜態模型的預測效果更加優秀。
B. 優缺點分析
第一個優點是它的結果很精准，用平方平均數計算評分時靜態和動態模型的平均誤差都控制在了0.8以內，小於單位分值1。
然後是它擁有權重機制，可以依據不同情景下的需要調整不同指標的重要性。
本模型的缺點是靜態模型在訓練時需要較大的已知集，否則其容錯率比較低。由以上優缺點可知，動態模型更適合在初始時即有大量可信度已知的新聞並且在後期時測評需求很大、有大量可信度未知的新聞能供其學習時使用。
C. 模型改進 – 部落尋找判定法
模型的判定方式是將坐標系中已知可信度新聞數據點按其到被測新聞坐標點距離從小到大排序，並將排序中前一定數目的點所代表的新聞的可信度求平均再四捨五入得到測評結果。然而，通過實際測評本文發現，五個分數的新聞實際形成了多於五個“部落”，即坐標空間中同一個分數的新聞形成了多個分離的區域。本文舉例說明這種現象可能帶來的問題：假設代表已知可信度為3分的新聞的數據點形成了兩個相距較遠的“部落”。當一篇新聞處於其中一個時，其按現實情況應被算為3分。然而，由於它與另一個“部落”中的3分新聞距離過遠，而5分的新聞又恰巧在它不遠處形成了一整個“部落”，它被算為了5分。針對我們發現的這個問題，我們可以改進為訓練靜態模型之前，先用k-means算法進行聚類。我們原本認為這樣訓練的結果會更好。
但是實現此改進方案後，我們發現結果不見得更佳。將k-means的k值設定為3後，我們得到的平均誤差是0.87，反而多出了14%。我們認為造成這種情況的原因是已知評分的新聞量太少，而且在各分數上分佈不均，這就導致了k-means聚類的效果不好。
靈敏性分析
控制其他參數時，我們使用參數改變前後的的變化率來測量靈敏性，計算式為：
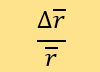
第一個參數為n，也就是被測點進入坐標系後，模型選取距該點前n近的點來決定該點分數。我們發現，當????變化28%時，變化16%。當????約為總訓練集大小的20%時，可以找到最優。
第二個參數為權重的枚舉步長，我們發現改變權重的枚舉步長對求最優權重的影響較小，因此可以適當加大步長，提高時間效率。
結論
本文全面地考慮了衡量網絡新聞可信度的五個維度，並運用統計確定了包含與可信度有關的四個指標的指標框架，恰好涵蓋了被排除的時效性以外的四個維度。
本文運用合理以及經驗證的測量方法測量了框架中的指標，並使用了原創模型的靜、動態兩個版本分別測評了指定的40篇新聞的可信度。儘管受到較小的樣本量的限制，但本文靜態、動態模型將測評值與專家評分間的平均殘差分別控制到了0.7625和0.7875。其中，原創模型的靜態模型給出的結果尤為精准，而動態模型在數據量大時有很大潛力。本文利用部落尋找判定法改進模型後，發現結果並未提升。
本文模型的意義在於開發了一套幾乎不需人力測量的指標來測評本身極為複雜的新聞可信度，從而讓出版商、社交媒體平臺和公眾能夠方便而準確地瞭解一篇新聞是否可信。由此，本文不但可以讓新聞受眾接受更加真實有效的信息，而且能引導社會對於新聞可信度本質影響因素的討論，產生巨大的社會效益。如果本文能把研究對象擴展到科學性新聞以外的其他新聞種類，可以使模型的適用範圍更加寬廣。
參考文獻
- Cassidy, William P. “Online News Credibility: An Examination of the Perceptions of Newspaper Journalists.” Journal of Computer-Mediated Communication, vol. 12, no. 2, 2007, pp. 478–498. ResearchGate, doi:10.1111/j.1083-6101.2007.00334.x.
- “Scientific Feedbacks.” Climate Feedback, https://climatefeedback.org/feedbacks/.
- “Scientific Feedbacks.” Health Feedback, https://healthfeedback.org/feedbacks/.
- “Write Your Best with Grammarly.” Grammarly, http://www.grammarly.com/.
- Collins, Bryan. “Grammarly Review: Is This Grammar Checker Worth It?” Become a Writer Today, 1 Nov. 2019, https://becomeawritertoday.com/grammar-checker-review-grammarly/#How_Effective_is_Grammarly_for_Proofreading_English
2020年9月