在中华国际数学建模挑战赛（IM2C）委员会和参赛学校的协助下，我们在 7月份通讯中分享2020年度中华区赛事的其中一个赛题和得奖论文，今次我们会继续分享赛事的另一个赛题 – 网络新闻可信度测评。
曾经有人说过︰「真相还在穿鞋的时候，谎言可走遍半个世界。」这情形再没有比网络媒体时代来得更真实了。谬误信息可以迅速触及成千上万乃至数百万的读者，全球对网络新闻可信度的关注日益增长。网络新闻可信度测评已成为关乎信息生态系统健康的紧迫挑战，每一位身居其中的数码时代公民都受到影响。IM2C将此作为基础，为中华区中学生设立赛题。
北京市十一学校团队以此问题的建模方案论文荣获2020年度IM2C中华区特等奖，本文由作者从获奖报告缩写而成。
如果您是中学生或于中学任教并有兴趣参与这项挑战，请留意 IM2C网站 的最新资讯。
学生︰漆琪，胡琪珺，刘宇萌，宋逸东
摘要
随着网络时代的到来，网络新闻的可信度衡量显得尤为重要。本文基于逻辑谬误数量、引用数量、非客观人称和标点数量，和语法错误数量四个指标，采用分类的方式，以109篇新闻数据为训练集，40篇新闻数据为测试集，建立静态模型和动态模型。最终静态模型平均残差为0.7625，动态模型平均残差为0.7875。
基本假设
- 用于衡量网络新闻可信度的每一项指标都独立存在，不会互相影响。
- 网络新闻的可信度不会受到文章语言的影响。
符号约定
表1：符号约定
| 实际意义 | 符号 | 单位 |
| 单位语法错误数量 | x | / |
| 单位逻辑谬误数量 | y | / |
| 单位非客观人称和标点数量 | z | / |
| 单位引用数量 | w | / |
| 描述语法错误数量指标的函数 | Gr | / |
| 描述逻辑谬误指标的函数 | Lo | / |
| 描述非客观人称和标点数量指标的函数 | Pp | / |
| 描述引用数量指标的函数 | Ci | / |
| 单位语法错误数量函数的权重 | A | / |
| 单位逻辑谬误标志词函数的权重 | B | / |
| 单位非客观人称和标点数量之和函数的权重 | C | / |
| 单位引用数量函数的权重 | D | / |
| 模型坐标系中代表每一个新闻的点的位置向量 | V | / |
| 拟合集（用于拟合指标函数的新闻的集合） | F | / |
| 测评集（用于测评可信度的新闻的集合） | M | / |
| 权重集（用于调整坐标轴中指标函数权重的新闻的集合） | W | / |
| 专家对新闻的可信度的评分 | SE | / |
| 坐标系中被测点距已知点的距离 | d | / |
| 模型测评的新闻可信度评分 | S | / |
| 残差（预测分和专家评分之差） | r | / |
| 平均残差 | r | / |
模型建立
A. 建立指标框架及测量
1. 反映新闻可信度的潜在特征
首先，本文根据新闻可信度理论，设立衡量新闻可信度的维度[1]，并确定反映这些维度的。五个维度分别是学术性、准确性、客观性、权威性、时效性。但考虑到参考文献中的新闻来源时间都比较久远，但我们考量的新闻发生时间较近，而且评分都是在新闻发布后两周之内即时产生的，所以排除时效性。
依照余下的四个维度，我们提出了十三个潜在指标。通过绘制文章评分与指标的关系图，进行相关性分析，我们确定了单位语法错误数量、单位逻辑谬误数量、单位非客观人称和标点数量以及单位引用证据数量四项检测指标，分别衡量新闻的学术性、准确性、客观性、权威性四个维度，这就是衡量新闻可信度的指标框架。
2. 指标的测量
由于最终要检验的数据是指定的40篇新闻，本文利用climatefeedback.com以及healthfeedback.com[2, 3]中未在原40篇中出现的总计109篇新闻来建立模型。对于模型框架中149条新闻的四个指标，本文分别用了以下方法进行测量：
- 将新闻正文粘贴入Grammarly网站[4] 用其较为准确的功能检测语法错误检以及总字数[5]，从而测量单位语法错误数量（x）。
- 订立逻辑谬误标志词库，并检测每篇新闻中这些词的数量，取其与新闻总字数的比值，得到单位逻辑谬误数量（y）。
- 检测每篇新闻中非客观人称和标点数量之和，取其与新闻总字数的比值得到单位非客观人称和标点数量（z）。
- 订立引用标志词库，检测每篇新闻中的数量，取其与总字数的比值得到单位引用数量（w）。
B. 静态模型
1. 拟合函数
利用以上对于各个评判新闻可信度的指标的检测方法对149篇新闻进行检测后，本文通过控制变量测量各个指标分别如何影响新闻的可信度，即将其余3个指标取值分别控制在较小的区间内并绘制散点图（如图1~4所示）确定第4个指标与新闻可信度评分的函数关系。我们利用Logger Pro软件拟合出最贴切两个变量关系，即相关性（Correlation）较大、最小二乘法（RMSE）较小的函数型，得到结果如下：
a. 描述语法错误数量指标的函数:
Gr(x) = -1.0019 × ln(23.910x)
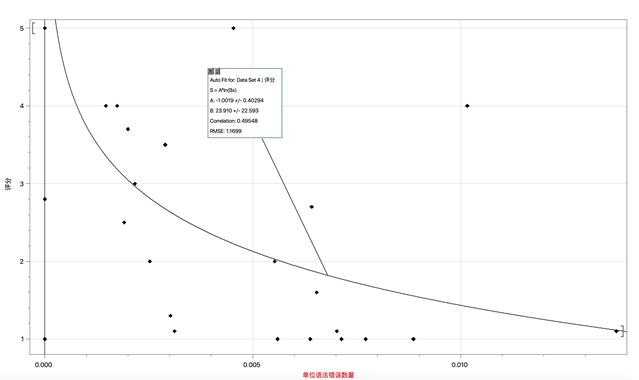
图1：Gr的拟合
b. 描述逻辑谬误指标的函数:
Lo(y) = -202.81y + 4.3979
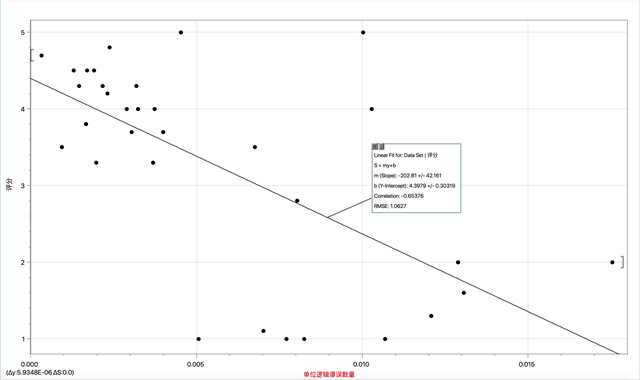
图2：Lo的拟合
c. 描述非客观人称标点数量指标的函数:
Pp(z) = -0.34024 × ln(0.091420z)
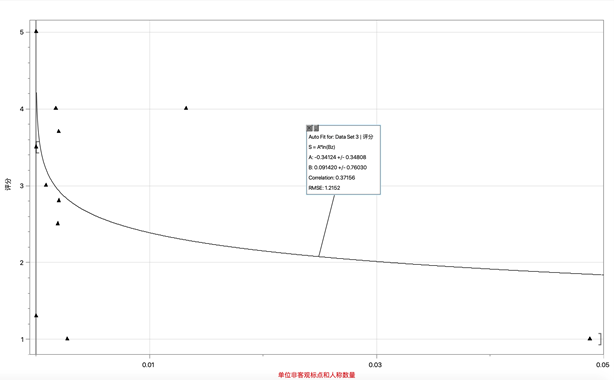
图3：Pp的拟合
d. 描述引用数量指标的函数:
Ci(w) = 166.29w + 1.9086
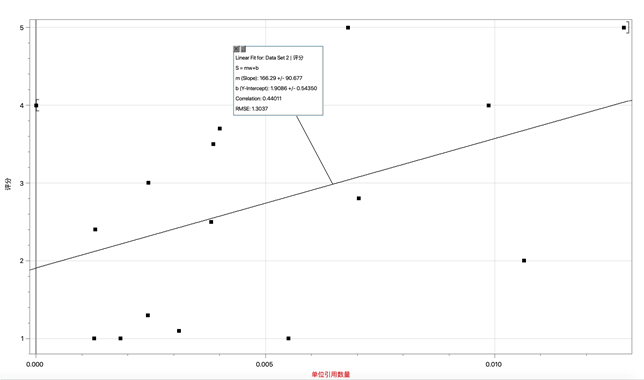
图4：Ci的拟合
2. 建立四维坐标系、调整权重并得出可信度
在确定每个指标分别与网络新闻可信度的函数关系后，以(0,0,0,0)为原点，四个指标分别为x,
y, z,
w轴，建立一个四维坐标系。在149篇文章中选取补充的109篇，其四个指标的分别经函数映射到Gr(xi),Lo(yi),Pp(zi),Ci(wi),
其值域均为[1,5]。这使每篇文章化为四维坐标系的一个点。设四个维度的单位向量分别为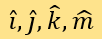
，则用序号i标记每一个被测新闻在该坐标系中对应的点，并表示它们的坐标向量和位置向量：
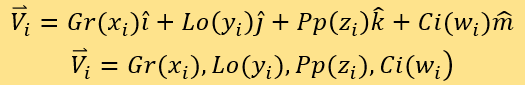
比对被测点和已知点的距离来测定分数。该坐标系的四个轴分别为A*Gr(x)、B*Lo(y)、C*Pp(z)和D*Ci(w)。定义SEi为第i个被测点的专家评分。接着，定义测评集M=拟合集F。将测评集M中的已知评分新闻所对应的点都置入坐标系。用序号j标记测评集M中新闻对应已知点，它们的坐标向量为：
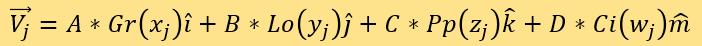
需注意，此时权重A, B, C, D还未确定。并定义SEj为j所标记的M中新闻对应已知点的专家评分。对于每一个i（被测点）和所有的j（M中的已知点），计算距离：
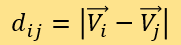
取最小的n个Dij，并将它们的标记j进一步标记为j*，通过以下公式计算出被测新闻的测评可信度Si：
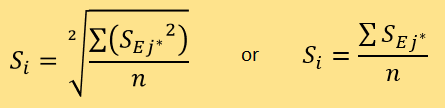
后边灵敏性分析将分析平方平均数和算数平均数的优劣。
然后，利用以下公式计算被标记为i的新闻的测定可信度与其真实专家评分的残差ri
和特定权重下的总体残差
，由于本文无需对其求导：
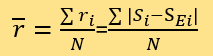
其中，N为被测数据总数。定义权重集W为所有未在拟合集F中的已知评分的新闻，并将它们当作被测新闻进行上述操作。利用python程序，找到一组使最小的权重值（A,
B, C,
D）确定为测评所使用的最优权重。最后，利用程序求出需要被测的新闻（本文为检验模型，使用指定的40篇伴有SEi的新闻）的Si以及（在非检验性的测评中没有SEi和）。
C. 动态模型
动态模型在静态模型的基础上添加了学习机制，使被测点（用i标记）能在对其的测评完成后成为测评点（用j标记）。具体操作为当权重确定后，每一个Si被计算出时，将i所标记的点对应的新闻置入测评集M，再进行下一篇被测新闻可信度的测评，最后求出Si以及。
模型求解
A. 静态模型
采取算数平均数计算Si，根据python程序的计算，得到的最佳权重为{A=0.4,
B=0.9, C=0.01,
D=0.6}。预测结果的残差包括15个ri=0.0，2个ri=0.5，16个ri=1.0，1个ri=1.5及6个ri=2.0。计算可得：
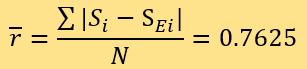
采取平方平均数的方法计算Si，最佳权重为{A=2.7, B=3.3, C=0.01,
D=0.01}。预测结果的残差包括15个ri=0.0，2个ri=0.5，16个ri=1.0，1个ri=1.5以及6个ri=2.0。计算可得：
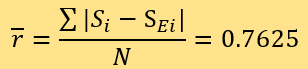
所以，用两种方法测评的新闻可信度与专家评分的平均残差均为0.7625。
B. 动态模型
通过程序计算，模型最佳权重为{A=1.5, B=0.6, C=4.8,
D=2.4}。预测结果的残差包括16个ri=0.0，3个ri=0.5，13个ri=1.0，7个ri=2.0以及1个ri=3.0，计算可得：
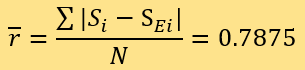
模型分析
A. 结果分析
本文在建立模型前，先用Mathematica提供的随机森林算法对40篇新闻进行了测评，平均残差为1.45。对比静态模型的平均残差0.7625以及动态模型的平均残差0.7875可以得知，本文原创模型的静态、动态两个版本都能得到平均残差大约只有随机森林一半的测评结果，做出较好的预测。在这两个版本之中，静态模型的预测效果更加优秀。
B. 优缺点分析
第一个优点是它的结果很精准，用平方平均数计算评分时静态和动态模型的平均误差都控制在了0.8以内，小于单位分值1。
然后是它拥有权重机制，可以依据不同情景下的需要调整不同指标的重要性。
本模型的缺点是静态模型在训练时需要较大的已知集，否则其容错率比较低。由以上优缺点可知，动态模型更适合在初始时即有大量可信度已知的新闻并且在后期时测评需求很大、有大量可信度未知的新闻能供其学习时使用。
C. 模型改进 – 部落寻找判定法
模型的判定方式是将坐标系中已知可信度新闻数据点按其到被测新闻坐标点距离从小到大排序，并将排序中前一定数目的点所代表的新闻的可信度求平均再四舍五入得到测评结果。然而，通过实际测评本文发现，五个分数的新闻实际形成了多于五个“部落”，即坐标空间中同一个分数的新闻形成了多个分离的区域。本文举例说明这种现象可能带来的问题：假设代表已知可信度为3分的新闻的数据点形成了两个相距较远的“部落”。当一篇新闻处于其中一个时，其按现实情况应被算为3分。然而，由于它与另一个“部落”中的3分新闻距离过远，而5分的新闻又恰巧在它不远处形成了一整个“部落”，它被算为了5分。针对我们发现的这个问题，我们可以改进为训练静态模型之前，先用k-means算法进行聚类。我们原本认为这样训练的结果会更好。
但是实现此改进方案后，我们发现结果不见得更佳。将k-means的k值设定为3后，我们得到的平均误差是0.87，反而多出了14%。我们认为造成这种情况的原因是已知评分的新闻量太少，而且在各分数上分布不均，这就导致了k-means聚类的效果不好。
灵敏性分析
控制其他参数时，我们使用参数改变前后的的变化率来测量灵敏性，计算式为：
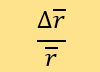
第一个参数为n，也就是被测点进入坐标系后，模型选取距该点前n近的点来决定该点分数。我们发现，当????变化28%时，变化16%。当????约为总训练集大小的20%时，可以找到最优。
第二个参数为权重的枚举步长，我们发现改变权重的枚举步长对求最优权重的影响较小，因此可以适当加大步长，提高时间效率。
结论
本文全面地考虑了衡量网络新闻可信度的五个维度，并运用统计确定了包含与可信度有关的四个指标的指标框架，恰好涵盖了被排除的时效性以外的四个维度。
本文运用合理以及经验证的测量方法测量了框架中的指标，并使用了原创模型的静、动态两个版本分别测评了指定的40篇新闻的可信度。尽管受到较小的样本量的限制，但本文静态、动态模型将测评值与专家评分间的平均残差分别控制到了0.7625和0.7875。其中，原创模型的静态模型给出的结果尤为精准，而动态模型在数据量大时有很大潜力。本文利用部落寻找判定法改进模型后，发现结果并未提升。
本文模型的意义在于开发了一套几乎不需人力测量的指标来测评本身极为复杂的新闻可信度，从而让出版商、社交媒体平台和公众能够方便而准确地了解一篇新闻是否可信。由此，本文不但可以让新闻受众接受更加真实有效的信息，而且能引导社会对于新闻可信度本质影响因素的讨论，产生巨大的社会效益。如果本文能把研究对象扩展到科学性新闻以外的其他新闻种类，可以使模型的适用范围更加宽广。
参考文献
- Cassidy, William P. “Online News Credibility: An Examination of the Perceptions of Newspaper Journalists.” Journal of Computer-Mediated Communication, vol. 12, no. 2, 2007, pp. 478–498. ResearchGate, doi:10.1111/j.1083-6101.2007.00334.x.
- “Scientific Feedbacks.” Climate Feedback, https://climatefeedback.org/feedbacks/.
- “Scientific Feedbacks.” Health Feedback, https://healthfeedback.org/feedbacks/.
- “Write Your Best with Grammarly.” Grammarly, http://www.grammarly.com/.
- Collins, Bryan. “Grammarly Review: Is This Grammar Checker Worth It?” Become a Writer Today, 1 Nov. 2019, https://becomeawritertoday.com/grammar-checker-review-grammarly/#How_Effective_is_Grammarly_for_Proofreading_English
2020年9月