我們在“大眾與科學”中曾介紹國際數學建模挑戰賽(IM2C)。這是一項面向全球中學生的國際性新型數學建模競賽。在中華國際數學建模挑戰賽委員會和參賽學校的協助下,我們很高興與大家分享2020年度中華區賽事的其中一個賽題(智能水務數據分析)和得獎論文。
水是人們日常生活中不可或缺的一部分,為了用戶的利益,我們需要一個高效能的水力運輸系統。然而在供水系統中,一些系統故障的情況,如水管或閥門故障,很容易導致漏水問題。因此,工程師和研究人員正不斷尋找各種方法去建構智能水務系統令供水更為有效。所以,電磁流量計多用於量度水流和檢查漏水情況。如詳細分析一個地區裡的水輸入和輸出量的差異,從而清楚反映水流狀態和潛在的漏水風險。儘管當今有許多數據分析方法可供使用,但一些挑戰仍然存在。國際數學建模挑戰賽(IM2C)便將此挑戰為基礎為中華區中學生設立賽題。
為秉持所有IM2C的賽題均來自現實世界之特色,香港應用科技研究院(ASTRI)專家從他們的實際研發項目來創設此賽題。賽題原文及包含 8 個不同虛擬區域中輸入和輸出水流量之差的數據集可見於此。
香港的拔萃女書院團隊以此問題的建模方案論文榮獲2020年度IM2C中華區特等獎,本文由作者從獲獎報告縮寫而成。
如果您是中學生或於中學任教並有興趣參與這項挑戰,請留意IM2C網站的最新資訊。
學生:林慧心, 蘇泳潼, 黃嘉愈, 余瑞琦
指導教師:楊寶琪
我們先分析數據模式,並指出鑑定異常水流的準則。我們發現在已給8個地區的數據波動普遍很大,沒有明顯的規律。但水輸入和輸出量的差異(簡稱實際數值)徘徊於-12和24之間。我們斷定細小的水流波動由人們每天用水量的細微轉變導致,而較大的水流波動則因異常水流而致。
在已給8個地區的水輸入和輸出量差異中,我們根據其相對數據集計算8個模型函數。藉此可預測各地區的水流趨勢,從而檢測異常水流和漏水情況。R2數值測量了模型函數的準確度。如果R2 > 0.5,該模型函數會被視為一個好模型(正如很多科學家所指)。數值越近 1,模型函數便越準確。由於這 8 個地區的R2數值都小於 0.5,可見這些數據都極為分散,且沒有直接關係。
識別異常的第一個標準是考慮每天的實際值,這方法可以於短時間內發現問題,如實值超出正常範圍的5%,則被列為異常,並將此現象歸類為嚴重漏水問題。
第二個標準是總出水量突然變化。通過計算 5 個連續點的平均斜率,我們可找到變化的幅度。如果斜率超過正常斜率範圍的5%,則為異常。這可幫助我們發現較小的漏水問題,因為那個點可能並未超出正常範圍,但它顯示出惡化的趨勢,所以如果不加注意,它可能會變成更嚴重的漏水問題。
然後我們根據數據分析結果,開發一個通用的數學模型對 8 個虛擬區域進行異常值檢測。
第一個方法是找出實際數值的正常範圍。
我們先找出數據中心簡單移動平均數。我們設第x天的實際數值為Ax。由於用來計算首7天和最後7天(第1-7, 94–100天)的中心簡單移動平均值的數據不足以計算15天的中位數,因此這些日子需另作計算。否則計算第x天的移動平均值便會通過此公式計算:( Ax-7 + Ax-6 + ... + Ax + Ax+6 + Ax+7 ) / 15 . 首7天的中心簡單移動平均值的公式是 ( A1 + A2 + A3 + ... + A2x-1 ) / ( 2x -1 ) ; 最後7天的中心簡單移動平均值的公式是 ( A2x-100 + ... + A98 + A99 + A100 ) / ( 201 - 2x ) .
然後我們使用以下公式計算移動方差:
移動方差 = (實際值(x) - 實際值的平均值)2的移動平均值
計算移動標準偏差值的公式:
移動標準偏差 = 移動方差的平方根
上限 = 實際值的移動平均值 + 2 x 移動標準偏差值
下限 = 實際值的移動平均值 - 2 x 移動標準偏差值
下圖為其中已給地區7的正常值域數據:
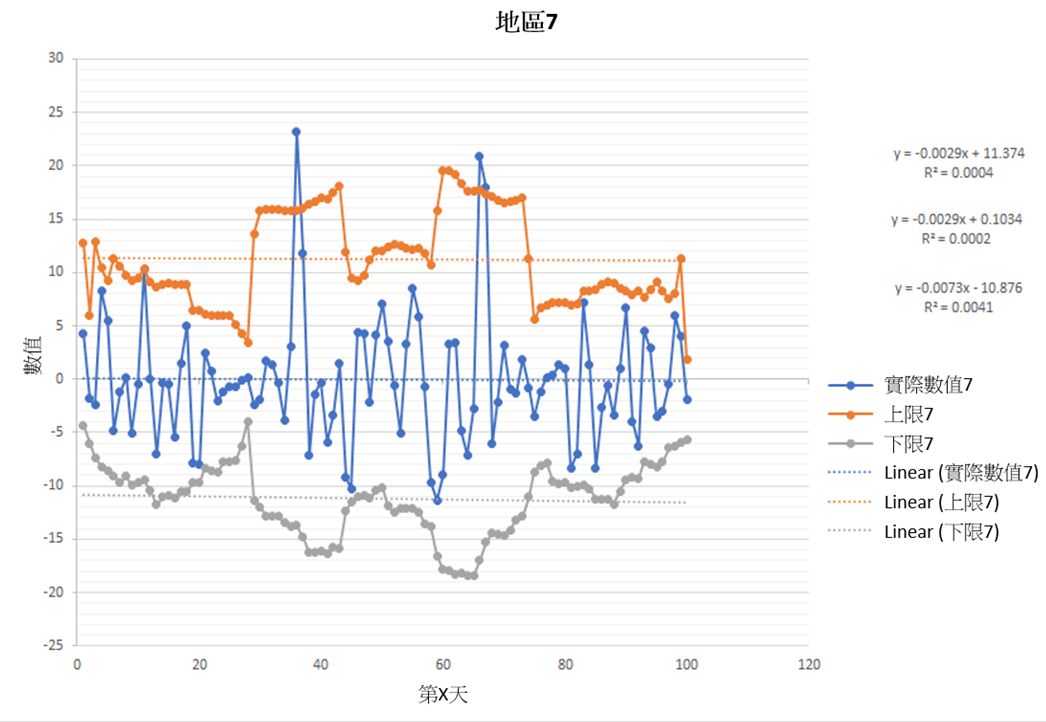
移動標準偏差值會被乘以2因為它包含約95% 數據,這意味著約5% 數據不在正常值域裡,它們被認定為異常。由於不同區域有不同的移動平均線,因此每個區域的移動標準偏差根據相應的數據和水流情況方面是不同的,必須單獨計算。
移動平均值允許我們分析數據的趨勢,而不是分析個别數據。這是因為我們需要比較不同的數據來確定水流是否異常,並且還可以讓我們預測水流的趨勢。我們還使用了較長的移動平均值(每個間隔15天),這可以消除短期的水流波動並突出長遠的趨勢從而簡化計算。此外,使用奇數的間隔有助簡化檢查過程。我們只需要在數據中找一個數字,看看它是否與計算出的平均值相差很大即可,有助於減少發生異常的可能性。
計算移動平均值可以用簡單移動平均法和累積移動平均法計算,但我們只使用了簡單移動平均法。這是因為它只參考最近期的數據,並且可以更迅速地發現異常現象。相反,累積移動平均值參考的數據是由第一天開始計算。第x天 (CMAx) 的累積移動平均值的計算算式是 ( A1 + A2 + ... + Ax ) / x , 第x天的實際值以 Ax代表。第x + 1天的累積移動平均值的計算算式即是 ( Ax+1 + x(CMAx)) / ( x+1 ) 。如果數據集中有異常數據,我們未必能迅速發現,這是因為在這個方法中,有大量的數據被列入考慮。因此,即使我們發現了有異常數據,它也未必完全可信,因為這可能被其他先前多個異常數據累積而影響。而且,由於日子的數量是雙數,即 100,我們不可能找到一個整數中間數。因此,我們選擇了用中心簡單移動平均法,此方法會於已計算的移動平均值再取之平均值,則能使已計算的移動平均值更平滑和從中找出一個中間數。
我們的第二種方法是計算數據的正常斜率值域。
圖表上的每個斜率都代表著一定天數內水輸入和輸出量之間的差異的變化。因水輸入量維持一樣,所以當圖表上的一個數值異於前一個時,可見出水量就會發生變化。因此,我們可以使用斜率來衡量出水量增加或減少的幅度。如上所述,用簡單標準偏差計算,當5個連續點的平均斜率在該區的實際值模型函數之上,即大於數據正常範圍,就被認為是一個總出水量大幅減小的情況,反之亦然。
我們選擇了5個連續數據進行計算,因為如果我們考慮太少數據,就不能準確認定水流是否由於其他因素(如電磁流量計的故障),而出現異常情況。同時,若考慮太多數據,將降低發現異常漏水問題的效率,從而無法在漏水問題變得嚴重前發送警告信號。因此,我們考慮了5個數據。
為了計算數據的正常斜率範圍,我們首先找出每5個連續數據之間的平均斜率,然後計算它們的平均值。然後,我們使用以下公式計算值的方差:
方差 = (實際值 - 實際值的平均值)2的平均值
接著,我們通過計算出方差的平方根來計算簡單標準偏差。
然後使用以下公式計算斜率範圍:
正常斜率範圍的上限 = 實際斜率平均值 + 2 x 簡單標準偏差
正常斜率範圍的下限 = 實際斜率平均值 - 2 x 簡單標準偏差
就如移動標準偏差,簡單標準偏差必須乘以2,才能覆蓋正常數據的95%。因此剩餘的5% 被視為異常。
下圖為已給地區7的正常斜率值域數據:
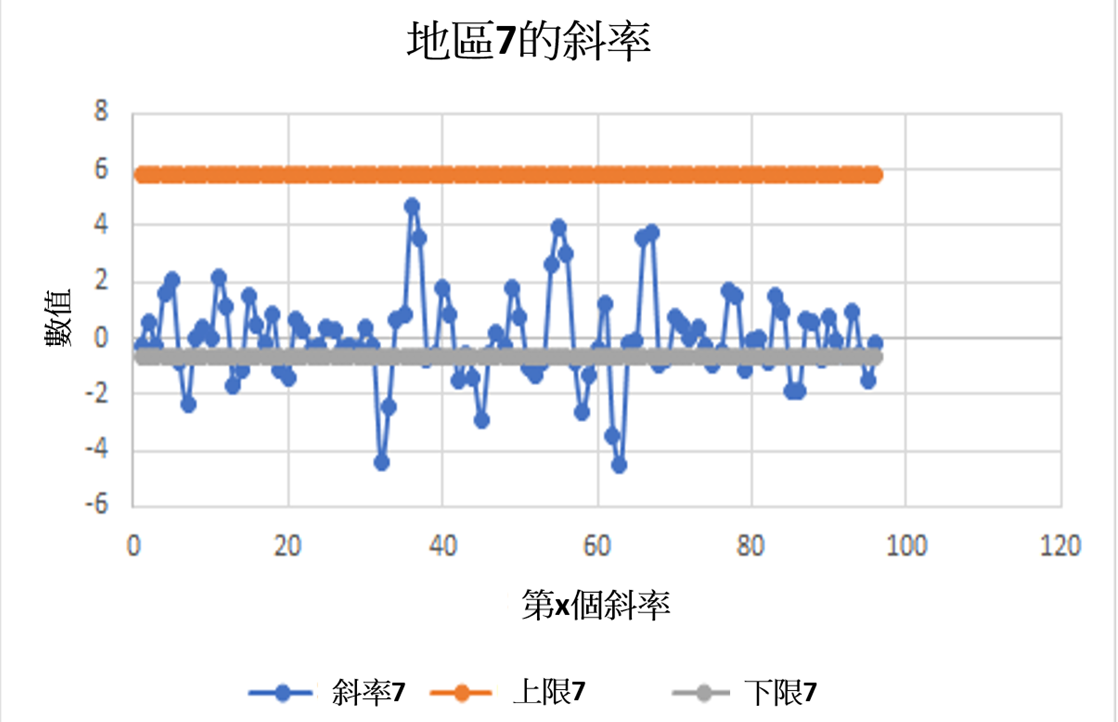
設計完數學模型後,我們對兩種方法進行了比較。使用數據正常範圍的方法運用了移動平均值,這樣可以減少其他因素造成的影響,包括電磁流量計的故障。(當中降噪量等於計算平均值時所考慮的數據量的平方值,即是15的平方根)。我們還可以更快地檢測到異常。
相反,正常斜率範圍的方法是通過簡單標準偏差來計算的,它花費的時間更少,並且可以檢測到更多的異常情況,繼而發現更多細微的錯誤,更頻繁地提醒人們和防止將來出現嚴重的漏水問題。
我們將8個區域的數據存儲到一個Excel檔案中,並使用Python編程檢查異常情況,以便計算所需的數字(如移動標準偏差、斜率等)。使用Python程式亦有助我們快速、清晰地檢測異常情況,容易找出流水量異常的情況,亦即超出數據正常範圍或數據斜率正常範圍的日子。
設計數學模型後,我們根據數據測試了模型,亦評估了模型的優勢和局限。
這個數學模型的優勢之一,就是它能夠讓人更有效地檢測水流的異常情況。當電磁流量計檢測到任何水流異常,便可以立即將信號傳送到供水系統,提醒及警告人們盡快修理水管或供水系統,從而可以防止漏水問題惡化。
另外,我們的模型非常易於使用。我們只需要下載 Excel檔案,並輸入區域號碼,就可以迅速在數據中找到異常點。這讓我們能夠在短時間內識別漏水問題,從而進一步提高供水系統的效率和效力。
最後,我們的數學模型能夠非常全面地檢測水流異常。我們通過兩種方法檢測異常水流:計算數據的正常範圍和數據斜率的正常範圍,這既能檢測嚴重的漏水問題,又能找出輕微的漏水現象。
可是,我們的數學模型也有一個局限。由於每個區域的人口眾多,在較小的水管分支裡,水輸入和輸出量差異不大,因此我們無法檢測到當中異常的水流,也就忽略了較小的水管分支中的漏水問題。
總括而言,我們建立了一個能夠同時了解多個流量計的數學模型及有效地檢測流量異常的情況,並 (1)分析了數據模式並找出識別數據異常的標準,(2)建立了通用的數學模型,根據數據分析的結果對8個虛擬區域進行了異常水流量的檢測,以及 (3)根據數據測試我們建設的數學模型,然後就模型和異常檢測的結果做出解釋。我們希望透過提醒供水機構和大眾關於漏水的情況,防止潛在故障惡化,避免公眾面臨的嚴重漏水問題。
參考
- Variance: Simple Definition, Step by Step Examples https://www.statisticshowto.datasciencecentral.com/probability-and-statistics/variance/
- Standard Deviation https://www.statisticshowto.datasciencecentral.com/probability-and-statistics/variance/
- What is R-squared https://www.displayr.com/what-is-r-squared/
- Bell Curve and Normal Distribution Definition https://www.thoughtco.com/bell-curve-normal-distribution-defined-2312350
- Moving Average https://www.investopedia.com/terms/m/movingaverage.asp
- Calculating standard deviation step by step https://www.khanacademy.org/math/statistics-probability/summarizing-quantitative-data/variance-standard-deviation-population/a/calculating-standard-deviation-step-by-step
- Moving Averages and Simple Moving Averages http://www.informit.com/articles/article.aspx?p=2433607&seqNum=2
- Cumulative Moving Average https://qkdb.wordpress.com/2013/05/11/cumulative-moving-average/
- Calculating standard deviation step by step https://www.khanacademy.org/math/statistics-probability/summarizing-quantitative-data/variance-standard-deviation-population/a/calculating-standard-deviation-step-by-step
- Moving Averages and Centered Moving Averages https://www.mathsisfun.com/data/standard-deviation.html
- Standard Deviation and Variance https://www.mathsisfun.com/data/standard-deviation.html
- Bell Curve and Normal Distribution Definition https://www.thoughtco.com/bell-curve-normal-distribution-defined-2312350
- Moving Average Filters https://www.analog.com/media/en/technical-documentation/dsp-book/dsp_book_Ch15.pdf
2020年7月