研究背景︰
研究背景︰動理學模型在很多重要領域都被廣泛應用，例如稀薄氣體，等離子物理，天文物理，以及一些新興領域例如半導體設置，環境、社會和生物科學。動理學模型描述的是由大量粒子組成的空氣系統的動態演變，其解描述的是某個時刻，粒子出現在某個空間位置，以某個速度運動的概率。在多尺度物理模型的框架中，動理學模型在原子和連續模型之間建立了橋樑。下圖描繪了空氣動理學模型在從微觀到宏觀的多尺度物理模型中的位置：
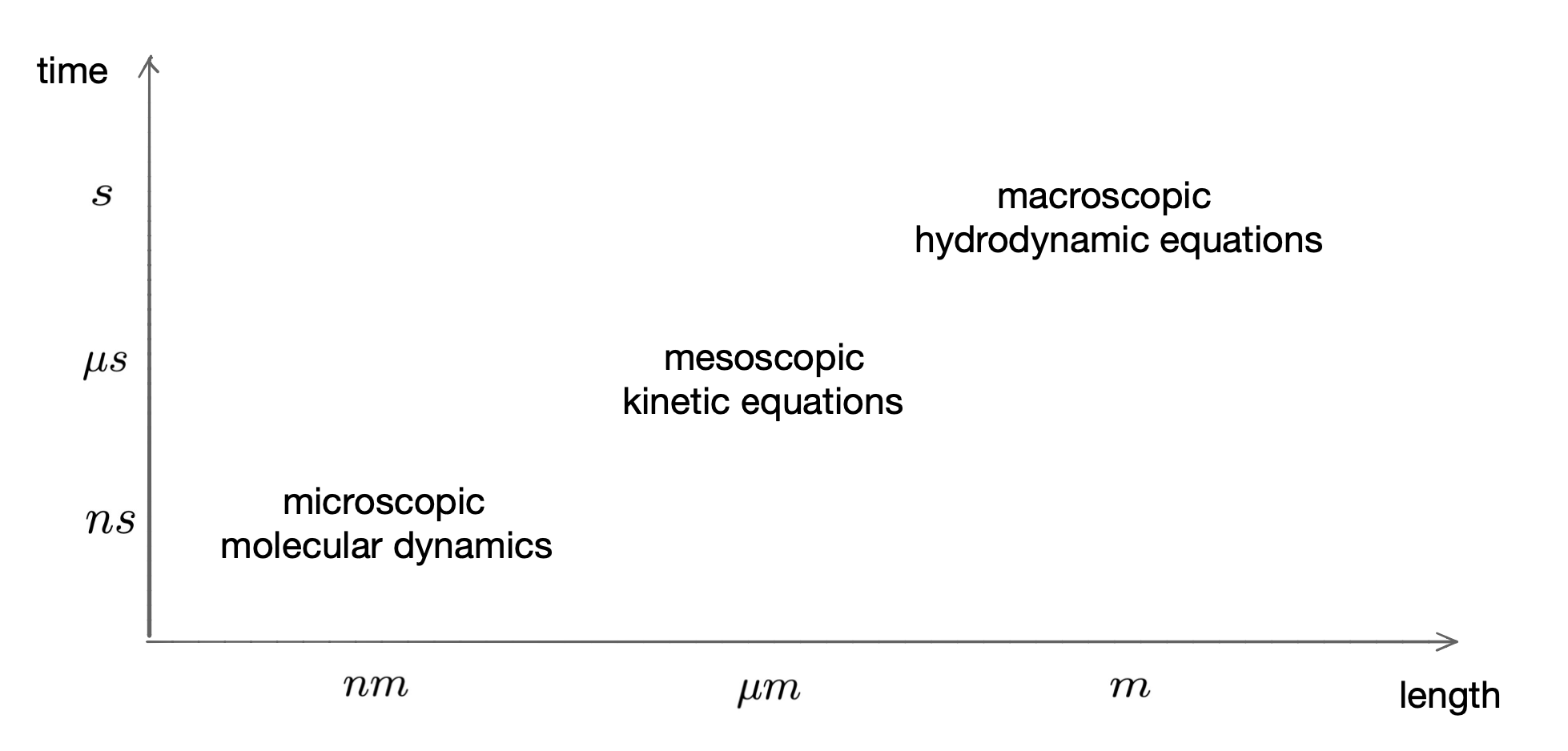
圖1︰多尺度下的物理模型
玻爾茲曼方程在1872 年被路德維希-玻爾茲曼發現，是動理學物理中最重要的模型之一。它是一個帶有積分和微分算子的方程，描述了單原子稀薄氣體粒子之間的二元碰撞和空間運動。歷史上，人們在理論和數值計算方面已經對玻爾茲曼方程做出大量研究。它的方程形式如下：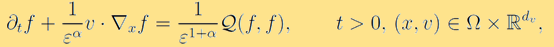 
這裡函數 
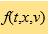描述了時間t，粒子在空間位置 
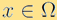，以速度 
運動，而被找到的概率。努特生數 
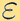是一個無量綱的平均自由徑，描述了空氣的稀薄程度；常數 
代表了不同尺度。方程的右端 是一個積分算子，刻畫了粒子之間的二元碰撞，形式為：
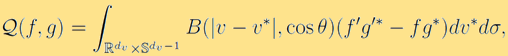這裡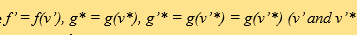 
是碰撞後的速度)和符號 
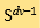表示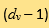 
維的單位球。碰撞核 
是一個非負函數，描述了粒子碰撞的互相作用機制。
至於動理學的應用，舉例來說，稀薄氣體的動理學在航空航天探索中無處不在。受上世紀五六十年代的太空探索項目的推動，世界各地的科學家在中和及離子化的流體學的理論和實驗研究方面取得了突破進展。這本書[1] 介紹了過去幾十年玻爾茲曼方程和稀薄氣體動理學的發展。 太空項目中，研究重返載具周圍的氣流是一項很重要的應用，例如動理加熱，衛星阻力和能量的平衡，火箭在極端高度和太空中操作時的排氣量，設計高空大氣的發聲裝置，極端高度的氣雲，等等。玻爾茲曼方程在其他領域也有廣泛而重要的應用，例如航天物理，等離子體物理，粒子加速器和半導體裝置的設計，等等。
幾個挑戰:
不確定量化(UQ)，在過去十幾年是應用數學備受關注的熱點話題。量化模型中的不確定因素對於模型的評估、驗證及提高其準確度起著重要的作用，並可以讓人們得到更有說服力的模型輸出值的預期以及更好的風險評估與管理。如下的表格展示了不確定量化問題的重要因素和步驟： 另一方面，動理學方程，經常是由N 體牛頓方程通過平均場論極限所推導出來，典型的動理學方程右端含有描述粒子之間碰撞的積分算子。對於複雜的系統，精確算出碰撞核幾乎是不可能的，因此實踐中一般採用的是通過試驗得出的公式，這就帶來了不確定因素。其他可能的不確定因素的來源包括初值或邊界值，外力作用的不精確測量。這些隨機性為設計動理學方程有效的數值方法帶來挑戰，對於高維問題也會帶來維數災難。動理學方程的不確定量化課題，直到最近幾年開始得到關注和發展。
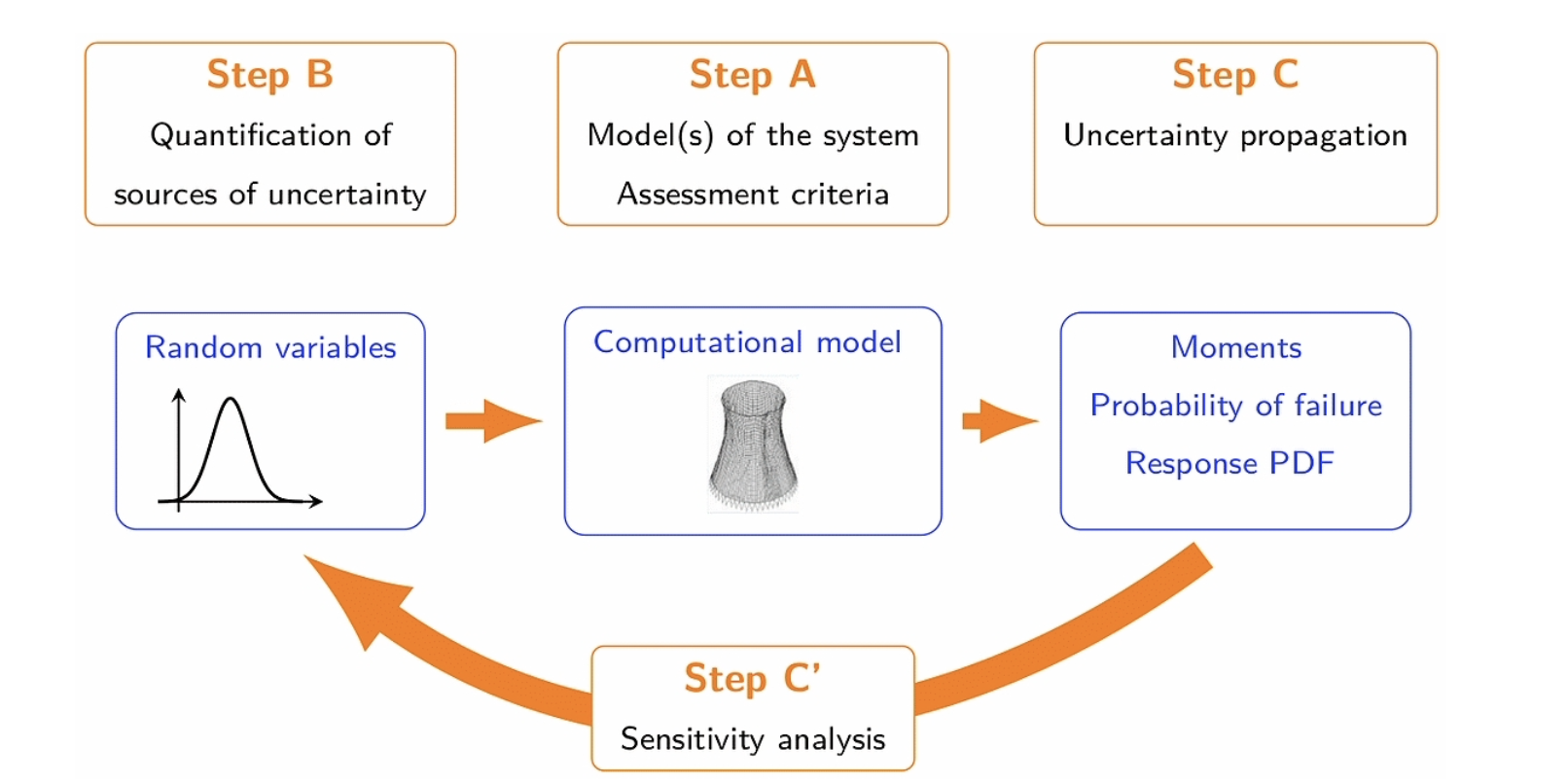
圖2: 解決不確定量化問題的一般機制，圖片來自[6]。
不確定量化中的一類非侵入式的方法叫做隨機搭配(SC) 方法。對於這類方法，一個關鍵的挑戰是數值計算的成本，特別是對於高維的複雜問題。SC 方法通過對確定問題的數值算法在隨機空間採樣後重複很多遍計算，因此整體的計算成本很高，可能無法解決現實中的複雜問題。幸運的是，對於現實中的物理問題，經常存在一些模擬近似、更簡單的模型。與高保真模型相比，這些模型或許描述了模型背後簡化了的物理原理，或是數值計算格式中使用了更稀疏的網格。儘管它們的精確度不一定高，但是它們通常可以解決或捕捉到物理模型中的重要性質或現象，並作出值得信賴、可以量化的輸出值預估。對於動理學方程不確定量化問題上，人們借助這種簡化模型設計出多保真方法，並在這一領域取得重要進展。
圖3: 高維不確定量化問題的挑戰：高計算成本。
動理學方程的另一個主要的挑戰是模型中經常有時間和空間的多尺度問題，我們用努特生數 來刻畫，它可以在一個計算區域中有顯著不同數量級的跨越，涵蓋從流體，到中間過渡及稀薄氣體不同的尺度。漸近保持算法(AP) [2] 提供了一種有效的處理這類問題的方法，在過去二十多年被動理學方程和雙曲方程等領域廣泛應用。我們將其主要思想總結在下圖中，細節可以參照[2]。總結來說，AP 算法在數值離散的層面上，做到了微觀模型和宏觀模型之間的漸近保持，並且無需在數值離散中針對小的努特生數值妥協，因此顯著降低了數值格式的計算成本。
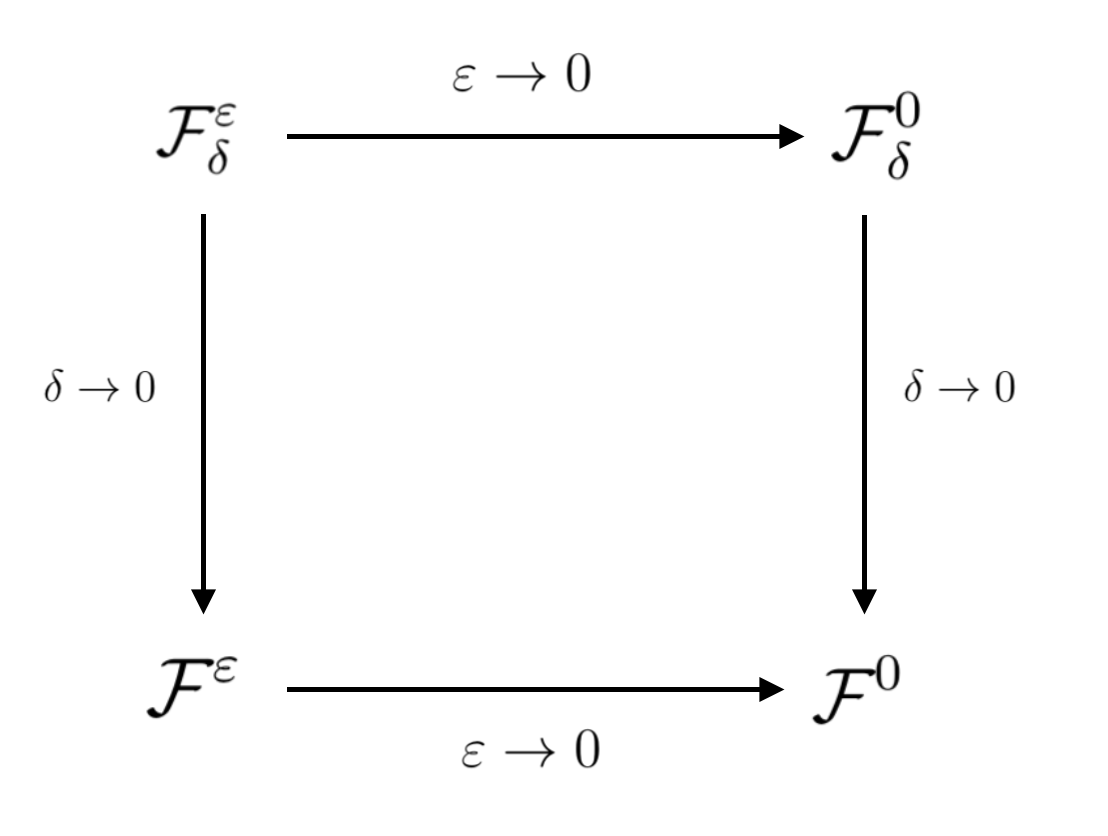
圖4: AP 算法的核心思想[2]。
幾個結果：
1. 分析
Hypocoercivity 理論是研究動理學方程的穩定性和長時間解的表現的一個重要工具。根據[7]，研究逸散微分方程（例如模型(1)）涉及(i) 退化的逸散算子；(ii) 保守的流運算子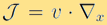 
二者的結合帶來了方程解收斂到唯一的平衡穩態。這套偏微分方程的理論核心是構造一個特殊的李雅普諾夫函數，可以證明與索伯列夫范數等價並且隨著時間演變指數收斂到零。
偏微分方程的局部敏感度分析是研究模型輸出的解對於隨機輸入參數是否敏感。通過學習對應的確定問題的hypocoercivity 理論，我們將其拓展到不確定量化問題上來。在[4] 這篇文獻，我們研究了一類線性和非線性的帶一般碰撞算子的動理學方程，對於帶有隨機初值和隨機碰撞核的動理學問題，特別是玻爾茲曼方程，基於合理的一些參數假設，我們建立了一套完整的關於方程解的正則性和長時間下的表現。這套理論適用於一般的多尺度帶碰撞項的動理學方程的不確定量化問題，包括玻爾茲曼方程、朗道方程，以及半古典量子玻爾茲曼和線性運動方程等。該方向的研究可以參照這本書[3]。
2. 數值方法
我們致力於研究解決多尺度動理學方程不確定量化問題的高效數值方法，並在這一領域取得突破性進展。概括來說，我們總結以下幾種[5] 提到的主要方法：
對於多尺度動理學方程不確定量化問題，我們已經在分析和數值方法方面取得重要進展，並計劃在未來繼續致力於該領域的跨學科發展和拓展更廣泛的應用。
參考文獻:
[1] C. CERCIGNANI, The Boltzmann equation in the whole space, in The Boltzmann Equation and Its Applications, Springer, 1988, pp. 40–103. [2] S. JIN, Efficient asymptotic-preserving (AP) schemes for some multiscale kinetic equations, SIAM Journal on Scientific Computing, 21 (1999), pp. 441–454. [3] S. JIN AND L. PARESCHI, eds., Uncertainty quantification for hyperbolic and kinetic equations, vol. 14 of SEMA SIMAI Springer Series, Springer, Cham, 2017. [4] L. LIU AND S. JIN, Hypocoercivity based sensitivity analysis and spectral convergence of the stochastic Galerkin approximation to collisional kinetic equations with multiple scales and random inputs, Multiscale Model. Simul., 16 (2018), pp. 1085–1114. [5] L. PARESCHI, An introduction to uncertainty quantification for kinetic equations and related problems, (2020). [6] B. SUDRET, Uncertainty propagation and sensitivity analysis in mechanical models–contributions to structural reliability and stochastic spectral methods, Habilitationà diriger des recherches, Université Blaise Pascal, Clermont-Ferrand, France, (2007). [7] C. VILLANI, Hypocoercivity, Mem. Amer. Math. Soc., (2009).
作者︰ 香港中文大學數學系助理教授劉鎏教授 2021年3月