研究背景︰
研究背景︰动理学模型在很多重要领域都被广泛应用,例如稀薄气体,等离子物理,天文物理,以及一些新兴领域例如半导体设置,环境、社会和生物科学。动理学模型描述的是由大量粒子组成的空气系统的动态演变,其解描述的是某个时刻,粒子出现在某个空间位置,以某个速度运动的概率。在多尺度物理模型的框架中,动理学模型在原子和连续模型之间建立了桥梁。下图描绘了空气动理学模型在从微观到宏观的多尺度物理模型中的位置:
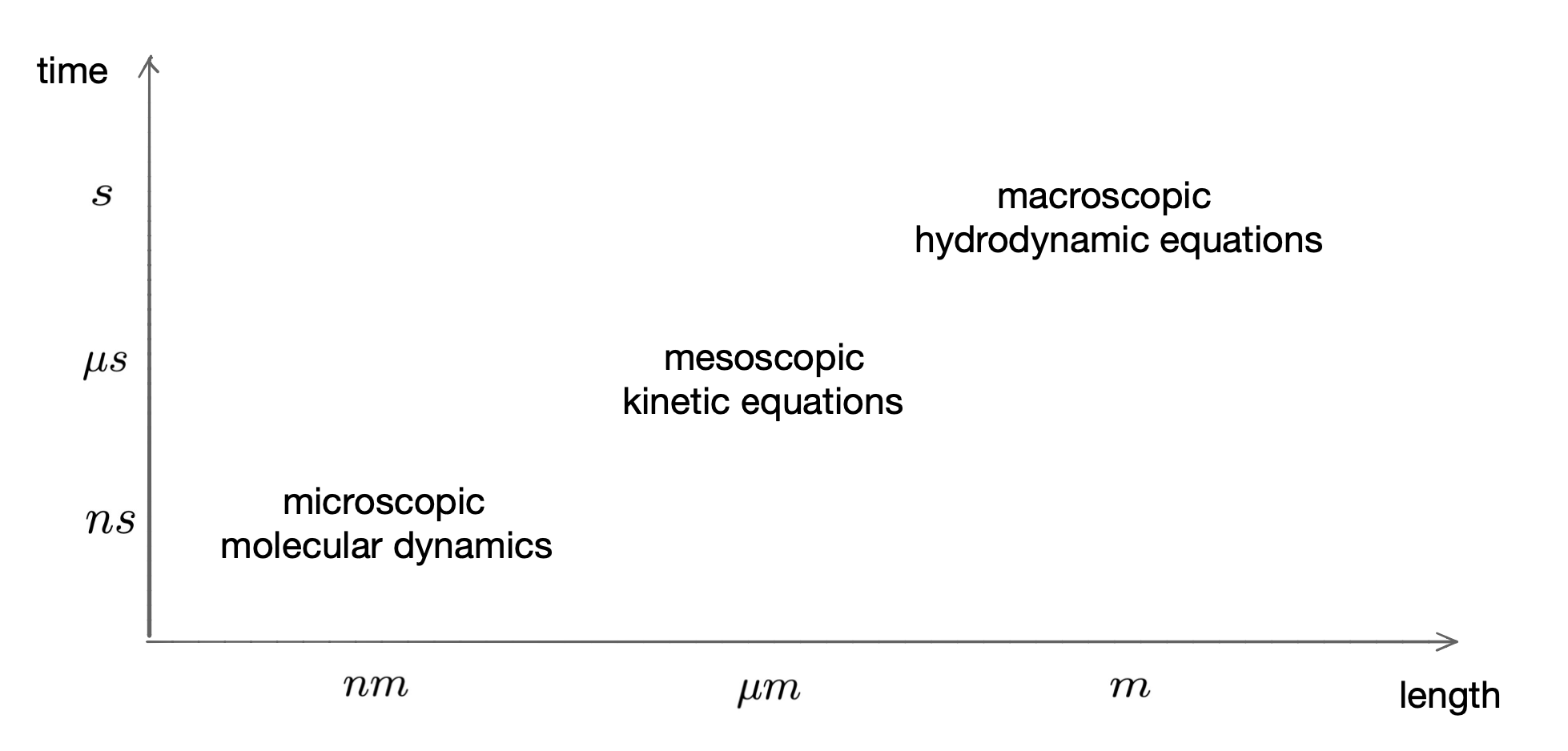
图1︰多尺度下的物理模型
玻尔兹曼方程在1872 年被路德维希-玻尔兹曼发现,是动理学物理中最重要的模型之一。它是一个带有积分和微分算子的方程,描述了单原子稀薄气体粒子之间的二元碰撞和空间运动。历史上,人们在理论和数值计算方面已经对玻尔兹曼方程做出大量研究。它的方程形式如下: 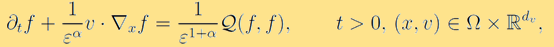 这里函数
这里函数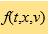 描述了时间t,粒子在空间位置< img src="/images/science_in_the_community/Liu_Liu/equation_03.png">,以速度
描述了时间t,粒子在空间位置< img src="/images/science_in_the_community/Liu_Liu/equation_03.png">,以速度 运动,而被找到的概率。努特生数
运动,而被找到的概率。努特生数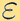 是一个无量纲的平均自由径,描述了空气的稀薄程度;常数
是一个无量纲的平均自由径,描述了空气的稀薄程度;常数
 是一个积分算子,刻画了粒子之间的二元碰撞,形式为:
是一个积分算子,刻画了粒子之间的二元碰撞,形式为:
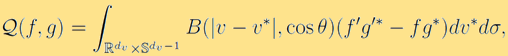 这里
这里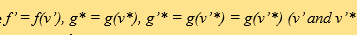 是碰撞后的速度)和符号
是碰撞后的速度)和符号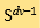 表示
表示 维的单位球。碰撞核
维的单位球。碰撞核  是一个非负函数,描述了粒子碰撞的互相作用机制。
是一个非负函数,描述了粒子碰撞的互相作用机制。
至于动理学的应用,举例来说,稀薄气体的动理学在航空航天探索中无处不在。受上世纪五六十年代的太空探索项目的推动,世界各地的科学家在中和及离子化的流体学的理论和实验研究方面取得了突破进展。这本书[1] 介绍了过去几十年玻尔兹曼方程和稀薄气体动理学的发展。 太空项目中,研究重返载具周围的气流是一项很重要的应用,例如动理加热,卫星阻力和能量的平衡,火箭在极端高度和太空中操作时的排气量,设计高空大气的发声装置,极端高度的气云,等等。玻尔兹曼方程在其他领域也有广泛而重要的应用,例如航天物理,等离子体物理,粒子加速器和半导体装置的设计,等等。

几个挑战:
不确定量化(UQ),在过去十几年是应用数学备受关注的热点话题。量化模型中的不确定因素对于模型的评估、验证及提高其准确度起着重要的作用,并可以让人们得到更有说服力的模型输出值的预期以及更好的风险评估与管理。如下的表格展示了不确定量化问题的重要因素和步骤: 另一方面,动理学方程,经常是由N 体牛顿方程通过平均场论极限所推导出来,典型的动理学方程右端含有描述粒子之间碰撞的积分算子。对于复杂的系统,精确算出碰撞核几乎是不可能的,因此实践中一般采用的是通过试验得出的公式,这就带来了不确定因素。其他可能的不确定因素的来源包括初值或边界值,外力作用的不精确测量。这些随机性为设计动理学方程有效的数值方法带来挑战,对于高维问题也会带来维数灾难。动理学方程的不确定量化课题,直到最近几年开始得到关注和发展。
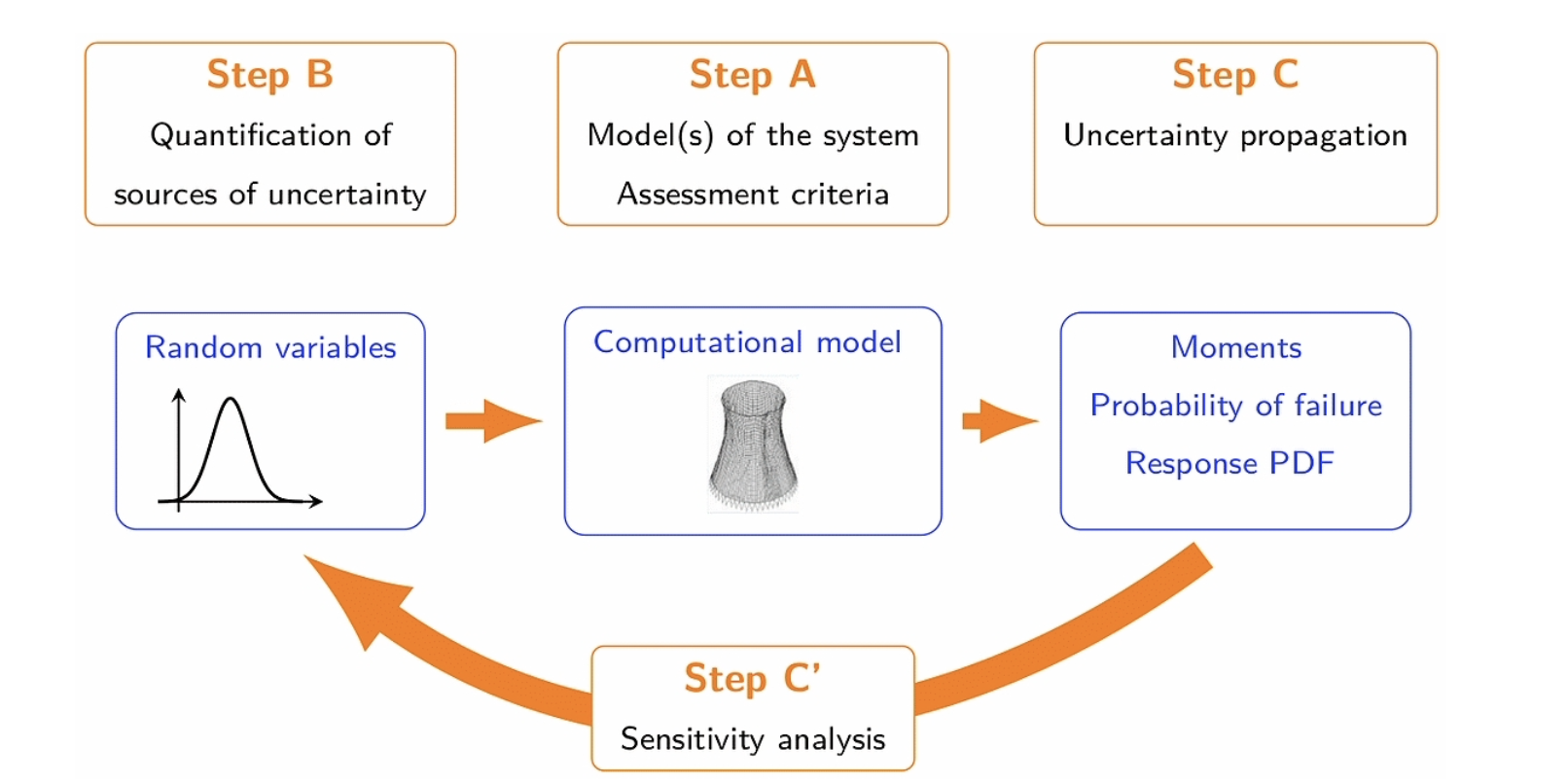
图2: 解决不确定量化问题的一般机制,图片来自[6]。
不确定量化中的一类非侵入式的方法叫做随机搭配(SC) 方法。对于这类方法,一个关键的挑战是数值计算的成本,特别是对于高维的复杂问题。 SC 方法通过对确定问题的数值算法在随机空间采样后重复很多遍计算,因此整体的计算成本很高,可能无法解决现实中的复杂问题。幸运的是,对于现实中的物理问题,经常存在一些模拟近似、更简单的模型。与高保真模型相比,这些模型或许描述了模型背后简化了的物理原理,或是数值计算格式中使用了更稀疏的网格。尽管它们的精确度不一定高,但是它们通常可以解决或捕捉到物理模型中的重要性质或现象,并作出值得信赖、可以量化的输出值预估。对于动理学方程不确定量化问题上,人们借助这种简化模型设计出多保真方法,并在这一领域取得重要进展。
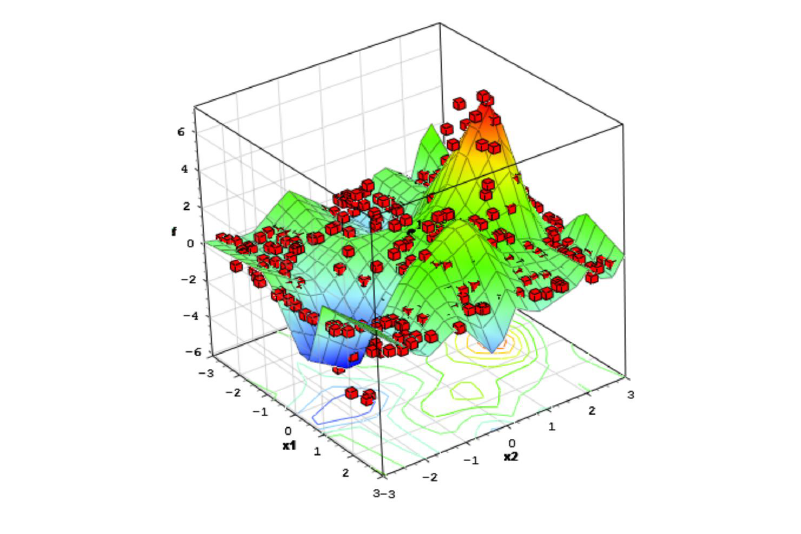
图3: 高维不确定量化问题的挑战:高计算成本。
动理学方程的另一个主要的挑战是模型中经常有时间和空间的多尺度问题,我们用努特生数来刻画,它可以在一个计算区域中有显著不同数量级的跨越,涵盖从流体,到中间过渡及稀薄气体不同的尺度。渐近保持算法(AP) [2] 提供了一种有效的处理这类问题的方法,在过去二十多年被动理学方程和双曲方程等领域广泛应用。我们将其主要思想总结在下图中,细节可以参照[2]。总结来说,AP 算法在数值离散的层面上,做到了微观模型和宏观模型之间的渐近保持,并且无需在数值离散中针对小的努特生数值妥协,因此显著降低了数值格式的计算成本。
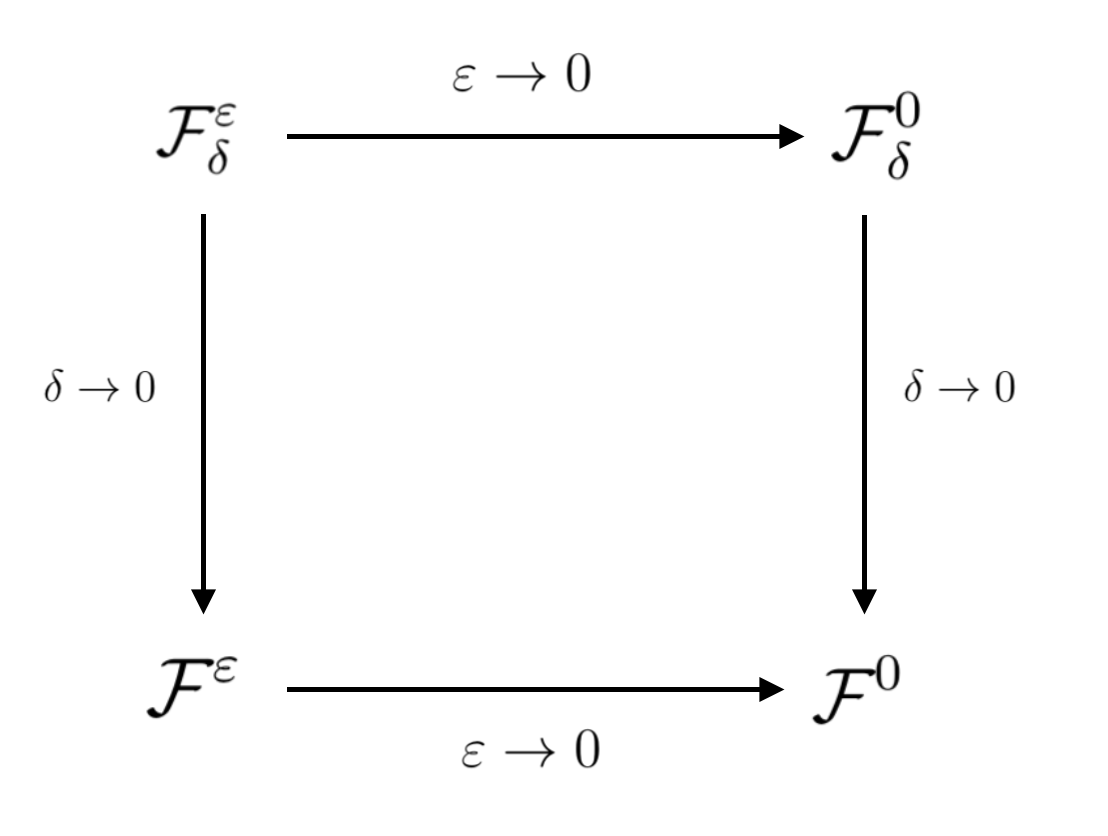
图4: AP 算法的核心思想[2]。
几个结果:
1. 分析
Hypocoercivity 理论是研究动理学方程的稳定性和长时间解的表现的一个重要工具。根据[7],研究逸散微分方程(例如模型(1))涉及(i) 退化的逸散算子;(ii) 保守的流运算子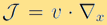 二者的结合带来了方程解收敛到唯一的平衡稳态。这套偏微分方程的理论核心是构造一个特殊的李雅普诺夫函数,可以证明与索伯列夫范数等价并且随着时间演变指数收敛到零。
二者的结合带来了方程解收敛到唯一的平衡稳态。这套偏微分方程的理论核心是构造一个特殊的李雅普诺夫函数,可以证明与索伯列夫范数等价并且随着时间演变指数收敛到零。
偏微分方程的局部敏感度分析是研究模型输出的解对于随机输入参数是否敏感。通过学习对应的确定问题的hypocoercivity 理论,我们将其拓展到不确定量化问题上来。在[4] 这篇文献,我们研究了一类线性和非线性的带一般碰撞算子的动理学方程,对于带有随机初值和随机碰撞核的动理学问题,特别是玻尔兹曼方程,基于合理的一些参数假设,我们建立了一套完整的关于方程解的正则性和长时间下的表现。这套理论适用于一般的多尺度带碰撞项的动理学方程的不确定量化问题,包括玻尔兹曼方程、朗道方程,以及半古典量子玻尔兹曼和线性运动方程等。该方向的研究可以参照这本书[3]。
2. 数值方法
我们致力于研究解决多尺度动理学方程不确定量化问题的高效数值方法,并在这一领域取得突破性进展。概括来说,我们总结以下几种[5] 提到的主要方法:
对于多尺度动理学方程不确定量化问题,我们已经在分析和数值方法方面取得重要进展,并计划在未来继续致力于该领域的跨学科发展和拓展更广泛的应用。
参考文献:
[1] C. CERCIGNANI, The Boltzmann equation in the whole space, in The Boltzmann Equation and Its Applications, Springer, 1988, pp. 40–103. [2] S. JIN, Efficient asymptotic-preserving (AP) schemes for some multiscale kinetic equations, SIAM Journal on Scientific Computing, 21 (1999), pp. 441–454. [3] S. JIN AND L. PARESCHI, eds., Uncertainty quantification for hyperbolic and kinetic equations, vol. 14 of SEMA SIMAI Springer Series, Springer, Cham, 2017. [4] L. LIU AND S. JIN, Hypocoercivity based sensitivity analysis and spectral convergence of the stochastic Galerkin approximation to collisional kinetic equations with multiple scales and random inputs, Multiscale Model. Simul., 16 (2018), pp. 1085–1114. [5] L. PARESCHI, An introduction to uncertainty quantification for kinetic equations and related problems, (2020). [6] B. SUDRET, Uncertainty propagation and sensitivity analysis in mechanical models–contributions to structural reliability and stochastic spectral methods, Habilitationà diriger des recherches, Université Blaise Pascal, Clermont-Ferrand, France, (2007). [7] C. VILLANI, Hypocoercivity, Mem. Amer. Math. Soc., (2009).
作者︰ 香港中文大学数学系助理教授刘鎏教授 2021年3月
