一种强大的数学建模工具---相场方法
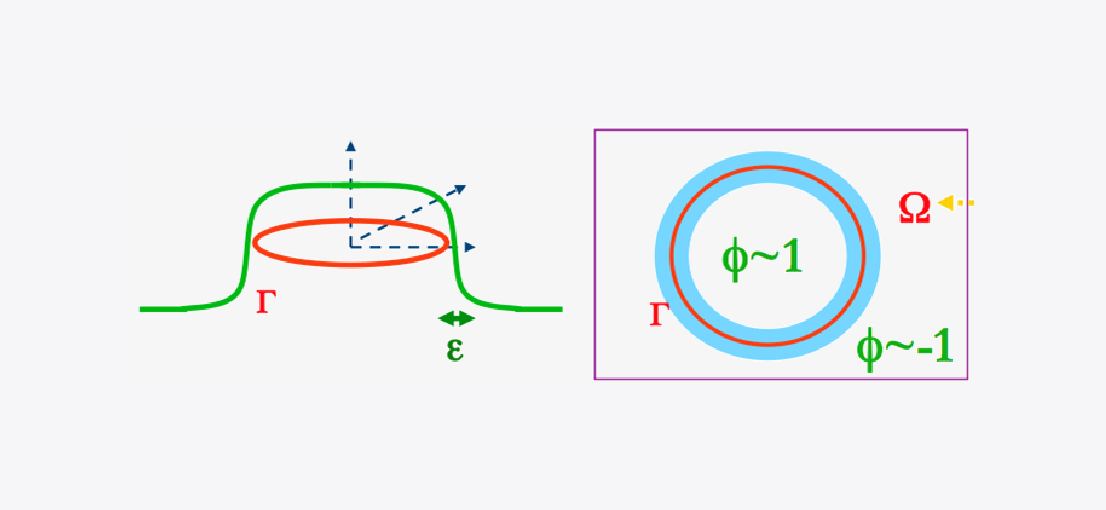
相场方法的思想来源可以追溯到Lord Rayleigh、Josiah Willard Gibbs 和 Van der Waals的研究。从那时起，它就成为了一种模拟和预测介观尺度形态和微观结构演变现象的强有力方法。这些现象在许多领域中都会产生，如生物学、材料科学、图像处理、多相流体力学、化学和石油工程等。科学家们设计出各种各样的相场模型，用于描述相分离和相变的过程。一般地，相场模型在每个相中取不同的数值（例如图1中的+1和-1），在接口周围有限宽度的薄层中，相值之间的变化是平滑的。
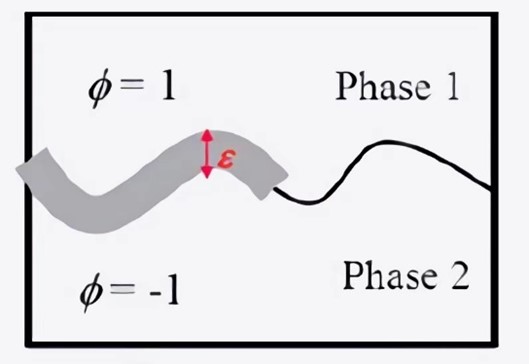
图1：相场函数
能量泛函在相场方法中起着至关重要的作用。在相场方法中，相分离与相变过程是能量驱动的，其动力学系统可以看作是某个Helmholtz能量泛函的梯度流。Helmholtz自由能泛函可以写为接口能量和相内自由能两部分能量之和。接口自由能是指储存在接口层的能量，可以通过相函数（图1中的 ϕ）来定义。正如预期的那样，它依赖于接口层的宽度（图1中的 ε）。另一方面，相内自由能通常是问题相关的，可能包括其他几种类型的能量，如动能和势能/梯度能。能量泛函的引入使得相场建模变得系统化。在实际应用中，相场建模的主要任务是建立Helmholtz自由能泛函和提供能量耗散机制的驱动力。
Allen-Cahn方程
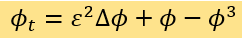(1)
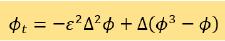(2)
是两个最著名的相场方程，它们分别是Helmholtz能量泛函
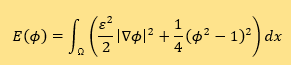(3)
的
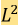和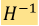 
梯度流，其中
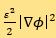为接口能密度， 
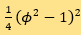是相内自由能密度，为一种常用的双阱势能。????是小的正参数，用来衡量扩散接口层的宽度。
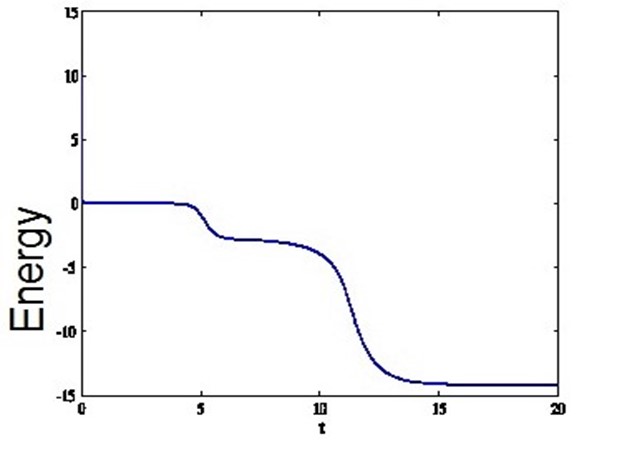
图2： 能量耗散
相场模型的高效数值方法
在得到相场模型后，如何高效地求解相场模型成为一个至关紧要的问题。在数值模拟中，为了设计出高效的数值方法，必须考虑如下几个重要的问题。首先，相场方程的一个固有性质是能量泛函随时间递减，即
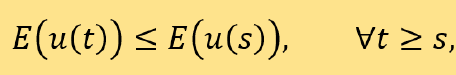
这通常被称为能量稳定性。为了在离散求解时保持梯度流结构，不仅要保证数值方法的准确性，还要保证离散格式的能量稳定性。这不是一个简单的任务，特别是在构建时间高阶离散格式的时候。在过去的十年中，人们发展了许多高效的能量稳定时间积分方法，并且把这些方法成功地应用于各种相场模拟之中。在离散求解时，保持与连续相场动力学相关的其他物理特征(如Allen-Cahn方程相场变量的逐点一致有界性)也得到了广泛的关注。对于相关数值分析方面的工作，读者可以参考[2, 7]及其参考文献。其次，为了刻画薄接口层，必须使用远小于接口层宽度ε的空间(和时间)网格尺寸来进行计算模拟（注意到ε远远小于1）。对于如此小的网格尺寸，会导致大规模的线性和非线性代数系统，求解这个代数系统需要耗费巨大的计算量。这一问题在空间均匀网格的三维情况中尤其突出。为了克服这一困难，可以采用空间自适应方法，只在接口层中使用细网格，而在远离接口层处使用较粗的网格。考虑到相函数有一个漂亮的结构轮廓，即在远离扩散界面的地方假设其为不同的值(接近常数)，而在扩散接口层有一个大的梯度，因此使用自我调整网格是一个自然的选择。最后，在相场方程的模拟中，通常需要较长的时间才能达到方程的稳态解，而在不同的时间阶段，Helmholtz能量泛函的递减速率可能会有很大不同。图2给出了Cahn-Hilliard方程一个数值模拟中的离散能量的耗散过程。一个很自然的想法是当能量递减速率快的时候使用较小的时间步长，否则使用较大的时间步长。文献[5]给出了一种自我调整方法，在实践中非常容易实现。自我调整时间步长由如下形式给出：
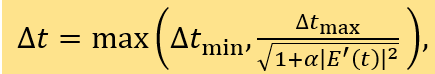
其中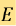
为相场模型中定义的Helmholtz能量泛函。????是用来调节自我调整程度常数。预先设定的最小时间步长 
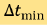强制给出自适应时间步长下界，避免时间步长过小。同样地，
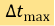给出了时间步长的上界。
应用
模拟相场模型的时间演化过程有着许多重要的应用，如相变、微观结构粗化和细胞运动等。根据Helmholtz自由能泛函的选择不同，各种各样的相场模型被构造出来，并用于模拟一些复杂的现象，如枝晶生长、合金凝固、多相流动、液晶和肿瘤生长等。其中，不少模型耦合了相场方程和其他物理模型，如Cahn-Hilliard-Navier-Stokes方程和Cahn-Hilliard微弹性模型。为了表征相分离和相变的不确定性，随机相场模型，如随机Allen-Cahn方程和随机Cahn-Hilliard方程，也成为了研究的热点问题。图3给出了在聚合物混合体系中大分子微球复合水凝胶在随机力效应下的结构演化模拟。最近几年，相场方法已成为图像分割(“湖中老虎”和“摄影师”的图像分割见图4)和高维数据分类的有效方法。文献[1]给了相关工作的一个综述，读者可以参考。
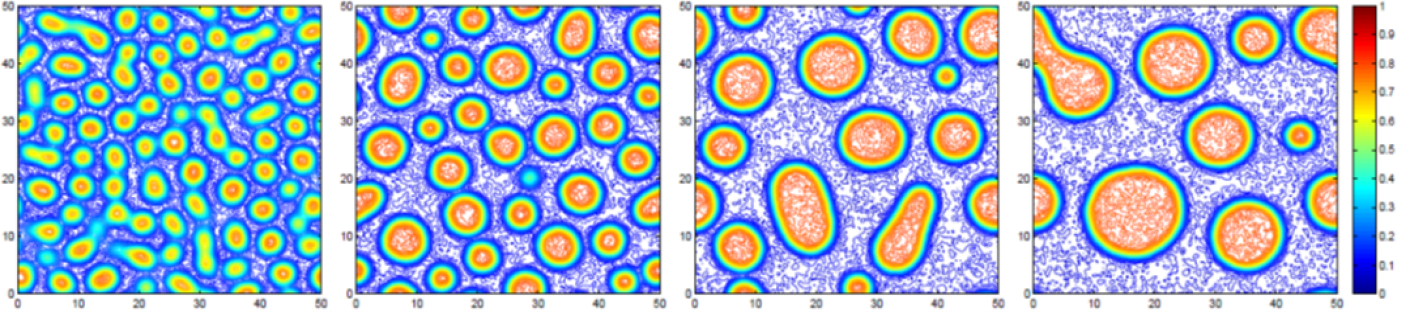
图3：大分子微球复合水凝胶[3]
图4：图像分割[4]
总结
相场方法是求解接口问题的一种有效的数学方法。在实际应用中，可以通过构造不同的Helmholtz自由能泛函来建立相应的相场模型。计算机模拟在对相场模型的研究中起着非常重要的作用。虽然发展稳定、高效的数值格式来求解相场模型已得到了人们持续关注，但是相场模型的数值模拟仍旧是具有挑战性的课题，特别是在高维问题模拟中，因为涉及的计算量非常巨大，困难变得尤其突出。事实上，极端尺度上的相场模拟已经被用来测试世界领先的高性能计算机的计算能力，如出现在Gordon Bell奖竞赛中的[5] (2011 Gordon Bell奖得主)和[8](2016年Gordon Bell奖入围，报告了迄今为止规模最大的3D相场模拟，在当时世界上最快的超级计算机上达到了每秒40千万亿次浮点运算，使用了超过3000亿个空间网格点，并利用了超过1000万个核)。随着相场建模在越来越多的应用领域得到推广和应用，对其发展和使用高效的数值算法和求解器，如自我调整网格方法，自我调整时间步长策略和并行计算技术，已成为迫切需要。
參考文獻
- Bertozzi A. L. and Flenner A. Diffuse interface models on graphs for classification of high dimensional data. SIAM Review, 2016, 58: 293-328.
- Du Q and Feng X. The phase field method for geometric moving interfaces and their numerical approximations, in Geometric Partial Differential Equations, Handbook of Numerical Analysis, 2020, 21: 425-508.
- Li X, Qiao Z and Zhang H. A second-order convex splitting scheme for a Cahn-Hilliard equation with variable interfacial parameters. J. Comput. Math., 2017, 35: 693-710.
- Liu C, Qiao Z and Zhang Q. Efficient numerical methods of the Allen-Cahn intensity fitting model for image segmentation. In preparation, 2020.
- Takashi S, Takayuki A, Tomohiro T, Akinori Y, Akira N, Toshio E, Naoya M, Satoshi M, and Malcolm C. Peta-scale phase-field simulation for dendritic solidification on the Tsubame 2.0 supercomputer. In Proceedings of 2011 International Conference for High Performance Computing, Networking, Storage and Analysis (SC ’11). Article No. 3, 2011.
- Tang T and Qiao Z. Efficient numerical methods for phase-field equations (in Chinese). Sci. Sin. Math., 2020, 50: 775-794.
- Qiao Z, Zhang Z and Tang T. An adaptive time-stepping strategy for the molecular beam epitaxy models. SIAM J Sci Comput., 2011, 33: 1395-1414.
- Zhang J, Zhou C, Wang Y, Ju L, Du Q, Chi X, Xu D, Chen D, Liu Y, and Liu Z. Extreme-scale phase field simulations of coarsening dynamics on the Sunway TaihuLight supercomputer. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, page 4. IEEE Press, 2016.
作者:
香港理工大学应用数学系教授乔中华教授
2020年1月