平均场博奕应用浅谈


平均场博奕（mean field game，MFG）理论专门探讨数量庞大的智能体（agent）在竞争环境下所使用的策略。每个智能体都会因应身边其他智能体所采取的行动而随之应变，务求令自可获得最大利益。例如，在股票市场，每位交易者为追求最高回报率，都会先留意其他交易者所采取的策略，再决定买入或卖出若干数量的股票。 「平均场」（mean field）一词本来是物理学术语，意思是大群体里的单一智能体行为对系统的影响微不足道。在典型的MFG里，智能体的行为是基于其他智能体的状态分布而作出反应，而非个别地针对其他智能体的行为而行动。例如，在购物市场里，某位客人可以在得知其他客人及卖家的交易资讯后才去购买商品，然而这种做法现实几乎不可能做到，而且费时失事。相反，在平均场的情境之下，他/她可以只看商品的价格就作决定，令决定的流程变得简单。在市场里，价格是由买卖双方经过互动而得出，因此，它蕴含了市场内所有智能体的状态及策略的概率分布。将价格视为平均场，能大大节省决策时间，而它本身亦可算是一种平均场。

MFG理论是由JM Lasry及PL Lions引入数学领域[1、2]，并由PE Caines、M Huang及RP Malhamé在工程界独立开发[3、4]。在有N人参与的博奕里，MFG就是当N趋向无限大时博奕的极限。在连续时间里，典型MFG的组成部分包括描述单一智能体之成本函数动态的Hamilton-Jacobi-Bellman方程式，以及描述所有智能体之聚合分布发展的Fokker-Planck方程式。到目前为止，MFG已派入多项用途，例如经济学[5、6]、社交网络[7、8]、机械学习 [9、10]等。

本文将探讨MFG的几种应用场合，包括机械学习、行人流量、流行病模型、婚姻领域。

1. MFG与机械学习

MFG与机械学习的交集可分为两个方向，第一是利用机械学习来有效率地解决高维的MFG，见[11、12、13]以及[14]对MFG数值方法的探讨。第二是运用MFG理论为机械学习提供解释及发展所需用到的见解[15]。本文将介绍MFG在聚类（cluster）分析及强化学习上的应用。

1.1 聚类分析

聚类分析是机械学习里一个经典问题。其中的难题是如何将一组数据点细分为子组，从而令同一组里的点彼此靠近，而非靠近其他组的点，见[20、21]。在[18、19]里，MFG模型被开发用于聚类分析，它们分别为K平均演算法[21]以及期望最大化演算法[22]的连续版本。

在[19]里，作者利用一个限定混合模型（概率密度函数的凸组合）来描述特定的数据集，视每个数据点为其中一个群体的一个智能体；每个群体则相当于混合模型的一个成分。每个群体的每个智能体均会依照自己的动态而移动，并尽量将一项无限时间成本泛函数降至最小；这项泛函数蕴含了智能体所在位置与群体重心（barycenter）之间的距离。作者在以上操作里得到的是一个多重群体MFG系统。 [19]里其中一项应用就是处理颜色量化的问题，其目的是将特定图像里的颜色总数减到固定数量K，从而令得出的图像尽可能与原来图像相似。图1为原来灰度图以及颜色分布。图2显示K=2、3、5个聚类时的结果，可见当聚类增加时，结果图像会越来越接近原图。


图1﹕黑白图像（a）及其灰度分布（b）（来源：[19]）

1.2 多智能体强化学习（multi-agent reinforcement learning，MARL）

现时，强化学习 (reinforcement learning，RL) 是深度学习里最热门的研究范畴之一。 AlphaGo以及许多著名的强化学习应用个案，大体上均是以单一智能体或少数智能体的群体为基础。当中的智能体会因应环境而作决定并获得回报；而MARL则出现在更复杂的情境，例如，在交通网络里，司机的行为会受到环境及周围其他司机的影响，因此，在交通车流里要顾及大量智能体的行为。最近，MARL在某些应用场合里已运用成功。


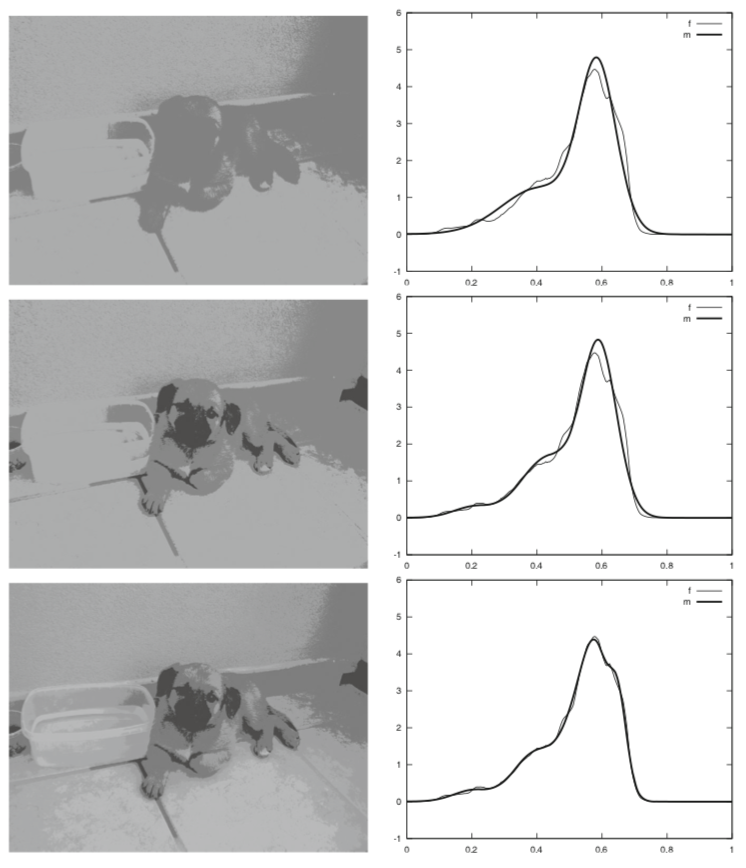
图2﹕当K = 2、3、5（由上至下）时，透过MFG聚类（左）及相应的混合（右）进行颜色量化（来源：[19]）

例如，OpenAI建立了一个可以攻破Dota2的系统，而DeepMind亦在Quake III游戏里破关。一般而言，由于直接打破纳殊均衡点（Nash equalibrium）需要复杂的计算，因此当智能体数量增加时，MARL在处理上会更加吃力，此时MFG正好可用来简化包含大量智能体的复杂MARL情境。在MFG里，每个智能体不会逐一回应其他智能体的动作，而是因应其他智能体的分布而行动；分布图集合了其他智能体的动作及状态

在[16、17]里，作者提出结合MFG及MARL里的不同技巧。 [16、17]其中一项实验的主题是合作-竞争交战混合博奕，当中，两方军队要在划分成网格的世界里对抗；每边军队由不同的RL演算法驱动。在图3a的设置下，每支军队包含64个同质智能体。每支军队可以与队友合作摧毁所有成分，从而获得更多回报。在示例中，演算法、Q-learning（QL）及有利演员(advantageous actor，AC)均依照其各自的平均场对应物、平均场Q-learning (MF-Q)及平均场有利演员(MF- AC)接受了测试。作者安排了二千轮自我对弈来训练四个模型。训练期间，智能体迅速掌握了追击及合作的击杀对手技能。图4为二千轮交叉比较实验的胜率及总回报结果。我们见到MF-Q大体上比其他演算法出色，显示平均场MARL演算法有其效用。

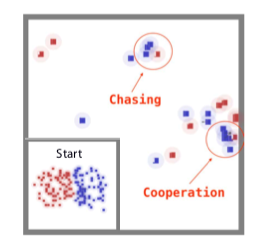
(a) 交战博奕场景

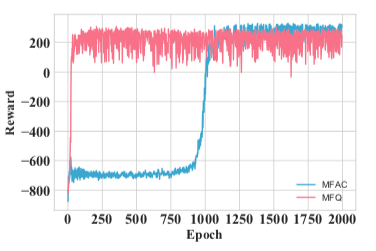
(b) 学习曲线

图3﹕交战博奕﹕64比64（来源:[16]）


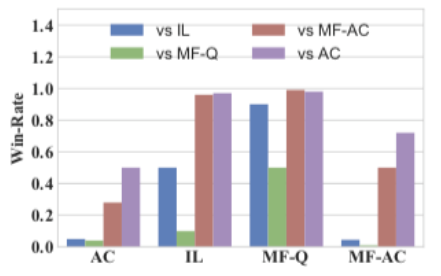
(a) 平均胜率

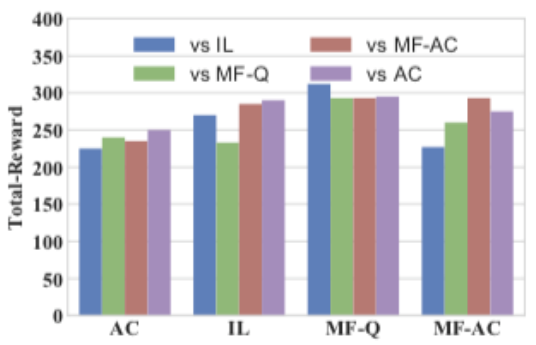
(b) 平均总回报

图4﹕交战博奕表现比较（来源﹕[16]）。

MFG在学习上尚有其他有意思的应用，本文无法一一列举。例如，[24]提出了一套通用的MFG框架，可同时执行学习及决策，并就重复广告竞价问题进行实验。 MFG与机械学习两者相结合目前仍然只处于纯綷理论的层面，业界并未广泛应用，然而在初试啼声之后，所展示出的潜力令人难以置信。 MFG可以为学习任务订立严格的框架，又能利用无限个智能体将大规模的系统简化。

2. 行人流

行人的流动是由大量智能体的决定所组成。我们通常都要考虑人流里的拥塞效应，当中每一个智能体的成本取决于众多智能体的移动速度非线性组合，以及整个群体的分布，因此，以在非常挤塞的区域为例，智能体情愿以慢速移动。 PL Lions于2011年在[25]里引入并研究带有拥塞效应的MFG，另见[14、26、27、28]的几项数值模拟。

本文会介绍[14、28]的示例。在[14，28]里，作者模拟的处境是行人被赶离设有数个长方形障碍物的特定正方形大堂，如图5所示。


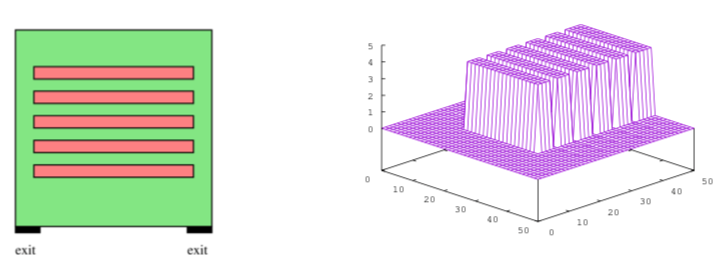
图5﹕左﹕平面图（障碍物为红色）；右﹕密度（当t=0）（来源:[14]）

图5里，大堂有红色障碍物；底下有两个出口。我们想像封闭的建筑物发生恐慌时，行人争相走向出口；红色的障碍物是坐椅。当t=0时，所有人都坐在椅上，如图5右所示。图6显示t=1、5、15分钟时，人群的概率密度。我们见到行人冲向最靠近自己的大堂两侧窄走廊，然后跑向出口，我们又留意到，走廊交汇处的人群密度为最高。在研究[14、28]里，作者亦留意到拥塞效应，即在密度高的区域速度会变低。


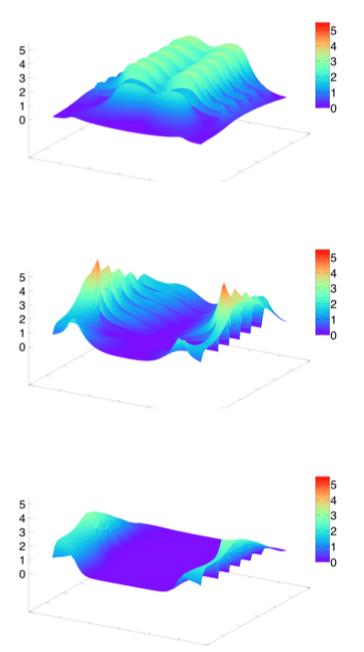
图6﹕两个模型在不同日期所计算到的密度，t=1、5、15分钟（由上至下）（来源:[14]）

3. 流行病模型

2019冠状病毒病（COVID-19）大流行至今仍然肆虐，影响全球每个角落，关于COVID-19模型的研究论文的大量出版。对于涉及庞大群众行动的流行病，MFG理论是有效的研究工具；已有几篇论文为COVID-19提供多个MFG模型，见[29、30、31]。在[29]里，作者提出一个能够控制流行病在空间域（spatial domain）上传播的平均场控制模型。 [29]的模型是建基于已为人熟知的SIR模型[32]；S、I、R分别代表健康（susceptible）、感染（infected）、康复（recovered）的人数。这个经典的SIR模型只包含与随时间变化有关的普通微分系统。由于诸如COVID-19的严重流行病会在全球各地传播，因此在量度疾病的传播以及人员的感染及移动时必须考虑空间类型的SIR模型。在[29]里，作者在建立病毒在空间域里的传播时，结合了源自SIR模型及MFG模型的构思。这个模型的目标，是将受感染的智能体数量以及群体的移动量降至最低。

[29]其中一项实验是研究不同康复率的影响。


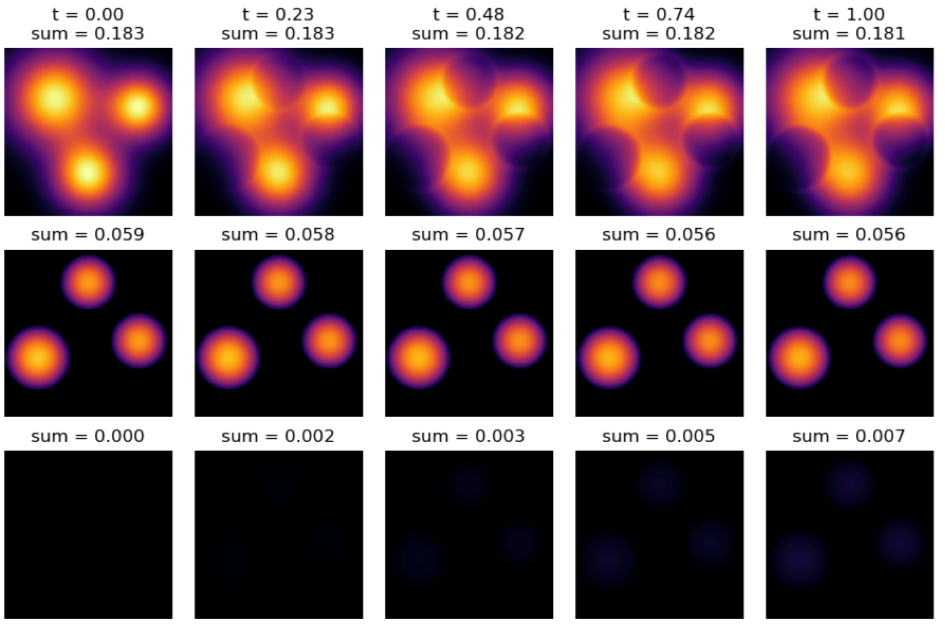
图7﹕低康复率时，各个群体于不同时间的变化。第一行代表健康，第二行代表感染，最后一行代表康复。 （来源:[29]）

图7显示低康复率时t=0至t=1各个群体的概率密度。图7里第一行是健康者的变化，第二行是感染者的移动，最后一行是康复群体的变化。随着时间发展，我们会看到健康群体与感染人群分开；由此可以推断，当康复率较低时，最佳策略是防止健康群体受感染。

图8显示高康复率时各个群体的变化，代表疫苗推出市面时的情况。由图8可见，随着时间发展，健康群体并无太大变动；受感染的人变少，康复的人渐多。实验显示，当康复率较高时，减少感染人数的最佳策略是专注于令感染者康复，而非调动健康群体。


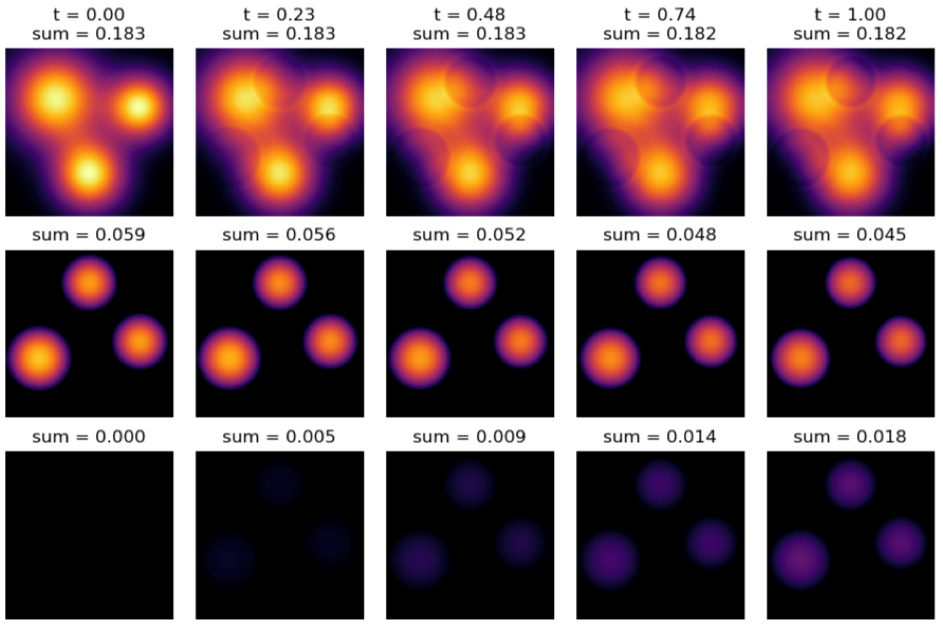
图8﹕高康复率时，各个群体于不同时间的变化。第一行代表健康，第二行代表感染，最后一行代表康复。 （来源:[29]）

4. MFG在婚姻的应用

在以下最后的一个例子，我们会介绍MFG在婚姻上的有趣应用。在[33]里，作者使用了随机微分方程式来模拟夫妻的感情状态。影响感情状态的因素有随机事件、父母、子女、朋友，以及婚姻状况的社会分布。数学模型可帮助我们更加了解感情的动态变化，并为夫妻提出合适的干预或治疗方案。 [33]之前的研究均无考虑无法预测因素、噪讯、随机事件，以及感情状况的社会分布，而平均场模型正是此类问题的理想模型，因为社会、朋友、夫妻的父母可能会联合影响他们。 [33]模型的平均场描述了在社会里夫妻感情状况的分布。

在[33]里，多位作者所考虑的是一套平均场感情博奕，他们一致认为，朋友、父母、朋友的朋友、社会环境里的感情状况均会对夫妻有影响。例如，当某对夫妻有很多朋友均处于较低的感情状况时，离婚机会就会提高。另外，夫妻感情状况亦会传播并影响朋友的朋友，以至更远，因此，作者将社会里的社会性质影响及外部影响引入婚姻博奕。

从数字结果而言，[33]的研究显示，如果努力的成本并非太高而且最初感情状况并非太低，夫妻努力修复婚姻仍可能有助于维持婚姻。研究又显示，自己认识太多已离婚的人，可能会适得其反，对婚姻状况带来不良影响，即是认识离婚的人越多，自己婚姻就越大可能破裂。然而这样并不表示，某对夫妻会因为他们的朋友婚姻正在破裂而离婚。婚姻状况亦取决于夫妻的努力及社会环境。这项研究有助我们从理论上明白与婚姻相关的过程，从而有助我们设计或评估对婚姻的介入措施。

上述的应用层面还远远未达完成阶段。而从以上的例子我们亦可以见到，当要处理涉及大量智能体的系统时，MFG理论是有效率的模型建立工具。如今「大数据」大行其道，相信MFG与其他领域交集的机会将越来越多。

参考文献


  1. J. M. Lasry and P. L. Lions, Jeux à champ moyen. I. Le cas stationnaire. C. R. Math. Acad. Sci. Paris, 343(9):619–625, 2006.
  2. J. M. Lasry and P. L. Lions, Jeux à champ moyen. II. Horizon fini et contrôle optimal. C. R. Math. Acad. Sci. Paris, 343(10):679–684, 2006.
  3. M. Huang, P. E. Caines, and R. P. Malhamé. Large-population cost-coupled LQG problems with nonuniform agents: individual-mass behavior and decentralized ϵ-Nash equilibria. IEEE Trans. Automat. Control, 52(9):1560–1571, 2007.
  4. M. Huang, R. P. Malhamé, and P. E. Caines. Large population stochastic dynamic games: closed-loop McKean-Vlasov systems and the Nash certainty equivalence principle. Commun. Inf. Syst., 6(3):221–251, 2006.
  5. Y. Achdou, J. Han, J. M. Lasry, P. L. Lions, and B. Moll. Income and wealth distribution in macroeconomics: A continuous-time approach. Technical report, National Bureau of Economic Research, 2017.
  6. G. Olivier, J. M. Lasry, and P. L. Lions. Mean field games and applications. In Paris-Princeton lectures on mathematical finance 2010, pp. 205-266. Springer, Berlin, Heidelberg, 2011.
  7. B. Dario, H. Tembine, and T. Basar. Opinion dynamics in social networks through mean-field games. SIAM Journal on Control and Optimization 54, no. 6 (2016).
  8. L. Jian, B. Xia, X. Geng, H. Ming, S. Shakkottai, V. Subramanian, and L. Xie. Mean field games in nudge systems for societal networks. ACM Transactions on Modeling and Performance Evaluation of Computing Systems (TOMPECS) 3, no. 4, 2018.
  9. C. Haoyang, X. Guo, and M. Laurière. Connecting GANs, MFGs, and OT. arXiv e-prints (2020): arXiv-2002.
  10. S. Jayakumar, and A. Mahajan. Reinforcement learning in stationary mean-field games. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems, pp. 251-259. 2019.
  11. C. René, and M. Laurière. Convergence Analysis of Machine Learning Algorithms for the Numerical Solution of Mean Field Control and Games: II--The Finite Horizon Case. arXiv preprint arXiv:1908.01613 (2019).
  12. C. René, and M. Laurière. Convergence Analysis of Machine Learning Algorithms for the Numerical Solution of Mean Field Control and Games: II--The Finite Horizon Case. arXiv preprint arXiv:1908.01613 (2019).
  13. R. Lars, S. J. Osher, W. Li, L. Nurbekyan, and S. W. Fung. A machine learning framework for solving high-dimensional mean field game and mean field control problems. Proceedings of the National Academy of Sciences 117, no. 17, 2020.
  14. A. Yves, and M. Laurière. Mean field games and applications: Numerical aspects. arXiv preprint arXiv:2003.04444, 2020.
  15. W. E, J. Han, and Q. Li. A mean-field optimal control formulation of deep learning. Research in the Mathematical Sciences 6, no. 1 (2019): 1-41.
  16. Y. Yang, R. Luo, M. Li, M. Zhou, W. Zhang, and J. Wang. Mean field multi-agent reinforcement learning. In International Conference on Machine Learning, pp. 5571-5580. PMLR, 2018.
  17. M. David, J. Jennings, S. V. Macua, E. Sison, S. Ceppi, and E. M. D. Cote. Coordinating the crowd: Inducing desirable equilibria in non-cooperative systems. arXiv preprint arXiv:1901.10923, 2019.
  18. J. L. Coron. Quelques exemples de jeux à champ moyen, Ph.D. thesis, Universite Paris-Dauphiné, 2018.
  19. A. Laura, S. Cacace, F. Camilli, and R. D. Maio. A mean field games approach to cluster analysis. Applied Mathematics & Optimization (2020): 1-25.
  20. B. Christopher M. Pattern recognition and machine learning. springer, 2006.
  21. S. Amit, M. Prasad, A. Gupta, N. Bharill, O. P. Patel, A. Tiwari, M. J. Er, W. Ding, and C. Lin. A review of clustering techniques and developments. Neurocomputing 267 (2017): 664-681.
  22. B. Leon, and Y. Bengio. Convergence properties of the k-means algorithms. In Advances in neural information processing systems, pp. 585-592. 1995.
  23. J. A. Bilmes. A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models. International Computer Science Institute 4, no. 510 (1998): 126.
  24. X. Guo, A. Hu, R. Xu, and J. Zhang. Learning mean-field games. arXiv preprint arXiv:1901.09585 (2019).
  25. P. L. Lions, Cours du Collège de France, http://www.College-de-france.fr/default/EN/all/equ−der/, 2007-2011.
  26. Y. Achdou. Finite difference methods for mean field games. In Hamilton-Jacobi equations: approximations, numerical analysis and applications, pp. 1-47. Springer, Berlin, Heidelberg, 2013.
  27. Y. Achdou, and J. M. Lasry. Mean field games for modeling crowd motion. In Contributions to partial differential equations and applications, pp. 17-42. Springer, Cham, 2019.
  28. Y. Achdou, and M. Lauriere. On the system of partial differential equations arising in mean field type control. arXiv preprint arXiv:1503.05044 (2015).
  29. W. Lee, S. Liu, H. Tembine, W. Li, and S. Osher. Controlling Propagation of epidemics via mean-field control. SIAM Journal on Applied Mathematics 81, no. 1 (2021): 190-207.
  30. S. Cho. Mean-field game analysis of SIR model with social distancing. arXiv preprint arXiv:2005.06758 (2020).
  31. A. Alexander, R. Carmona, G. Dayanikli, and M. Lauriere. Optimal incentives to mitigate epidemics: a Stackelberg mean field game approach. arXiv preprint arXiv:2011.03105 (2020).
  32. W. O. Kermack, and M. G. Anderson G. A contribution to the mathematical theory of epidemics. Proceedings of the royal society of london. Series A, Containing papers of a mathematical and physical character115, no. 772 (1927): 700-721.
  33. B. Dario, B. M. Dia, B. Djehiche, H. Tembine, and R. Tempone. Mean-field games for marriage. PloS one 9, no. 5 (2014): e94933.

作者：
香港城市大学数学系助理教授牟宸辰博士

2021年7月