Background of research:
Kinetic equations are widely used in many important areas such as rarefied gas, plasma physics, astrophysics, and have also seen a host of new applications such as semiconductor device modeling, environmental, social and biological sciences. They describe the non-equilibrium dynamics of a gas system composed of a large number of particles. The solutions to kinetic models determine the probability density functions of the dynamical states of a large number of particles, which usually depend on time, space and velocity. Kinetic equations bridge atomistic and continuum models in the hierarchy of multiscale modeling. The diagram below shows where kinetic equations stand in the hierarchy of different physics models from microscopic to macroscopic:
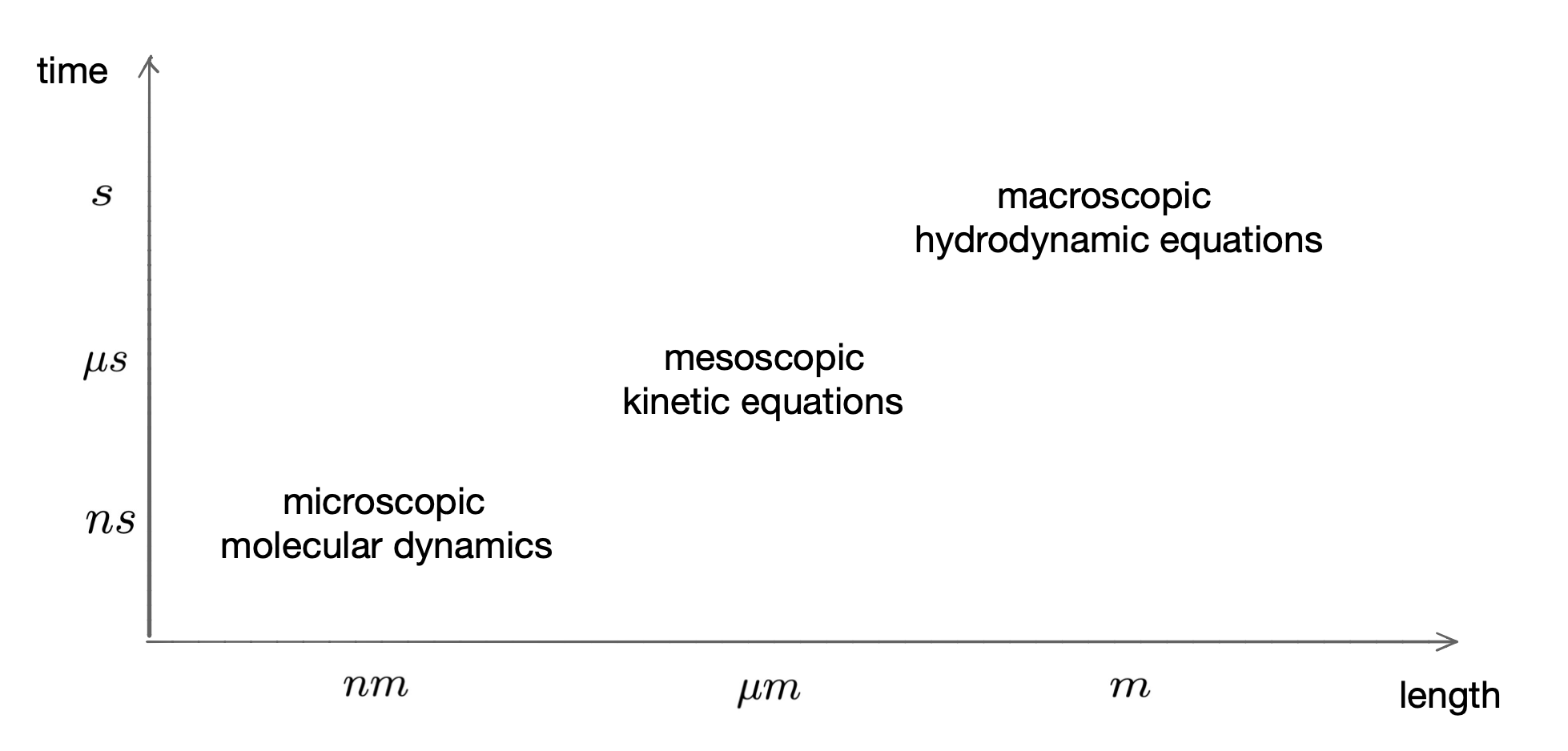
Fig 1: Physics models of different scales. (CAR).
The Boltzmann equation, founded by Ludwig Boltzmann in 1872, is one of the most important examples of kinetic models. It is an integro-differential equation that describes particle transport and binary collisions of a rarefied mono-atomic gas. In the past decades, there have been enormous studies on the Boltzmann equation, both in theory and numerical computation. Its dimensionless form reads 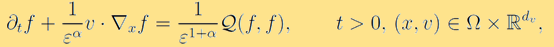 where
where 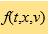 is the probability density distribution function that models the probability of finding a particle at time t, at position
is the probability density distribution function that models the probability of finding a particle at time t, at position 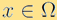 , and with velocity
, and with velocity  . The Knudsen number
. The Knudsen number 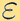 is the dimensionless mean free path, characterises the degree of rarefiedness of the gas. The constant
is the dimensionless mean free path, characterises the degree of rarefiedness of the gas. The constant  refers to different scalings. The operator
refers to different scalings. The operator  models the binary collisional interactions between particles and is given by
models the binary collisional interactions between particles and is given by
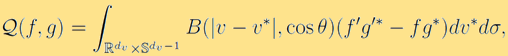 where
where 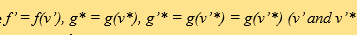 are the post-collisional velociies) and
are the post-collisional velociies) and 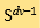 is the
is the 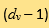 dimensional unit sphere. The collision kernel
dimensional unit sphere. The collision kernel  is a non-negative function that describes the transition rate during particle collisions.
is a non-negative function that describes the transition rate during particle collisions.
As for applications of kinetic models, for example, aerospace activities arise in many problems of rarefied gas dynamics. A rich harvest of research activities was achieved in the last fifties and sixties thanks to the spectacular space programs, which led to numerous theoretical and experimental problems concerning flows of neutral and ionised gases. See [1] for an overview of developments of the Boltzmann equation and rarefied gas dynamics in the last decades. One of the most significant applications are flows over reentering vehicles, in particular kinetic heating, drag and energy balance of satellites, the exhaust volume of rockets operating at extreme altitudes and in space, design high-atmosphere sounding devices, production of gas clouds at extreme altitudes, etc. The Boltzmann equation also has extensive and important applications in other fields, such as astrophysics, plasma physics, design of particle accelerators or semiconductor devices and so on.

Several challenges:
Kinetic equations, usually derived from N-body Newton’s equations via the mean field limit, typically contain an integral operator modeling interaction between particles. Calculating the collision kernel from first principles is not possible for complex systems, thus only empirical formulas are used in practice. Other sources of uncertainties may come from inaccurate measurements for the initial or boundary data, forcing or source terms etc. These uncertainties contribute to the curse of dimensionality and bring challenges to the development of efficient numerical methods.
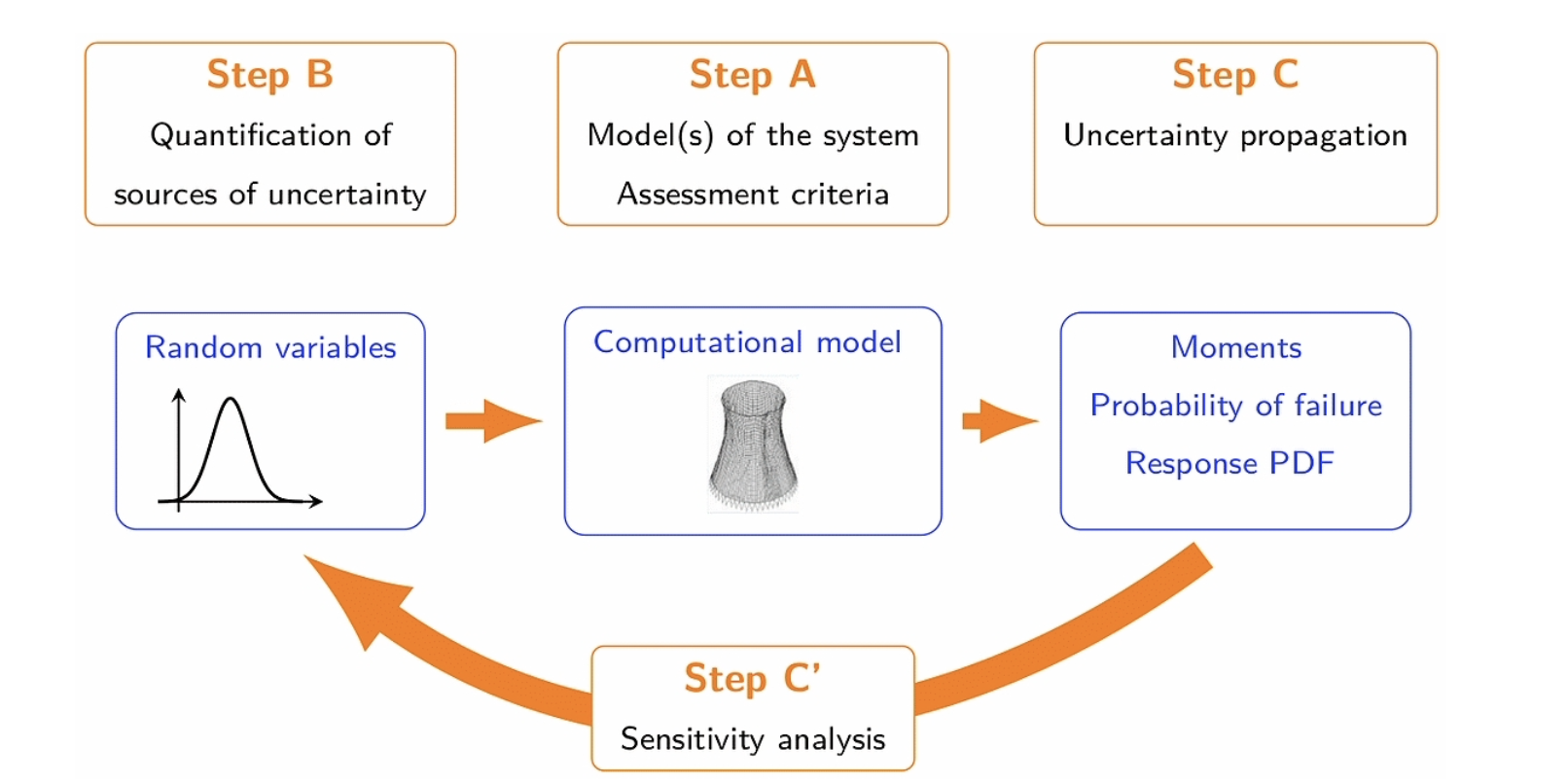
Fig 2: General scheme for posing uncertainty quantification problems. Fig from [6].
Uncertainty Quantification (UQ), on the other hand, is a hot topic that has drawn considerable attentions in applied mathematics over the past decade. Quantifying uncertainties in the inputs of models is important to assess, validate and improve the underlying models, allowing us to obtain more reliable predictions for the outputs and better risk assessment. The figure below provides a general scheme that is used to identify the key ingredients of general UQ problems:
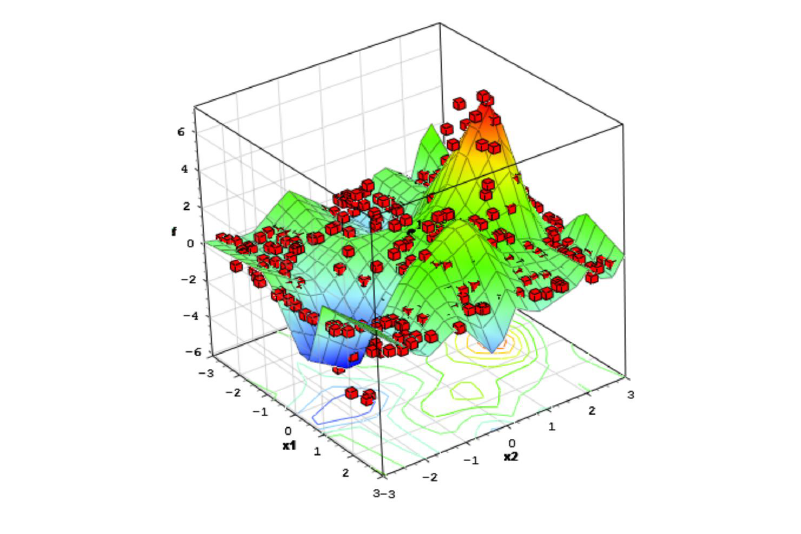
Fig 3: Challenge for high-dimensional UQ problems: high computational cost.
Another main computational challenge for kinetic problems is that these models often encounter multiple temporal and spatial scales, characterised by the Knudsen number 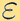 that may vary dramatically in orders of magnitude in the computational domain, covering from fluid, transition to rarefied regimes. One effective computational paradigm is Asymptotic-Preserving (AP) schemes [2], which has been very popular in kinetic and hyperbolic communities in the last two decades. We show an illustration of the idea below. An AP scheme preserves the discrete analogy of the asymptotic passage from a microscopic model to its macroscopic model, without numerically resolving the small Knudsen number thus can reduce the computational cost significantly.
that may vary dramatically in orders of magnitude in the computational domain, covering from fluid, transition to rarefied regimes. One effective computational paradigm is Asymptotic-Preserving (AP) schemes [2], which has been very popular in kinetic and hyperbolic communities in the last two decades. We show an illustration of the idea below. An AP scheme preserves the discrete analogy of the asymptotic passage from a microscopic model to its macroscopic model, without numerically resolving the small Knudsen number thus can reduce the computational cost significantly.
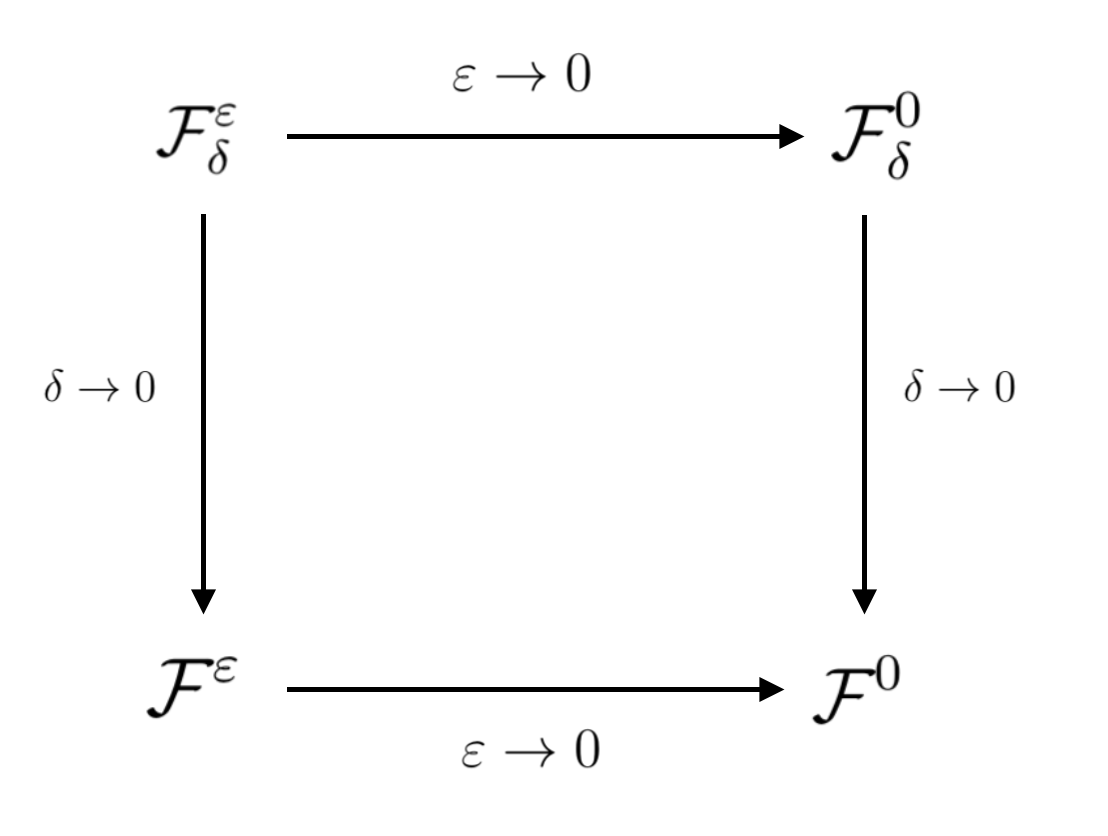
Fig 4: A diagram of an AP scheme [2].
Some results:
1. Analysis
Hypocoercivity theory is a useful and important tool to study the stability and long-time behaviour of the solution for kinetic equations. According to [7], the study for the dissipative evolution equation such as (1) involves (i) a degenerate dissipative operator, and (ii) a conservative streaming operator 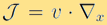 such that the combination of both operators implies convergence to a uniquely determined equilibrium state. The key for the analysis is to construct a new Lyapunov functional, which is equivalent to the Sobolev norm and can be shown to decay to zero exponentially in time.
such that the combination of both operators implies convergence to a uniquely determined equilibrium state. The key for the analysis is to construct a new Lyapunov functional, which is equivalent to the Sobolev norm and can be shown to decay to zero exponentially in time.
The local sensitivity analysis allows one to determine how sensitive the solution depends on the random uncertainties in the model. By extending the hypocoercivity theory developed for general collisional linear and nonlinear kinetic equations for deterministic problems to the random uncertain setting, in [4] we established the regularity and long-time behaviour of the solution with random initial data and random collision kernel in particular for the Boltzmann equation, under suitable assumptions. The framework provided is quite general, ranging from the Boltzmann and Landau equations, to the semi-classical relaxation type quantum Boltzmann equation and linear transport equations. There are a series of work in this direction [3].
2. Numerical methods
We are interested in developing efficient numerical methods for multiscale kinetic problems with uncertainties, and have made several contributions on this topic. In general, we mention some of the main methods reviewed in [5]:
In the past few years, we have achieved significant results on both analysis and numerical methods for solving multiscale kinetic equations with uncertainties. In the future, we desire to explore further on this topic and extend its applications to broader research areas.
References:
[1] C. CERCIGNANI, The Boltzmann equation in the whole space, in The Boltzmann Equation and Its Applications, Springer, 1988, pp. 40–103. [2] S. JIN, Efficient asymptotic-preserving (AP) schemes for some multiscale kinetic equations, SIAM Journal on Scientific Computing, 21 (1999), pp. 441–454. [3] S. JIN AND L. PARESCHI, eds., Uncertainty quantification for hyperbolic and kinetic equations, vol. 14 of SEMA SIMAI Springer Series, Springer, Cham, 2017. [4] L. LIU AND S. JIN, Hypocoercivity based sensitivity analysis and spectral convergence of the stochastic Galerkin approximation to collisional kinetic equations with multiple scales and random inputs, Multiscale Model. Simul., 16 (2018), pp. 1085–1114. [5] L. PARESCHI, An introduction to uncertainty quantification for kinetic equations and related problems, (2020). [6] B. SUDRET, Uncertainty propagation and sensitivity analysis in mechanical models–contributions to structural reliability and stochastic spectral methods, Habilitationà diriger des recherches, Université Blaise Pascal, Clermont-Ferrand, France, (2007). [7] C. VILLANI, Hypocoercivity, Mem. Amer. Math. Soc., (2009).
Author: Prof Liu LIU Assistant Professor, Department of Mathematics The Chinese University of Hong Kong March 2021
