我们在“大众与科学”中曾介绍国际数学建模挑战赛(IM2C)。这是一项面向全球中学生的国际性新型数学建模竞赛。在中华国际数学建模挑战赛委员会和参赛学校的协助下,我们很高兴与大家分享2020年度中华区赛事的其中一个赛题(智能水务数据分析)和得奖论文。
水是人们日常生活中不可或缺的一部分,为了用户的利益,我们需要一个高效能的水力运输系统。然而在供水系统中,一些系统故障的情况,如水管或阀门故障,很容易导致漏水问题。因此,工程师和研究人员正不断寻找各种方法去建构智能水务系统令供水更为有效。所以,电磁流量计多用于量度水流和检查漏水情况。如详细分析一个地区里的水输入和输出量的差异,从而清楚反映水流状态和潜在的漏水风险。尽管当今有许多数据分析方法可供使用,但一些挑战仍然存在。国际数学建模挑战赛(IM2C)便将此挑战为基础为中华区中学生设立赛题。
为秉持所有IM2C的赛题均来自现实世界之特色,香港应用科技研究院(ASTRI)专家从他们的实际研发项目来创设此赛题。赛题原文及包含 8 个不同虚拟区域中输入和输出水流量之差的数据集可见于此。
香港的拔萃女书院团队以此问题的建模方案论文荣获2020年度IM2C中华区特等奖,本文由作者从获奖报告缩写而成。
如果您是中学生或于中学任教并有兴趣参与这项挑战,请留意IM2C网站的最新资讯。
学生:林慧心, 苏泳潼, 黄嘉愈, 余瑞琦
指导教师:杨宝琪
我们先分析数据模式,并指出鉴定异常水流的准则。我们发现在已给8个地区的数据波动普遍很大,没有明显的规律。但水输入和输出量的差异(简称实际数值)徘徊于-12和24之间。我们断定细小的水流波动由人们每天用水量的细微转变导致,而较大的水流波动则因异常水流而致。
在已给8个地区的水输入和输出量差异中,我们根据其相对数据集计算8个模型函数。藉此可预测各地区的水流趋势,从而检测异常水流和漏水情况。R2数值测量了模型函数的准确度。如果R2 > 0.5,该模型函数会被视为一个好模型(正如很多科学家所指)。数值越近 1,模型函数便越准确。由于这 8 个地区的R2数值都小于 0.5,可见这些数据都极为分散,且没有直接关系。
识别异常的第一个标准是考虑每天的实际值,这方法可以于短时间内发现问题,如实值超出正常范围的5%,则被列为异常,并将此现象归类为严重漏水问题。
第二个标准是总出水量突然变化。通过计算 5 个连续点的平均斜率,我们可找到变化的幅度。如果斜率超过正常斜率范围的5%,则为异常。这可帮助我们发现较小的漏水问题,因为那个点可能并未超出正常范围,但它显示出恶化的趋势,所以如果不加注意,它可能会变成更严重的漏水问题。
然后我们根据数据分析结果,开发一个通用的数学模型对 8 个虚拟区域进行异常值检测。
第一个方法是找出实际数值的正常范围。
我们先找出数据中心简单移动平均数。我们设第x天的实际数值为Ax。由于用来计算首7天和最后7天(第1-7, 94–100天)的中心简单移动平均值的数据不足以计算15天的中位数,因此这些日子需另作计算。否则计算第x天的移动平均值便会通过此公式计算:( Ax-7 + Ax-6 + ... + Ax + Ax+6 + Ax+7 ) / 15 . 首7天的中心简单移动平均值的公式是 ( A1 + A2 + A3 + ... + A2x-1 ) / ( 2x -1 ) ; 最后7天的中心简单移动平均值的公式是 ( A2x-100 + ... + A98 + A99 + A100 ) / ( 201 - 2x ) .
然后我们使用以下公式计算移动方差:
移动方差 = (实际值(x) - 实际值的平均值)2的移动平均值
计算移动标准偏差值的公式:
移动标准偏差 = 移动方差的平方根
上限 = 实际值的移动平均值 + 2 x 移动标准偏差值
下限 = 实际值的移动平均值 - 2 x 移动标准偏差值
下图为其中已给地区7的正常值域数据:
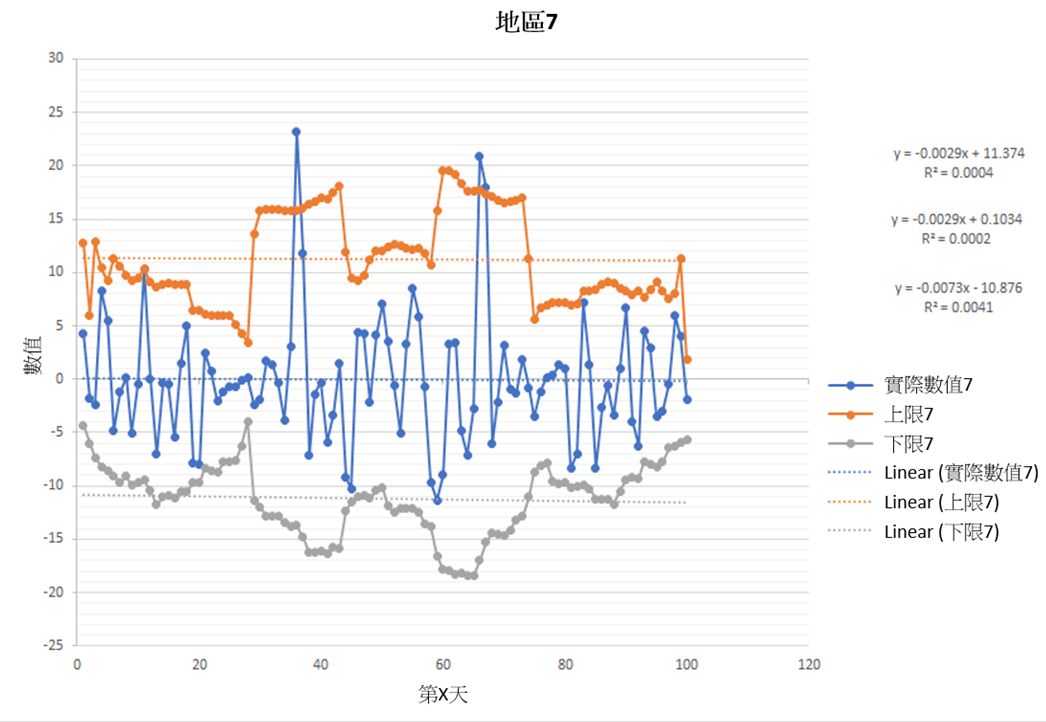
移动标准偏差值会被乘以2因为它包含约95% 数据,这意味着约5% 数据不在正常值域里,它们被认定为异常。由于不同区域有不同的移动平均线,因此每个区域的移动标准偏差根据相应的数据和水流情况方面是不同的,必须单独计算。
移动平均值允许我们分析数据的趋势,而不是分析个别数据。这是因为我们需要比较不同的数据来确定水流是否异常,并且还可以让我们预测水流的趋势。我们还使用了较长的移动平均值(每个间隔15天),这可以消除短期的水流波动并突出长远的趋势从而简化计算。此外,使用奇数的间隔有助简化检查过程。我们只需要在数据中找一个数字,看看它是否与计算出的平均值相差很大即可,有助于减少发生异常的可能性。
计算移动平均值可以用简单移动平均法和累积移动平均法计算,但我们只使用了简单移动平均法。这是因为它只参考最近期的数据,并且可以更迅速地发现异常现象。相反,累积移动平均值参考的数据是由第一天开始计算。第x天 (CMAx) 的累积移动平均值的计算算式是 ( A1 + A2 + ... + Ax ) / x , 第x天的实际值以 Ax代表。第x + 1天的累积移动平均值的计算算式即是 ( Ax+1 + x(CMAx)) / ( x+1 ) 。如果数据集中有异常数据,我们未必能迅速发现,这是因为在这个方法中,有大量的数据被列入考虑。因此,即使我们发现了有异常数据,它也未必完全可信,因为这可能被其他先前多个异常数据累积而影响。而且,由于日子的数量是双数,即 100,我们不可能找到一个整数中间数。因此,我们选择了用中心简单移动平均法,此方法会于已计算的移动平均值再取之平均值,则能使已计算的移动平均值更平滑和从中找出一个中间数。
我们的第二种方法是计算数据的正常斜率值域。
图表上的每个斜率都代表着一定天数内水输入和输出量之间的差异的变化。因水输入量维持一样,所以当图表上的一个数值异于前一个时,可见出水量就会发生变化。因此,我们可以使用斜率来衡量出水量增加或减少的幅度。如上所述,用简单标准偏差计算,当5个连续点的平均斜率在该区的实际值模型函数之上,即大于数据正常范围,就被认为是一个总出水量大幅减小的情况,反之亦然。
我们选择了5个连续数据进行计算,因为如果我们考虑太少数据,就不能准确认定水流是否由于其他因素(如电磁流量计的故障),而出现异常情况。同时,若考虑太多数据,将降低发现异常漏水问题的效率,从而无法在漏水问题变得严重前发送警告信号。因此,我们考虑了5个数据。
为了计算数据的正常斜率范围,我们首先找出每5个连续数据之间的平均斜率,然后计算它们的平均值。然后,我们使用以下公式计算值的方差:
方差 = (实际值 - 实际值的平均值)2的平均值
接着,我们通过计算出方差的平方根来计算简单标准偏差。
然后使用以下公式计算斜率范围:
正常斜率范围的上限 = 实际斜率平均值 + 2 x 简单标准偏差
正常斜率范围的下限 = 实际斜率平均值 - 2 x 简单标准偏差
就如移动标准偏差,简单标准偏差必须乘以2,才能覆盖正常数据的95%。因此剩余的5% 被视为异常。
下图为已给地区7的正常斜率值域数据:
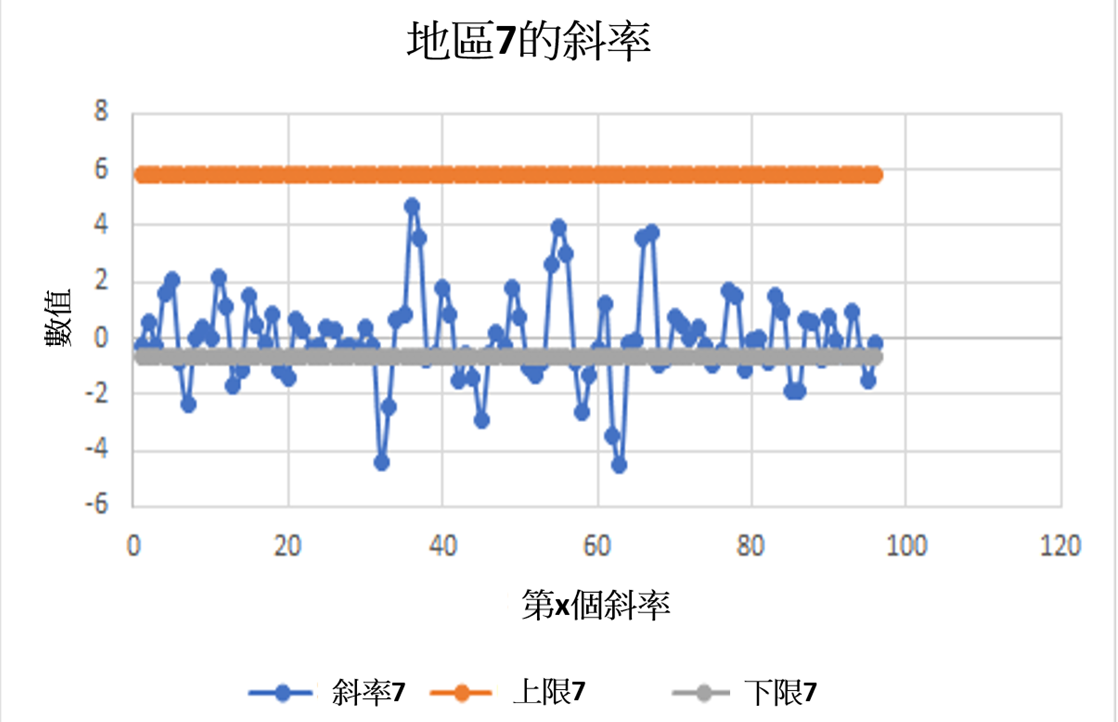
设计完数学模型后,我们对两种方法进行了比较。使用数据正常范围的方法运用了移动平均值,这样可以减少其他因素造成的影响,包括电磁流量计的故障。(当中降噪量等于计算平均值时所考虑的数据量的平方值,即是15的平方根)。我们还可以更快地检测到异常。
相反,正常斜率范围的方法是通过简单标准偏差来计算的,它花费的时间更少,并且可以检测到更多的异常情况,继而发现更多细微的错误,更频繁地提醒人们和防止将来出现严重的漏水问题。
我们将8个区域的数据存储到一个Excel档案中,并使用Python编程检查异常情况,以便计算所需的数字(如移动标准偏差、斜率等)。使用Python程式亦有助我们快速、清晰地检测异常情况,容易找出流水量异常的情况,亦即超出数据正常范围或数据斜率正常范围的日子。
设计数学模型后,我们根据数据测试了模型,亦评估了模型的优势和局限。
这个数学模型的优势之一,就是它能够让人更有效地检测水流的异常情况。当电磁流量计检测到任何水流异常,便可以立即将信号传送到供水系统,提醒及警告人们尽快修理水管或供水系统,从而可以防止漏水问题恶化。
另外,我们的模型非常易于使用。我们只需要下载 Excel档案,并输入区域号码,就可以迅速在数据中找到异常点。这让我们能够在短时间内识别漏水问题,从而进一步提高供水系统的效率和效力。
最后,我们的数学模型能够非常全面地检测水流异常。我们通过两种方法检测异常水流:计算数据的正常范围和数据斜率的正常范围,这既能检测严重的漏水问题,又能找出轻微的漏水现象。
可是,我们的数学模型也有一个局限。由于每个区域的人口众多,在较小的水管分支里,水输入和输出量差异不大,因此我们无法检测到当中异常的水流,也就忽略了较小的水管分支中的漏水问题。
总括而言,我们建立了一个能够同时了解多个流量计的数学模型及有效地检测流量异常的情况,并 (1)分析了数据模式并找出识别数据异常的标准,(2)建立了通用的数学模型,根据数据分析的结果对8个虚拟区域进行了异常水流量的检测,以及 (3)根据数据测试我们建设的数学模型,然后就模型和异常检测的结果做出解释。我们希望透过提醒供水机构和大众关于漏水的情况,防止潜在故障恶化,避免公众面临的严重漏水问题。
参考
- Variance: Simple Definition, Step by Step Examples https://www.statisticshowto.datasciencecentral.com/probability-and-statistics/variance/
- Standard Deviation https://www.statisticshowto.datasciencecentral.com/probability-and-statistics/variance/
- What is R-squared https://www.displayr.com/what-is-r-squared/
- Bell Curve and Normal Distribution Definition https://www.thoughtco.com/bell-curve-normal-distribution-defined-2312350
- Moving Average https://www.investopedia.com/terms/m/movingaverage.asp
- Calculating standard deviation step by step https://www.khanacademy.org/math/statistics-probability/summarizing-quantitative-data/variance-standard-deviation-population/a/calculating-standard-deviation-step-by-step
- Moving Averages and Simple Moving Averages http://www.informit.com/articles/article.aspx?p=2433607&seqNum=2
- Cumulative Moving Average https://qkdb.wordpress.com/2013/05/11/cumulative-moving-average/
- Calculating standard deviation step by step https://www.khanacademy.org/math/statistics-probability/summarizing-quantitative-data/variance-standard-deviation-population/a/calculating-standard-deviation-step-by-step
- Moving Averages and Centered Moving Averages https://www.mathsisfun.com/data/standard-deviation.html
- Standard Deviation and Variance https://www.mathsisfun.com/data/standard-deviation.html
- Bell Curve and Normal Distribution Definition https://www.thoughtco.com/bell-curve-normal-distribution-defined-2312350
- Moving Average Filters https://www.analog.com/media/en/technical-documentation/dsp-book/dsp_book_Ch15.pdf
2020年7月